展开与折叠

课件27张PPT。 这些包装盒漂亮吗？它们是怎样制作的？展开与折叠（一）想一想：
刚才是圆柱和圆锥的侧面展开图.
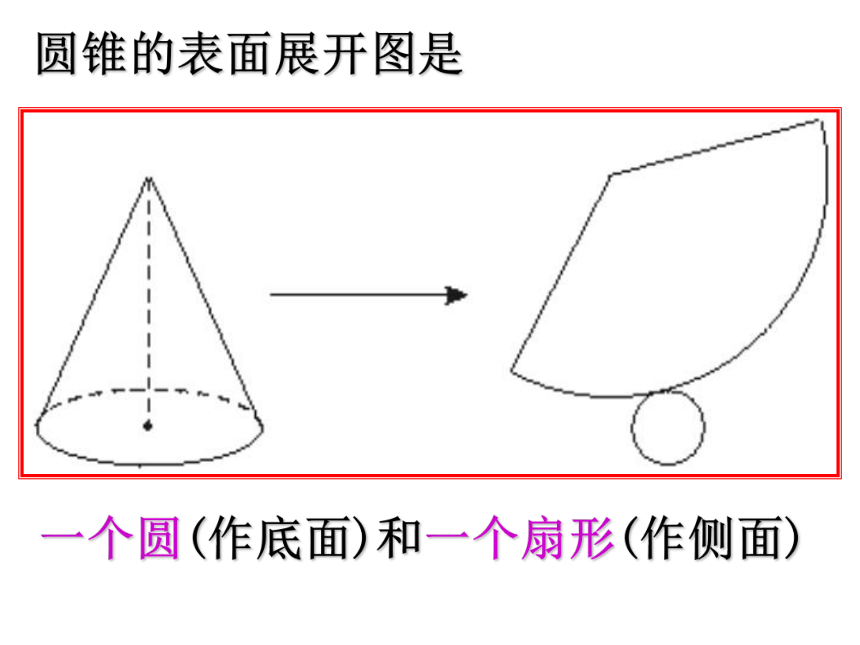
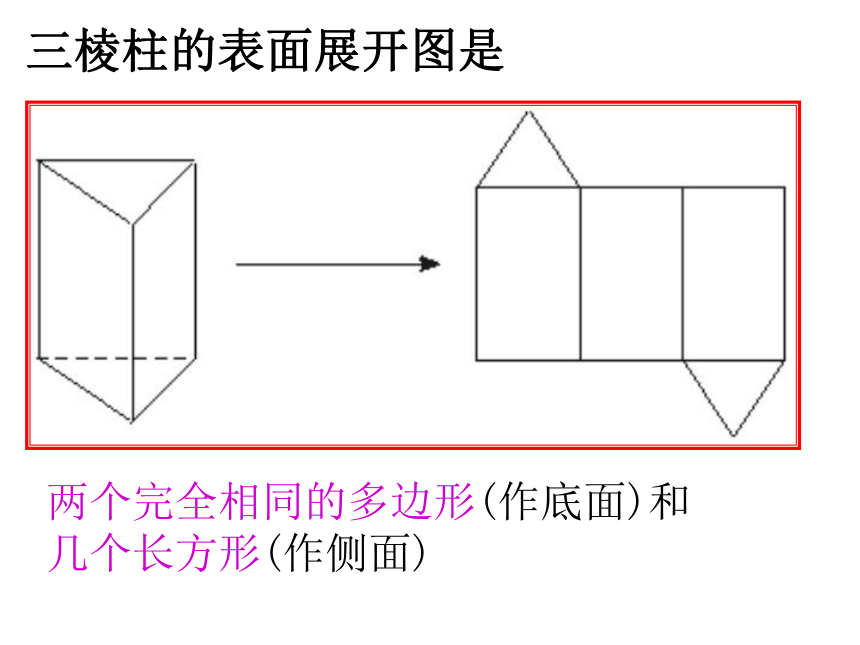
那么圆柱和圆锥的表面展开图是怎样的呢？圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面) 圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面) 三棱柱的表面展开图是两个完全相同的多边形(作底面)和
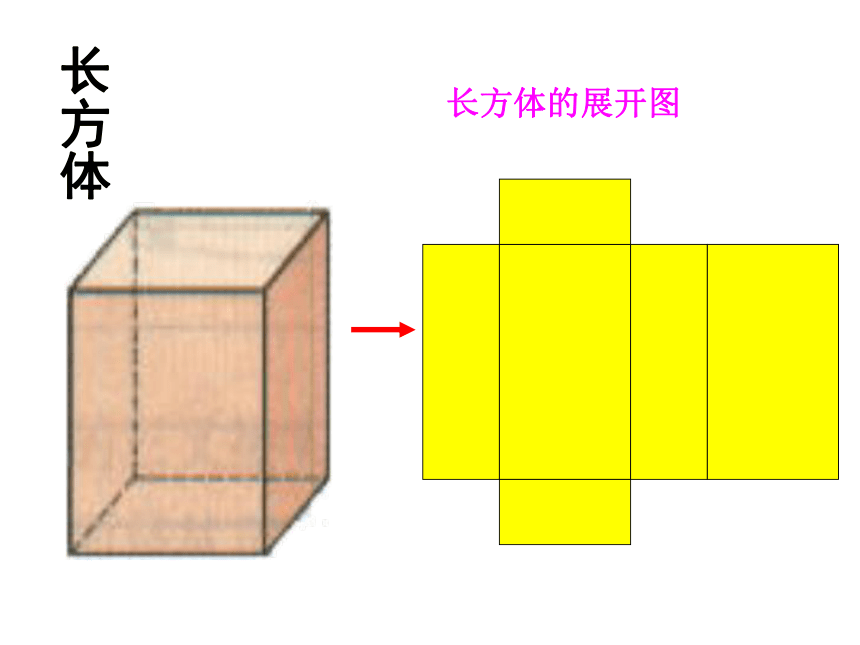
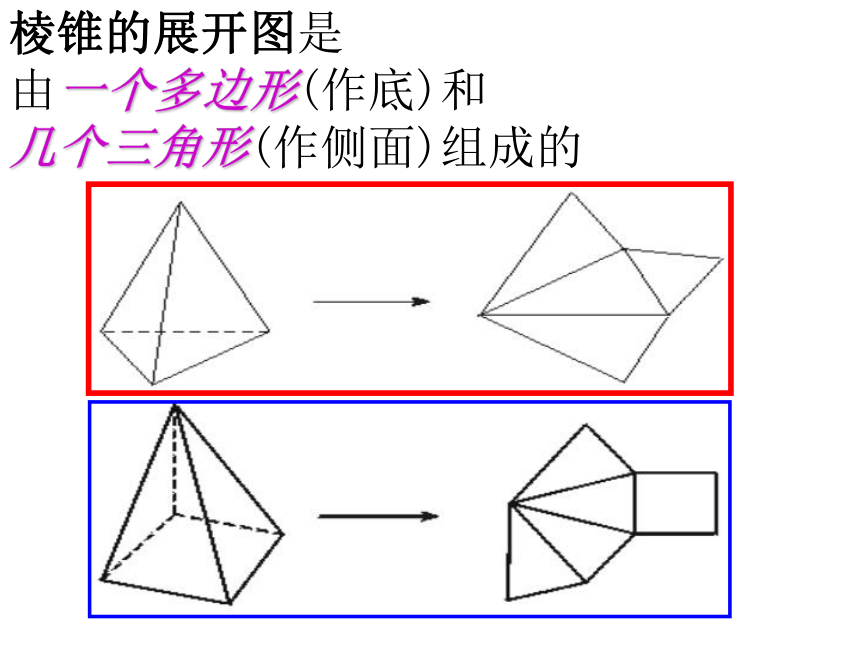
几个长方形(作侧面)长方体长方体的展开图棱锥的展开图是
由一个多边形(作底)和
几个三角形(作侧面)组成的 1、如图，第一行的几何体表面展开后得到的第二行的某个平面图形，请用线连一连。［例］下面图形经过折叠能否围成棱柱？(3)可以折成棱柱 (1)侧面数(4个)≠底面边数(3条)，不能围成棱柱．(2)两底面在侧面展开图的同一端,不在两端,所以也不能
围成棱柱．想一想： 由四个面围成的正方体纸盒，将它展开，得到什么平面图形，请画出它的示意图。解： 一个无盖的正方体纸盒，下底面标有字母A，沿图中的红线将该纸盒剪开，请画出它的示意图。
动动脑： 一个无盖的正方体纸盒，下底面标有字母A，沿图中的红线将该纸盒剪开，请画出它的示意图。
解：动动脑： 如何将一个正方体纸盒沿棱剪开，并展开成一个平面图形？小组合作：思考：
( 1 ).同一个正方形纸盒的表面沿不同的棱剪开，展开成的平面图形是否相同？
（2）把一个正方形纸盒的表面展成一个平面图形，要剪开多少条棱？ 要将一个正方体纸盒的表面展开成一个平面图形，要剪开多少条棱？ 将相对的两个面涂上相同的颜色，正方体的平面展开图共有以下11种：第一类，中间四连方，两侧各一个，共六种。第二类，中间三连方，两侧各有一、二个，共三种。第三类，中间二连方，两侧各有二个，只有一种。第四类，两排各三个，只有一种。 2、如图，哪一个是棱锥侧面展开图？（1）（2）（3）3．下图所示的平面图形中不能围成三棱柱的是( )B4.下列哪个平面图形沿虚线折叠不能围成正方体的是( )B小结本节课你学到了什么?友情提醒：不是所有立体图形都有平面展开图，比如球体。作业：补充习题第一课时。