沪科版2023-2024学年度上学期九年级期末模拟数学试题1(含解析)
文档属性
| 名称 | 沪科版2023-2024学年度上学期九年级期末模拟数学试题1(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 16:48:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版2023-2024九年级上期末模拟试题1
考试范围:九上-九下24.2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
按键的结果为m;
按键的结果为n;
按键的结果为k.
下列判断正确的是( )
A. B. C. D.
下列智能手机的功能图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
如图,直线∥∥,直线AC分别交,,于点A,B,C;直线DF分别交,,于点D,E,F. AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为【 】
A. B. 2 C. D.
如果100N的压力F作用于物体上,产生的压强p要大于1000Pa,则下列关于物体受力面积S(m2)的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2 C.S小于10m2 D.S大于10m2
在同一时刻,物体的高度与它在阳光下的影长成正比.在某一时刻,有人测得一高为的竹竿的影长为,某一高楼的影长为,那么这幢高楼的高度是( )
A. B. C. D.
下列关于图形对称性的命题,正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.正三角形既是轴对称图形,又是中心对称图形
C.线段是轴对称图形,但不是中心对称图形
D.菱形是中心对称图形,但不是轴对称图形
若抛物线与x轴两个交点间的距离为4.对称轴为,P为这条抛物线的顶点,则点P关于x轴的对称点的坐标是( )
A. B. C. D.
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是( )
A.144cm B.180cm C.240cm D.360cm
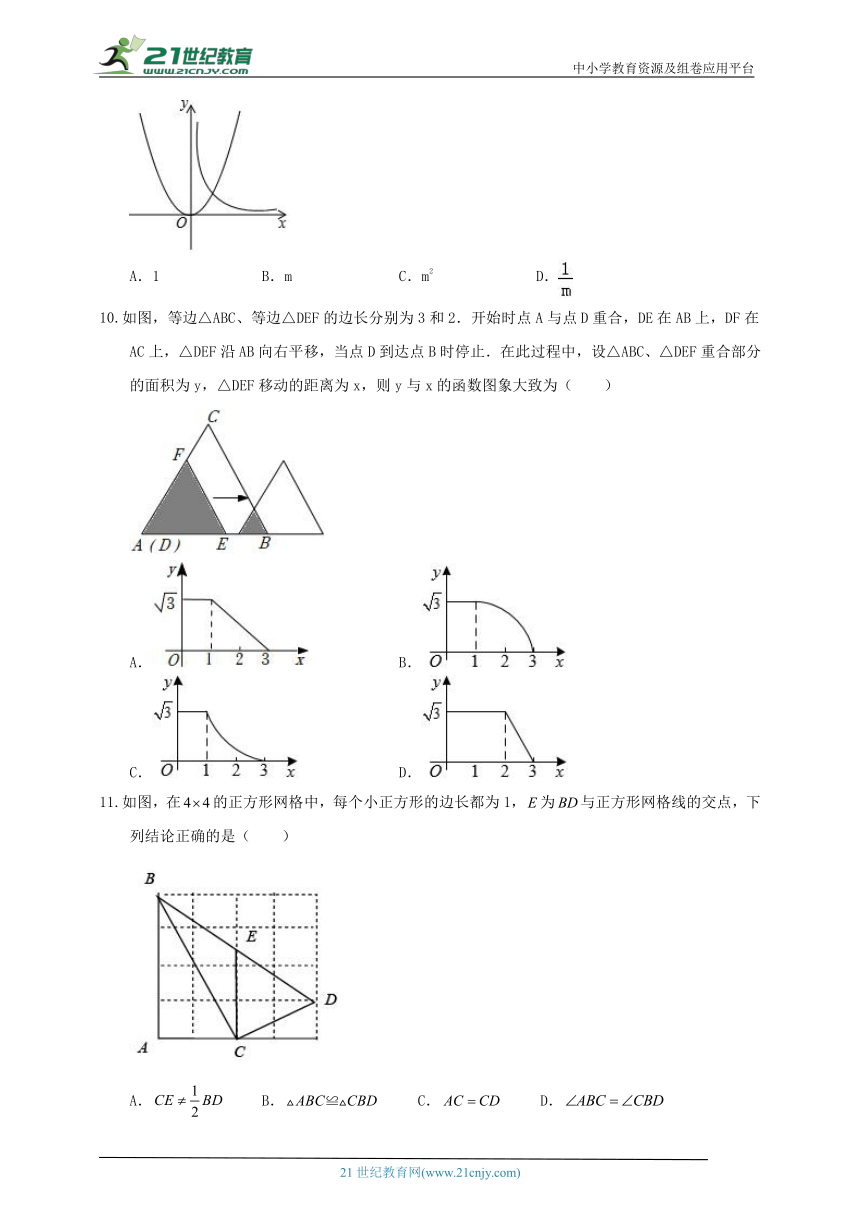
在同一直角坐标系中,二次函数y=x2与反比例函数y=(x>0)的图象如图所示,若两个函数图象上有三个不同的点A(x1,m),B(x2,m),C(x3,m),其中m为常数,令ω=x1+x2+x3,则ω的值为( )
A.1 B.m C.m2 D.
如图,等边△ABC、等边△DEF的边长分别为3和2.开始时点A与点D重合,DE在AB上,DF在AC上,△DEF沿AB向右平移,当点D到达点B时停止.在此过程中,设△ABC、△DEF重合部分的面积为y,△DEF移动的距离为x,则y与x的函数图象大致为( )
A. B.
C. D.
如图,在的正方形网格中,每个小正方形的边长都为1,为与正方形网格线的交点,下列结论正确的是( )
A. B. C. D.
二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,﹣2)的上方,下列结论:①b>0;②2a<b;③2a﹣b﹣1<0;④2a+c<0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
1 、填空题(本大题共6小题,每小题4分,共24分)
二次函数y=x2+3x+n的图象与x轴有一个交点在y轴右侧,则n的值可以是 .(填一个值即可)
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半
轴于点C,则∠BAC等于 度
如图,在平面直角坐标系中,△OAB为直角三角形,∠A=90°,∠AOB=30°,OB=4.若反比例函数y=(k≠0)的图象经过OA的中点C,交AB于点D,则k= .
如图,在矩形ABCD中,AB=8,AD=10,点M为BC的中点,E是BM上的一点,连接AE,作点B关于直线AE的对称点B′,连接DB′并延长交BC于点F.当BF最大时,点B′到BC的距离是 .
如图,点A.B在反比函数的图象上,A.B的纵坐标分别是3和6,连接、,则的面积是__________.
抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1.下列结论中:
①abc>0;
②2a+b=0;
③方程ax2+bx+c=3有两个不相等的实数根;
④抛物线与x轴的另一个交点坐标为(﹣2,0);
⑤若点A(m,n)在该抛物线上,则am2+bm+c≤a+b+c.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
1 、解答题(本大题共8小题,共78分)
计算:4sin60°﹣()﹣1﹣.
如图,已知线段,垂足为a.
(1)求作四边形,使得点B,D分别在射线上,且,,;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设P,Q分别为(1)中四边形的边的中点,求证:直线相交于同一点.
如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.
如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k为常数,k≠0)的图象交于A.B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=,B(m,﹣2).
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出:当y1>y2时,x的取值范围.
如图,在直角梯形ABCD中,,∠DAB=90°,AB=8,CD=5,BC=3.
(1)求梯形ABCD的面积;
(2)联结BD,求∠DBC的正切值.
红星公司销售一种成本为40元/件的产品,若月销售单价不高于50元/件.一个月可售出5万件;月销售单价每涨价1元,月销售量就减少万件.其中月销售单价不低于成本.设月销售单价为x(单位:元/件),月销售量为y(单位:万件).
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.
在平面直角坐标系中,关于的二次函数的图象过点,.
(1)求这个二次函数的表达式;
(2)求当时,的最大值与最小值的差;
(3)一次函数的图象与二次函数的图象交点的横坐标分别是和,且,求的取值范围.
如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
答案解析
1 、选择题
【考点】科学计算器的应用
【分析】根据每一次的按键顺序列出相应的数学算式,得到结果比较即可.
解:第一次按键转换的数学式子为:,即
第二次按键转换的数学式子为: ,即
第三次按键转换的数学式子为: ,即
∴
故选:
【点评】本题考查的是科学计算器的应用,根据按键顺序转换成数学式子,计算即可.
【考点】轴对称图形,中心对称图形
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
解:A.不是轴对称图形,是中心对称图形,故本选项错误,
B、是轴对称图形,不是中心对称图形,故本选项错误,
C、既是轴对称图形,也是中心对称图形,故本选项正确,
D、是轴对称图形,不是中心对称图形,故本选项错误.
故选:C.
【点评】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
【考点】平行线分线段成比例定理
【分析】根据平行线分线段成比例定理得出 ,代入求出即可.
解:∵AG=2,GB=1,BC=5,
∴.
∵直线∥∥,
∴.
故选D.
【点评】本题考查了平行线分线段成比例定理,注意:一组平行线截两条直线,所截的线段对应成比例.
【考点】反比例函数的应用.
【分析】根据已知条件利用压强公式推导即可得到答案.
解:∵,F=100,
∴,
∵产生的压强p要大于1000Pa,
∴,
∴S<0.1,
故选:A.
【点评】本题考查了反比例的应用等知识点,熟练掌握其性质是解决此题的关键.
【考点】相似三角形的应用
【分析】设此高楼的高度为x米,再根据同一时刻物高与影长成正比列出关于x的比例式,求出x的值即可.
解:设这幢高楼的高度为米,依题意得:,
解得:.
故这栋高楼的高度为36米.
故选:.
【点评】本题考查的是相似三角形的应用,熟知同一时刻物高与影长成正比是解答此题的关键.
【考点】命题与定理.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
解:A.圆既是轴对称图形,又是中心对称图形,故A符合题意;
B、正三角形既是轴对称图形,不是中心对称图形,故B不符合题意;
C、线段是轴对称图形,是中心对称图形,故C不符合题意;
D、菱形是中心对称图形,是轴对称图形,故D不符合题意;
故选:A.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
【考点】二次函数的图象与性质,抛物线与x轴的交点
【分析】设抛物线与轴的两个交点坐标分别为,且,根据“两个交点间的距离为4,对称轴为”建立方程可求出的值,再利用待定系数法求出抛物线的解析式,从而可得顶点的坐标,然后根据关于轴的对称点的坐标变换规律即可得.
解:设抛物线与轴的两个交点坐标分别为,且,
由题意得:,解得,
则抛物线与轴的两个交点坐标分别为,
将点代入得:,解得,
则抛物线的解析式为,
顶点的坐标为,
则点关于轴的对称点的坐标是,
故选:A.
【点评】本题考查了二次函数的性质、关于轴的对称点的坐标变换规律,熟练掌握二次函数的性质是解题关键.
【考点】解直角三角形的应用
【分析】根据题意可知:△AEO∽△ABD,从而可求得BD的长,然后根据锐角三角函数的定义可求得AD的长
解:由题平面图如图所示,
根据题意可知:△AFO∽△ACD,OF=EF=30cm
=
∴
∴CD=72cm,
∵tanα=
∴
∴AD==180cm.
故选:B.
【点评】此题考查了三角函数的基本概念,主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.
【考点】反比例函数的图象;反比例函数图象上点的坐标特征;二次函数的图象;二次函数图象上点的坐标特征
【分析】三个点的纵坐标相同,由图象可知y=x2图象上点横坐标互为相反数,则x1+x2+x3=x3,再由反比例函数性质可求x3.
解:设点A.B在二次函数y=x2图象上,点C在反比例函数y=(x>0)的图象上.因为AB两点纵坐标相同,则A.B关于y轴对称,则x1+x2=0,因为点C(x3,m)在反比例函数图象上,则x3=
∴ω=x1+x2+x3=x3=
故选:D.
【点评】本题考查二次函数图象的轴对称性,二次函数图象上点纵坐标相同时,对应点关于抛物线对称轴对称.
【考点】等边三角形的性质,二次函数的性质,动点问题的函数图象
【分析】当△DEF在△ABC内移动时,△ABC、△DEF重合部分的面积不变,当△DEF移出△ABC时,计算出S△DBN,得到,从而得到答案.
解:如图所示,当E和B重合时,AD=AB﹣DB=3﹣2=1,
∴当△DEF移动的距离为0≤x≤1时,△DEF在△ABC内,y=S△DEF==,
当E在B的右边时,如图所示,设移动过程中DF与CB交于点N,过点N坐NM垂直于AE,垂足为M,
根据题意得AD=x,AB=3,
∴DB=AB﹣AD=3﹣x,
∵∠NDB=60°,∠NBD=60°,
∴△NDB是等边三角形,
∴DN=DB=NB=3﹣x,
∵NM⊥DB,
∴,
∵NM2+DM2=DN2,
∴,
∴,
∴,
∴当1≤x≤3时,y是一个关于x的二次函数,且开口向上,
∵当0≤x≤1时,,
故选:C.
【点评】本题考查图形移动、等边三角形的性质,二次函数的性质,根据题意得到二次函数的解析式是解题的关键.
【考点】勾股定理的逆定理,相似三角形的性质与判定,直角三角形斜边上的中线
【分析】由题意易得CE∥AB,然后根据相似三角形的性质与判定、直角三角形斜边中线定理及全等三角形的判定可排除选项.
解:∵每个小正方形的边长都为1,
∴,
∴,,故C错误;
∴△BCD是直角三角形,
∴,
∵,
∴,故B错误;
∴,故D正确;
∵为与正方形网格线的交点,
∴CE∥AB,
∴,
∴,
∴,
∴,故A错误;
故选D.
【点评】本题主要考查勾股定理的逆定理、相似三角形的性质与判定及直角三角形斜边中线定理,熟练掌握勾股定理的逆定理、相似三角形的性质与判定及直角三角形斜边中线定理是解题的关键.
【考点】二次函数图象与系数的关系.
【分析】①由图象开口向上知a>0,由y=ax2+bx+c与x轴的另一个交点坐标为(x1,0 ),且1<x1<2,则该抛物线的对称轴为x=﹣=>﹣,即 <1,于是得到b>0;故①正确;②由x=﹣2时,4a﹣2b+c=0得2a﹣b=﹣,而﹣2<c>0,解不等式即可得到2a>b,所以②错误.③由②知2a﹣b<0,于是得到2a﹣b﹣1<0,故③正确;④把(﹣2,0)代入y=ax2+bx+c得:4a﹣2b+c=0,即2b=4a+c>0(因为b>0),等量代换得到2a+c<0,故④正确.
解:如图:
①由图象开口向上知a>0,
由y=ax2+bx+c与x轴的另一个交点坐标为(x1,0 ),且1<x1<2,
则该抛物线的对称轴为x=﹣=﹣=>﹣,即 <1,
由a>0,两边都乘以a得:b>a,
∵a>0,对称轴x=﹣<0,
∴b>0;故①正确;
②由x=﹣2时,4a﹣2b+c=0得2a﹣b=﹣,而﹣2<c<0,∴2a﹣b>0,所以②错误.
③当x=﹣2时,4a﹣2b+c=0,∴c=﹣4a+2b.∵c>﹣2,
∴﹣4a+2b>﹣2,∴4a﹣2b﹣2<0,
∴2a﹣b﹣1<0,
故③正确;
④∵把(﹣2,0)代入y=ax2+bx+c得:4a﹣2b+c=0,
∴即2b=4a+c>0(因为b>0),
∵当x=1时,a+b+c<0,
∴2a+2b+2c<0,
∴6a+3c<0,
即2a+c<0,∴④正确;
故选C.
【点评】本题考查了二次函数图象与系数的关系,主要考查学生根据图形进行推理和辨析的能力,用了数形结合思想,题目比较好,但是难度偏大.
1 、填空题
【考点】抛物线与x轴的交点,二次函数的性质.
【分析】根据根与系数的关系即可求解.
解:设二次函数y=x2+3x+n的图象与x轴交点的横坐标为x1x2,
即二元一次方程x2+3x+n=0的根为x1x2,
由根与系数的关系得:x1+x2=﹣3,x1 x2=n,
∵一次函数y=x2+3x+n的图象与x轴有一个交点在y轴右侧,
∴x1,x2为异号,
∴n<0,
故答案为:﹣3(答案不唯一).
【点评】本题考查抛物线与x轴的交点,根与系数之间的关系,关键是根与系数之间的关系的应用.
【考点】点与圆的位置关系,锐角三角函数
【分析】解题的关键是正确把握坐标平面内点坐标的意义.
解:由“点A(0,1),B(0,-1)”可得⊙A的半径为2,OA=1,
∴在Rt△AOC中,cos∠BAC=,
∴∠BAC=60°
【点评】本题考查了垂径定理的应用,关键是求出AC、OA的长.
【考点】几何变换综合题.
【分析】先根据直角三角形中30°的角所对的直角边是斜边的一半求出AB,再根据勾股定理求出OA,在Rt△AOE中求出AE,OE,最后根据点C是OA的中点求出点C的坐标,利用待定系数法求出k的值即可.
解:过点A作AE⊥OB于点E,过点C作CF⊥OB于点F,
∵∠A=90°,∠AOB=30°,OB=4,
∴,
由勾股定理得,
在Rt△AOE中,∠AOB=30°,,
∴,
由勾股定理得,
∵点C是OA的中点,
∴,,
∵点C在第一象限,
∴点C的坐标是,
∵反比例函数的图象经过OA的中点C,
∴,
故答案为:.
【点评】本题考查了反比例函数与几何的综合题,熟知直角三角形中30°的角所对的直角边是斜边的一半,熟练掌握勾股定理,求出点C的坐标是此题的关键.
【考点】矩形的性质,轴对称的性质,相似三角形的判定与性质.
【分析】 当DF⊥AB'时,BF有最大值,即点E与点F重合,由勾股定理可求CE的长,可求BE=B'E=4,通过证明△EB'H∽△EDC,即可求解.
解:如图,过点B'作BH⊥BC于H,
∵点B关于直线AE的对称点B′,
∴AB=AB',BE=B'E,∠AEB=∠AEB',∠ABE=∠AB'E,
当DF⊥AB'时,BF有最大值,
∴∠AB'F=∠AB'E=90°,
∴点E与点F重合,
∵AD∥BC,
∴∠DAE=∠AEB=∠AEB',
∴AD=DE=10,
∴CE===6,
∴BE=4=B'E,
∵B'H⊥BC,DC⊥BC,
∴B'H∥CD,
∴△EB'H∽△EDC,
∴,
∴,
∴EB'=,
∴点B′到BC的距离是,
故答案为:.
【点评】本题考查了矩形的性质,轴对称的性质,相似三角形的判定和性质,确定点F的位置是解题的关键.
【考点】反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
【分析】设BD⊥y轴于点D,AC⊥y轴于点C,AC与OB的交点为点E,证得S四边形EBDC=S△AOE即可得S△AOB=S四边形ABDC,根据梯形的面积公式求解即可.
解:如图,设BD⊥y轴于点D,AC⊥y轴于点C,AC与OB的交点为点E,
∵A.B的纵坐标分别是3和6,
代入函数关系式可得横坐标分别为4,2;
∴A(4,3),B(2,6);
∴AC=4,BD=2,CD=3
由反比例函数的几何意义可得S△BOD=S△AOC,
∴S四边形EBDC=S△AOE,
∴S△AOB=S四边形ABDC= ,
故答案为:9.
【点评】本题考查了反比例函数中三角形面积的求解,要能够熟练掌握反比例函数的性质和几何意义;双曲线上任意一点向x轴或y轴引垂线,则该点、垂足、原点组成的三角形的面积相等,都是.
【考点】根的判别式;二次函数图象与系数的关系;二次函数图象上点的坐标特征;抛物线与x轴的交点
【分析】结合函数图象,根据二次函数的性质及二次函数与一元二次方程、一元二次不等式间的关系逐一判断即可.
解:①∵对称轴是y轴的右侧,
∴ab<0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,
故①错误;
②∵﹣=1,
∴b=﹣2a,2a+b=0,
故②正确;
③由图象得:y=3时,与抛物线有两个交点,
∴方程ax2+bx+c=3有两个不相等的实数根;
故③正确;
④∵抛物线与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1,
∴抛物线与x轴的另一个交点坐标为(﹣2,0);
故④正确;
⑤∵抛物线的对称轴是x=1,
∴y有最大值是a+b+c,
∵点A(m,n)在该抛物线上,
∴am2+bm+c≤a+b+c,
故⑤正确;
本题正确的结论有:②③④⑤,4个,
故选:B.
【点评】本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);也考查了抛物线与x轴的交点以及二次函数的性质.
1 、解答题
【分析】依据特殊锐角三角函数值、负整数指数幂的性质、二次根式的性质进行解答即可.
解:原式=4×﹣2﹣2
=2﹣2﹣2
=﹣2.
【点评】本题主要考查的是实数的运算,熟练掌握特殊锐角三角函数值、负整数指数幂的性质、二次根式的性质是解题的关键.
【考点】平行线的性质,等边三角形的性质,作图—复杂作图,平行线分线段成比例
【分析】(1)根据,点B在射线上,过点A作;根据等边三角形性质,得,分别过点A.B,为半径画圆弧,交点即为点C;再根据等边三角形的性质作CD,即可得到答案;
(2)设直线与相交于点S、直线与相交于点,根据平行线和相似三角形的性质,得,从而得,即可完成证明.
解:(1)作图如下:
四边形是所求作的四边形;
(2)设直线与相交于点S,
∵,
∴,
∴
设直线与相交于点,
同理.
∵P,Q分别为的中点,
∴,
∴
∴,
∴,
∴,
∴,
∴点S与重合,即三条直线相交于同一点.
【点评】本题考查了尺规作图、等边三角形、直角三角形、平行线、相似三角形等基础知识,解题的关键是熟练掌握推理能力、空间观念、化归与转化思想,从而完成求解.
【考点】旋转的性质,平移的性质,相似三角形的判定与性质
【分析】(1)由旋转的性质得,AD=AB=10,∠ABD=45°,再由平移的性质即可得出结论;
(2)先判断出∠ADE=∠ACB,进而得出△ADE∽△ACB,得出比例式求出AE,即可得出结论.
解:(1)∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到,
∴∠DAB=90°,AD=AB=10,
∴∠ABD=45°,
∵△EFG是△ABC沿CB方向平移得到,
∴AB∥EF,
∴∠BDF=∠ABD=45°;
(2)由平移的性质得,AE∥CG,AB∥EF,
∴∠DEA=∠DFC=∠ABC,∠ADE+∠DAB=180°,
∵∠DAB=90°,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∴△ADE∽△ACB,
∴,
∵AB=8,AB=AD=10,
∴AE=12.5,
由平移的性质得,CG=AE=12.5.
【点评】此题主要考查了图形的平移与旋转,平行线的性质,等腰直角三角形的判定和性质,解直角三角形,相似三角形的判定和性质,判断出△ADE∽△ACB是解本题的关键。
【考点】反比例函数与一次函数的交点问题
【分析】(1)求得A(2,3),把A(2,3)代入y2=可得反比例函数的解析式为y=,求得B(﹣3,﹣2),把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得一次函数的解析式为y=x+1.
(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.
解:(1)∵OC=2,tan∠AOC=,
∴AC=3,
∴A(2,3),
把A(2,3)代入y2=可得,k=6,
∴反比例函数的解析式为y=,
把B(m,﹣2)代入反比例函数,可得m=﹣3,
∴B(﹣3,﹣2),
把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得
,
解得,
∴一次函数的解析式为y=x+1.
(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.
【点评】本题考查一次函数与反比例函数的交点问题,解题的关键是学会利用待定系数法确定函数解析式,知道两个函数图象的交点坐标可以利用解方程组解决,学会利用图象确定自变量取值范围.
【考点】解直角三角形的应用
【分析】(1)过C作CE⊥AB于E,推出四边形ADCE是矩形,得到AD=CE,AE=CD=5,根据勾股定理得到,即可求出梯形的面积;
(2) 过C作CH⊥BD于H,根据相似三角形的性质得到,根据勾股定理得到,即可求解.
解:(1)过C作CE⊥AB于E,如下图所示:
∵ABDC,∠DAB=90°,∴∠D=90°,
∴∠A=∠D=∠AEC=90°,
∴四边形ADCE是矩形,
∴AD=CE,AE=CD=5,
∴BE=AB﹣AE=3.
∵BC=3,∴CE==6,
∴梯形ABCD的面积=×(5+8)×6=39,
故答案为:39.
(2)过C作CH⊥BD于H,如下图所示:
∵CDAB,∴∠CDB=∠ABD.
∵∠CHD=∠A=90°,
∴△CDH∽△DBA,∴,
∵BD===10,
∴,∴CH=3,
∴BH===6,
∴∠DBC的正切值===.
故答案为:.
【点评】本题考查了直角梯形,解直角三角形,相似三角形的判定和性质,矩形的判定和性质,正确的作出辅助线是解题的关键.
【考点】二次函数的应用,一次函数的应用
【分析】(1)分和两种情况,根据“月销售单价每涨价1元,月销售量就减少万件”即可得函数关系式,再根据求出的取值范围;
(2)在(1)的基础上,根据“月利润(月销售单价成本价)月销售量”建立函数关系式,分别利用一次函数和二次函数的性质求解即可得;
(3)设该产品的捐款当月的月销售利润为万元,先根据捐款当月的月销售单价、月销售最大利润可得,再根据“月利润(月销售单价成本价)月销售量”建立函数关系式,然后利用二次函数的性质即可得.
解:(1)由题意,当时,,
当时,,
,
,
解得,
综上,;
(2)设该产品的月销售利润为万元,
①当时,,
由一次函数的性质可知,在内,随的增大而增大,
则当时,取得最大值,最大值为;
②当时,,
由二次函数的性质可知,当时,取得最大值,最大值为90,
因为,
所以当月销售单价是70元/件时,月销售利润最大,最大利润是90万元;
(3)捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元(大于50万元),
,
设该产品捐款当月的月销售利润为万元,
由题意得:,
整理得:,
,
在内,随的增大而增大,
则当时,取得最大值,最大值为,
因此有,
解得.
【点评】本题考查了二次函数与一次函数的实际应用,正确建立函数关系式是解题关键.
【考点】待定系数法求二次函数解析式,二次函数图象的性质,根与系数的关系
【分析】(1)利用待定系数法将点,代入解析式中解方程组即可;
(2)根据(1)中函数关系式得到对称轴,从而知在中,当x=-2时,y有最大值,当时,y有最小值,求之相减即可;
(3)根据两函数相交可得出x与m的函数关系式,根据有两个交点可得出>0,根据根与系数的关系可得出a,b的值,然后根据,整理得出m的取值范围.
解:(1)∵的图象过点,,
∴
解得
∴
(2)由(1)得,二次函数对称轴为
∴当时,y的最大值为(-2)2-(-2)-2=4,
y的最小值为
∴的最大值与最小值的差为;
(3)由题意及(1)得
整理得
即
∵一次函数的图象与二次函数的图象交点的横坐标分别是和,
∴
化简得
即
解得m≠5
∴a,b为方程的两个解
又∵
∴a=-1,b=4-m
即4-m>3
∴m<1
综上所述,m的取值范围为.
【点评】本题考查了利用待定系数法求二次函数解析式,二次函数图象的性质,根与系数的关系等知识.解题的关键是熟记二次函数图象的性质.
【考点】四边形综合题.
【分析】(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG,接下来在证明∠GAE=∠FAE,然后依据SAS证明△GAE≌△FAE即可;②由全等三角形的性质可知:AB=AH,GE=EF=5.设正方形的边长为x,接下来,在Rt△EFC中,依据勾股定理列方程求解即可;
(2)将△ABM逆时针旋转90°得△ADM′.在△NM′D中依据勾股定理可证明NM′2=ND2+DM′2,接下来证明△AMN≌△ANM′,于的得到MN=NM′,最后再由BM=DM′证明即可.
解:(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中,
∴△GAE≌△FAE.
②∵△GAE≌△FAE,AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x﹣2,FC=x﹣3.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,即(x﹣2)2+(x﹣3)2=25.
解得:x=6.
∴AB=6.
∴AH=6.
(3)如图所示:将△ABM逆时针旋转90°得△ADM′.
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,,
∴△AMN≌△ANM′.
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
【点评】 本题主要考查的是四边形的综合应用,解答本题主要应用了旋转的性质、全等三角形的性质和判定、勾股定理的应用,正方形的性质,依据旋转的性质构造全等三角形和直角三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版2023-2024九年级上期末模拟试题1
考试范围:九上-九下24.2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
按键的结果为m;
按键的结果为n;
按键的结果为k.
下列判断正确的是( )
A. B. C. D.
下列智能手机的功能图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
如图,直线∥∥,直线AC分别交,,于点A,B,C;直线DF分别交,,于点D,E,F. AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为【 】
A. B. 2 C. D.
如果100N的压力F作用于物体上,产生的压强p要大于1000Pa,则下列关于物体受力面积S(m2)的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2 C.S小于10m2 D.S大于10m2
在同一时刻,物体的高度与它在阳光下的影长成正比.在某一时刻,有人测得一高为的竹竿的影长为,某一高楼的影长为,那么这幢高楼的高度是( )
A. B. C. D.
下列关于图形对称性的命题,正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.正三角形既是轴对称图形,又是中心对称图形
C.线段是轴对称图形,但不是中心对称图形
D.菱形是中心对称图形,但不是轴对称图形
若抛物线与x轴两个交点间的距离为4.对称轴为,P为这条抛物线的顶点,则点P关于x轴的对称点的坐标是( )
A. B. C. D.
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是( )
A.144cm B.180cm C.240cm D.360cm
在同一直角坐标系中,二次函数y=x2与反比例函数y=(x>0)的图象如图所示,若两个函数图象上有三个不同的点A(x1,m),B(x2,m),C(x3,m),其中m为常数,令ω=x1+x2+x3,则ω的值为( )
A.1 B.m C.m2 D.
如图,等边△ABC、等边△DEF的边长分别为3和2.开始时点A与点D重合,DE在AB上,DF在AC上,△DEF沿AB向右平移,当点D到达点B时停止.在此过程中,设△ABC、△DEF重合部分的面积为y,△DEF移动的距离为x,则y与x的函数图象大致为( )
A. B.
C. D.
如图,在的正方形网格中,每个小正方形的边长都为1,为与正方形网格线的交点,下列结论正确的是( )
A. B. C. D.
二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣2,0),(x0,0),1<x0<2,与y轴的负半轴相交,且交点在(0,﹣2)的上方,下列结论:①b>0;②2a<b;③2a﹣b﹣1<0;④2a+c<0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
1 、填空题(本大题共6小题,每小题4分,共24分)
二次函数y=x2+3x+n的图象与x轴有一个交点在y轴右侧,则n的值可以是 .(填一个值即可)
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半
轴于点C,则∠BAC等于 度
如图,在平面直角坐标系中,△OAB为直角三角形,∠A=90°,∠AOB=30°,OB=4.若反比例函数y=(k≠0)的图象经过OA的中点C,交AB于点D,则k= .
如图,在矩形ABCD中,AB=8,AD=10,点M为BC的中点,E是BM上的一点,连接AE,作点B关于直线AE的对称点B′,连接DB′并延长交BC于点F.当BF最大时,点B′到BC的距离是 .
如图,点A.B在反比函数的图象上,A.B的纵坐标分别是3和6,连接、,则的面积是__________.
抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1.下列结论中:
①abc>0;
②2a+b=0;
③方程ax2+bx+c=3有两个不相等的实数根;
④抛物线与x轴的另一个交点坐标为(﹣2,0);
⑤若点A(m,n)在该抛物线上,则am2+bm+c≤a+b+c.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
1 、解答题(本大题共8小题,共78分)
计算:4sin60°﹣()﹣1﹣.
如图,已知线段,垂足为a.
(1)求作四边形,使得点B,D分别在射线上,且,,;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设P,Q分别为(1)中四边形的边的中点,求证:直线相交于同一点.
如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.
如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k为常数,k≠0)的图象交于A.B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=,B(m,﹣2).
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出:当y1>y2时,x的取值范围.
如图,在直角梯形ABCD中,,∠DAB=90°,AB=8,CD=5,BC=3.
(1)求梯形ABCD的面积;
(2)联结BD,求∠DBC的正切值.
红星公司销售一种成本为40元/件的产品,若月销售单价不高于50元/件.一个月可售出5万件;月销售单价每涨价1元,月销售量就减少万件.其中月销售单价不低于成本.设月销售单价为x(单位:元/件),月销售量为y(单位:万件).
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.
在平面直角坐标系中,关于的二次函数的图象过点,.
(1)求这个二次函数的表达式;
(2)求当时,的最大值与最小值的差;
(3)一次函数的图象与二次函数的图象交点的横坐标分别是和,且,求的取值范围.
如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
答案解析
1 、选择题
【考点】科学计算器的应用
【分析】根据每一次的按键顺序列出相应的数学算式,得到结果比较即可.
解:第一次按键转换的数学式子为:,即
第二次按键转换的数学式子为: ,即
第三次按键转换的数学式子为: ,即
∴
故选:
【点评】本题考查的是科学计算器的应用,根据按键顺序转换成数学式子,计算即可.
【考点】轴对称图形,中心对称图形
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
解:A.不是轴对称图形,是中心对称图形,故本选项错误,
B、是轴对称图形,不是中心对称图形,故本选项错误,
C、既是轴对称图形,也是中心对称图形,故本选项正确,
D、是轴对称图形,不是中心对称图形,故本选项错误.
故选:C.
【点评】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
【考点】平行线分线段成比例定理
【分析】根据平行线分线段成比例定理得出 ,代入求出即可.
解:∵AG=2,GB=1,BC=5,
∴.
∵直线∥∥,
∴.
故选D.
【点评】本题考查了平行线分线段成比例定理,注意:一组平行线截两条直线,所截的线段对应成比例.
【考点】反比例函数的应用.
【分析】根据已知条件利用压强公式推导即可得到答案.
解:∵,F=100,
∴,
∵产生的压强p要大于1000Pa,
∴,
∴S<0.1,
故选:A.
【点评】本题考查了反比例的应用等知识点,熟练掌握其性质是解决此题的关键.
【考点】相似三角形的应用
【分析】设此高楼的高度为x米,再根据同一时刻物高与影长成正比列出关于x的比例式,求出x的值即可.
解:设这幢高楼的高度为米,依题意得:,
解得:.
故这栋高楼的高度为36米.
故选:.
【点评】本题考查的是相似三角形的应用,熟知同一时刻物高与影长成正比是解答此题的关键.
【考点】命题与定理.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
解:A.圆既是轴对称图形,又是中心对称图形,故A符合题意;
B、正三角形既是轴对称图形,不是中心对称图形,故B不符合题意;
C、线段是轴对称图形,是中心对称图形,故C不符合题意;
D、菱形是中心对称图形,是轴对称图形,故D不符合题意;
故选:A.
【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
【考点】二次函数的图象与性质,抛物线与x轴的交点
【分析】设抛物线与轴的两个交点坐标分别为,且,根据“两个交点间的距离为4,对称轴为”建立方程可求出的值,再利用待定系数法求出抛物线的解析式,从而可得顶点的坐标,然后根据关于轴的对称点的坐标变换规律即可得.
解:设抛物线与轴的两个交点坐标分别为,且,
由题意得:,解得,
则抛物线与轴的两个交点坐标分别为,
将点代入得:,解得,
则抛物线的解析式为,
顶点的坐标为,
则点关于轴的对称点的坐标是,
故选:A.
【点评】本题考查了二次函数的性质、关于轴的对称点的坐标变换规律,熟练掌握二次函数的性质是解题关键.
【考点】解直角三角形的应用
【分析】根据题意可知:△AEO∽△ABD,从而可求得BD的长,然后根据锐角三角函数的定义可求得AD的长
解:由题平面图如图所示,
根据题意可知:△AFO∽△ACD,OF=EF=30cm
=
∴
∴CD=72cm,
∵tanα=
∴
∴AD==180cm.
故选:B.
【点评】此题考查了三角函数的基本概念,主要是余弦概念及运算,关键把实际问题转化为数学问题加以计算.
【考点】反比例函数的图象;反比例函数图象上点的坐标特征;二次函数的图象;二次函数图象上点的坐标特征
【分析】三个点的纵坐标相同,由图象可知y=x2图象上点横坐标互为相反数,则x1+x2+x3=x3,再由反比例函数性质可求x3.
解:设点A.B在二次函数y=x2图象上,点C在反比例函数y=(x>0)的图象上.因为AB两点纵坐标相同,则A.B关于y轴对称,则x1+x2=0,因为点C(x3,m)在反比例函数图象上,则x3=
∴ω=x1+x2+x3=x3=
故选:D.
【点评】本题考查二次函数图象的轴对称性,二次函数图象上点纵坐标相同时,对应点关于抛物线对称轴对称.
【考点】等边三角形的性质,二次函数的性质,动点问题的函数图象
【分析】当△DEF在△ABC内移动时,△ABC、△DEF重合部分的面积不变,当△DEF移出△ABC时,计算出S△DBN,得到,从而得到答案.
解:如图所示,当E和B重合时,AD=AB﹣DB=3﹣2=1,
∴当△DEF移动的距离为0≤x≤1时,△DEF在△ABC内,y=S△DEF==,
当E在B的右边时,如图所示,设移动过程中DF与CB交于点N,过点N坐NM垂直于AE,垂足为M,
根据题意得AD=x,AB=3,
∴DB=AB﹣AD=3﹣x,
∵∠NDB=60°,∠NBD=60°,
∴△NDB是等边三角形,
∴DN=DB=NB=3﹣x,
∵NM⊥DB,
∴,
∵NM2+DM2=DN2,
∴,
∴,
∴,
∴当1≤x≤3时,y是一个关于x的二次函数,且开口向上,
∵当0≤x≤1时,,
故选:C.
【点评】本题考查图形移动、等边三角形的性质,二次函数的性质,根据题意得到二次函数的解析式是解题的关键.
【考点】勾股定理的逆定理,相似三角形的性质与判定,直角三角形斜边上的中线
【分析】由题意易得CE∥AB,然后根据相似三角形的性质与判定、直角三角形斜边中线定理及全等三角形的判定可排除选项.
解:∵每个小正方形的边长都为1,
∴,
∴,,故C错误;
∴△BCD是直角三角形,
∴,
∵,
∴,故B错误;
∴,故D正确;
∵为与正方形网格线的交点,
∴CE∥AB,
∴,
∴,
∴,
∴,故A错误;
故选D.
【点评】本题主要考查勾股定理的逆定理、相似三角形的性质与判定及直角三角形斜边中线定理,熟练掌握勾股定理的逆定理、相似三角形的性质与判定及直角三角形斜边中线定理是解题的关键.
【考点】二次函数图象与系数的关系.
【分析】①由图象开口向上知a>0,由y=ax2+bx+c与x轴的另一个交点坐标为(x1,0 ),且1<x1<2,则该抛物线的对称轴为x=﹣=>﹣,即 <1,于是得到b>0;故①正确;②由x=﹣2时,4a﹣2b+c=0得2a﹣b=﹣,而﹣2<c>0,解不等式即可得到2a>b,所以②错误.③由②知2a﹣b<0,于是得到2a﹣b﹣1<0,故③正确;④把(﹣2,0)代入y=ax2+bx+c得:4a﹣2b+c=0,即2b=4a+c>0(因为b>0),等量代换得到2a+c<0,故④正确.
解:如图:
①由图象开口向上知a>0,
由y=ax2+bx+c与x轴的另一个交点坐标为(x1,0 ),且1<x1<2,
则该抛物线的对称轴为x=﹣=﹣=>﹣,即 <1,
由a>0,两边都乘以a得:b>a,
∵a>0,对称轴x=﹣<0,
∴b>0;故①正确;
②由x=﹣2时,4a﹣2b+c=0得2a﹣b=﹣,而﹣2<c<0,∴2a﹣b>0,所以②错误.
③当x=﹣2时,4a﹣2b+c=0,∴c=﹣4a+2b.∵c>﹣2,
∴﹣4a+2b>﹣2,∴4a﹣2b﹣2<0,
∴2a﹣b﹣1<0,
故③正确;
④∵把(﹣2,0)代入y=ax2+bx+c得:4a﹣2b+c=0,
∴即2b=4a+c>0(因为b>0),
∵当x=1时,a+b+c<0,
∴2a+2b+2c<0,
∴6a+3c<0,
即2a+c<0,∴④正确;
故选C.
【点评】本题考查了二次函数图象与系数的关系,主要考查学生根据图形进行推理和辨析的能力,用了数形结合思想,题目比较好,但是难度偏大.
1 、填空题
【考点】抛物线与x轴的交点,二次函数的性质.
【分析】根据根与系数的关系即可求解.
解:设二次函数y=x2+3x+n的图象与x轴交点的横坐标为x1x2,
即二元一次方程x2+3x+n=0的根为x1x2,
由根与系数的关系得:x1+x2=﹣3,x1 x2=n,
∵一次函数y=x2+3x+n的图象与x轴有一个交点在y轴右侧,
∴x1,x2为异号,
∴n<0,
故答案为:﹣3(答案不唯一).
【点评】本题考查抛物线与x轴的交点,根与系数之间的关系,关键是根与系数之间的关系的应用.
【考点】点与圆的位置关系,锐角三角函数
【分析】解题的关键是正确把握坐标平面内点坐标的意义.
解:由“点A(0,1),B(0,-1)”可得⊙A的半径为2,OA=1,
∴在Rt△AOC中,cos∠BAC=,
∴∠BAC=60°
【点评】本题考查了垂径定理的应用,关键是求出AC、OA的长.
【考点】几何变换综合题.
【分析】先根据直角三角形中30°的角所对的直角边是斜边的一半求出AB,再根据勾股定理求出OA,在Rt△AOE中求出AE,OE,最后根据点C是OA的中点求出点C的坐标,利用待定系数法求出k的值即可.
解:过点A作AE⊥OB于点E,过点C作CF⊥OB于点F,
∵∠A=90°,∠AOB=30°,OB=4,
∴,
由勾股定理得,
在Rt△AOE中,∠AOB=30°,,
∴,
由勾股定理得,
∵点C是OA的中点,
∴,,
∵点C在第一象限,
∴点C的坐标是,
∵反比例函数的图象经过OA的中点C,
∴,
故答案为:.
【点评】本题考查了反比例函数与几何的综合题,熟知直角三角形中30°的角所对的直角边是斜边的一半,熟练掌握勾股定理,求出点C的坐标是此题的关键.
【考点】矩形的性质,轴对称的性质,相似三角形的判定与性质.
【分析】 当DF⊥AB'时,BF有最大值,即点E与点F重合,由勾股定理可求CE的长,可求BE=B'E=4,通过证明△EB'H∽△EDC,即可求解.
解:如图,过点B'作BH⊥BC于H,
∵点B关于直线AE的对称点B′,
∴AB=AB',BE=B'E,∠AEB=∠AEB',∠ABE=∠AB'E,
当DF⊥AB'时,BF有最大值,
∴∠AB'F=∠AB'E=90°,
∴点E与点F重合,
∵AD∥BC,
∴∠DAE=∠AEB=∠AEB',
∴AD=DE=10,
∴CE===6,
∴BE=4=B'E,
∵B'H⊥BC,DC⊥BC,
∴B'H∥CD,
∴△EB'H∽△EDC,
∴,
∴,
∴EB'=,
∴点B′到BC的距离是,
故答案为:.
【点评】本题考查了矩形的性质,轴对称的性质,相似三角形的判定和性质,确定点F的位置是解题的关键.
【考点】反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
【分析】设BD⊥y轴于点D,AC⊥y轴于点C,AC与OB的交点为点E,证得S四边形EBDC=S△AOE即可得S△AOB=S四边形ABDC,根据梯形的面积公式求解即可.
解:如图,设BD⊥y轴于点D,AC⊥y轴于点C,AC与OB的交点为点E,
∵A.B的纵坐标分别是3和6,
代入函数关系式可得横坐标分别为4,2;
∴A(4,3),B(2,6);
∴AC=4,BD=2,CD=3
由反比例函数的几何意义可得S△BOD=S△AOC,
∴S四边形EBDC=S△AOE,
∴S△AOB=S四边形ABDC= ,
故答案为:9.
【点评】本题考查了反比例函数中三角形面积的求解,要能够熟练掌握反比例函数的性质和几何意义;双曲线上任意一点向x轴或y轴引垂线,则该点、垂足、原点组成的三角形的面积相等,都是.
【考点】根的判别式;二次函数图象与系数的关系;二次函数图象上点的坐标特征;抛物线与x轴的交点
【分析】结合函数图象,根据二次函数的性质及二次函数与一元二次方程、一元二次不等式间的关系逐一判断即可.
解:①∵对称轴是y轴的右侧,
∴ab<0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,
故①错误;
②∵﹣=1,
∴b=﹣2a,2a+b=0,
故②正确;
③由图象得:y=3时,与抛物线有两个交点,
∴方程ax2+bx+c=3有两个不相等的实数根;
故③正确;
④∵抛物线与x轴的一个交点坐标为(4,0),抛物线的对称轴是x=1,
∴抛物线与x轴的另一个交点坐标为(﹣2,0);
故④正确;
⑤∵抛物线的对称轴是x=1,
∴y有最大值是a+b+c,
∵点A(m,n)在该抛物线上,
∴am2+bm+c≤a+b+c,
故⑤正确;
本题正确的结论有:②③④⑤,4个,
故选:B.
【点评】本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);也考查了抛物线与x轴的交点以及二次函数的性质.
1 、解答题
【分析】依据特殊锐角三角函数值、负整数指数幂的性质、二次根式的性质进行解答即可.
解:原式=4×﹣2﹣2
=2﹣2﹣2
=﹣2.
【点评】本题主要考查的是实数的运算,熟练掌握特殊锐角三角函数值、负整数指数幂的性质、二次根式的性质是解题的关键.
【考点】平行线的性质,等边三角形的性质,作图—复杂作图,平行线分线段成比例
【分析】(1)根据,点B在射线上,过点A作;根据等边三角形性质,得,分别过点A.B,为半径画圆弧,交点即为点C;再根据等边三角形的性质作CD,即可得到答案;
(2)设直线与相交于点S、直线与相交于点,根据平行线和相似三角形的性质,得,从而得,即可完成证明.
解:(1)作图如下:
四边形是所求作的四边形;
(2)设直线与相交于点S,
∵,
∴,
∴
设直线与相交于点,
同理.
∵P,Q分别为的中点,
∴,
∴
∴,
∴,
∴,
∴,
∴点S与重合,即三条直线相交于同一点.
【点评】本题考查了尺规作图、等边三角形、直角三角形、平行线、相似三角形等基础知识,解题的关键是熟练掌握推理能力、空间观念、化归与转化思想,从而完成求解.
【考点】旋转的性质,平移的性质,相似三角形的判定与性质
【分析】(1)由旋转的性质得,AD=AB=10,∠ABD=45°,再由平移的性质即可得出结论;
(2)先判断出∠ADE=∠ACB,进而得出△ADE∽△ACB,得出比例式求出AE,即可得出结论.
解:(1)∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到,
∴∠DAB=90°,AD=AB=10,
∴∠ABD=45°,
∵△EFG是△ABC沿CB方向平移得到,
∴AB∥EF,
∴∠BDF=∠ABD=45°;
(2)由平移的性质得,AE∥CG,AB∥EF,
∴∠DEA=∠DFC=∠ABC,∠ADE+∠DAB=180°,
∵∠DAB=90°,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∴△ADE∽△ACB,
∴,
∵AB=8,AB=AD=10,
∴AE=12.5,
由平移的性质得,CG=AE=12.5.
【点评】此题主要考查了图形的平移与旋转,平行线的性质,等腰直角三角形的判定和性质,解直角三角形,相似三角形的判定和性质,判断出△ADE∽△ACB是解本题的关键。
【考点】反比例函数与一次函数的交点问题
【分析】(1)求得A(2,3),把A(2,3)代入y2=可得反比例函数的解析式为y=,求得B(﹣3,﹣2),把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得一次函数的解析式为y=x+1.
(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.
解:(1)∵OC=2,tan∠AOC=,
∴AC=3,
∴A(2,3),
把A(2,3)代入y2=可得,k=6,
∴反比例函数的解析式为y=,
把B(m,﹣2)代入反比例函数,可得m=﹣3,
∴B(﹣3,﹣2),
把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得
,
解得,
∴一次函数的解析式为y=x+1.
(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.
【点评】本题考查一次函数与反比例函数的交点问题,解题的关键是学会利用待定系数法确定函数解析式,知道两个函数图象的交点坐标可以利用解方程组解决,学会利用图象确定自变量取值范围.
【考点】解直角三角形的应用
【分析】(1)过C作CE⊥AB于E,推出四边形ADCE是矩形,得到AD=CE,AE=CD=5,根据勾股定理得到,即可求出梯形的面积;
(2) 过C作CH⊥BD于H,根据相似三角形的性质得到,根据勾股定理得到,即可求解.
解:(1)过C作CE⊥AB于E,如下图所示:
∵ABDC,∠DAB=90°,∴∠D=90°,
∴∠A=∠D=∠AEC=90°,
∴四边形ADCE是矩形,
∴AD=CE,AE=CD=5,
∴BE=AB﹣AE=3.
∵BC=3,∴CE==6,
∴梯形ABCD的面积=×(5+8)×6=39,
故答案为:39.
(2)过C作CH⊥BD于H,如下图所示:
∵CDAB,∴∠CDB=∠ABD.
∵∠CHD=∠A=90°,
∴△CDH∽△DBA,∴,
∵BD===10,
∴,∴CH=3,
∴BH===6,
∴∠DBC的正切值===.
故答案为:.
【点评】本题考查了直角梯形,解直角三角形,相似三角形的判定和性质,矩形的判定和性质,正确的作出辅助线是解题的关键.
【考点】二次函数的应用,一次函数的应用
【分析】(1)分和两种情况,根据“月销售单价每涨价1元,月销售量就减少万件”即可得函数关系式,再根据求出的取值范围;
(2)在(1)的基础上,根据“月利润(月销售单价成本价)月销售量”建立函数关系式,分别利用一次函数和二次函数的性质求解即可得;
(3)设该产品的捐款当月的月销售利润为万元,先根据捐款当月的月销售单价、月销售最大利润可得,再根据“月利润(月销售单价成本价)月销售量”建立函数关系式,然后利用二次函数的性质即可得.
解:(1)由题意,当时,,
当时,,
,
,
解得,
综上,;
(2)设该产品的月销售利润为万元,
①当时,,
由一次函数的性质可知,在内,随的增大而增大,
则当时,取得最大值,最大值为;
②当时,,
由二次函数的性质可知,当时,取得最大值,最大值为90,
因为,
所以当月销售单价是70元/件时,月销售利润最大,最大利润是90万元;
(3)捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元(大于50万元),
,
设该产品捐款当月的月销售利润为万元,
由题意得:,
整理得:,
,
在内,随的增大而增大,
则当时,取得最大值,最大值为,
因此有,
解得.
【点评】本题考查了二次函数与一次函数的实际应用,正确建立函数关系式是解题关键.
【考点】待定系数法求二次函数解析式,二次函数图象的性质,根与系数的关系
【分析】(1)利用待定系数法将点,代入解析式中解方程组即可;
(2)根据(1)中函数关系式得到对称轴,从而知在中,当x=-2时,y有最大值,当时,y有最小值,求之相减即可;
(3)根据两函数相交可得出x与m的函数关系式,根据有两个交点可得出>0,根据根与系数的关系可得出a,b的值,然后根据,整理得出m的取值范围.
解:(1)∵的图象过点,,
∴
解得
∴
(2)由(1)得,二次函数对称轴为
∴当时,y的最大值为(-2)2-(-2)-2=4,
y的最小值为
∴的最大值与最小值的差为;
(3)由题意及(1)得
整理得
即
∵一次函数的图象与二次函数的图象交点的横坐标分别是和,
∴
化简得
即
解得m≠5
∴a,b为方程的两个解
又∵
∴a=-1,b=4-m
即4-m>3
∴m<1
综上所述,m的取值范围为.
【点评】本题考查了利用待定系数法求二次函数解析式,二次函数图象的性质,根与系数的关系等知识.解题的关键是熟记二次函数图象的性质.
【考点】四边形综合题.
【分析】(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG,接下来在证明∠GAE=∠FAE,然后依据SAS证明△GAE≌△FAE即可;②由全等三角形的性质可知:AB=AH,GE=EF=5.设正方形的边长为x,接下来,在Rt△EFC中,依据勾股定理列方程求解即可;
(2)将△ABM逆时针旋转90°得△ADM′.在△NM′D中依据勾股定理可证明NM′2=ND2+DM′2,接下来证明△AMN≌△ANM′,于的得到MN=NM′,最后再由BM=DM′证明即可.
解:(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中,
∴△GAE≌△FAE.
②∵△GAE≌△FAE,AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x﹣2,FC=x﹣3.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,即(x﹣2)2+(x﹣3)2=25.
解得:x=6.
∴AB=6.
∴AH=6.
(3)如图所示:将△ABM逆时针旋转90°得△ADM′.
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,,
∴△AMN≌△ANM′.
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
【点评】 本题主要考查的是四边形的综合应用,解答本题主要应用了旋转的性质、全等三角形的性质和判定、勾股定理的应用,正方形的性质,依据旋转的性质构造全等三角形和直角三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
