沪科版2023-2024学年度上学期九年级期末模拟数学试题3(含解析)
文档属性
| 名称 | 沪科版2023-2024学年度上学期九年级期末模拟数学试题3(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 16:49:37 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版2023-2024九年级上期末模拟试题3
考试范围:九上-九下24.2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
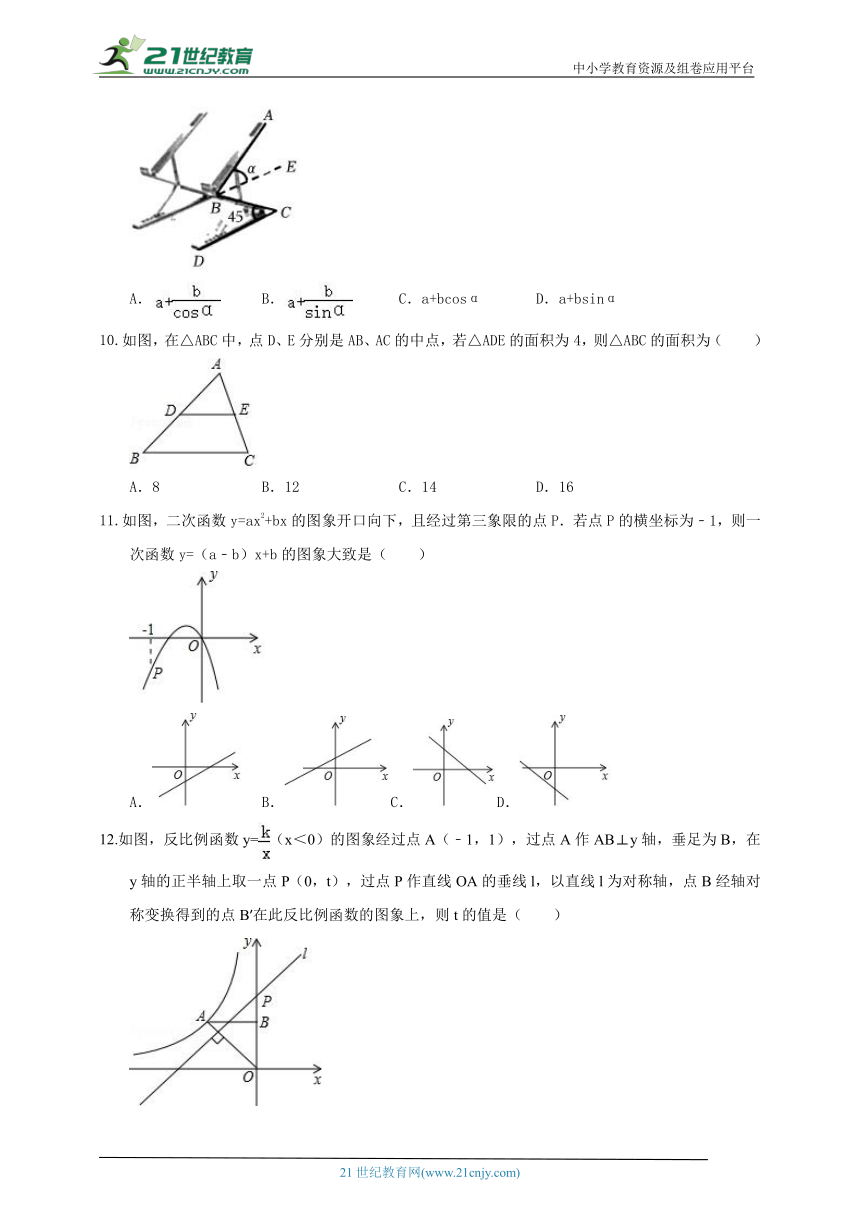
下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
如图,在中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了( )
A.黄金分割数 B.平均数 C.众数 D.中位数
抛物线y=2(x+9)2﹣3的顶点坐标是( )
A.(9,﹣3) B.(﹣9,﹣3) C.(9,3) D.(﹣9,3)
图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B. C. D.
如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m B.24m C.30m D.60m
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x ﹣2 ﹣1 0 1
y 0 4 6 6
下列结论不正确的是( )
A.抛物线的开口向下
B.抛物线的对称轴为直线x=
C.抛物线与x轴的一个交点坐标为(2,0)
D.函数y=ax2+bx+c的最大值为
如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
A.﹣3<x<2
B.x<﹣3或x>2
C.﹣3<x<0或x>2
D.0<x<2
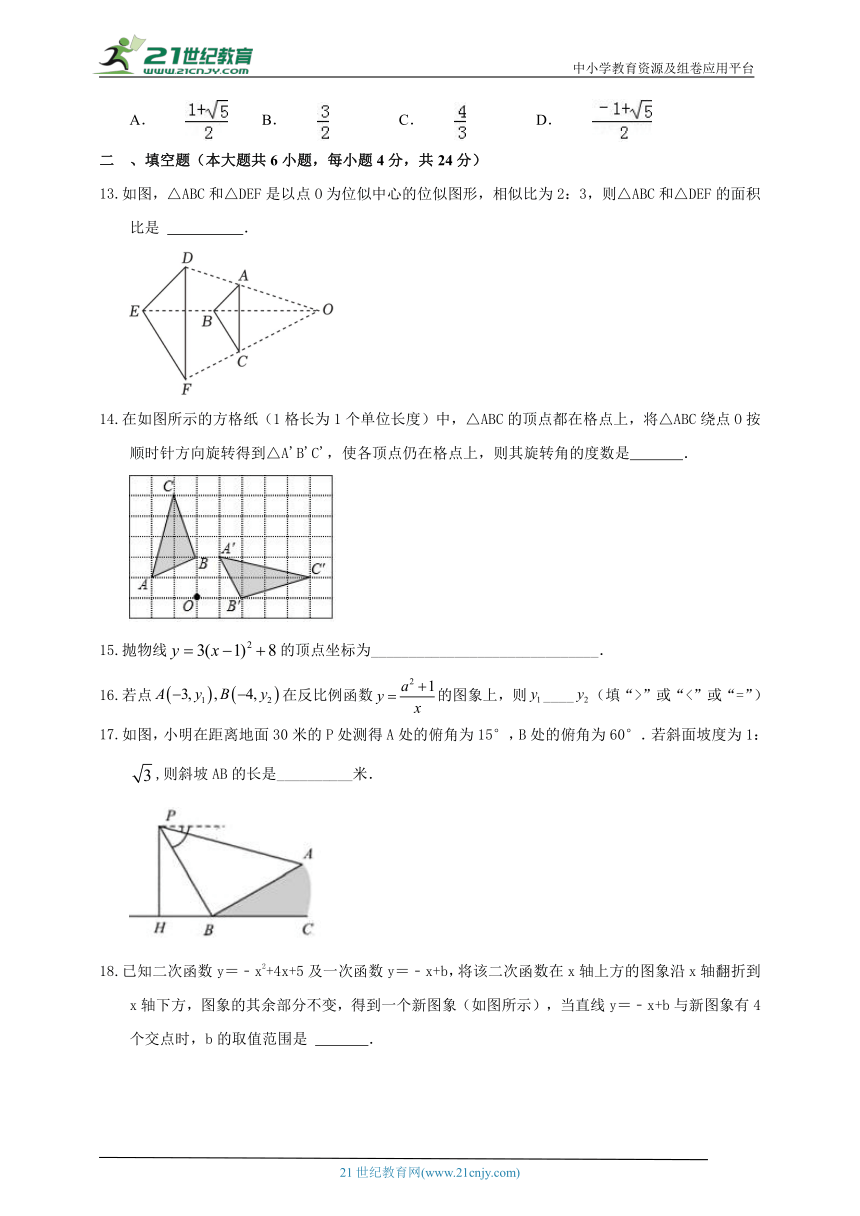
如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆,AB=b,AB的最大仰角为α.当∠C=45°时,则点A到桌面的最大高度是( )
A. B. C.a+bcosα D.a+bsinα
如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为( )
A.8 B.12 C.14 D.16
如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是( )
A. B.C.D.
如图,反比例函数y=(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
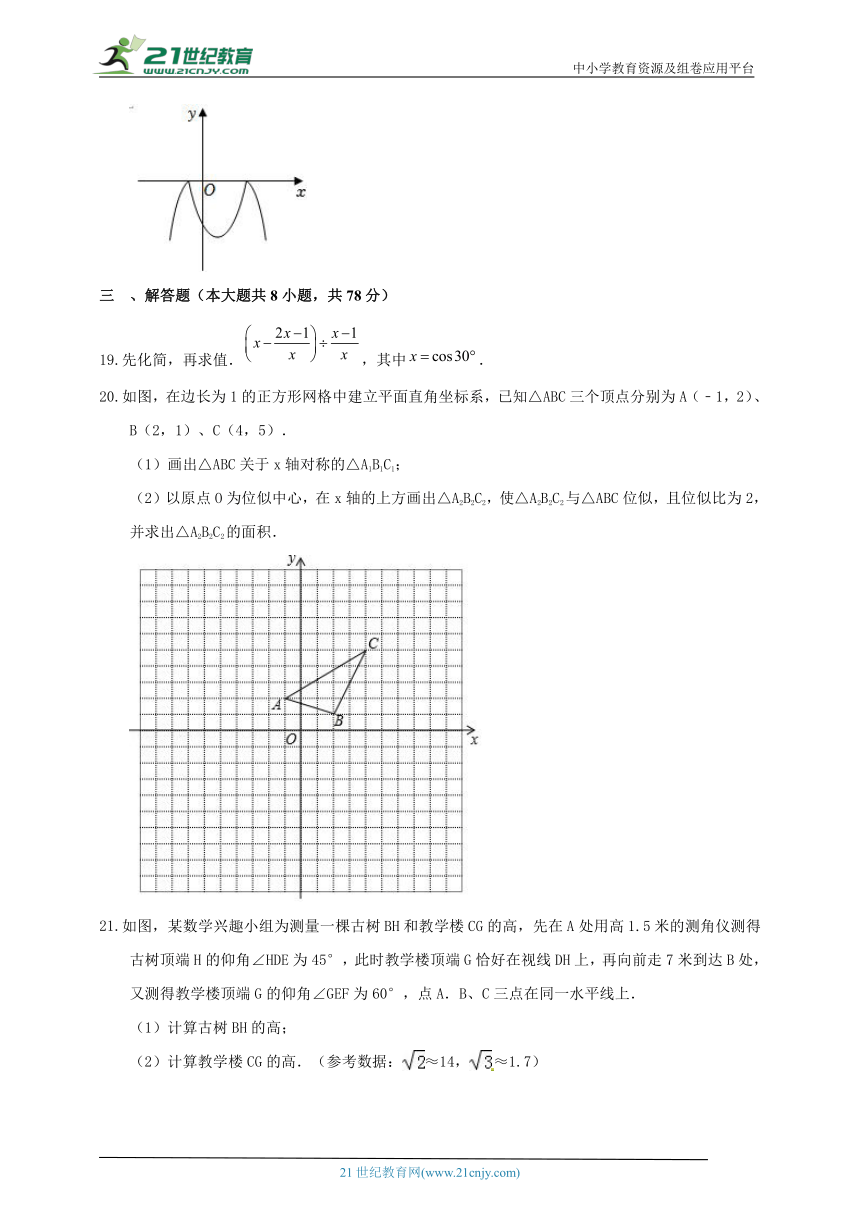
A. B. C. D.
1 、填空题(本大题共6小题,每小题4分,共24分)
如图,△ABC和△DEF是以点O为位似中心的位似图形,相似比为2:3,则△ABC和△DEF的面积比是 .
在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .
抛物线的顶点坐标为______________________________.
若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1:,则斜坡AB的长是__________米.
已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 .
1 、解答题(本大题共8小题,共78分)
先化简,再求值.,其中.
如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A.B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(参考数据:≈14,≈1.7)
如图,在平面直角坐标系xOy中,一次函数y=2x+b的图像分别与x轴、y轴交于点A.B,与反比例函数y=(x>0)的图像交于点C,连接OC.已知点B(0,4),△BOC的面积是2.
(1)求b、k的值,
(2)求△AOC的面积.
已知关于x的一元二次方程x2﹣(m+1)x+(m2+1)=0有实数根.
(1)求m的值;
(2)先作y=x2﹣(m+1)x+(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2﹣4n的最大值和最小值.
在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.
①若OE=,OG=1,求的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.
(1)求抛物线的表达式,
(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标,
(3)若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标,若不存在,请说明理由.
答案解析
1 、选择题
【考点】中心对称图形,轴对称图形.
【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意,
B.是轴对称图形,不是中心对称图形,故本选项不符合题意,
C.不是轴对称图形,是中心对称图形,故本选项不符合题意,
D.是轴对称图形,不是中心对称图形,故本选项不符合题意.
故选:A.
【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
【考点】三角函数的定义
【分析】根据三角函数的定义进行判断,即可解决问题.
解:∵中,,、、所对的边分别为a、b、c
∴,即,则A选项不成立,B选项成立
,即,则C、D选项均不成立
故选:B.
【点评】本题考查了三角函数的定义,熟记定义是解题关键.
【考点】黄金分割,算术平均数,中位数,众数,统计量的选择.
【分析】根据黄金分割的定义,即可解答.
解:我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了黄金分割数,
故选:A.
【点评】本题考查了黄金分割,算术平均数,中位线,众数,统计量的选择,熟练掌握这些数学知识是解题的关键.
【考点】二次函数的性质.
【分析】由抛物线解析式可得抛物线顶点坐标.
解:∵y=2(x+9)2﹣3,
∴抛物线顶点坐标为(﹣9,﹣3),
故选:B.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数的顶点式.
【考点】相似三角形的应用
【分析】先求出两个高脚杯液体的高度,再通过三角形相似,建立其对应边的比与对应高的比相等的关系,即可求出AB.
解:由题可知,第一个高脚杯盛液体的高度为:15-7=8(cm),
第二个高脚杯盛液体的高度为:11-7=4(cm),
因为液面都是水平的,图1和图2中的高脚杯是同一个高脚杯,
所以图1和图2中的两个三角形相似,
∴,
∴(cm),
故选:C.
【点评】本题考查了相似三角形的判定与性质,解决本题的关键是读懂题意,与图形建立关联,能灵活运用相似三角形的判定得到相似三角形,并能运用其性质得到相应线段之间的关系等,本题对学生的观察分析的能力有一定的要求.
【考点】勾股定理的应用,垂径定理的应用
【分析】根据题意,可以推出AD=BD=20,若设半径为r,则OD=r﹣10,OB=r,结合勾股定理可推出半径r的值.
解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m
故选:A.
【点评】本题主要考查垂径定理的应用、勾股定理的应用,关键在于设出半径为r后,用r表示出OD、OB的长度.
【考点】抛物线与x轴的交点,二次函数的性质,二次函数图象上点的坐标特征,二次函数的最值.
【分析】根据表格中的数据,可以求出抛物线的解析式,然后化为顶点式和交点式,即可判断各个选项中的说法是否正确.
解:由表格可得,
,
解得,
∴y=﹣x2+x+6=﹣(x﹣)2+=(﹣x+3)(x+2),
∴该抛物线的开口向下,故选项A正确,不符合题意,
该抛物线的对称轴是直线x=,故选项B正确,不符合题意,
∵当x=﹣2时,y=0,
∴当x=×2﹣(﹣2)=3时,y=0,故选项C错误,符合题意,
函数y=ax2+bx+c的最大值为,故选项D正确,不符合题意,
故选:C.
【点评】本题考查抛物线与x轴的交点、二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,求出抛物线的解析式.
【考点】反比例函数与一次函数的交点问题
【分析】一次函数y1=kx+b落在与反比例函数y2=图象上方的部分对应的自变量的取值范围即为所求.
解:∵一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,
∴不等式y1>y2的解集是﹣3<x<0或x>2.
故选:C.
【点评】本题考查了反比例函数与一次函数的交点问题,利用数形结合是解题的关键.
【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】过点A作AF⊥BE于F,过点B作BG⊥CD于G,利用解直角三角形可得AF=bsinα,BG=a,根据点A到桌面的最大高度=BG+AF,即可求得答案
解:如图,过点A作AF⊥BE于F,过点B作BG⊥CD于G,
在Rt△ABF中,AF=AB sinα=bsinα,
在Rt△BCG中,BG=BC sin45°=a×=a,
∴点A到桌面的最大高度=BG+AF=a+bsinα,
故选:D.
【点评】本题考查了解直角三角形的应用,解题关键是添加辅助线,构造直角三角形,利用解直角三角形解决问题.
【考点】三角形中位线定理;相似三角形的判定与性质
【分析】直接利用三角形中位线定理得出DE∥BC,DE=BC,再利用相似三角形的判定与性质得出答案.
解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,
∵=,
∴=,
∵△ADE的面积为4,
∴△ABC的面积为:16,
故选:D.
【点评】此题主要考查了三角形的中位线以及相似三角形的判定与性质,正确得出△ADE∽△ABC是解题关键.
【考点】一次函数的图象;二次函数的性质
【分析】根据二次函数的图象可以判断a、b、a﹣b的正负情况,从而可以得到一次函数经过哪几个象限,本题得以解决.
解:由二次函数的图象可知,
a<0,b<0,
当x=﹣1时,y=a﹣b<0,
∴y=(a﹣b)x+b的图象在第二、三、四象限,
故选:D.
【点评】本题考查二次函数的性质、一次函数的性质,解答本题的关键是明确题意,利用函数的思想解答.
【考点】反比例函数综合题..
【分析】根据反比例函数图象上点的坐标特征由A点坐标为(﹣1,1)得到k=﹣1,即反比例函数解析式为y=﹣,且OB=AB=1,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则B点的坐标可表示为(﹣,t),于是利用PB=PB′得t﹣1=|﹣|=,然后解方程可得到满足条件的t的值.
解:如图,
∵A点坐标为(﹣1,1),
∴k=﹣1×1=﹣1,
∴反比例函数解析式为y=﹣,
∵OB=AB=1,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠BPQ=∠B′PQ=45°,即∠B′PB=90°,
∴B′P⊥y轴,
∴B点的坐标为(﹣,t),
∵PB=PB′,
∴t﹣1=|﹣|=,
整理得t2﹣t﹣1=0,解得t1=,t2=(舍去),
∴t的值为.
故选A.
【点评】本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、等腰直角三角形的性质和轴对称的性质;会用求根公式法解一元二次方程.
1 、填空题
【考点】位似变换.
【分析】先利用位似的性质得到△ABC∽△DEF,相似比为2:3,然后根据相似三角形的性质解决问题.
解:∵△ABC与△DEF是以点O为位似中心的位似图形,位似比为2:3,
∴△ABC∽△DEF,相似比为2:3,
∴△ABC与△DEF的面积之比为22:32=4:9.
故答案为:4:9.
【点评】本题考查的是位似变换的概念和性质、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.
【考点】旋转的性质
【分析】根据旋转角的概念找到∠BOB′是旋转角,从图形中可求出其度数.
解:根据旋转角的概念:对应点与旋转中心连线的夹角,可知∠BOB′是旋转角,且∠BOB′=90°,
故答案为90°.
【点评】本题主要考查了旋转角的概念,解题的关键是根据旋转角的概念找到旋转角.
【考点】二次函数的性质
【分析】根据题意可知,本题考察二次函数的性质,根据二次函数的顶点式,进行求解.
解:由二次函数性质可知,的顶点坐标为(,)
∴的顶点坐标为(1,8)
故答案为:(1,8)
【点评】本题考查了二次函数的性质,先把函数解析式配成顶点式根据顶点式即可得到顶点坐标.
【考点】反比例函数的图象,反比例函数的性质,反比例函数图象上点的坐标特征
【分析】先确定的图像在一,三象限,且在每一象限内,随的增大而减小,再利用反比例函数的性质可得答案.
解:>
的图像在一,三象限,且在每一象限内,随的增大而减小,
>
<
故答案为:
【点评】本题考查的是反比例函数的性质,掌握利用反比例函数的图像与性质比较函数值的大小是解题的关键.
【考点】解直角三角形的应用-仰角俯角问题
【分析】首先根据题意得出∠ABF=30°,进而得出∠PBA=90°,∠BAP=45°,再利用锐角三角函数关系求出即可.
解:如图所示:过点A作AF⊥BC于点F,
∵斜面坡度为1:,
∴tan∠ABF=,
∴∠ABF=30°,
∵在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°,
∴∠HPB=30°,∠APB=45°,
∴∠HBP=60°,
∴∠PBA=90°,∠BAP=45°,
∴PB=AB,
∵PH=30m,sin60°=,
解得:PB=,
故AB=m,
故答案为:.
【点评】此题主要考查了解直角三角形的应用,正确得出PB=AB是解题关键.
【考点】二次函数图象与几何变换.
【分析】解方程﹣x2+4x+5=0得A(﹣1,0),B(5,0),再利用折叠的性质求出折叠部分的解析式为y=(x+1)(x﹣5),即y=x2﹣4x﹣5(﹣1≤x≤5),然后求出直线y=﹣x+b经过点A(﹣1,0)时b的值和当直线y=﹣x+b与抛物线y=x2﹣4x﹣5(﹣1≤x≤5)有唯一公共点时b的值,从而得到当直线y=﹣x+b与新图象有4个交点时,b的取值范围.
解:如图,当y=0时,﹣x2+4x+5=0,解得x1=﹣1,x2=5,则A(﹣1,0),B(5,0),
将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+1)(x﹣5),
即y=x2﹣4x﹣5(﹣1≤x≤5),
当直线y=﹣x+b经过点A(﹣1,0)时,1+b=0,解得b=﹣1;
当直线y=﹣x+b与抛物线y=x2﹣4x﹣5(﹣1≤x≤5)有唯一公共点时,方程x2﹣4x﹣5=﹣x+b有相等的实数解,解得b=﹣,
所以当直线y=﹣x+b与新图象有4个交点时,b的取值范围为﹣<b<﹣1.
故答案为:﹣<b<﹣1.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数图象与几何变换.
1 、解答题
【考点】分式的化简求值,特殊角的三角函数值
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解:
.
当时,
原式.
【点评】此题考查了分式的化简求值,涉及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.
【考点】作图﹣位似变换;作图﹣轴对称变换.
【分析】(1)画出A.B、C关于x轴的对称点A1、B1、C1即可解决问题;
(2)连接OB延长OB到B2,使得OB=BB2,同法可得A2、C2,△A2B2C2就是所求三角形;
解:(1)如图所示,△A1B1C1就是所求三角形
(2)如图所示,△A2B2C2就是所求三角形
如图,分别过点A2、C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E、F,
∵A(﹣1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且位似比为2,
∴A2(﹣2,4),B2(4,2),C2(8,10),
∴=8×10﹣×6×2﹣×4×8﹣×6×10=28.
【点评】本题考查作图-位似变换,作图轴对称变换等知识,解题的关键是理解位似变换、轴对称变换的定义,属于中考常考题型.
【考点】解直角三角形的应用﹣仰角俯角问题
【分析】(1)利用等腰直角三角形的性质即可解决问题;
(2)作HJ⊥CG于G.则△HJG是等腰三角形,四边形BCJH是矩形,设HJ=GJ=BC=x.构建方程即可解决问题;
解:(1)由题意:四边形ABED是矩形,可得DE=AB=7米.
在Rt△DEH中,∵∠EDH=45°,
∴HE=DE=7米.
(2)作HJ⊥CG于G.则△HJG是等腰三角形,四边形BCJH是矩形,设HJ=GJ=BC=x.
在Rt△BCG中,tan60°=,
∴=,
∴x=+.
∴CG=CF+FG=×1.7+3.5+1.5=11.3米.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
【考点】反比例函数与一次函数的交点问题.
【分析】(1)由点B(0,4)在一次函数y=2x+b的图象上,代入求得b=4,由△BOC的面积是2得出C的横坐标为1,代入直线关系式即可求出C的坐标,从而求出k的值,
(2)根据一次函数的解析式求得A的坐标,然后根据三角形的面积公式代入计算即可.
解:(1)∵一次函数y=2x+b的图象过点B(0,4),
∴b=4,
∴一次函数为y=2x+4,
∵OB=4,△BOC的面积是2.
∴OB xC=2,即=2,
∴xC=1,
把x=1代入y=2x+4得,y=6,
∴C(1,6),
∵点C在反比例函数y=(x>0)的图象上,
∴k=1×6=6,
(2)把y=0代入y=2x+4得,2x+4=0,解得x=﹣2,
∴A(﹣2,0),
∴OA=2,
∴S△AOC==6.
【点评】本题是一次函数与反比例函数的交点问题,考查了待定系数法求函数的解析式,一次函数图象上点的坐标特征,三角形的面积,求出C的坐标是解题的关键.
【考点】抛物线与x轴的交点;根的判别式;二次函数图象与几何变换;二次函数的最值.
【分析】(1)由题意△≥0,列出不等式,解不等式即可;
(2)画出翻折.平移后的图象,根据顶点坐标即可写出函数的解析式;
(3)首先确定n的取值范围,利用二次函数的性质即可解决问题;
解:(1)对于一元二次方程x2﹣(m+1)x+(m2+1)=0,
△=(m+1)2﹣2(m2+1)=﹣m2+2m﹣1=﹣(m﹣1)2,
∵方程有实数根,
∴﹣(m﹣1)2≥0,
∴m=1.
(2)由(1)可知y=x2﹣2x+1=(x﹣1)2,
图象如图所示:
平移后的解析式为y=﹣(x+2)2+2=﹣x2﹣4x﹣2.
(3)由消去y得到x2+6x+n+2=0,
由题意△≥0,
∴36﹣4n﹣8≥0,
∴n≤7,
∵n≤m,m=1,
∴1≤n≤7,
令y′=n2﹣4n=(n﹣2)2﹣4,
∴n=2时,y′的值最小,最小值为﹣4,
n=7时,y′的值最大,最大值为21,
∴n2﹣4n的最大值为21,最小值为﹣4.
【点评】本题考查抛物线与x轴的交点、待定系数法、翻折变换、平移变换、二次函数的最值问题等知识,解题的关键是理解题意,学会用转化的思想思考问题,属于中考常考题型.
【考点】平行四边形的判定,旋转的性质
【分析】(1)如图1,利用旋转的性质得CA=DA,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,再根据等腰三角形的性质求出∠ADC,从而计算出∠CDE的度数;
(2)如图2,利用直角三角形斜边上的中线性质得到BF=AC,利用含30度的直角三角形三边的关系得到BC=AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴CA=CD,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=(180° 30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75° 60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠BAC=30°,
∴BC=AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定.
【考点】相似形综合题
【分析】(1)连接AC,由四个中点可知OE∥AC、OE=AC,GF∥AC、GF=AC,据此得出OE=GF、OE=GF,即可得证;
(2)①由旋转性质知OG=OM、OE=ON,∠GOM=∠EON,据此可证△OGM∽△OEN得==;
②连接AC、BD,根据①知△OGM∽△OEN,若要GM=EN只需使△OGM≌△OEN,添加使AC=BD的条件均可以满足此条件.
解:(1)如图1,连接AC,
∵点O、E、F、G分别是AB、BC、CD、AD的中点,
∴OE∥AC、OE=AC,GF∥AC、GF=AC,
∴OE∥GF,OE=GF,
∴四边形OEFG是平行四边形;
(2)①∵△OGE绕点O顺时针旋转得到△OMN,
∴OG=OM、OE=ON,∠GOM=∠EON,
∴=,
∴△OGM∽△OEN,
∴==.
②添加AC=BD,
如图2,连接AC、BD,
∵点O、E、F、G分别是AB、BC、CD、AD的中点,
∴OG=EF=BD、OE=GF=AC,
∵AC=BD,
∴OG=OE,
∵△OGE绕点O顺时针旋转得到△OMN,
∴OG=OM、OE=ON,∠GOM=∠EON,
∴OG=OE、OM=ON,
在△OGM和△OEN中,
∵,
∴△OGM≌△OEN(SAS),
∴GM=EN.
【点评】本题主要考查相似形的综合题,解题的关键是熟练掌握中位线定义及其定理、平行四边形的判定、旋转的性质、相似三角形与全等三角形的判定与性质等知识点.
【考点】二次函数综合题.
【分析】(1)先求得A,C,B三点的坐标,将抛物线设为交点式,进一步求得结果,
(2)作DF⊥AB于F,交AC于E,根据点D和点E坐标可表示出DE的长,进而表示出三角形ADC的面积,进而表示出S的函数关系式,进一步求得结果,
(3)根据菱形性质可得PA=PC,进而求得点P的坐标,根据菱形性质,进一步求得点Q坐标.
解:(1)当x=0时,y=4,
∴C (0,4),
当y=0时,x+4=0,
∴x=﹣3,
∴A (﹣3,0),
∵对称轴为直线x=﹣1,
∴B(1,0),
∴设抛物线的表达式:y=a(x﹣1) (x+3),
∴4=﹣3a,
∴a=﹣,
∴抛物线的表达式为:y=﹣(x﹣1) (x+3)=﹣x2﹣x+4,
(2)如图1,
作DF⊥AB于F,交AC于E,
∴D(m,﹣﹣m+4),E(m,﹣m+4),
∴DE=﹣﹣m+4﹣(m+4)=﹣m2﹣4m,
∴S△ADC=OA= (﹣m2﹣4m)=﹣2m2﹣6m,
∵S△ABC===8,
∴S=﹣2m2﹣6m+8=﹣2(m+)2+,
∴当m=﹣时,S最大=,
当m=﹣时,y=﹣=5,
∴D(﹣,5),
(3)设P(﹣1,n),
∵以A,C,P,Q为顶点的四边形是以AC为对角线的菱形,
∴PA=PC,
即:PA2=PC2,
∴(﹣1+3)2+n2=1+(n﹣4)2,
∴n=,
∴P(﹣1,),
∵xP+xQ=xA+xC,yP+yQ=yA+yC
∴xQ=﹣3﹣(﹣1)=﹣2,yQ=4﹣=,
∴Q(﹣2,).
【点评】本题考查了二次函数及其图象性质,勾股定理,菱形性质等知识,解决问题的关键是熟练掌握相关二次函数和菱形性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版2023-2024九年级上期末模拟试题3
考试范围:九上-九下24.2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
如图,在中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了( )
A.黄金分割数 B.平均数 C.众数 D.中位数
抛物线y=2(x+9)2﹣3的顶点坐标是( )
A.(9,﹣3) B.(﹣9,﹣3) C.(9,3) D.(﹣9,3)
图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B. C. D.
如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m B.24m C.30m D.60m
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x ﹣2 ﹣1 0 1
y 0 4 6 6
下列结论不正确的是( )
A.抛物线的开口向下
B.抛物线的对称轴为直线x=
C.抛物线与x轴的一个交点坐标为(2,0)
D.函数y=ax2+bx+c的最大值为
如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
A.﹣3<x<2
B.x<﹣3或x>2
C.﹣3<x<0或x>2
D.0<x<2
如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆,AB=b,AB的最大仰角为α.当∠C=45°时,则点A到桌面的最大高度是( )
A. B. C.a+bcosα D.a+bsinα
如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为( )
A.8 B.12 C.14 D.16
如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是( )
A. B.C.D.
如图,反比例函数y=(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A. B. C. D.
1 、填空题(本大题共6小题,每小题4分,共24分)
如图,△ABC和△DEF是以点O为位似中心的位似图形,相似比为2:3,则△ABC和△DEF的面积比是 .
在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .
抛物线的顶点坐标为______________________________.
若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1:,则斜坡AB的长是__________米.
已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 .
1 、解答题(本大题共8小题,共78分)
先化简,再求值.,其中.
如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A.B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(参考数据:≈14,≈1.7)
如图,在平面直角坐标系xOy中,一次函数y=2x+b的图像分别与x轴、y轴交于点A.B,与反比例函数y=(x>0)的图像交于点C,连接OC.已知点B(0,4),△BOC的面积是2.
(1)求b、k的值,
(2)求△AOC的面积.
已知关于x的一元二次方程x2﹣(m+1)x+(m2+1)=0有实数根.
(1)求m的值;
(2)先作y=x2﹣(m+1)x+(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2﹣4n的最大值和最小值.
在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.
①若OE=,OG=1,求的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.
(1)求抛物线的表达式,
(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标,
(3)若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标,若不存在,请说明理由.
答案解析
1 、选择题
【考点】中心对称图形,轴对称图形.
【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意,
B.是轴对称图形,不是中心对称图形,故本选项不符合题意,
C.不是轴对称图形,是中心对称图形,故本选项不符合题意,
D.是轴对称图形,不是中心对称图形,故本选项不符合题意.
故选:A.
【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
【考点】三角函数的定义
【分析】根据三角函数的定义进行判断,即可解决问题.
解:∵中,,、、所对的边分别为a、b、c
∴,即,则A选项不成立,B选项成立
,即,则C、D选项均不成立
故选:B.
【点评】本题考查了三角函数的定义,熟记定义是解题关键.
【考点】黄金分割,算术平均数,中位数,众数,统计量的选择.
【分析】根据黄金分割的定义,即可解答.
解:我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了黄金分割数,
故选:A.
【点评】本题考查了黄金分割,算术平均数,中位线,众数,统计量的选择,熟练掌握这些数学知识是解题的关键.
【考点】二次函数的性质.
【分析】由抛物线解析式可得抛物线顶点坐标.
解:∵y=2(x+9)2﹣3,
∴抛物线顶点坐标为(﹣9,﹣3),
故选:B.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数的顶点式.
【考点】相似三角形的应用
【分析】先求出两个高脚杯液体的高度,再通过三角形相似,建立其对应边的比与对应高的比相等的关系,即可求出AB.
解:由题可知,第一个高脚杯盛液体的高度为:15-7=8(cm),
第二个高脚杯盛液体的高度为:11-7=4(cm),
因为液面都是水平的,图1和图2中的高脚杯是同一个高脚杯,
所以图1和图2中的两个三角形相似,
∴,
∴(cm),
故选:C.
【点评】本题考查了相似三角形的判定与性质,解决本题的关键是读懂题意,与图形建立关联,能灵活运用相似三角形的判定得到相似三角形,并能运用其性质得到相应线段之间的关系等,本题对学生的观察分析的能力有一定的要求.
【考点】勾股定理的应用,垂径定理的应用
【分析】根据题意,可以推出AD=BD=20,若设半径为r,则OD=r﹣10,OB=r,结合勾股定理可推出半径r的值.
解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m
故选:A.
【点评】本题主要考查垂径定理的应用、勾股定理的应用,关键在于设出半径为r后,用r表示出OD、OB的长度.
【考点】抛物线与x轴的交点,二次函数的性质,二次函数图象上点的坐标特征,二次函数的最值.
【分析】根据表格中的数据,可以求出抛物线的解析式,然后化为顶点式和交点式,即可判断各个选项中的说法是否正确.
解:由表格可得,
,
解得,
∴y=﹣x2+x+6=﹣(x﹣)2+=(﹣x+3)(x+2),
∴该抛物线的开口向下,故选项A正确,不符合题意,
该抛物线的对称轴是直线x=,故选项B正确,不符合题意,
∵当x=﹣2时,y=0,
∴当x=×2﹣(﹣2)=3时,y=0,故选项C错误,符合题意,
函数y=ax2+bx+c的最大值为,故选项D正确,不符合题意,
故选:C.
【点评】本题考查抛物线与x轴的交点、二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,求出抛物线的解析式.
【考点】反比例函数与一次函数的交点问题
【分析】一次函数y1=kx+b落在与反比例函数y2=图象上方的部分对应的自变量的取值范围即为所求.
解:∵一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,
∴不等式y1>y2的解集是﹣3<x<0或x>2.
故选:C.
【点评】本题考查了反比例函数与一次函数的交点问题,利用数形结合是解题的关键.
【考点】解直角三角形的应用﹣仰角俯角问题.
【分析】过点A作AF⊥BE于F,过点B作BG⊥CD于G,利用解直角三角形可得AF=bsinα,BG=a,根据点A到桌面的最大高度=BG+AF,即可求得答案
解:如图,过点A作AF⊥BE于F,过点B作BG⊥CD于G,
在Rt△ABF中,AF=AB sinα=bsinα,
在Rt△BCG中,BG=BC sin45°=a×=a,
∴点A到桌面的最大高度=BG+AF=a+bsinα,
故选:D.
【点评】本题考查了解直角三角形的应用,解题关键是添加辅助线,构造直角三角形,利用解直角三角形解决问题.
【考点】三角形中位线定理;相似三角形的判定与性质
【分析】直接利用三角形中位线定理得出DE∥BC,DE=BC,再利用相似三角形的判定与性质得出答案.
解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,
∵=,
∴=,
∵△ADE的面积为4,
∴△ABC的面积为:16,
故选:D.
【点评】此题主要考查了三角形的中位线以及相似三角形的判定与性质,正确得出△ADE∽△ABC是解题关键.
【考点】一次函数的图象;二次函数的性质
【分析】根据二次函数的图象可以判断a、b、a﹣b的正负情况,从而可以得到一次函数经过哪几个象限,本题得以解决.
解:由二次函数的图象可知,
a<0,b<0,
当x=﹣1时,y=a﹣b<0,
∴y=(a﹣b)x+b的图象在第二、三、四象限,
故选:D.
【点评】本题考查二次函数的性质、一次函数的性质,解答本题的关键是明确题意,利用函数的思想解答.
【考点】反比例函数综合题..
【分析】根据反比例函数图象上点的坐标特征由A点坐标为(﹣1,1)得到k=﹣1,即反比例函数解析式为y=﹣,且OB=AB=1,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则B点的坐标可表示为(﹣,t),于是利用PB=PB′得t﹣1=|﹣|=,然后解方程可得到满足条件的t的值.
解:如图,
∵A点坐标为(﹣1,1),
∴k=﹣1×1=﹣1,
∴反比例函数解析式为y=﹣,
∵OB=AB=1,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠BPQ=∠B′PQ=45°,即∠B′PB=90°,
∴B′P⊥y轴,
∴B点的坐标为(﹣,t),
∵PB=PB′,
∴t﹣1=|﹣|=,
整理得t2﹣t﹣1=0,解得t1=,t2=(舍去),
∴t的值为.
故选A.
【点评】本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、等腰直角三角形的性质和轴对称的性质;会用求根公式法解一元二次方程.
1 、填空题
【考点】位似变换.
【分析】先利用位似的性质得到△ABC∽△DEF,相似比为2:3,然后根据相似三角形的性质解决问题.
解:∵△ABC与△DEF是以点O为位似中心的位似图形,位似比为2:3,
∴△ABC∽△DEF,相似比为2:3,
∴△ABC与△DEF的面积之比为22:32=4:9.
故答案为:4:9.
【点评】本题考查的是位似变换的概念和性质、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.
【考点】旋转的性质
【分析】根据旋转角的概念找到∠BOB′是旋转角,从图形中可求出其度数.
解:根据旋转角的概念:对应点与旋转中心连线的夹角,可知∠BOB′是旋转角,且∠BOB′=90°,
故答案为90°.
【点评】本题主要考查了旋转角的概念,解题的关键是根据旋转角的概念找到旋转角.
【考点】二次函数的性质
【分析】根据题意可知,本题考察二次函数的性质,根据二次函数的顶点式,进行求解.
解:由二次函数性质可知,的顶点坐标为(,)
∴的顶点坐标为(1,8)
故答案为:(1,8)
【点评】本题考查了二次函数的性质,先把函数解析式配成顶点式根据顶点式即可得到顶点坐标.
【考点】反比例函数的图象,反比例函数的性质,反比例函数图象上点的坐标特征
【分析】先确定的图像在一,三象限,且在每一象限内,随的增大而减小,再利用反比例函数的性质可得答案.
解:>
的图像在一,三象限,且在每一象限内,随的增大而减小,
>
<
故答案为:
【点评】本题考查的是反比例函数的性质,掌握利用反比例函数的图像与性质比较函数值的大小是解题的关键.
【考点】解直角三角形的应用-仰角俯角问题
【分析】首先根据题意得出∠ABF=30°,进而得出∠PBA=90°,∠BAP=45°,再利用锐角三角函数关系求出即可.
解:如图所示:过点A作AF⊥BC于点F,
∵斜面坡度为1:,
∴tan∠ABF=,
∴∠ABF=30°,
∵在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°,
∴∠HPB=30°,∠APB=45°,
∴∠HBP=60°,
∴∠PBA=90°,∠BAP=45°,
∴PB=AB,
∵PH=30m,sin60°=,
解得:PB=,
故AB=m,
故答案为:.
【点评】此题主要考查了解直角三角形的应用,正确得出PB=AB是解题关键.
【考点】二次函数图象与几何变换.
【分析】解方程﹣x2+4x+5=0得A(﹣1,0),B(5,0),再利用折叠的性质求出折叠部分的解析式为y=(x+1)(x﹣5),即y=x2﹣4x﹣5(﹣1≤x≤5),然后求出直线y=﹣x+b经过点A(﹣1,0)时b的值和当直线y=﹣x+b与抛物线y=x2﹣4x﹣5(﹣1≤x≤5)有唯一公共点时b的值,从而得到当直线y=﹣x+b与新图象有4个交点时,b的取值范围.
解:如图,当y=0时,﹣x2+4x+5=0,解得x1=﹣1,x2=5,则A(﹣1,0),B(5,0),
将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+1)(x﹣5),
即y=x2﹣4x﹣5(﹣1≤x≤5),
当直线y=﹣x+b经过点A(﹣1,0)时,1+b=0,解得b=﹣1;
当直线y=﹣x+b与抛物线y=x2﹣4x﹣5(﹣1≤x≤5)有唯一公共点时,方程x2﹣4x﹣5=﹣x+b有相等的实数解,解得b=﹣,
所以当直线y=﹣x+b与新图象有4个交点时,b的取值范围为﹣<b<﹣1.
故答案为:﹣<b<﹣1.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数图象与几何变换.
1 、解答题
【考点】分式的化简求值,特殊角的三角函数值
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解:
.
当时,
原式.
【点评】此题考查了分式的化简求值,涉及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.
【考点】作图﹣位似变换;作图﹣轴对称变换.
【分析】(1)画出A.B、C关于x轴的对称点A1、B1、C1即可解决问题;
(2)连接OB延长OB到B2,使得OB=BB2,同法可得A2、C2,△A2B2C2就是所求三角形;
解:(1)如图所示,△A1B1C1就是所求三角形
(2)如图所示,△A2B2C2就是所求三角形
如图,分别过点A2、C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E、F,
∵A(﹣1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且位似比为2,
∴A2(﹣2,4),B2(4,2),C2(8,10),
∴=8×10﹣×6×2﹣×4×8﹣×6×10=28.
【点评】本题考查作图-位似变换,作图轴对称变换等知识,解题的关键是理解位似变换、轴对称变换的定义,属于中考常考题型.
【考点】解直角三角形的应用﹣仰角俯角问题
【分析】(1)利用等腰直角三角形的性质即可解决问题;
(2)作HJ⊥CG于G.则△HJG是等腰三角形,四边形BCJH是矩形,设HJ=GJ=BC=x.构建方程即可解决问题;
解:(1)由题意:四边形ABED是矩形,可得DE=AB=7米.
在Rt△DEH中,∵∠EDH=45°,
∴HE=DE=7米.
(2)作HJ⊥CG于G.则△HJG是等腰三角形,四边形BCJH是矩形,设HJ=GJ=BC=x.
在Rt△BCG中,tan60°=,
∴=,
∴x=+.
∴CG=CF+FG=×1.7+3.5+1.5=11.3米.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
【考点】反比例函数与一次函数的交点问题.
【分析】(1)由点B(0,4)在一次函数y=2x+b的图象上,代入求得b=4,由△BOC的面积是2得出C的横坐标为1,代入直线关系式即可求出C的坐标,从而求出k的值,
(2)根据一次函数的解析式求得A的坐标,然后根据三角形的面积公式代入计算即可.
解:(1)∵一次函数y=2x+b的图象过点B(0,4),
∴b=4,
∴一次函数为y=2x+4,
∵OB=4,△BOC的面积是2.
∴OB xC=2,即=2,
∴xC=1,
把x=1代入y=2x+4得,y=6,
∴C(1,6),
∵点C在反比例函数y=(x>0)的图象上,
∴k=1×6=6,
(2)把y=0代入y=2x+4得,2x+4=0,解得x=﹣2,
∴A(﹣2,0),
∴OA=2,
∴S△AOC==6.
【点评】本题是一次函数与反比例函数的交点问题,考查了待定系数法求函数的解析式,一次函数图象上点的坐标特征,三角形的面积,求出C的坐标是解题的关键.
【考点】抛物线与x轴的交点;根的判别式;二次函数图象与几何变换;二次函数的最值.
【分析】(1)由题意△≥0,列出不等式,解不等式即可;
(2)画出翻折.平移后的图象,根据顶点坐标即可写出函数的解析式;
(3)首先确定n的取值范围,利用二次函数的性质即可解决问题;
解:(1)对于一元二次方程x2﹣(m+1)x+(m2+1)=0,
△=(m+1)2﹣2(m2+1)=﹣m2+2m﹣1=﹣(m﹣1)2,
∵方程有实数根,
∴﹣(m﹣1)2≥0,
∴m=1.
(2)由(1)可知y=x2﹣2x+1=(x﹣1)2,
图象如图所示:
平移后的解析式为y=﹣(x+2)2+2=﹣x2﹣4x﹣2.
(3)由消去y得到x2+6x+n+2=0,
由题意△≥0,
∴36﹣4n﹣8≥0,
∴n≤7,
∵n≤m,m=1,
∴1≤n≤7,
令y′=n2﹣4n=(n﹣2)2﹣4,
∴n=2时,y′的值最小,最小值为﹣4,
n=7时,y′的值最大,最大值为21,
∴n2﹣4n的最大值为21,最小值为﹣4.
【点评】本题考查抛物线与x轴的交点、待定系数法、翻折变换、平移变换、二次函数的最值问题等知识,解题的关键是理解题意,学会用转化的思想思考问题,属于中考常考题型.
【考点】平行四边形的判定,旋转的性质
【分析】(1)如图1,利用旋转的性质得CA=DA,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,再根据等腰三角形的性质求出∠ADC,从而计算出∠CDE的度数;
(2)如图2,利用直角三角形斜边上的中线性质得到BF=AC,利用含30度的直角三角形三边的关系得到BC=AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴CA=CD,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=(180° 30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75° 60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠BAC=30°,
∴BC=AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定.
【考点】相似形综合题
【分析】(1)连接AC,由四个中点可知OE∥AC、OE=AC,GF∥AC、GF=AC,据此得出OE=GF、OE=GF,即可得证;
(2)①由旋转性质知OG=OM、OE=ON,∠GOM=∠EON,据此可证△OGM∽△OEN得==;
②连接AC、BD,根据①知△OGM∽△OEN,若要GM=EN只需使△OGM≌△OEN,添加使AC=BD的条件均可以满足此条件.
解:(1)如图1,连接AC,
∵点O、E、F、G分别是AB、BC、CD、AD的中点,
∴OE∥AC、OE=AC,GF∥AC、GF=AC,
∴OE∥GF,OE=GF,
∴四边形OEFG是平行四边形;
(2)①∵△OGE绕点O顺时针旋转得到△OMN,
∴OG=OM、OE=ON,∠GOM=∠EON,
∴=,
∴△OGM∽△OEN,
∴==.
②添加AC=BD,
如图2,连接AC、BD,
∵点O、E、F、G分别是AB、BC、CD、AD的中点,
∴OG=EF=BD、OE=GF=AC,
∵AC=BD,
∴OG=OE,
∵△OGE绕点O顺时针旋转得到△OMN,
∴OG=OM、OE=ON,∠GOM=∠EON,
∴OG=OE、OM=ON,
在△OGM和△OEN中,
∵,
∴△OGM≌△OEN(SAS),
∴GM=EN.
【点评】本题主要考查相似形的综合题,解题的关键是熟练掌握中位线定义及其定理、平行四边形的判定、旋转的性质、相似三角形与全等三角形的判定与性质等知识点.
【考点】二次函数综合题.
【分析】(1)先求得A,C,B三点的坐标,将抛物线设为交点式,进一步求得结果,
(2)作DF⊥AB于F,交AC于E,根据点D和点E坐标可表示出DE的长,进而表示出三角形ADC的面积,进而表示出S的函数关系式,进一步求得结果,
(3)根据菱形性质可得PA=PC,进而求得点P的坐标,根据菱形性质,进一步求得点Q坐标.
解:(1)当x=0时,y=4,
∴C (0,4),
当y=0时,x+4=0,
∴x=﹣3,
∴A (﹣3,0),
∵对称轴为直线x=﹣1,
∴B(1,0),
∴设抛物线的表达式:y=a(x﹣1) (x+3),
∴4=﹣3a,
∴a=﹣,
∴抛物线的表达式为:y=﹣(x﹣1) (x+3)=﹣x2﹣x+4,
(2)如图1,
作DF⊥AB于F,交AC于E,
∴D(m,﹣﹣m+4),E(m,﹣m+4),
∴DE=﹣﹣m+4﹣(m+4)=﹣m2﹣4m,
∴S△ADC=OA= (﹣m2﹣4m)=﹣2m2﹣6m,
∵S△ABC===8,
∴S=﹣2m2﹣6m+8=﹣2(m+)2+,
∴当m=﹣时,S最大=,
当m=﹣时,y=﹣=5,
∴D(﹣,5),
(3)设P(﹣1,n),
∵以A,C,P,Q为顶点的四边形是以AC为对角线的菱形,
∴PA=PC,
即:PA2=PC2,
∴(﹣1+3)2+n2=1+(n﹣4)2,
∴n=,
∴P(﹣1,),
∵xP+xQ=xA+xC,yP+yQ=yA+yC
∴xQ=﹣3﹣(﹣1)=﹣2,yQ=4﹣=,
∴Q(﹣2,).
【点评】本题考查了二次函数及其图象性质,勾股定理,菱形性质等知识,解决问题的关键是熟练掌握相关二次函数和菱形性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
