2023北京一六一中高二(上)期中数学(教师版)(含解析)
文档属性
| 名称 | 2023北京一六一中高二(上)期中数学(教师版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 275.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 17:44:44 | ||
图片预览




文档简介
2023北京一六一中高二(上)期中
数 学
一、选择题:本大题共10道小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项符合题目的要求。把正确答案涂写在答题卡上相应的位置。
1.已知A(﹣1,﹣3),B(3,5),则直线AB的斜率为( )
A.2 B.1 C. D.不存在
2.圆x2+y2﹣2x+4y+3=0的圆心坐标为( )
A.(﹣2,4) B.(2,﹣4) C.(1,﹣2) D.(﹣1,2)
3.两个焦点的坐标分别为(﹣3,0),(3,0)的椭圆上的任一点到两焦点的距离之和为8,则椭圆的标准方程
为( )
A.+=1 B.+=1
C.+=1 D.+=1
4.任意的k∈R,直线kx﹣y+1=3k恒过定点( )
A.(0,0) B.(0,1) C.(3,1) D.(2,1)
5.已知圆C1:x2+y2=1与圆C2:x2+y2﹣8x+7=0,则圆C1与圆C2的位置关系是( )
A.相离 B.相交 C.内切 D.外切
6.过点的直线l与圆有公共点,则直线l的倾斜角取值范围是( )
A. B. C. D.
7.“a=﹣1”是“直线l1:ax+4y﹣3=0与直线l2:x+(a﹣3)y+2=0”平行的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
8.如图,在平行六面体ABCD﹣A1B1C1D1中,AA1=AD=AB=2,∠BAD=,∠BAA1=∠A1AD=,则 =( )
A.12 B.8 C.6 D.4
9.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半.这条直线被后人称为三角形的欧拉线.已知△ABC的顶点A(2,0),B(1,2),且AC=BC,则△ABC的欧拉线的方程为( )
A.x﹣2y﹣4=0 B.2x+y﹣4=0 C.4x+2y+1=0 D.2x﹣4y+1=0
10.曲线C:x3+y3=1.给出下列结论:
①曲线C关于原点对称;
②曲线C上任意一点到原点的距离不小于1;
③曲线C只经过2个整点(即横、纵坐标均为整数的点).
其中,所有正确结论的序号是( )
A.①② B.② C.②③ D.③
二、填空题:本大题共5小题,共25分。把答案填在答题纸中相应的横线上。
11.(5分)已知空间向量=(2,3,1),=(﹣4,2,x),且⊥,则||= .
12.(5分)已知过点(0,2)的直线l的方向向量为(1,6),点A(a,b)在直线l上,则满足条件的一组a,b的值依次为 .
13.(5分)正方体中ABCD﹣A1B1C1D1,E是C1D1的中点,那么异面直线DE和AC所成角的余弦值等于 .
14.(5分)将一张坐标纸对折,如果点(0,m)与点(m﹣2,2)重合,则点(﹣4,1)与点 重合.
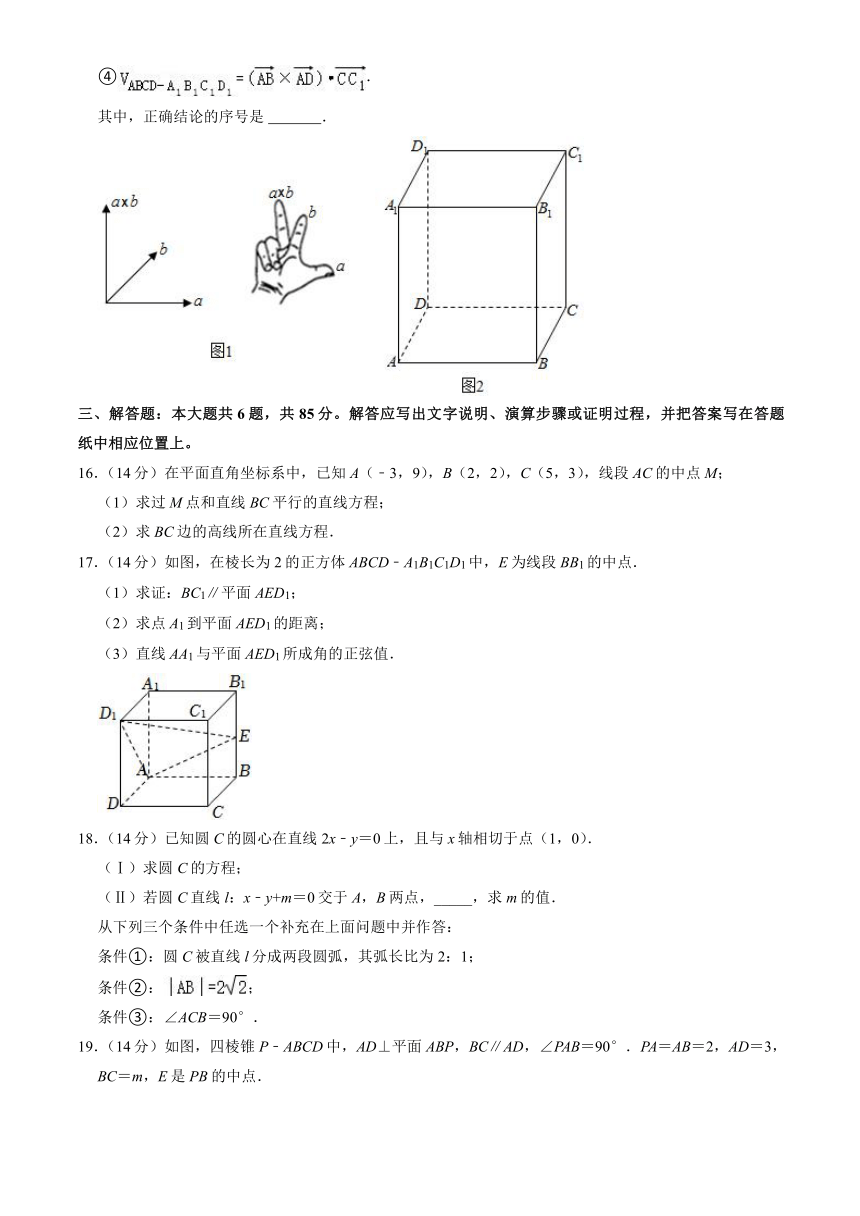
15.(5分)给定两个不共线的空间向量与,定义叉乘运算:.规定:
(ⅰ)为同时与,垂直的向量;
(ⅱ),,三个向量构成右手系(如图1);
(ⅲ).
如图2,在长方体ABCD﹣A1B1C1D1中,AB=AD=2,AA1=4.给出下列四个结论:
①;
②;
③;
④.
其中,正确结论的序号是 .
三、解答题:本大题共6题,共85分。解答应写出文字说明、演算步骤或证明过程,并把答案写在答题纸中相应位置上。
16.(14分)在平面直角坐标系中,已知A(﹣3,9),B(2,2),C(5,3),线段AC的中点M;
(1)求过M点和直线BC平行的直线方程;
(2)求BC边的高线所在直线方程.
17.(14分)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E为线段BB1的中点.
(1)求证:BC1∥平面AED1;
(2)求点A1到平面AED1的距离;
(3)直线AA1与平面AED1所成角的正弦值.
18.(14分)已知圆C的圆心在直线2x﹣y=0上,且与x轴相切于点(1,0).
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C直线l:x﹣y+m=0交于A,B两点,_____,求m的值.
从下列三个条件中任选一个补充在上面问题中并作答:
条件①:圆C被直线l分成两段圆弧,其弧长比为2:1;
条件②:;
条件③:∠ACB=90°.
19.(14分)如图,四棱锥P﹣ABCD中,AD⊥平面ABP,BC∥AD,∠PAB=90°.PA=AB=2,AD=3,BC=m,E是PB的中点.
(Ⅰ)证明:AE⊥平面PBC;
(Ⅱ)若二面角C﹣AE﹣D的余弦值是,求m的值;
(Ⅲ)若m=2,在线段AD上是否存在一点F,使得PF⊥CE.若存在,确定F点的位置;若不存在,说明理由.
20.(14分)已知圆C:(x﹣a)2+y2=1与直线y=﹣x﹣1交于M、N两点,点P为线段MN的中点,O为坐标原点,直线OP的斜率为.
(Ⅰ)求a的值及△MON的面积;
(Ⅱ)若圆C与x轴交于A、B两点,点Q是圆C上异于A、B的任意一点,直线QA、QB分别交l:x=﹣4于R、S两点.当点Q变化时,以RS为直径的圆是否过圆C内的一定点,若过定点,请求出定点;若不过定点,请说明理由.
21.(15分)已知S={1,2,…,n},A S,T={t1,t2} S,记Ai={x|x=a+ti,a∈A}(i=1,2),用|X|表示有限集合X的元素个数.
(1)若n=4,A1 A2= ,分别讨论A={1,2,3}和A={1,2,4}时,集合T的情况;
(2)若n=6,A1 A2= ,求|A1∪A2|的最大值;
(3)若n=7,|A|=4,则对于任意的A,是否都存在T,使得A1 A2= ?说明理由.
参考答案
一、选择题:本大题共10道小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项符合题目的要求。把正确答案涂写在答题卡上相应的位置。
1.【分析】根据两点坐标求出直线AB的斜率即可.
【解答】解:直线AB的斜率k==2,
故选:A.
【点评】此题考查学生会根据两点坐标求过两点直线的斜率,是一道基础题.
2.【分析】由方程x2+y2﹣2x+4y+3=0可得(x﹣1)2+(y+2)2=2,即可得到圆心的坐标.
【解答】解:由方程x2+y2﹣2x+4y+3=0可得(x﹣1)2+(y+2)2=2,
∴圆心坐标为(1,﹣2).
故选:C.
【点评】本题考查了圆的标准方程及其配方法,属于基础题.
3.【分析】由题意可得:c=3,并且得到椭圆的焦点在x轴上,再根据椭圆的定义得到a=4,进而由a,b,c的关系求出b的值得到椭圆的方程.
【解答】解:∵两个焦点的坐标分别是(﹣3,0),(3,0),
∴椭圆的焦点在横轴上,并且c=3,
∴由椭圆的定义可得:2a=8,即a=4,
∴由a,b,c的关系解得b=,
∴椭圆方程是+=1.
故选:B.
【点评】本题主要考查椭圆的标准方程与椭圆的定义,以及考查椭圆的简单性质,此题属于基础题.
4.【分析】根据直线方程可求定点坐标.
【解答】解:由kx﹣y+1=3k得k(x﹣3)﹣y+1=0,所以直线过定点(3,1).
故选:C.
【点评】本题考查直线系方程求定点问题,考查学生的运算能力,属基础题.
5.【分析】根据题意,由圆的方程得到两个圆的圆心和半径,求出圆心距,再判断位置关系.
【解答】解:根据题意,圆C1:x2+y2=1,圆心为(0,0),半径r=1,
圆C2:x2+y2﹣8x+7=0,即(x﹣4)2+y2=9,圆心为(4,0),半径R=3,
圆心距|C1C2|=4=R+r,两圆外切.
故选:D.
【点评】本题考查圆与圆的位置关系,涉及圆的一般方程,属于基础题.
6.【分析】当直线l的斜率不存在时,直线l与圆有公共点;当直线l的斜率存在时,设直线l的方程为y﹣=k(x+),由直线l与圆有公共点,得到圆心(0,0)到直线的距离d小于等于圆半径,由此能求出直线l的倾斜角的取值范围.
【解答】解:当直线l的斜率不存在时,
直线l的方程为x=﹣,圆心(0,0)到直线的距离d=,
直线l与圆有公共点;
当直线l的斜率存在时,设直线l的方程为y﹣=k(x+),即kx﹣y++k=0,
∵直线l与圆有公共点,
∴圆心(0,0)到直线的距离d=≤,
解得k≤﹣,
∴直线l的倾斜角的取值范围是[,].
故选:A.
【点评】本题考查直线的倾斜角的取值范围的求法,考查圆、直线方程、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,属中档题.
7.【分析】由已知先求出两直线平行时的a,然后检验充分及必要性即可判断.
【解答】解:当直线l1:ax+4y﹣3=0与直线l2:x+(a﹣3)y+2=0”平行时,
有a(a﹣3)=4,
解得a=4或a=﹣1,经检验都符合题意,
故“a=﹣1”是“直线l1:ax+4y﹣3=0与直线l2:x+(a﹣3)y+2=0”平行的充分不必要条件.
故选:A.
【点评】本题主要考查了直线的一般式方程平行条件的应用,属于基础题.
8.【分析】由平面向量数量积的运算,结合平面向量线性运算求解即可.
【解答】解:由题意可得,,
又 ==,
故选:B.
【点评】本题考查了平面向量数量积的运算,重点考查了平面向量线性运算,属基础题.
9.【分析】由三角形的重心、垂心和外心的定义与性质,推出△ABC的欧拉线就是线段AB的中垂线,再求得中垂线的斜率和线段AB的中点,即可得解.
【解答】解:因为AC=BC,所以点C在线段AB的中垂线上,
设该中垂线为直线l,
取BC的中点D,连接AD,则AD与直线l的交点在直线l上,该交点即为△ABC的重心,
过点A作AE⊥BC于E,则AE与直线l的交点在直线l上,该交点即为△ABC的垂心,
因为外心到△ABC的三个顶点的距离相等,所以外心也在直线l上,
故△ABC的欧拉线就是直线l,
由A(2,0),B(1,2),知AB的中点坐标为(,1),直线AB的斜率为=﹣2,
所以直线l的斜率为,其方程为y﹣1=(x﹣),即2x﹣4y+1=0.
故选:D.
【点评】本题考查直线方程的求法,两条直线的垂直关系,理解三角形的重心、垂心和外心的定义与性质是解题的关键,考查逻辑推理能力和运算能力,属于中档题.
10.【分析】将方程中的x换成﹣x,y换成﹣y,即有﹣x3﹣y3=1,则x3+y3=﹣1,曲线C关于原点不对称;曲线C:x3+y3=1过点M(x,),M到原点O(0,0)的距离:|MO|=≥1;曲线C:x3+y3=1经过(1,0),(0,1)两个整数点.
【解答】解:将方程中的x换成﹣x,y换成﹣y,即有﹣x3﹣y3=1,则x3+y3=﹣1,
所以曲线C关于原点不对称,故①错误;
曲线C:x3+y3=1过点M(x,),
M到原点O(0,0)的距离:|MO|=≥1,故②正确;
曲线C:x3+y3=1经过(1,0),(0,1)两个整数点,故③正确;
故正确的结论的序号是:②③,
故选:C.
【点评】本题考查命题真假的判断,考查曲线的对称性、曲线上的点到原点的距离和整点问题等基础知识,考查运算求解能力,是中档题.
二、填空题:本大题共5小题,共25分。把答案填在答题纸中相应的横线上。
11.【分析】由垂直的性质求出x的值,从而可得的坐标,再由模的坐标运算即可求出||.
【解答】解:∵=(2,3,1),=(﹣4,2,x),且⊥,
∴ =﹣8+6+x=0,
解得x=2,
∴=(﹣4,2,2),
∴||==2.
故答案为:2.
【点评】本题考查向量的模的求法,考查向量垂直的性质等基础知识,考查运算求解能力,属于基础题.
12.【分析】由题意根据查直线的方向向量,求出直线的斜率,用点斜式求直线的方程,把 点A(a,b)代入直线l的方程,可得一组a,b的值.
【解答】解:∵过点(0,2)的直线l的方向向量为(1,6),
故直线l的斜率为6,方程为 y﹣2=6(x﹣0),即 y=6x+2.
∵点A(a,b)在直线l上,∴b=6a+2,
则满足条件的一组a,b的值依次为1,8.
【点评】本题主要考查直线的方向向量,用点斜式求直线的方程,属于基础题.
13.【分析】如图连接A1C1,取A1D1的中点F,连接EF,说明异面直线DE和AC所成角,就是异面直线DE和EF所成角,设正方体的棱长为:2,求出DE=DF,EF,即可求出cos∠DEF,得到所以异面直线DE和AC所成角的余弦值.
【解答】解:如图连接A1C1,取A1D1的中点F,连接EF,易知EF∥A1C1∥AC,
所以异面直线DE和AC所成角,就是异面直线DE和EF所成角,
设正方体的棱长为:2,
所以DE=DF==,
EF=,
所以cos∠DEF==,
所以异面直线DE和AC所成角的余弦值等于.
故答案为:.
【点评】本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.
14.【分析】先利用点斜式求出折线的方程,再利用“垂直、中点在轴上”这两个条件求得与点(﹣4,1)重合的点的坐标.
【解答】解:将一张坐标纸对折一次,已知点点(0,m)与点(m﹣2,2)重合,
则折线经过点(,),且斜率为=1,故折线的方程为y﹣=x﹣,即x﹣y+2=0.
则与点(﹣4,1)重合的点的坐标是M(a,b),则由,
解得a=﹣1,b=﹣2,
即M(﹣1,﹣2).
故答案为:(﹣1,﹣2).
【点评】本题主要考查求一个点关于某条直线的对称点的点的坐标的方法,利用了“垂直、中点在轴上”这两个条件,属于中档题.
15.【分析】根据题意,结合“叉乘运算”的定义,依次分析四个结论,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于①,|×|=||||sin90°=2×2×1=4,||=4,又由与、都垂直且三个向量构成右手系,则,①正确;
对于②,,而×=,②错误;
对于③,+=,则有|(+)×|=|×|=2×4×1=8,(+)×方向与相同,
|×|=2×4×1=8,×与方向相同,|×|=2×4×1=8,且×与方向相同,
故|×+×|=8,且×+×的方向与+即方向相同,
则有,③正确;
对于④,由于,则(×) = =4×4=16,V=2×2×4=16,④正确;
故答案为:①③④.
【点评】本题考查命题真假的判断,注意理解“叉乘运算”的定义以及运算性质,属于基础题.
三、解答题:本大题共6题,共85分。解答应写出文字说明、演算步骤或证明过程,并把答案写在答题纸中相应位置上。
16.【分析】(1)根据A(﹣3,9),B(2,2),C(5,3),求得点M的坐标,和直线直线BC的斜率,写出直线方程;
(2)根据,得到BC边的高线的斜率,写出直线方程.
【解答】解:(1)因为A(﹣3,9),B(2,2),C(5,3),
所以M(1,6),,
所以过M点和直线BC平行的直线方程为,
即x﹣3y+17=0;
(2)因为,
所以BC边的高线的斜率为﹣3,
所以BC边的高线所在直线方程y﹣9=﹣3(x+3),
即3x+y=0.
【点评】本题主要考查直线方程的求解,考查计算能力,属于基础题.
17.【分析】(1)通过证明四边形ABC1D1是平行四边形得出BC1∥AD1即可证明BC1∥平面AED1;
(2)以A为原点,建立空间直角坐标系,利用向量法能求出点A1到平面AED1的距离;
(3)利用向量法能求出直线AA1与平面AED1所成角的正弦值.
【解答】解:(1)证明:在棱长为2的正方体ABCD﹣A1B1C1D1中,E为线段BB1的中点,
∴AB∥C1D1,且AB=C1D1,
∴四边形ABC1D1是平行四边形,∴BC1∥AD1,
∵BC1 平面AED1,AD1 平面AED1,
∴BC1∥平面AED1;
(2)以A为原点,建立空间直角坐标系,如图,
则A1(0,0,2),A(0,0,0),D1(2,0,2),E(0,2,1),
则=(0,0,2),=(2,0,2),=(0,2,1),
设平面AED1的一个法向量为=(x,y,z),
则,取y=1,得=(2,1,﹣2),
则点A1到平面AED1的距离为:
d==;
(3)平面AED1的法向量为=(2,1,﹣2),
设直线AA1与平面AED1所成角为θ,
则直线AA1与平面AED1所成角的正弦值为:
sinθ===.
【点评】本题考查线面平行的判定与性质、线面角、点到平面的距离、向量法等基础知识,考查运算求解能力,是中档题.
18.【分析】(Ⅰ)设圆心坐标为C(a,b),半径为r.由已知可求a,b,r,进而可求圆C的方程;
(Ⅱ)选择条件①:求得圆心到直线的距离d=1,进而可求m的值.
选择条件②和③;可得d=,可求m的值.
【解答】解:(Ⅰ)设圆心坐标为C(a,b),半径为r.
由圆C的圆心在直线2x﹣y=0上,知:2a=b.
又∵圆C与x轴相切于点(1,0),
∴a=1,b=2,则r=|b﹣0|=2.
∴圆C圆心坐标为(1,2),则圆C的方程为(x﹣1)2+(y﹣2)2=4;
(Ⅱ)如果选择条件①:∠ACB=120°,而|CA|=|CB|=2,
∴圆心C到直线l的距离d=1,
以,
解得m=+1或m=﹣+1.
如果选择条件②; ,而|CA|=|CB|=2,
∴圆心C到直线l的距离,
则,
解得m=﹣1或3.
如果选择条件③;∠ACB=90°.而|CA|=|CB|=2,
∴圆心C到直线l的距离,
则,
解得m=﹣1或3.
【点评】本题考查直线与圆的位置关系,考查求圆的方程,考查点到线的距离,属中档题.
19.【分析】(Ⅰ)推导出BC⊥平面PAB. AE⊥BC. AE⊥PB.由此能证明AE⊥平面PBC.
(Ⅱ)建立空间直角坐标系A﹣xyz.利用向量法能求出m的值.
(Ⅲ)设F(0,0,t)(0≤t≤3).当m=2时,C(0,2,2).,.由PF⊥CE知,,﹣2﹣2t=0,t=﹣1.这与0≤t≤3矛盾.从而在线段AD上不存在点F,使得PF⊥CE.
【解答】解:(Ⅰ)证明:因为 AD⊥平面PAB,BC∥AD,
所以 BC⊥平面PAB.
又因为 AE 平面PAB,所以 AE⊥BC.
在△PAB中,PA=AB,E是PB的中点,所以 AE⊥PB.
又因为 BC∩PB=B,所以 AE⊥平面PBC.
(Ⅱ)解:因为 AD⊥平面PAB,所以AD⊥AB,AD⊥PA.
又因为 PA⊥AB,所以,如图建立空间直角坐标系A﹣xyz.
则A(0,0,0),B(0,2,0),C(0,2,m),E(1,1,0),P(2,0,0),D(0,0,3),
,.
设平面AEC的法向量为=(x,y,z).
则即 令x=1,则y=﹣1,,于是=(1,﹣1,).
因为AD⊥平面PAB,所以AD⊥PB.又PB⊥AE,所以PB⊥平面AED.
又因为,所以 取平面AED的法向量为=(﹣1,1,0).
所以|cos<>|==,即,解得m2=1.
又因为m>0,所以m=1.
(Ⅲ)解:结论:不存在.理由如下:
证明:设F(0,0,t)(0≤t≤3).
当m=2时,C(0,2,2).,.
由PF⊥CE知,,﹣2﹣2t=0,t=﹣1.这与0≤t≤3矛盾.
所以,在线段AD上不存在点F,使得PF⊥CE.
【点评】本题考查线面垂直的证明,考查实数值的求法,考查满足线线垂直的点是否存在的判断与证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
20.【分析】(Ⅰ)求得直线OP的方程,联立方程可得P的坐标,进而可求a,进而求得MN的长,求得C到直线y=﹣x﹣1的距离,可求△MON的面积;(Ⅱ)设直线QA的方程为y=k(x+3),其中k≠0,求得R的坐标,进而可得直线QB的方程,求得S的坐标,进而求得MN为直径的圆的方程,可求定点.
【解答】解:(Ⅰ)由题知:直线OP方程为,
则由,得到,即,
∵点P为线段MN的中点,∴MN⊥PC,
∴a=﹣2,∴,
∴C(﹣2,0)到直线y=﹣x﹣1距离为.
∴,
又:O到直线y=﹣x﹣1的距离为,MN边上的高为.
S△MON=××=;
(Ⅱ)不妨设直线QA的方程为 y=k(x+3),其中k≠0,
在直线QA的方程中,令x=﹣4,可得R(﹣4,﹣k),
因为QA⊥QB,则直线QB的方程为,
在直线QB的方程中,令x=﹣4,可得,即点,
线段EN的中点为,半径平方为,
所以以线段MN为直径的圆的方程为,
即,
由,解得,
因此,当点Q变化时,以RS为直径的圆恒过圆C内的定点.
【点评】本题考查直线与圆的综合运用,考查运算求解能力,属于中档题.
21.【分析】(1)由已知得t1﹣t2≠a﹣b,其中a,b∈A,当A={1,2,3}时,t1,t2相差3;由此可求得T,当A={1,2,4}时,同理可得;
(2)若n=6,A1 A2= ,S={1,2,3,4,5,6},当A={2,3,4,5,6}时,则t1,t2相差5,所以T={1,6},A中至多有5个元素,所以A1,A2也至多有5个元素,求出A1,A2得出结果.
(3)当A={1,2,5,7}时,2﹣1=1,5﹣1=4,5﹣2=3,7﹣1=6,7﹣2=5,7﹣5=2,则t1,t2相差不可能1,2,3,4,5,6,可得结论.
【解答】解:(1)若A1 A2= ,则t1﹣t2≠a﹣b,其中a,b∈A,
否则t1+a=t2+b,A1 A2≠ ,
若n=4,当A={1,2,3}时,2﹣1=1,3﹣1=2,
所以t1﹣t2≠1,2,则t1,t2相差3,
因为S={1,2,3,4},T={t1,t2} S,
所以T={1,4};
当A={1,2,4}时,2﹣1=1,4﹣2=2,4﹣1=3,
所以t1﹣t2≠1,2,3,
因为S={1,2,3,4},T={t1,t2} S,
所以T不存在;
(2)若n=6,A1 A2= ,S={1,2,3,4,5,6},
当A=S时,2﹣1=1,5﹣1=4,5﹣2=3,7﹣1=6,7﹣2=5,7﹣5=2,
所以A≠S,t1﹣t2≠1,2,3,4,5,所以T不存在;
所以A中至多有5个元素;
当A={2,3,4,5,6}时,3﹣2=1,4﹣2=2,5﹣2=3,6﹣2=4,
所以t1﹣t2≠1,2,3,4,则t1,t2相差5,
所以T={1,6};
Ai={x|x=a+ti,a∈A}(i=1,2),
所以A1={3,4,5,6,7},A2={8,9,10,11,12},A1 A2={3,4,5,6,7,8,9,10,11,12}.
因为A中至多有5个元素,所以A1,A2也至多有5个元素,
所以|A1∪A2|的最大值为10.
(3)不一定存在,
当A={1,2,5,7}时,
2﹣1=1,5﹣1=4,5﹣2=3,7﹣1=6,7﹣2=5,7﹣5=2,
则t1,t2相差不可能1,2,3,4,5,6,这与T={t1,t2} {1,2,3,4,5,6,7}矛盾,
故不都存在T.
【点评】本题考查元素与集合关系、集合中元素的性质、并集、交集运算等基础知识,考查运算求解能力,是难题.
数 学
一、选择题:本大题共10道小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项符合题目的要求。把正确答案涂写在答题卡上相应的位置。
1.已知A(﹣1,﹣3),B(3,5),则直线AB的斜率为( )
A.2 B.1 C. D.不存在
2.圆x2+y2﹣2x+4y+3=0的圆心坐标为( )
A.(﹣2,4) B.(2,﹣4) C.(1,﹣2) D.(﹣1,2)
3.两个焦点的坐标分别为(﹣3,0),(3,0)的椭圆上的任一点到两焦点的距离之和为8,则椭圆的标准方程
为( )
A.+=1 B.+=1
C.+=1 D.+=1
4.任意的k∈R,直线kx﹣y+1=3k恒过定点( )
A.(0,0) B.(0,1) C.(3,1) D.(2,1)
5.已知圆C1:x2+y2=1与圆C2:x2+y2﹣8x+7=0,则圆C1与圆C2的位置关系是( )
A.相离 B.相交 C.内切 D.外切
6.过点的直线l与圆有公共点,则直线l的倾斜角取值范围是( )
A. B. C. D.
7.“a=﹣1”是“直线l1:ax+4y﹣3=0与直线l2:x+(a﹣3)y+2=0”平行的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
8.如图,在平行六面体ABCD﹣A1B1C1D1中,AA1=AD=AB=2,∠BAD=,∠BAA1=∠A1AD=,则 =( )
A.12 B.8 C.6 D.4
9.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半.这条直线被后人称为三角形的欧拉线.已知△ABC的顶点A(2,0),B(1,2),且AC=BC,则△ABC的欧拉线的方程为( )
A.x﹣2y﹣4=0 B.2x+y﹣4=0 C.4x+2y+1=0 D.2x﹣4y+1=0
10.曲线C:x3+y3=1.给出下列结论:
①曲线C关于原点对称;
②曲线C上任意一点到原点的距离不小于1;
③曲线C只经过2个整点(即横、纵坐标均为整数的点).
其中,所有正确结论的序号是( )
A.①② B.② C.②③ D.③
二、填空题:本大题共5小题,共25分。把答案填在答题纸中相应的横线上。
11.(5分)已知空间向量=(2,3,1),=(﹣4,2,x),且⊥,则||= .
12.(5分)已知过点(0,2)的直线l的方向向量为(1,6),点A(a,b)在直线l上,则满足条件的一组a,b的值依次为 .
13.(5分)正方体中ABCD﹣A1B1C1D1,E是C1D1的中点,那么异面直线DE和AC所成角的余弦值等于 .
14.(5分)将一张坐标纸对折,如果点(0,m)与点(m﹣2,2)重合,则点(﹣4,1)与点 重合.
15.(5分)给定两个不共线的空间向量与,定义叉乘运算:.规定:
(ⅰ)为同时与,垂直的向量;
(ⅱ),,三个向量构成右手系(如图1);
(ⅲ).
如图2,在长方体ABCD﹣A1B1C1D1中,AB=AD=2,AA1=4.给出下列四个结论:
①;
②;
③;
④.
其中,正确结论的序号是 .
三、解答题:本大题共6题,共85分。解答应写出文字说明、演算步骤或证明过程,并把答案写在答题纸中相应位置上。
16.(14分)在平面直角坐标系中,已知A(﹣3,9),B(2,2),C(5,3),线段AC的中点M;
(1)求过M点和直线BC平行的直线方程;
(2)求BC边的高线所在直线方程.
17.(14分)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E为线段BB1的中点.
(1)求证:BC1∥平面AED1;
(2)求点A1到平面AED1的距离;
(3)直线AA1与平面AED1所成角的正弦值.
18.(14分)已知圆C的圆心在直线2x﹣y=0上,且与x轴相切于点(1,0).
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C直线l:x﹣y+m=0交于A,B两点,_____,求m的值.
从下列三个条件中任选一个补充在上面问题中并作答:
条件①:圆C被直线l分成两段圆弧,其弧长比为2:1;
条件②:;
条件③:∠ACB=90°.
19.(14分)如图,四棱锥P﹣ABCD中,AD⊥平面ABP,BC∥AD,∠PAB=90°.PA=AB=2,AD=3,BC=m,E是PB的中点.
(Ⅰ)证明:AE⊥平面PBC;
(Ⅱ)若二面角C﹣AE﹣D的余弦值是,求m的值;
(Ⅲ)若m=2,在线段AD上是否存在一点F,使得PF⊥CE.若存在,确定F点的位置;若不存在,说明理由.
20.(14分)已知圆C:(x﹣a)2+y2=1与直线y=﹣x﹣1交于M、N两点,点P为线段MN的中点,O为坐标原点,直线OP的斜率为.
(Ⅰ)求a的值及△MON的面积;
(Ⅱ)若圆C与x轴交于A、B两点,点Q是圆C上异于A、B的任意一点,直线QA、QB分别交l:x=﹣4于R、S两点.当点Q变化时,以RS为直径的圆是否过圆C内的一定点,若过定点,请求出定点;若不过定点,请说明理由.
21.(15分)已知S={1,2,…,n},A S,T={t1,t2} S,记Ai={x|x=a+ti,a∈A}(i=1,2),用|X|表示有限集合X的元素个数.
(1)若n=4,A1 A2= ,分别讨论A={1,2,3}和A={1,2,4}时,集合T的情况;
(2)若n=6,A1 A2= ,求|A1∪A2|的最大值;
(3)若n=7,|A|=4,则对于任意的A,是否都存在T,使得A1 A2= ?说明理由.
参考答案
一、选择题:本大题共10道小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项符合题目的要求。把正确答案涂写在答题卡上相应的位置。
1.【分析】根据两点坐标求出直线AB的斜率即可.
【解答】解:直线AB的斜率k==2,
故选:A.
【点评】此题考查学生会根据两点坐标求过两点直线的斜率,是一道基础题.
2.【分析】由方程x2+y2﹣2x+4y+3=0可得(x﹣1)2+(y+2)2=2,即可得到圆心的坐标.
【解答】解:由方程x2+y2﹣2x+4y+3=0可得(x﹣1)2+(y+2)2=2,
∴圆心坐标为(1,﹣2).
故选:C.
【点评】本题考查了圆的标准方程及其配方法,属于基础题.
3.【分析】由题意可得:c=3,并且得到椭圆的焦点在x轴上,再根据椭圆的定义得到a=4,进而由a,b,c的关系求出b的值得到椭圆的方程.
【解答】解:∵两个焦点的坐标分别是(﹣3,0),(3,0),
∴椭圆的焦点在横轴上,并且c=3,
∴由椭圆的定义可得:2a=8,即a=4,
∴由a,b,c的关系解得b=,
∴椭圆方程是+=1.
故选:B.
【点评】本题主要考查椭圆的标准方程与椭圆的定义,以及考查椭圆的简单性质,此题属于基础题.
4.【分析】根据直线方程可求定点坐标.
【解答】解:由kx﹣y+1=3k得k(x﹣3)﹣y+1=0,所以直线过定点(3,1).
故选:C.
【点评】本题考查直线系方程求定点问题,考查学生的运算能力,属基础题.
5.【分析】根据题意,由圆的方程得到两个圆的圆心和半径,求出圆心距,再判断位置关系.
【解答】解:根据题意,圆C1:x2+y2=1,圆心为(0,0),半径r=1,
圆C2:x2+y2﹣8x+7=0,即(x﹣4)2+y2=9,圆心为(4,0),半径R=3,
圆心距|C1C2|=4=R+r,两圆外切.
故选:D.
【点评】本题考查圆与圆的位置关系,涉及圆的一般方程,属于基础题.
6.【分析】当直线l的斜率不存在时,直线l与圆有公共点;当直线l的斜率存在时,设直线l的方程为y﹣=k(x+),由直线l与圆有公共点,得到圆心(0,0)到直线的距离d小于等于圆半径,由此能求出直线l的倾斜角的取值范围.
【解答】解:当直线l的斜率不存在时,
直线l的方程为x=﹣,圆心(0,0)到直线的距离d=,
直线l与圆有公共点;
当直线l的斜率存在时,设直线l的方程为y﹣=k(x+),即kx﹣y++k=0,
∵直线l与圆有公共点,
∴圆心(0,0)到直线的距离d=≤,
解得k≤﹣,
∴直线l的倾斜角的取值范围是[,].
故选:A.
【点评】本题考查直线的倾斜角的取值范围的求法,考查圆、直线方程、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,属中档题.
7.【分析】由已知先求出两直线平行时的a,然后检验充分及必要性即可判断.
【解答】解:当直线l1:ax+4y﹣3=0与直线l2:x+(a﹣3)y+2=0”平行时,
有a(a﹣3)=4,
解得a=4或a=﹣1,经检验都符合题意,
故“a=﹣1”是“直线l1:ax+4y﹣3=0与直线l2:x+(a﹣3)y+2=0”平行的充分不必要条件.
故选:A.
【点评】本题主要考查了直线的一般式方程平行条件的应用,属于基础题.
8.【分析】由平面向量数量积的运算,结合平面向量线性运算求解即可.
【解答】解:由题意可得,,
又 ==,
故选:B.
【点评】本题考查了平面向量数量积的运算,重点考查了平面向量线性运算,属基础题.
9.【分析】由三角形的重心、垂心和外心的定义与性质,推出△ABC的欧拉线就是线段AB的中垂线,再求得中垂线的斜率和线段AB的中点,即可得解.
【解答】解:因为AC=BC,所以点C在线段AB的中垂线上,
设该中垂线为直线l,
取BC的中点D,连接AD,则AD与直线l的交点在直线l上,该交点即为△ABC的重心,
过点A作AE⊥BC于E,则AE与直线l的交点在直线l上,该交点即为△ABC的垂心,
因为外心到△ABC的三个顶点的距离相等,所以外心也在直线l上,
故△ABC的欧拉线就是直线l,
由A(2,0),B(1,2),知AB的中点坐标为(,1),直线AB的斜率为=﹣2,
所以直线l的斜率为,其方程为y﹣1=(x﹣),即2x﹣4y+1=0.
故选:D.
【点评】本题考查直线方程的求法,两条直线的垂直关系,理解三角形的重心、垂心和外心的定义与性质是解题的关键,考查逻辑推理能力和运算能力,属于中档题.
10.【分析】将方程中的x换成﹣x,y换成﹣y,即有﹣x3﹣y3=1,则x3+y3=﹣1,曲线C关于原点不对称;曲线C:x3+y3=1过点M(x,),M到原点O(0,0)的距离:|MO|=≥1;曲线C:x3+y3=1经过(1,0),(0,1)两个整数点.
【解答】解:将方程中的x换成﹣x,y换成﹣y,即有﹣x3﹣y3=1,则x3+y3=﹣1,
所以曲线C关于原点不对称,故①错误;
曲线C:x3+y3=1过点M(x,),
M到原点O(0,0)的距离:|MO|=≥1,故②正确;
曲线C:x3+y3=1经过(1,0),(0,1)两个整数点,故③正确;
故正确的结论的序号是:②③,
故选:C.
【点评】本题考查命题真假的判断,考查曲线的对称性、曲线上的点到原点的距离和整点问题等基础知识,考查运算求解能力,是中档题.
二、填空题:本大题共5小题,共25分。把答案填在答题纸中相应的横线上。
11.【分析】由垂直的性质求出x的值,从而可得的坐标,再由模的坐标运算即可求出||.
【解答】解:∵=(2,3,1),=(﹣4,2,x),且⊥,
∴ =﹣8+6+x=0,
解得x=2,
∴=(﹣4,2,2),
∴||==2.
故答案为:2.
【点评】本题考查向量的模的求法,考查向量垂直的性质等基础知识,考查运算求解能力,属于基础题.
12.【分析】由题意根据查直线的方向向量,求出直线的斜率,用点斜式求直线的方程,把 点A(a,b)代入直线l的方程,可得一组a,b的值.
【解答】解:∵过点(0,2)的直线l的方向向量为(1,6),
故直线l的斜率为6,方程为 y﹣2=6(x﹣0),即 y=6x+2.
∵点A(a,b)在直线l上,∴b=6a+2,
则满足条件的一组a,b的值依次为1,8.
【点评】本题主要考查直线的方向向量,用点斜式求直线的方程,属于基础题.
13.【分析】如图连接A1C1,取A1D1的中点F,连接EF,说明异面直线DE和AC所成角,就是异面直线DE和EF所成角,设正方体的棱长为:2,求出DE=DF,EF,即可求出cos∠DEF,得到所以异面直线DE和AC所成角的余弦值.
【解答】解:如图连接A1C1,取A1D1的中点F,连接EF,易知EF∥A1C1∥AC,
所以异面直线DE和AC所成角,就是异面直线DE和EF所成角,
设正方体的棱长为:2,
所以DE=DF==,
EF=,
所以cos∠DEF==,
所以异面直线DE和AC所成角的余弦值等于.
故答案为:.
【点评】本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.
14.【分析】先利用点斜式求出折线的方程,再利用“垂直、中点在轴上”这两个条件求得与点(﹣4,1)重合的点的坐标.
【解答】解:将一张坐标纸对折一次,已知点点(0,m)与点(m﹣2,2)重合,
则折线经过点(,),且斜率为=1,故折线的方程为y﹣=x﹣,即x﹣y+2=0.
则与点(﹣4,1)重合的点的坐标是M(a,b),则由,
解得a=﹣1,b=﹣2,
即M(﹣1,﹣2).
故答案为:(﹣1,﹣2).
【点评】本题主要考查求一个点关于某条直线的对称点的点的坐标的方法,利用了“垂直、中点在轴上”这两个条件,属于中档题.
15.【分析】根据题意,结合“叉乘运算”的定义,依次分析四个结论,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于①,|×|=||||sin90°=2×2×1=4,||=4,又由与、都垂直且三个向量构成右手系,则,①正确;
对于②,,而×=,②错误;
对于③,+=,则有|(+)×|=|×|=2×4×1=8,(+)×方向与相同,
|×|=2×4×1=8,×与方向相同,|×|=2×4×1=8,且×与方向相同,
故|×+×|=8,且×+×的方向与+即方向相同,
则有,③正确;
对于④,由于,则(×) = =4×4=16,V=2×2×4=16,④正确;
故答案为:①③④.
【点评】本题考查命题真假的判断,注意理解“叉乘运算”的定义以及运算性质,属于基础题.
三、解答题:本大题共6题,共85分。解答应写出文字说明、演算步骤或证明过程,并把答案写在答题纸中相应位置上。
16.【分析】(1)根据A(﹣3,9),B(2,2),C(5,3),求得点M的坐标,和直线直线BC的斜率,写出直线方程;
(2)根据,得到BC边的高线的斜率,写出直线方程.
【解答】解:(1)因为A(﹣3,9),B(2,2),C(5,3),
所以M(1,6),,
所以过M点和直线BC平行的直线方程为,
即x﹣3y+17=0;
(2)因为,
所以BC边的高线的斜率为﹣3,
所以BC边的高线所在直线方程y﹣9=﹣3(x+3),
即3x+y=0.
【点评】本题主要考查直线方程的求解,考查计算能力,属于基础题.
17.【分析】(1)通过证明四边形ABC1D1是平行四边形得出BC1∥AD1即可证明BC1∥平面AED1;
(2)以A为原点,建立空间直角坐标系,利用向量法能求出点A1到平面AED1的距离;
(3)利用向量法能求出直线AA1与平面AED1所成角的正弦值.
【解答】解:(1)证明:在棱长为2的正方体ABCD﹣A1B1C1D1中,E为线段BB1的中点,
∴AB∥C1D1,且AB=C1D1,
∴四边形ABC1D1是平行四边形,∴BC1∥AD1,
∵BC1 平面AED1,AD1 平面AED1,
∴BC1∥平面AED1;
(2)以A为原点,建立空间直角坐标系,如图,
则A1(0,0,2),A(0,0,0),D1(2,0,2),E(0,2,1),
则=(0,0,2),=(2,0,2),=(0,2,1),
设平面AED1的一个法向量为=(x,y,z),
则,取y=1,得=(2,1,﹣2),
则点A1到平面AED1的距离为:
d==;
(3)平面AED1的法向量为=(2,1,﹣2),
设直线AA1与平面AED1所成角为θ,
则直线AA1与平面AED1所成角的正弦值为:
sinθ===.
【点评】本题考查线面平行的判定与性质、线面角、点到平面的距离、向量法等基础知识,考查运算求解能力,是中档题.
18.【分析】(Ⅰ)设圆心坐标为C(a,b),半径为r.由已知可求a,b,r,进而可求圆C的方程;
(Ⅱ)选择条件①:求得圆心到直线的距离d=1,进而可求m的值.
选择条件②和③;可得d=,可求m的值.
【解答】解:(Ⅰ)设圆心坐标为C(a,b),半径为r.
由圆C的圆心在直线2x﹣y=0上,知:2a=b.
又∵圆C与x轴相切于点(1,0),
∴a=1,b=2,则r=|b﹣0|=2.
∴圆C圆心坐标为(1,2),则圆C的方程为(x﹣1)2+(y﹣2)2=4;
(Ⅱ)如果选择条件①:∠ACB=120°,而|CA|=|CB|=2,
∴圆心C到直线l的距离d=1,
以,
解得m=+1或m=﹣+1.
如果选择条件②; ,而|CA|=|CB|=2,
∴圆心C到直线l的距离,
则,
解得m=﹣1或3.
如果选择条件③;∠ACB=90°.而|CA|=|CB|=2,
∴圆心C到直线l的距离,
则,
解得m=﹣1或3.
【点评】本题考查直线与圆的位置关系,考查求圆的方程,考查点到线的距离,属中档题.
19.【分析】(Ⅰ)推导出BC⊥平面PAB. AE⊥BC. AE⊥PB.由此能证明AE⊥平面PBC.
(Ⅱ)建立空间直角坐标系A﹣xyz.利用向量法能求出m的值.
(Ⅲ)设F(0,0,t)(0≤t≤3).当m=2时,C(0,2,2).,.由PF⊥CE知,,﹣2﹣2t=0,t=﹣1.这与0≤t≤3矛盾.从而在线段AD上不存在点F,使得PF⊥CE.
【解答】解:(Ⅰ)证明:因为 AD⊥平面PAB,BC∥AD,
所以 BC⊥平面PAB.
又因为 AE 平面PAB,所以 AE⊥BC.
在△PAB中,PA=AB,E是PB的中点,所以 AE⊥PB.
又因为 BC∩PB=B,所以 AE⊥平面PBC.
(Ⅱ)解:因为 AD⊥平面PAB,所以AD⊥AB,AD⊥PA.
又因为 PA⊥AB,所以,如图建立空间直角坐标系A﹣xyz.
则A(0,0,0),B(0,2,0),C(0,2,m),E(1,1,0),P(2,0,0),D(0,0,3),
,.
设平面AEC的法向量为=(x,y,z).
则即 令x=1,则y=﹣1,,于是=(1,﹣1,).
因为AD⊥平面PAB,所以AD⊥PB.又PB⊥AE,所以PB⊥平面AED.
又因为,所以 取平面AED的法向量为=(﹣1,1,0).
所以|cos<>|==,即,解得m2=1.
又因为m>0,所以m=1.
(Ⅲ)解:结论:不存在.理由如下:
证明:设F(0,0,t)(0≤t≤3).
当m=2时,C(0,2,2).,.
由PF⊥CE知,,﹣2﹣2t=0,t=﹣1.这与0≤t≤3矛盾.
所以,在线段AD上不存在点F,使得PF⊥CE.
【点评】本题考查线面垂直的证明,考查实数值的求法,考查满足线线垂直的点是否存在的判断与证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
20.【分析】(Ⅰ)求得直线OP的方程,联立方程可得P的坐标,进而可求a,进而求得MN的长,求得C到直线y=﹣x﹣1的距离,可求△MON的面积;(Ⅱ)设直线QA的方程为y=k(x+3),其中k≠0,求得R的坐标,进而可得直线QB的方程,求得S的坐标,进而求得MN为直径的圆的方程,可求定点.
【解答】解:(Ⅰ)由题知:直线OP方程为,
则由,得到,即,
∵点P为线段MN的中点,∴MN⊥PC,
∴a=﹣2,∴,
∴C(﹣2,0)到直线y=﹣x﹣1距离为.
∴,
又:O到直线y=﹣x﹣1的距离为,MN边上的高为.
S△MON=××=;
(Ⅱ)不妨设直线QA的方程为 y=k(x+3),其中k≠0,
在直线QA的方程中,令x=﹣4,可得R(﹣4,﹣k),
因为QA⊥QB,则直线QB的方程为,
在直线QB的方程中,令x=﹣4,可得,即点,
线段EN的中点为,半径平方为,
所以以线段MN为直径的圆的方程为,
即,
由,解得,
因此,当点Q变化时,以RS为直径的圆恒过圆C内的定点.
【点评】本题考查直线与圆的综合运用,考查运算求解能力,属于中档题.
21.【分析】(1)由已知得t1﹣t2≠a﹣b,其中a,b∈A,当A={1,2,3}时,t1,t2相差3;由此可求得T,当A={1,2,4}时,同理可得;
(2)若n=6,A1 A2= ,S={1,2,3,4,5,6},当A={2,3,4,5,6}时,则t1,t2相差5,所以T={1,6},A中至多有5个元素,所以A1,A2也至多有5个元素,求出A1,A2得出结果.
(3)当A={1,2,5,7}时,2﹣1=1,5﹣1=4,5﹣2=3,7﹣1=6,7﹣2=5,7﹣5=2,则t1,t2相差不可能1,2,3,4,5,6,可得结论.
【解答】解:(1)若A1 A2= ,则t1﹣t2≠a﹣b,其中a,b∈A,
否则t1+a=t2+b,A1 A2≠ ,
若n=4,当A={1,2,3}时,2﹣1=1,3﹣1=2,
所以t1﹣t2≠1,2,则t1,t2相差3,
因为S={1,2,3,4},T={t1,t2} S,
所以T={1,4};
当A={1,2,4}时,2﹣1=1,4﹣2=2,4﹣1=3,
所以t1﹣t2≠1,2,3,
因为S={1,2,3,4},T={t1,t2} S,
所以T不存在;
(2)若n=6,A1 A2= ,S={1,2,3,4,5,6},
当A=S时,2﹣1=1,5﹣1=4,5﹣2=3,7﹣1=6,7﹣2=5,7﹣5=2,
所以A≠S,t1﹣t2≠1,2,3,4,5,所以T不存在;
所以A中至多有5个元素;
当A={2,3,4,5,6}时,3﹣2=1,4﹣2=2,5﹣2=3,6﹣2=4,
所以t1﹣t2≠1,2,3,4,则t1,t2相差5,
所以T={1,6};
Ai={x|x=a+ti,a∈A}(i=1,2),
所以A1={3,4,5,6,7},A2={8,9,10,11,12},A1 A2={3,4,5,6,7,8,9,10,11,12}.
因为A中至多有5个元素,所以A1,A2也至多有5个元素,
所以|A1∪A2|的最大值为10.
(3)不一定存在,
当A={1,2,5,7}时,
2﹣1=1,5﹣1=4,5﹣2=3,7﹣1=6,7﹣2=5,7﹣5=2,
则t1,t2相差不可能1,2,3,4,5,6,这与T={t1,t2} {1,2,3,4,5,6,7}矛盾,
故不都存在T.
【点评】本题考查元素与集合关系、集合中元素的性质、并集、交集运算等基础知识,考查运算求解能力,是难题.
同课章节目录
