江苏省苏州市昆山通海实验中学2023-2024学年八年级上学期12月单元练习数学试卷(PDF版无答案)
文档属性
| 名称 | 江苏省苏州市昆山通海实验中学2023-2024学年八年级上学期12月单元练习数学试卷(PDF版无答案) | 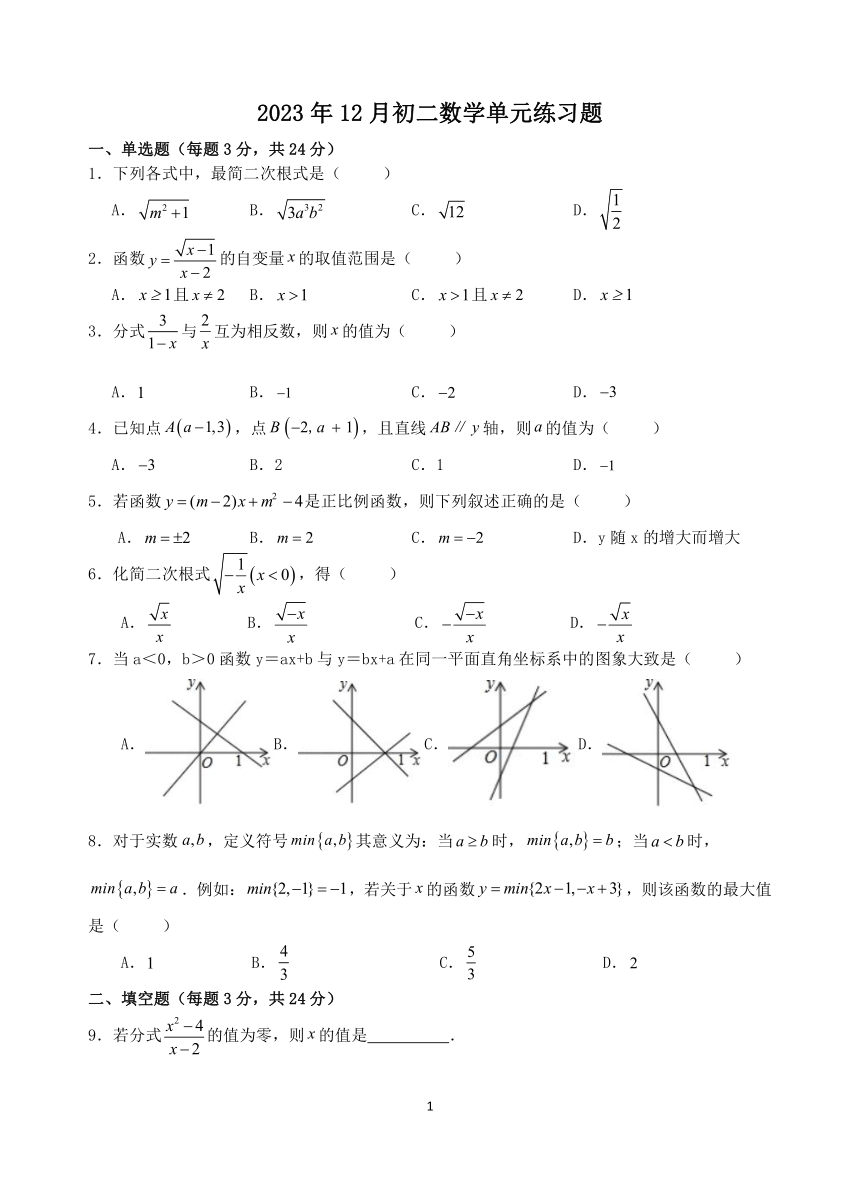 | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:52:09 | ||
图片预览

文档简介
2023 年 12 月初二数学单元练习题
一、单选题(每题 3 分,共 24 分)
1.下列各式中,最简二次根式是( )
1
A. m2 1 B. 3a3b2 C. 12 D. 2
y x 12.函数 的自变量 x的取值范围是( )
x 2
A. x 1且 x 2 B. x 1 C. x 1且 x 2 D. x 1
3 2
3.分式 与 互为相反数,则 x的值为( )
1 x x
A.1 B. 1 C. 2 D. 3
4.已知点 A a 1,3 ,点 B 2,a 1 ,且直线 AB∥ y轴,则 a的值为( )
A. 3 B.2 C.1 D. 1
5.若函数 y (m 2)x m2 4是正比例函数,则下列叙述正确的是( )
A.m 2 B.m 2 C.m 2 D.y 随 x 的增大而增大
1
6.化简二次根式 x 0 ,得( )
x
x x x x
A. B. C. D.
x x x x
7.当 a<0,b>0函数 y=ax+b 与 y=bx+a 在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
8.对于实数 a,b,定义符号min a,b 其意义为:当 a b时,min a,b b;当 a b时,
min a,b a.例如:min{2, 1} 1,若关于 x的函数 y min{2x 1, x 3},则该函数的最大值
是( )
4 5
A.1 B. C. D. 2
3 3
二、填空题(每题 3 分,共 24 分)
x2 4
9.若分式 的值为零,则 x的值是 .
x 2
1
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
10.直线 y 3x b与 y轴交点 0, 2 ,则这条直线不经过第 象限.
11.已知点 A 2,3 ,将点A绕原点O逆时针方向旋转90 得点 B,则点 B的坐标为 .
2x m
12.已知关于 x 的方程 3的解是非负数,则 m 的取值范围为 .
x 2
13.在平面直角坐标系中,A 3,0 ,B 0,4 ,若以 AB为腰作等腰三角形 ABC,则在 x轴上满足
条件的点C坐标是 .
14
1 1
14.如图,直线 y= kx b与 y= x 交于 A(3,1)与 x 轴交于 B(6,0),则不等式组 0 kx b x
3 3
的解集为 .
15.如图,AB BC,DC BC,垂足分别为 B,C, BAD和 ADC的平分线与 BC相交于点 E,
AD 8.BC 6,则四边形 ABCD的面积为 . .
16.甲、乙两车从 A 地出发,匀速驶向 B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路
线行驶.乙车先到达 B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两
车之间的距离 y km 与乙车行驶时间 x h 之间的函数关系如图所示,给出下列说法:①乙车的速
度是120km/h ;②m 160;③点 H 的坐标是 7,80 ;④n 7.5.其中说法正确的有 .
二、解答题(每题 3 分,共 82 分)
17(6 分).解方程
2 1 x 1 2 3 x 3(1) ; (2) 2 .x 2 2 x x 1 x 1 x 1
2 2
18.(6 分)计算(1)2 5 4 ( 4) ; (2) 45 75 1 9 527
2a 2a 4 a 2
19(6 分).先化简,再求值: ,其中 ;
a 1 a 2 1 a 2 2a 1 a 2 1
2 mx 3
20(8 分).关于 x的分式方程 x 2 x 1 x 2 x 1.
(1)若方程的增根为 x 2,求 m 的值; (2)若方程无解,求 m 的值.
2
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
21.(6 分)已知 y 4与 x 3成正比例,且 x 1时, y 0
(1)求 y 与 x 的函数表达式; (2)点M (m 1, 2m)在该函数图象上,求点 M 的坐标.
22.(8 分)如图,在平面直角坐标系中, A 3,2 ,B 4, 3 , C 1, 1 .
(1)在图中作出 ABC关于 y轴对称的△A1B1C1;
(2)写出点C1的坐标 (直接写答案 ):C1______
(3)△A1B1C1的面积为______;
(4)在 y轴上画出点 P,使 PB PC最小.
23.(6 分)已知直线 y = kx + b(k ≠ 0)经过点 A(3,0),B(1,2)
(1)求直线 y = kx + b的函数表达式;
(2)若直线 y = x 2与直线 y = kx + b相交于点 C,求点 C的坐标;
24.(8分)某中学有一块四边形的空地 ,如图所示,学校计划在空地上种植草皮,经测量∠ =
90°, = 3 , = 4 , = 12 , = 13 .若每平方米草皮需要 200 元,问学校需要投入
多少资金买草皮?
25.(8 分)甲车从 A 地出发匀速向 B地行驶,同时乙车从 B地出发匀速向 A 地行驶,甲车行驶速
度比乙车快,甲、乙两车距 A 地的路程 y(千米)与行驶时间 x (小时)之间的关系如下图所示,请
结合图像回答下列问题:
(1)甲车速度为 km/h,乙车速度为 km/h;
(2)求乙车行驶过程中,y 与 x的函数关系式;
(3)在行驶过程中,两车出发多长时间,两车相距80千米?
3
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
26.(10 分)某家电销售商城电冰箱的销售价为每台 2100 元,空调的销售价为每台 1750 元,每
台电冰箱的进价比每台空调的进价多 400 元,商城用 80000 元购进电冰箱的数量与用 64000 元购
进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少;
(2)现在商城准备一次购进这两种家电共 100 台,设购进电冰箱 x 台,这 100 台家电的销售总利
润为 y 元,要求购进空调数量不超过电冰箱数量的 2倍,总利润不低于 13200 元,请分析合理的
方案共有多少种,并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调 k(0 k 100)元,若商店保持这两种家电的售价不
变,请你根据以上信息及(2)问中条件,设计出使这 100 台家电销售总利润最大的进货方案.
1
27.(10 分)如图,直线 l1 : y x 2与 x轴交于点 A,与 y 轴交于点 B,直线 l2与 x轴交于点 C,3
与 y轴交于 D点, AC 8, OD 3OC.
(1)求直线CD的解析式;
3
(2)点 Q 为直线 AB上一动点,若有 S QCD S OAB,请求出 Q 点坐标;2
(3)点 M 为直线 AB上一动点,点 N为 y轴上一动点,是否存在以点 M, N, C为顶点且以MN为
直角边的三角形是等腰直角三角形,若存在,请直接写出点 M 的坐标,若不存在,请说明理由.
4
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
一、单选题(每题 3 分,共 24 分)
1.下列各式中,最简二次根式是( )
1
A. m2 1 B. 3a3b2 C. 12 D. 2
y x 12.函数 的自变量 x的取值范围是( )
x 2
A. x 1且 x 2 B. x 1 C. x 1且 x 2 D. x 1
3 2
3.分式 与 互为相反数,则 x的值为( )
1 x x
A.1 B. 1 C. 2 D. 3
4.已知点 A a 1,3 ,点 B 2,a 1 ,且直线 AB∥ y轴,则 a的值为( )
A. 3 B.2 C.1 D. 1
5.若函数 y (m 2)x m2 4是正比例函数,则下列叙述正确的是( )
A.m 2 B.m 2 C.m 2 D.y 随 x 的增大而增大
1
6.化简二次根式 x 0 ,得( )
x
x x x x
A. B. C. D.
x x x x
7.当 a<0,b>0函数 y=ax+b 与 y=bx+a 在同一平面直角坐标系中的图象大致是( )
A. B. C. D.
8.对于实数 a,b,定义符号min a,b 其意义为:当 a b时,min a,b b;当 a b时,
min a,b a.例如:min{2, 1} 1,若关于 x的函数 y min{2x 1, x 3},则该函数的最大值
是( )
4 5
A.1 B. C. D. 2
3 3
二、填空题(每题 3 分,共 24 分)
x2 4
9.若分式 的值为零,则 x的值是 .
x 2
1
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
10.直线 y 3x b与 y轴交点 0, 2 ,则这条直线不经过第 象限.
11.已知点 A 2,3 ,将点A绕原点O逆时针方向旋转90 得点 B,则点 B的坐标为 .
2x m
12.已知关于 x 的方程 3的解是非负数,则 m 的取值范围为 .
x 2
13.在平面直角坐标系中,A 3,0 ,B 0,4 ,若以 AB为腰作等腰三角形 ABC,则在 x轴上满足
条件的点C坐标是 .
14
1 1
14.如图,直线 y= kx b与 y= x 交于 A(3,1)与 x 轴交于 B(6,0),则不等式组 0 kx b x
3 3
的解集为 .
15.如图,AB BC,DC BC,垂足分别为 B,C, BAD和 ADC的平分线与 BC相交于点 E,
AD 8.BC 6,则四边形 ABCD的面积为 . .
16.甲、乙两车从 A 地出发,匀速驶向 B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路
线行驶.乙车先到达 B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两
车之间的距离 y km 与乙车行驶时间 x h 之间的函数关系如图所示,给出下列说法:①乙车的速
度是120km/h ;②m 160;③点 H 的坐标是 7,80 ;④n 7.5.其中说法正确的有 .
二、解答题(每题 3 分,共 82 分)
17(6 分).解方程
2 1 x 1 2 3 x 3(1) ; (2) 2 .x 2 2 x x 1 x 1 x 1
2 2
18.(6 分)计算(1)2 5 4 ( 4) ; (2) 45 75 1 9 527
2a 2a 4 a 2
19(6 分).先化简,再求值: ,其中 ;
a 1 a 2 1 a 2 2a 1 a 2 1
2 mx 3
20(8 分).关于 x的分式方程 x 2 x 1 x 2 x 1.
(1)若方程的增根为 x 2,求 m 的值; (2)若方程无解,求 m 的值.
2
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
21.(6 分)已知 y 4与 x 3成正比例,且 x 1时, y 0
(1)求 y 与 x 的函数表达式; (2)点M (m 1, 2m)在该函数图象上,求点 M 的坐标.
22.(8 分)如图,在平面直角坐标系中, A 3,2 ,B 4, 3 , C 1, 1 .
(1)在图中作出 ABC关于 y轴对称的△A1B1C1;
(2)写出点C1的坐标 (直接写答案 ):C1______
(3)△A1B1C1的面积为______;
(4)在 y轴上画出点 P,使 PB PC最小.
23.(6 分)已知直线 y = kx + b(k ≠ 0)经过点 A(3,0),B(1,2)
(1)求直线 y = kx + b的函数表达式;
(2)若直线 y = x 2与直线 y = kx + b相交于点 C,求点 C的坐标;
24.(8分)某中学有一块四边形的空地 ,如图所示,学校计划在空地上种植草皮,经测量∠ =
90°, = 3 , = 4 , = 12 , = 13 .若每平方米草皮需要 200 元,问学校需要投入
多少资金买草皮?
25.(8 分)甲车从 A 地出发匀速向 B地行驶,同时乙车从 B地出发匀速向 A 地行驶,甲车行驶速
度比乙车快,甲、乙两车距 A 地的路程 y(千米)与行驶时间 x (小时)之间的关系如下图所示,请
结合图像回答下列问题:
(1)甲车速度为 km/h,乙车速度为 km/h;
(2)求乙车行驶过程中,y 与 x的函数关系式;
(3)在行驶过程中,两车出发多长时间,两车相距80千米?
3
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
26.(10 分)某家电销售商城电冰箱的销售价为每台 2100 元,空调的销售价为每台 1750 元,每
台电冰箱的进价比每台空调的进价多 400 元,商城用 80000 元购进电冰箱的数量与用 64000 元购
进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少;
(2)现在商城准备一次购进这两种家电共 100 台,设购进电冰箱 x 台,这 100 台家电的销售总利
润为 y 元,要求购进空调数量不超过电冰箱数量的 2倍,总利润不低于 13200 元,请分析合理的
方案共有多少种,并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调 k(0 k 100)元,若商店保持这两种家电的售价不
变,请你根据以上信息及(2)问中条件,设计出使这 100 台家电销售总利润最大的进货方案.
1
27.(10 分)如图,直线 l1 : y x 2与 x轴交于点 A,与 y 轴交于点 B,直线 l2与 x轴交于点 C,3
与 y轴交于 D点, AC 8, OD 3OC.
(1)求直线CD的解析式;
3
(2)点 Q 为直线 AB上一动点,若有 S QCD S OAB,请求出 Q 点坐标;2
(3)点 M 为直线 AB上一动点,点 N为 y轴上一动点,是否存在以点 M, N, C为顶点且以MN为
直角边的三角形是等腰直角三角形,若存在,请直接写出点 M 的坐标,若不存在,请说明理由.
4
{#{QQABLYAUogCAAAIAABgCQQHYCAOQkBCCCAoGxBAMMAABwRNABAA=}#}
同课章节目录
