28.2 解直角三角形(4)
文档属性
| 名称 | 28.2 解直角三角形(4) |

|
|
| 格式 | rar | ||
| 文件大小 | 647.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-09 00:00:00 | ||
图片预览




文档简介
课件17张PPT。28.2 解直角三角形(4)探索新知坡度通常写成1∶m的形式,如i=1∶.坡面与水平面的夹角叫做坡角,记作a,有i= =tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即i= .
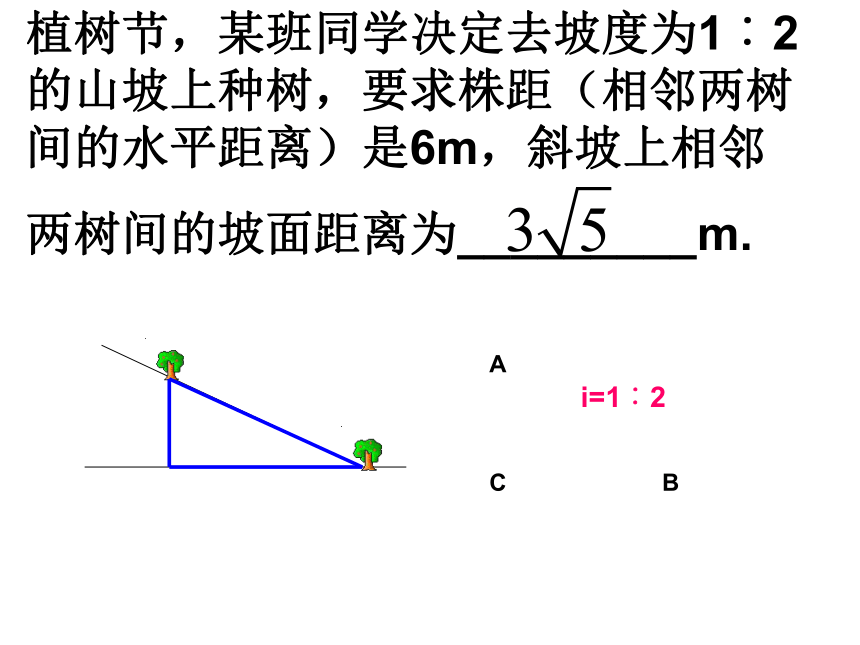
植树节,某班同学决定去坡度为1︰2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,斜坡上相邻
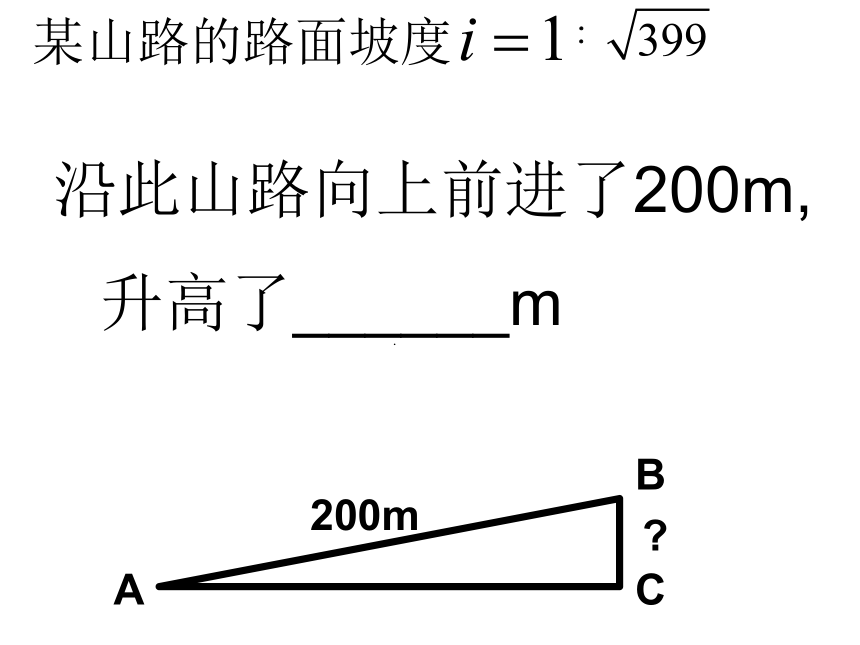
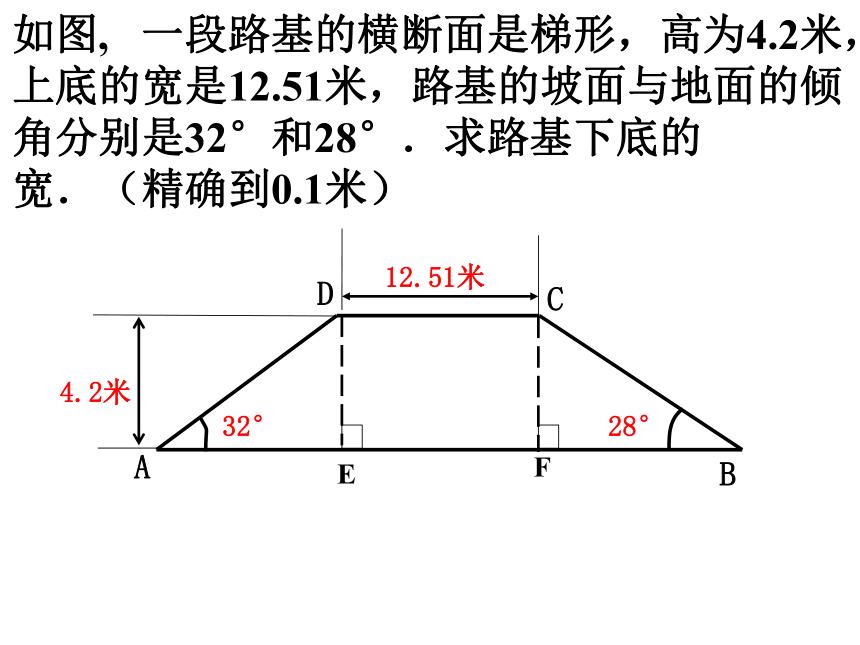
两树间的坡面距离为_________m.ACBi=1︰2某山路的路面坡度 ︰ 沿此山路向上前进了200m, 升高了______m. ABC200m?如图, 一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到0.1米) 利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分),已知渠道内坡度为1∶1.5,渠道底面宽BC为0.5米,求:
①横断面(等腰梯形)ABCD的面积;
②修一条长为100米的渠道要挖去的土方数. ∴AE=1.5×0.6=0.9(米).
∵等腰梯形ABCD,
∴FD=AE=0.9(米).
∴AD=2×0.9+0.5=2.3(米).
总土方数=截面积×渠长
=0.8×100=80(米3).
答:横断面ABCD面积为0.8平方米,修一条长为100米的渠道要挖出的土方数为80立方米.
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l化整为零,积零为整,化曲为直,以直代曲的解决问题的策略与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢? 我们设法“化曲为直,以直代曲”. 我们可以把山坡“化整为零”地划分为一些小段,图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度h1=l1sina1. 在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h. 以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容. 利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.)锥角
显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即i= .
植树节,某班同学决定去坡度为1︰2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,斜坡上相邻
两树间的坡面距离为_________m.ACBi=1︰2某山路的路面坡度 ︰ 沿此山路向上前进了200m, 升高了______m. ABC200m?如图, 一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°和28°.求路基下底的宽.(精确到0.1米) 利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分),已知渠道内坡度为1∶1.5,渠道底面宽BC为0.5米,求:
①横断面(等腰梯形)ABCD的面积;
②修一条长为100米的渠道要挖去的土方数. ∴AE=1.5×0.6=0.9(米).
∵等腰梯形ABCD,
∴FD=AE=0.9(米).
∴AD=2×0.9+0.5=2.3(米).
总土方数=截面积×渠长
=0.8×100=80(米3).
答:横断面ABCD面积为0.8平方米,修一条长为100米的渠道要挖出的土方数为80立方米.
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l化整为零,积零为整,化曲为直,以直代曲的解决问题的策略与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢? 我们设法“化曲为直,以直代曲”. 我们可以把山坡“化整为零”地划分为一些小段,图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度h1=l1sina1. 在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h. 以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容. 利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.)锥角
