2024年九年级中考数学压轴题锦囊妙计—规律探究专题
文档属性
| 名称 | 2024年九年级中考数学压轴题锦囊妙计—规律探究专题 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-07 17:05:20 | ||
图片预览



文档简介
规律探究专题
初中数学的知识内容大致可以分为代数和几何两类,这个分类对于规律探究题同样适用,中考在考查时只是做了进一步的细化,例如以数为基础进一步衍生出数式类规律题、函数类规律题、以几何为基础衍生出图形变换规律题、坐标变换规律题等,且每一类规律探究题均有其对应的特点。
1.数式类
该类规律题一般以数的变化为重点,常见的呈现方式有两种,一种是直接给出具有特定规律的数或算式,另一种是给出具有规律变化的代表个数的原点,均需要学生完善或进一步推演规律。
2.函数类
函数类规律题则是以初中常见的函数知识为基础,题干一般给出对应的函数关系或者关系式,需要学生结合自身对函数的理解对其加以完善,或推理出后续的函数关系式。
3.图形变换类
该类型是几何综合的代表,题干一般给出一系列具有关联性的图形,以及图形生成的具体操作,需要学生结合几何性质,从中发现衍生规律。
4.坐标变换类
该类规律题最为特殊,一般是几何与函数知识的综合,以点坐标和线段长的变换作为图形衍生递推的基础,以几何性质和数式变化作为规律生成的媒介,且在直角坐标系中构建了相应的数形规律,因此规律的探究需要调用几何与代数两大知识模块。
解题策略
规律探究题实际上就是初中数学代数与几何的排列组合,其中必然隐含着数学规律,因此解题分析过程实际上就是使用合理的策略找到问题的突破口。而对于不同类型的规律探究题,其解法策略也有所不同。
1.策略一:举例归纳,发现规律
对于一些以数值或算式为主体的规律探究题,最为快捷的方法是举例验证,即首先按顺序列举出数的运算过程和结果,然后归纳出规律,并对其加以验证。有时由于列举的数值量不够容易造成规律得出的错误,因此在列举时应适当多举例。
2.策略二:排列类比,递推规律
探究算式规律是代数类规律探究题的重要类型,题干一般会给出一系列的算式,因此在解析时可以按照一些顺序对其加以排列,通过数列推导、类比参照的方式总结其中的通式,从而获得最终答案。
3.策略三:关注特征,循序归纳
几何类规律题必然涉及几何特征或对应性质,因此在分析该类问题时需要充分把握图形的特征结构,适当结合几何性质,根据图形的变化特点来逐步发现其中的变化规律,并对其加以总结。
4.策略四:数形结合,衍生规律
而对于以直角坐标系为基础构建的图形变化规律,考虑到其中涉及几何变化和点坐标、线段长的递变,因此采用数形结合的解题策略更为有效。即首先从野形冶的角度理解图形变化,提取其中的几何特征,然后从“数”的角度,借助直角坐标系将点和线的变化数量化,并构建相应的规律模型,最终实现求解。
【学以致用】
1.的个位数是( )
A.4 B.2 C.6 D.8
2.根据如图所示的,②,③三个图所表示的规律,依次下去第n个图中平行四边形的个数是( )
A. B. C. D.
3.观察下列各单项式:,,,,,,,根据你发现的规律,第10个单项式是( )
A. B. C. D.
4.对于正数,规定,例如:,则的值为( )
A.2021 B.2020 C.2019.5 D.2020.5
5.观察下列等式:,,,,,,.根据这个规律,可知的末尾数字是( )
A.0 B.2 C.4 D.6
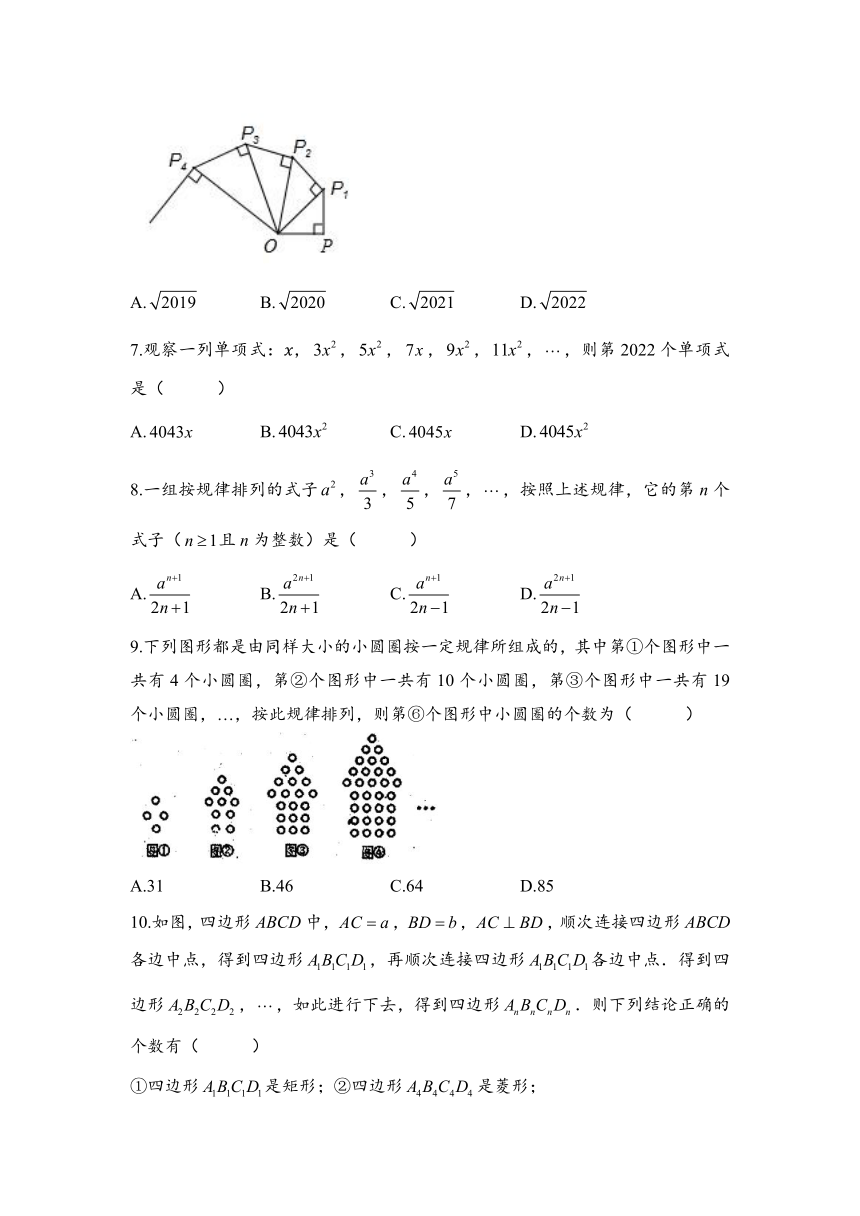
6.如图,,过点P作且,得;再过点作且,得;又过点作且,得,依此法继续作下去,得( )
A. B. C. D.
7.观察一列单项式:,,,,,,,则第2022个单项式是( )
A. B. C. D.
8.一组按规律排列的式子,,,,,按照上述规律,它的第n个式子(且n为整数)是( )
A. B. C. D.
9.下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,…,按此规律排列,则第⑥个图形中小圆圈的个数为( )
A.31 B.46 C.64 D.85
10.如图,四边形ABCD中,,,,顺次连接四边形ABCD各边中点,得到四边形,再顺次连接四边形各边中点.得到四边形,,如此进行下去,得到四边形.则下列结论正确的个数有( )
①四边形是矩形;②四边形是菱形;
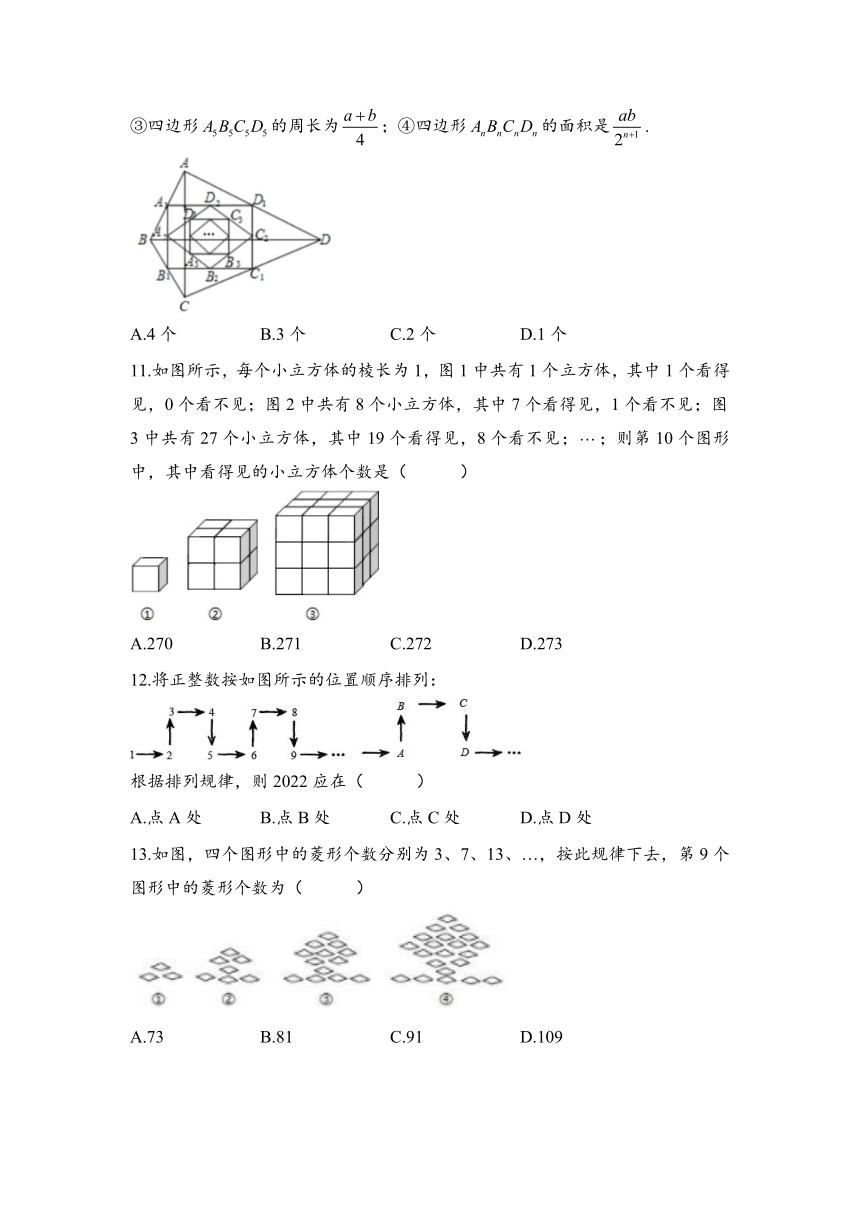
③四边形的周长为;④四边形的面积是.
A.4个 B.3个 C.2个 D.1个
11.如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;;则第10个图形中,其中看得见的小立方体个数是( )
A.270 B.271 C.272 D.273
12.将正整数按如图所示的位置顺序排列:
根据排列规律,则2022应在( )
A.点A处 B.点B处 C.点C处 D.点D处
13.如图,四个图形中的菱形个数分别为3、7、13、…,按此规律下去,第9个图形中的菱形个数为( )
A.73 B.81 C.91 D.109
14.如图4-1~图4-4,将形状、大小完全相同的“”和线段按照一定规律摆成下列图形,图4-1中“”的个数为,图4-2中“”的个数为,图4-3中“”的个数为,,以此类推,则的值为( )
A. B. C. D.
15.如图1,已知,D为的角平分线上面一点.连接BD,CD;如图2,已知,D,E为的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知,D,E,F为的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;,依次规律,第个图形中有全等三角形的对数是( )
A. B. C. D.
16.如图,点,,,在反比例函数的图象上,点,,,,在轴上,且,直线与双曲线交于点,,,,,则(为正整数)的坐标是( )
A. B. C. D.
17.如图,中,,,.点,,分别是边,,的中点;点,,分别是边,,的中点;,以此类推,则第2021个三角形的周长是( )
A. B. C. D.
18.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建的正三角形和正六边形共用了2023根火柴,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建的正三角形的个数是( )
A.229 B.281 C.287 D.293
19.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第(是大于0的整数)个图形需要黑色棋子的个数是( )
A. B. C. D.
20.如图,在平面直角坐标系上有点,点A第一次跳动至点,第二次向右跳动3个单位至点,第三次跳动至点,第四次向右跳动5个单位至点,,以此规律跳动下去,点A第2021次跳动至点的坐标是( )
A. B.
C. D.
21.如图,一个点在第一象限及x轴、轴上移动,在第一秒钟,它从原点移动到点,然后按照图中箭头所示方向移动,即
且每秒移动一个单位,那么第2021秒时,点所在位置的坐标是( )
A. B. C. D.
22.已知正方形,,按如图所示放置,点,,在直线上,,,,在轴上,则线段的长为( )
A. B. C. D.
23.如图在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B,O分别落在点,处,点在轴上,再将绕点顺时针旋转到的位置,点在轴上,将绕点顺时针旋转到的位置,点在轴上,依次进行下去.若点,,则点的坐标为( )
A. B. C. D.
24.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,,根据这个规律探索可得第2019个点的坐标是( )
A. B.
C. D.
25.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第2022次运动后,动点P的坐标是( )
A. B. C. D.(2022,2)
26.如图,一个机器人从点O出发,向正西方向走到达点,再向正北方向走到达点,再向正东方向走到达点,再向正南方向走到达点,再向正西方向走到达点,,按如此规律走下去,当机器人走到点时,点的坐标为( )
A. B.
C. D.
27.定义:若抛物线的顶点与轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线经过点,一组抛物线的顶点,,,,(n为正整数)依次是直线上的点,这组抛物线与轴正半轴的交点依次是:,,,,(为正整数).若,当d为何值时,这组抛物线中存在“美丽抛物线”对于这道题目,甲的结果是,乙的结果是,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
28.如图,一段抛物线,记为,它与轴交于点O和;将绕旋转得到,交轴于;将绕旋转得到,交轴于,如此进行下去,若点在某段抛物线上,则的值为( )
A.0 B. C.2 D.
29.观察以下等式:
第1个等式:
第2个等式:
第3个等式:
第4个等式:
第5个等式:
按照以上规律,解决下列问题:
(1)写出第6个等式:
(2)写出你猜想的第个等式:________(用含的等式表示),并证明.
30.观察下面的图案和算式,解答问题:
(1)请猜想________
(2)请猜想________
(3)请用上述规律计算:的值.
规律探究专题
【参考答案】
1.解:C
2.解:从图中我们发现
(1)中有6个平行四边形,;
(2)中有18个平行四边形,;
(3)中有36个平行四边形,;
∴第n个中有个平行四边形.
故选B
3.解:B
4.解:C
5.解:A
6.解:D
7.解:B
8.解:C
9.解:C
10.解:A
11.解:B
12.解:A
13.解:C
14.解:C
15.解:∵AD是的平分线,
∴.
在与中,
∴.
∴图1中有1对全等三角形.
同理:图2中,,
∴.
∵,
∴.
在和中,
∴,
∴图2中有对全等三角形.
同理:图3中有对全等三角形.
由此发现:第个图形中全等三角形的对数是:.
故选C.
16.解:由题意,联立,
解得,
∴,
∴,.
∵,
∴为等腰直角三角形,
∴.
如图,过作交轴于H,
则.
设,则,
∴,
解得,(舍),
∴,
∴,
∴,
同理可得,,
∴,
即.
故选D.
17.解:∵,分别是边,的中点,
∴线段是的中位线,
∴;
同理:,,
∴,
∴第2个三角形的周长是第1个三角形周长的一半,
同理:第3个三角形的周长是第2个三角形周长的一半,……
第个三角形的周长是第个三角形周长的一半;
∵,,,
∴第1个三角形的周长是,
第2个三角形的周长是;
第3个三角形的周长是;
……
第个三角形的周长是;
当时,第2021个三角形的周长是.
故选A.
18.解:设连续搭建正三角形的个数为个,连续搭建正六边形的个数为个,
由题意得:,解得
故选D.
19.解:第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋子个;
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子个;
第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子个;
按照这样的规律摆下去,
则第个图形需要黑色棋子的个数是.
故选C.
20.解:因为,,,,,,
,,,(为正整数).
令,可得,
所以.
故选D
21.解:观察可发现,点到用秒,到用秒,到用秒,则可知当点离开x轴时的横坐标为时间的平方,当点离开轴时的纵坐标为时间的平方,此时时间为奇数的点在x轴上,时间为偶数的点在轴上,
∴第2025秒时,动点在,故第2021秒时,动点在向左一个单位,再向上3个单位,即的位置.
22.解:根据条件,可以得到该直线与轴的夹角是,且,
再结合正方形条件,可以判定所有三角形都是等腰直角三角形,
∴,
,
同理,…
则的高度是,
所以当时,点到轴的距离是,即,
则.
故选B.
23.解:∵,
∴,
∴,
∴的横坐标为6,
∴的横坐标为,
∴点的横坐标为,
点的纵坐标为0,即的坐标为.
故选C.
24.解:A
25.解:B
26.解:观察图象可知,下标为偶数时在第二、四象限,下标为奇数时在第一、三象限,且被4整除在第四象限,
因为,
所以在第四象限,即坐标为.
故选B
27.解:直线经过点,
则,∴直线.
由抛物线的对称性知,抛物线的顶点与轴的两个交点构成的直角三角形必为等腰直角三角形,
∴该等腰直角三角形的高等于斜边的一半.
∵,
∴该等腰直角三角形的斜边长小于2,斜边上的高小于1(即抛物线的顶点纵坐标小于1).
∵当时,;
当时,;
当时,,
∴美丽抛物线的顶点只有、.
①若为顶点,由得;
②若为顶点,由)得,
综上所述,为或时,存在美丽抛物线.
故选B
28.解:当时,,
解得:,,
∴点的坐标为.
由旋转的性质,可知:点的坐标为.
∵,
∴当时,.
由图象可知:当时的值与当时的值互为相反数,
∴.
故选C
29.解:(1)
(2),
证明:等式左边
等式右边,即.
30.解:(1);
(2);
(3)根据题意,得原式
初中数学的知识内容大致可以分为代数和几何两类,这个分类对于规律探究题同样适用,中考在考查时只是做了进一步的细化,例如以数为基础进一步衍生出数式类规律题、函数类规律题、以几何为基础衍生出图形变换规律题、坐标变换规律题等,且每一类规律探究题均有其对应的特点。
1.数式类
该类规律题一般以数的变化为重点,常见的呈现方式有两种,一种是直接给出具有特定规律的数或算式,另一种是给出具有规律变化的代表个数的原点,均需要学生完善或进一步推演规律。
2.函数类
函数类规律题则是以初中常见的函数知识为基础,题干一般给出对应的函数关系或者关系式,需要学生结合自身对函数的理解对其加以完善,或推理出后续的函数关系式。
3.图形变换类
该类型是几何综合的代表,题干一般给出一系列具有关联性的图形,以及图形生成的具体操作,需要学生结合几何性质,从中发现衍生规律。
4.坐标变换类
该类规律题最为特殊,一般是几何与函数知识的综合,以点坐标和线段长的变换作为图形衍生递推的基础,以几何性质和数式变化作为规律生成的媒介,且在直角坐标系中构建了相应的数形规律,因此规律的探究需要调用几何与代数两大知识模块。
解题策略
规律探究题实际上就是初中数学代数与几何的排列组合,其中必然隐含着数学规律,因此解题分析过程实际上就是使用合理的策略找到问题的突破口。而对于不同类型的规律探究题,其解法策略也有所不同。
1.策略一:举例归纳,发现规律
对于一些以数值或算式为主体的规律探究题,最为快捷的方法是举例验证,即首先按顺序列举出数的运算过程和结果,然后归纳出规律,并对其加以验证。有时由于列举的数值量不够容易造成规律得出的错误,因此在列举时应适当多举例。
2.策略二:排列类比,递推规律
探究算式规律是代数类规律探究题的重要类型,题干一般会给出一系列的算式,因此在解析时可以按照一些顺序对其加以排列,通过数列推导、类比参照的方式总结其中的通式,从而获得最终答案。
3.策略三:关注特征,循序归纳
几何类规律题必然涉及几何特征或对应性质,因此在分析该类问题时需要充分把握图形的特征结构,适当结合几何性质,根据图形的变化特点来逐步发现其中的变化规律,并对其加以总结。
4.策略四:数形结合,衍生规律
而对于以直角坐标系为基础构建的图形变化规律,考虑到其中涉及几何变化和点坐标、线段长的递变,因此采用数形结合的解题策略更为有效。即首先从野形冶的角度理解图形变化,提取其中的几何特征,然后从“数”的角度,借助直角坐标系将点和线的变化数量化,并构建相应的规律模型,最终实现求解。
【学以致用】
1.的个位数是( )
A.4 B.2 C.6 D.8
2.根据如图所示的,②,③三个图所表示的规律,依次下去第n个图中平行四边形的个数是( )
A. B. C. D.
3.观察下列各单项式:,,,,,,,根据你发现的规律,第10个单项式是( )
A. B. C. D.
4.对于正数,规定,例如:,则的值为( )
A.2021 B.2020 C.2019.5 D.2020.5
5.观察下列等式:,,,,,,.根据这个规律,可知的末尾数字是( )
A.0 B.2 C.4 D.6
6.如图,,过点P作且,得;再过点作且,得;又过点作且,得,依此法继续作下去,得( )
A. B. C. D.
7.观察一列单项式:,,,,,,,则第2022个单项式是( )
A. B. C. D.
8.一组按规律排列的式子,,,,,按照上述规律,它的第n个式子(且n为整数)是( )
A. B. C. D.
9.下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,…,按此规律排列,则第⑥个图形中小圆圈的个数为( )
A.31 B.46 C.64 D.85
10.如图,四边形ABCD中,,,,顺次连接四边形ABCD各边中点,得到四边形,再顺次连接四边形各边中点.得到四边形,,如此进行下去,得到四边形.则下列结论正确的个数有( )
①四边形是矩形;②四边形是菱形;
③四边形的周长为;④四边形的面积是.
A.4个 B.3个 C.2个 D.1个
11.如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;;则第10个图形中,其中看得见的小立方体个数是( )
A.270 B.271 C.272 D.273
12.将正整数按如图所示的位置顺序排列:
根据排列规律,则2022应在( )
A.点A处 B.点B处 C.点C处 D.点D处
13.如图,四个图形中的菱形个数分别为3、7、13、…,按此规律下去,第9个图形中的菱形个数为( )
A.73 B.81 C.91 D.109
14.如图4-1~图4-4,将形状、大小完全相同的“”和线段按照一定规律摆成下列图形,图4-1中“”的个数为,图4-2中“”的个数为,图4-3中“”的个数为,,以此类推,则的值为( )
A. B. C. D.
15.如图1,已知,D为的角平分线上面一点.连接BD,CD;如图2,已知,D,E为的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知,D,E,F为的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;,依次规律,第个图形中有全等三角形的对数是( )
A. B. C. D.
16.如图,点,,,在反比例函数的图象上,点,,,,在轴上,且,直线与双曲线交于点,,,,,则(为正整数)的坐标是( )
A. B. C. D.
17.如图,中,,,.点,,分别是边,,的中点;点,,分别是边,,的中点;,以此类推,则第2021个三角形的周长是( )
A. B. C. D.
18.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建的正三角形和正六边形共用了2023根火柴,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建的正三角形的个数是( )
A.229 B.281 C.287 D.293
19.如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第(是大于0的整数)个图形需要黑色棋子的个数是( )
A. B. C. D.
20.如图,在平面直角坐标系上有点,点A第一次跳动至点,第二次向右跳动3个单位至点,第三次跳动至点,第四次向右跳动5个单位至点,,以此规律跳动下去,点A第2021次跳动至点的坐标是( )
A. B.
C. D.
21.如图,一个点在第一象限及x轴、轴上移动,在第一秒钟,它从原点移动到点,然后按照图中箭头所示方向移动,即
且每秒移动一个单位,那么第2021秒时,点所在位置的坐标是( )
A. B. C. D.
22.已知正方形,,按如图所示放置,点,,在直线上,,,,在轴上,则线段的长为( )
A. B. C. D.
23.如图在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B,O分别落在点,处,点在轴上,再将绕点顺时针旋转到的位置,点在轴上,将绕点顺时针旋转到的位置,点在轴上,依次进行下去.若点,,则点的坐标为( )
A. B. C. D.
24.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,,根据这个规律探索可得第2019个点的坐标是( )
A. B.
C. D.
25.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第2022次运动后,动点P的坐标是( )
A. B. C. D.(2022,2)
26.如图,一个机器人从点O出发,向正西方向走到达点,再向正北方向走到达点,再向正东方向走到达点,再向正南方向走到达点,再向正西方向走到达点,,按如此规律走下去,当机器人走到点时,点的坐标为( )
A. B.
C. D.
27.定义:若抛物线的顶点与轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线经过点,一组抛物线的顶点,,,,(n为正整数)依次是直线上的点,这组抛物线与轴正半轴的交点依次是:,,,,(为正整数).若,当d为何值时,这组抛物线中存在“美丽抛物线”对于这道题目,甲的结果是,乙的结果是,则( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
28.如图,一段抛物线,记为,它与轴交于点O和;将绕旋转得到,交轴于;将绕旋转得到,交轴于,如此进行下去,若点在某段抛物线上,则的值为( )
A.0 B. C.2 D.
29.观察以下等式:
第1个等式:
第2个等式:
第3个等式:
第4个等式:
第5个等式:
按照以上规律,解决下列问题:
(1)写出第6个等式:
(2)写出你猜想的第个等式:________(用含的等式表示),并证明.
30.观察下面的图案和算式,解答问题:
(1)请猜想________
(2)请猜想________
(3)请用上述规律计算:的值.
规律探究专题
【参考答案】
1.解:C
2.解:从图中我们发现
(1)中有6个平行四边形,;
(2)中有18个平行四边形,;
(3)中有36个平行四边形,;
∴第n个中有个平行四边形.
故选B
3.解:B
4.解:C
5.解:A
6.解:D
7.解:B
8.解:C
9.解:C
10.解:A
11.解:B
12.解:A
13.解:C
14.解:C
15.解:∵AD是的平分线,
∴.
在与中,
∴.
∴图1中有1对全等三角形.
同理:图2中,,
∴.
∵,
∴.
在和中,
∴,
∴图2中有对全等三角形.
同理:图3中有对全等三角形.
由此发现:第个图形中全等三角形的对数是:.
故选C.
16.解:由题意,联立,
解得,
∴,
∴,.
∵,
∴为等腰直角三角形,
∴.
如图,过作交轴于H,
则.
设,则,
∴,
解得,(舍),
∴,
∴,
∴,
同理可得,,
∴,
即.
故选D.
17.解:∵,分别是边,的中点,
∴线段是的中位线,
∴;
同理:,,
∴,
∴第2个三角形的周长是第1个三角形周长的一半,
同理:第3个三角形的周长是第2个三角形周长的一半,……
第个三角形的周长是第个三角形周长的一半;
∵,,,
∴第1个三角形的周长是,
第2个三角形的周长是;
第3个三角形的周长是;
……
第个三角形的周长是;
当时,第2021个三角形的周长是.
故选A.
18.解:设连续搭建正三角形的个数为个,连续搭建正六边形的个数为个,
由题意得:,解得
故选D.
19.解:第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋子个;
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子个;
第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子个;
按照这样的规律摆下去,
则第个图形需要黑色棋子的个数是.
故选C.
20.解:因为,,,,,,
,,,(为正整数).
令,可得,
所以.
故选D
21.解:观察可发现,点到用秒,到用秒,到用秒,则可知当点离开x轴时的横坐标为时间的平方,当点离开轴时的纵坐标为时间的平方,此时时间为奇数的点在x轴上,时间为偶数的点在轴上,
∴第2025秒时,动点在,故第2021秒时,动点在向左一个单位,再向上3个单位,即的位置.
22.解:根据条件,可以得到该直线与轴的夹角是,且,
再结合正方形条件,可以判定所有三角形都是等腰直角三角形,
∴,
,
同理,…
则的高度是,
所以当时,点到轴的距离是,即,
则.
故选B.
23.解:∵,
∴,
∴,
∴的横坐标为6,
∴的横坐标为,
∴点的横坐标为,
点的纵坐标为0,即的坐标为.
故选C.
24.解:A
25.解:B
26.解:观察图象可知,下标为偶数时在第二、四象限,下标为奇数时在第一、三象限,且被4整除在第四象限,
因为,
所以在第四象限,即坐标为.
故选B
27.解:直线经过点,
则,∴直线.
由抛物线的对称性知,抛物线的顶点与轴的两个交点构成的直角三角形必为等腰直角三角形,
∴该等腰直角三角形的高等于斜边的一半.
∵,
∴该等腰直角三角形的斜边长小于2,斜边上的高小于1(即抛物线的顶点纵坐标小于1).
∵当时,;
当时,;
当时,,
∴美丽抛物线的顶点只有、.
①若为顶点,由得;
②若为顶点,由)得,
综上所述,为或时,存在美丽抛物线.
故选B
28.解:当时,,
解得:,,
∴点的坐标为.
由旋转的性质,可知:点的坐标为.
∵,
∴当时,.
由图象可知:当时的值与当时的值互为相反数,
∴.
故选C
29.解:(1)
(2),
证明:等式左边
等式右边,即.
30.解:(1);
(2);
(3)根据题意,得原式
同课章节目录
