8.5乘法公式复习教学案

乘法公式（二）(教学案)
班级 姓名
完全平方公式
学习目标
1、完全平方公式的推导及其应用．
2、完全平方公式的几何解释．
3、经历探索完全平方公式的过程，进一步发展符号感和推理能力．
4、重视学生对算理的理解，有意识地培养学生的思维条理性和表达能力．
学习重点
完全平方公式的推导过程、结构特点、几何解释，灵活应用．学习难点理解完全平方公式的结构特征并能灵活应用公式进行计算．
一、提出问题，创设情境
一位老人非常喜欢孩子．每当有孩子到他家做 ( http: / / www.21cnjy.com )客时，老人都要拿出糖果招待他们．来一个孩子，老人就给这个孩子一块糖，来两个孩子，老人就给每个孩子两块塘，…
(1)第一天有个男孩去了老人家，老人一共给了这些孩子多少块糖？
(2)第二天有个女孩去了老人家，老人一共给了这些孩子多少块糖？
(3)第三天有个孩子一起去看老人，老人一共给了这些孩子多少块糖？
(4)这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多？
(这个问题如何计算？列出算式即可)
(5)在这里出现了两个数的和的平方，这节课，我们主要研究这一内容。二、深入研究，合作创新
1.问题：根据乘方的定义，我们知道：，那么应该写成什么样的形式呢？的运算结果有什么规律？尝试计算下列各式，看看能不能发现什么规律？
(1) ；
(2) ；
(3) ；
(4) ；
2.观察所得结果，你能发现什么规律吗？
3.学生归纳，教师板演，得到完全平方公式
即：两数和（或差）的平方，等于它们的平方和，加（或减）它们的积的2倍．
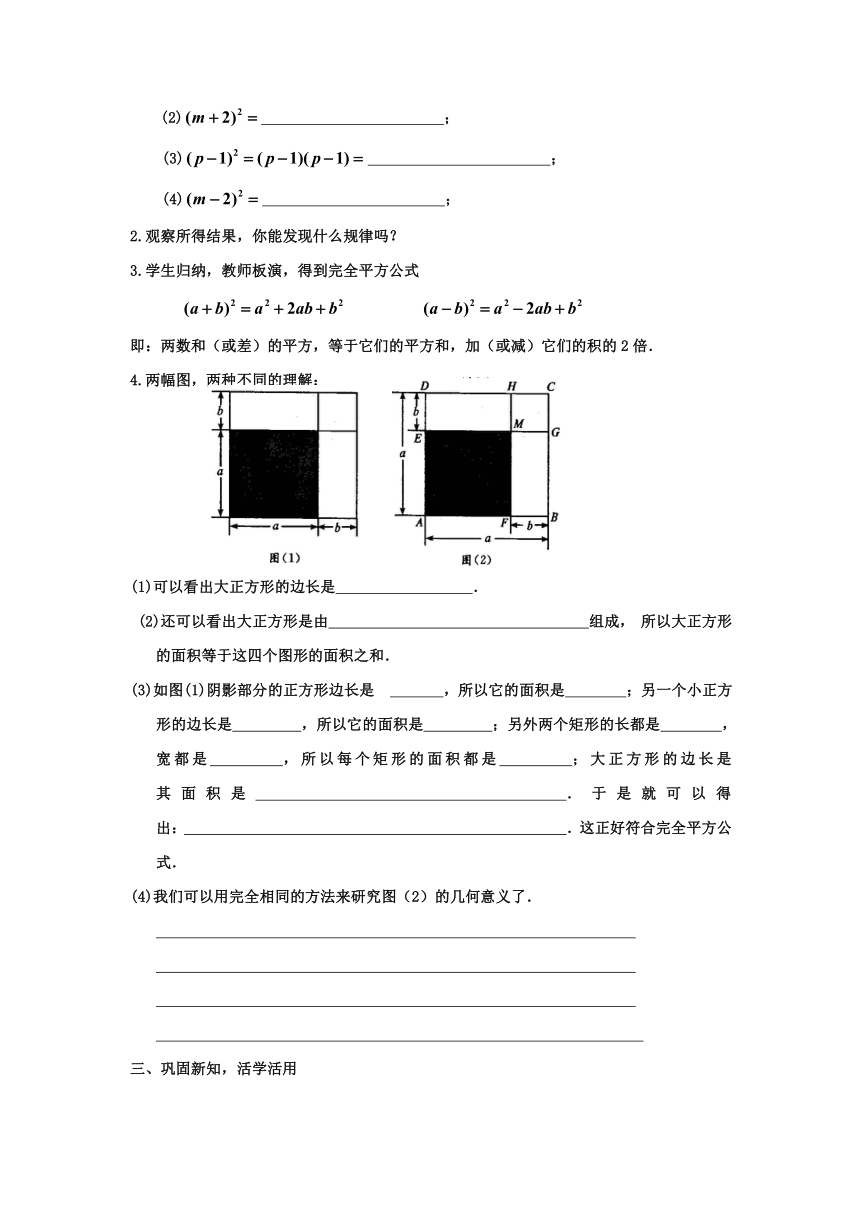
4.两幅图，两种不同的理解：
(1)可以看出大正方形的边长是 ．
(2)还可以看出大正方形是由 组成，所以大正方形的面积等于这四个图形的面积之和．
(3)如图(1)阴影部分的正方形边长是 ( http: / / www.21cnjy.com ) ，所以它的面积是 ；另一个小正方形的边长是 ，所以它的面积是 ；另外两个矩形的长都是 ，宽都是 ，所以每个矩形的面积都是 ；大正方形的边长是 其面积是 ．于是就可以得出： ．这正好符合完全平方公式．
(4)我们可以用完全相同的方法来研究图（2）的几何意义了．
三、巩固新知，活学活用
1、直接运用
（1） （2）
（3） （4）
2、运用完全平方公式计算
（1） （2）
3、计算：
(1)
(2)
(3)
(4)
4、下列多项式中，哪些是由完全平方公式得来的？
课后反思
乘法公式（一）(教学案)
班级 姓名
学习目标
1、经历探索平方差公式的过程．
2、会推导平方差公式，并能运用公式进行简单的运算．
3、在探索平方差公式的过程中，培养符号感和推理能力．
4、培养学生观察、归纳、概括的能力．
学习重点
平方差公式的推导和应用．
学习难点
理解平方差公式的结构特征，灵活应用平方差公式．
一、提出问题，创设情境
你能用简便方法计算下列各题吗？
（1） （2）
计算下列多项式的积．
（1）
（2）
（3）
（4）
观察上述算式，你发现结构上有什么的特点和规律？
运算出结果后，你发现结果又有什么特点规律？
小组内交流：再举出两个例子说明上述发现。
二、深入研究，合作创新
一般情况下，我们总有：
文字表达：
。
总的说来，能够应用上述规律去计算的式子必须满足这样一些条件：
1、要计算的式子总是 个多项式的乘积的形式；
2、每个多项式总可以理解成 个部分。并且
；
当要计算的式子满足上述两个条件的时候，我们可以直接应用公式。
其中表示任意数，也可以表示任意的单项式、多项式。
注意：只有满足条件的乘法才能用公式来进行简化运算。
三、巩固新知，活学活用
例1：下列哪些式子可以运用平方差公式计算？哪些不能？为什么？
1、 2、
3、 4、
5、
例2：计算：
1、 2、
3、 4、
四、课堂检测
1、
2、
3、
4、
5、
6、
7、
8、
五、兴趣探索，深入研究
1、证明：两个连续奇数的积加上一定是一个偶数的平方
2、求证：一定是的倍数
课后反思