数学人教A版(2019)选择性必修第二册4.3.2等比数列的前n项和公式 课件(共38张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.3.2等比数列的前n项和公式 课件(共38张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 21:12:16 | ||
图片预览










文档简介
(共39张PPT)
4.3.2 等比数列的前n项和公式
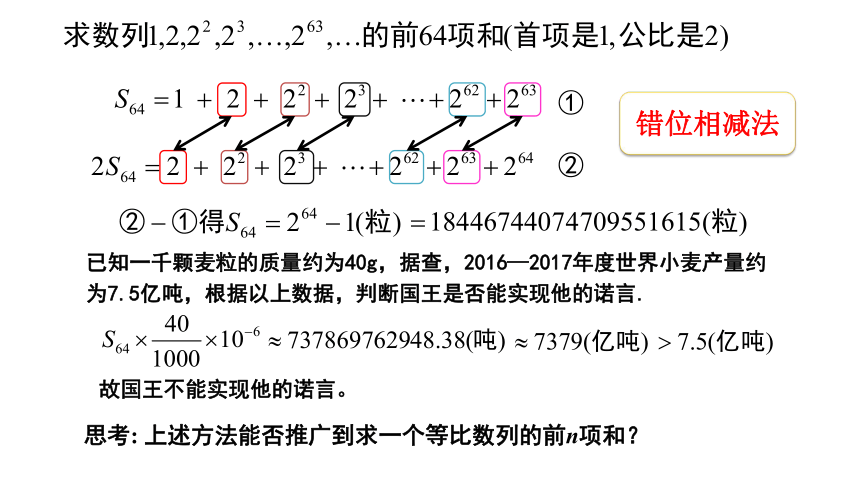
国际象棋起源于古代印度. 相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里放的麦粒都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”
国王觉得这个要求不高,就欣然同意了. 已知1000颗麦粒的质量约为40 g,据查,2016—2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.
问题 把上述问题中每个格子里放的麦粒数看成一个数列,请分析这个数列是否是等比数列 若是,请求出通项公式,并思考国王能满足象棋发明者的要求吗?
“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒……依此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子。请给我足够的粮食来实现上述要求”。
各个格子里的麦粒数依次是:
发明者要求的麦粒总数:
等比数列
等比数列
前64项和
错位相减法
已知一千颗麦粒的质量约为40g,据查,2016—2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.
故国王不能实现他的诺言。
思考: 上述方法能否推广到求一个等比数列的前n项和?
错位相减法
等比数列的前n项和公式:
按1000颗麦粒的质量为40g,那么象棋发明者想要的麦粒总质量超过7000亿吨,约是2016-2017年度世界小麦产量的981倍,因此,国王根本不可能实现他的诺言.
例7 已知数列{an}是等比数列.
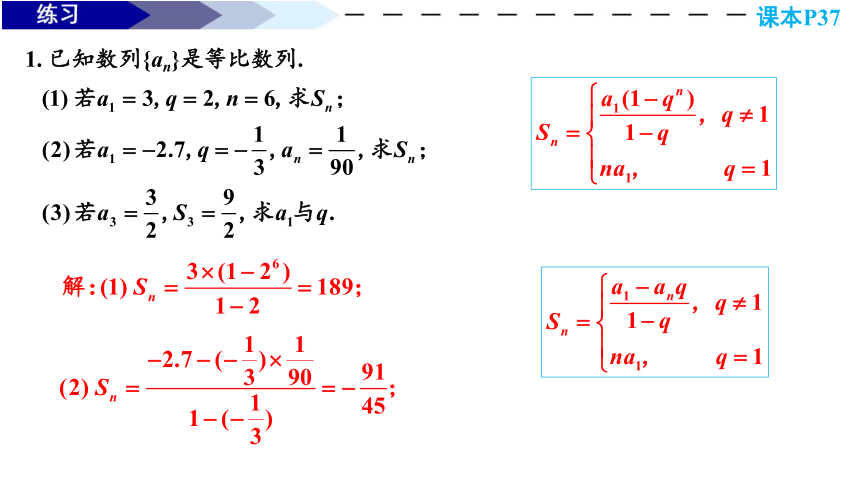
1. 已知数列{an}是等比数列.
课本P37
1. 已知数列{an}是等比数列.
课本P37
▲若q未知,用等比数列前n项和公式时要考虑q是否为1.
若q未知,用公式时要考虑q是否为1
法1:
法2:
练习4.在等比数列{an}中,已知a1+a2+…+an=2n-1,则a12+a22+…+an2等于________.
新知2:等比数列的前n项和的性质
qn的系数和常数项互为相反数
﹣1
﹣2
想一想,不用分类讨论的方式能否证明该结论?
新知2:等比数列的前n项和的性质
新知2:等比数列的前n项和的性质
练习6.
练习7.
例10 如图,正方形ABCD的边长为5cm,取正方形ABCD各边的中点E, F, G, H,作第2个正方形EFGH,然后再取正方形EFGH各边的中点I, J, K, L,作第3个正方形IJKL,依此方法一直继续下去.
(1) 求从正方形ABCD开始,连续10个正方形的面积之和;
(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少
例10 如图,正方形ABCD的边长为5cm,取正方形ABCD各边的中点E, F, G, H,作第2个正方形EFGH,然后再取正方形EFGH各边的中点I, J, K, L,作第3个正方形IJKL,依此方法一直继续下去.
(1) 求从正方形ABCD开始,连续10个正方形的面积之和;
(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少
课本P38/39-例11.去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理。预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨。为了确定处理生活垃圾的预算,请你测算一下从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
分析:每年生活垃圾的总量构成等比数列,公比为1+5%;
每年以环保方式处理的垃圾量构成等差数列,公差为1.5;
从今年起5年内通过填埋方式处理的垃圾总量约为63.5万吨。
例12 某牧场今年初牛的存栏数为1200,预计以后每年存栏数的增长率为8%,且在每年年底卖出100头牛,设牧场从今年起每年年初的计划存栏数依次为c1,c2,c3, .
(1)写出一个递推公式,表示cn+1与cn之间的关系;
(2) 将(1)中的递推公式表示成cn+1-k = r(cn-k)的形式,其中k,r为常数;
(3) 求S10= c1+c2+c3+ +c10的值(精确到1).
例12 某牧场今年初牛的存栏数为1200,预计以后每年存栏数的增长率为8%,且在每年年底卖出100头牛,设牧场从今年起每年年初的计划存栏数依次为c1,c2,c3, .
(1)写出一个递推公式,表示cn+1与cn之间的关系;
(2) 将(1)中的递推公式表示成cn+1-k = r(cn-k)的形式,其中k,r为常数;
(3) 求S10= c1+c2+c3+ +c10的值(精确到1).
方法归纳:解数列应用题
(1)认真审题,明确问题是等差数列问题?还是等比数列问题?还是含有递推公式的数列问题?是求an,还是求Sn?
①特别要注意项数是多少.
②细胞繁殖、利率、增长率等问题一般为等比数列问题.
(2)抓住数量关系,联想数学知识和数学方法,恰当引入参数变量,将文字语言翻译成数学语言,将数量关系用数学式子表达.
(3)将实际问题抽象为数学问题,将已知与所求联系起来,列出满足题意的数学关系式.
特征方程法
1. 已知a ≠ b,且ab ≠ 0,对于n∈N*,证明:
课本P37
环节六:归纳总结,反思提升
等差数列 等比数列
定义
通项公式
前n项和公式
中项
性质
依次n项和仍成等差数列,
公差为n2d
依次n项和仍成等比数列,
公比为qn
小结:
1. 等比数列的前n项和公式:
4.3.2 等比数列的前n项和公式
国际象棋起源于古代印度. 相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里放的麦粒都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”
国王觉得这个要求不高,就欣然同意了. 已知1000颗麦粒的质量约为40 g,据查,2016—2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.
问题 把上述问题中每个格子里放的麦粒数看成一个数列,请分析这个数列是否是等比数列 若是,请求出通项公式,并思考国王能满足象棋发明者的要求吗?
“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒……依此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子。请给我足够的粮食来实现上述要求”。
各个格子里的麦粒数依次是:
发明者要求的麦粒总数:
等比数列
等比数列
前64项和
错位相减法
已知一千颗麦粒的质量约为40g,据查,2016—2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.
故国王不能实现他的诺言。
思考: 上述方法能否推广到求一个等比数列的前n项和?
错位相减法
等比数列的前n项和公式:
按1000颗麦粒的质量为40g,那么象棋发明者想要的麦粒总质量超过7000亿吨,约是2016-2017年度世界小麦产量的981倍,因此,国王根本不可能实现他的诺言.
例7 已知数列{an}是等比数列.
1. 已知数列{an}是等比数列.
课本P37
1. 已知数列{an}是等比数列.
课本P37
▲若q未知,用等比数列前n项和公式时要考虑q是否为1.
若q未知,用公式时要考虑q是否为1
法1:
法2:
练习4.在等比数列{an}中,已知a1+a2+…+an=2n-1,则a12+a22+…+an2等于________.
新知2:等比数列的前n项和的性质
qn的系数和常数项互为相反数
﹣1
﹣2
想一想,不用分类讨论的方式能否证明该结论?
新知2:等比数列的前n项和的性质
新知2:等比数列的前n项和的性质
练习6.
练习7.
例10 如图,正方形ABCD的边长为5cm,取正方形ABCD各边的中点E, F, G, H,作第2个正方形EFGH,然后再取正方形EFGH各边的中点I, J, K, L,作第3个正方形IJKL,依此方法一直继续下去.
(1) 求从正方形ABCD开始,连续10个正方形的面积之和;
(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少
例10 如图,正方形ABCD的边长为5cm,取正方形ABCD各边的中点E, F, G, H,作第2个正方形EFGH,然后再取正方形EFGH各边的中点I, J, K, L,作第3个正方形IJKL,依此方法一直继续下去.
(1) 求从正方形ABCD开始,连续10个正方形的面积之和;
(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少
课本P38/39-例11.去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理。预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨。为了确定处理生活垃圾的预算,请你测算一下从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
分析:每年生活垃圾的总量构成等比数列,公比为1+5%;
每年以环保方式处理的垃圾量构成等差数列,公差为1.5;
从今年起5年内通过填埋方式处理的垃圾总量约为63.5万吨。
例12 某牧场今年初牛的存栏数为1200,预计以后每年存栏数的增长率为8%,且在每年年底卖出100头牛,设牧场从今年起每年年初的计划存栏数依次为c1,c2,c3, .
(1)写出一个递推公式,表示cn+1与cn之间的关系;
(2) 将(1)中的递推公式表示成cn+1-k = r(cn-k)的形式,其中k,r为常数;
(3) 求S10= c1+c2+c3+ +c10的值(精确到1).
例12 某牧场今年初牛的存栏数为1200,预计以后每年存栏数的增长率为8%,且在每年年底卖出100头牛,设牧场从今年起每年年初的计划存栏数依次为c1,c2,c3, .
(1)写出一个递推公式,表示cn+1与cn之间的关系;
(2) 将(1)中的递推公式表示成cn+1-k = r(cn-k)的形式,其中k,r为常数;
(3) 求S10= c1+c2+c3+ +c10的值(精确到1).
方法归纳:解数列应用题
(1)认真审题,明确问题是等差数列问题?还是等比数列问题?还是含有递推公式的数列问题?是求an,还是求Sn?
①特别要注意项数是多少.
②细胞繁殖、利率、增长率等问题一般为等比数列问题.
(2)抓住数量关系,联想数学知识和数学方法,恰当引入参数变量,将文字语言翻译成数学语言,将数量关系用数学式子表达.
(3)将实际问题抽象为数学问题,将已知与所求联系起来,列出满足题意的数学关系式.
特征方程法
1. 已知a ≠ b,且ab ≠ 0,对于n∈N*,证明:
课本P37
环节六:归纳总结,反思提升
等差数列 等比数列
定义
通项公式
前n项和公式
中项
性质
依次n项和仍成等差数列,
公差为n2d
依次n项和仍成等比数列,
公比为qn
小结:
1. 等比数列的前n项和公式:
