2015年春七下数学专题复习 第9章 多边形 课件
文档属性
| 名称 | 2015年春七下数学专题复习 第9章 多边形 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 588.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-04 17:18:27 | ||
图片预览










文档简介
课件35张PPT。阶段专题复习
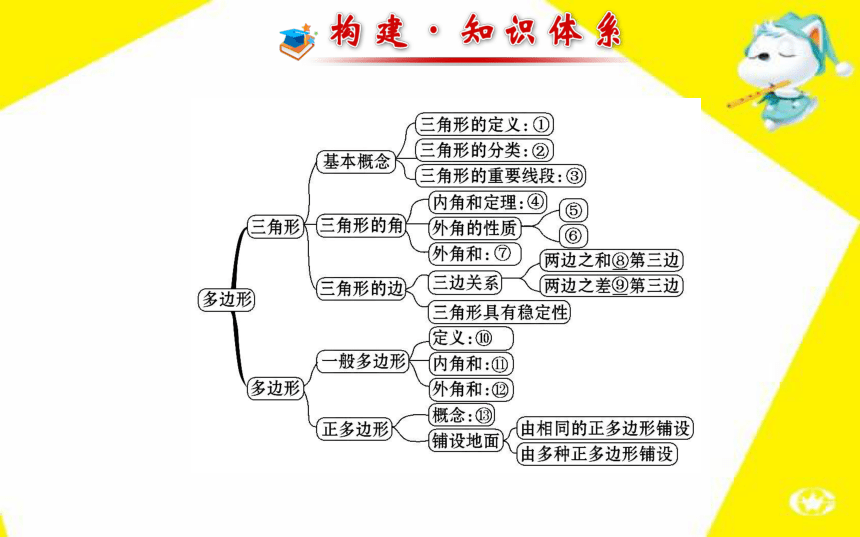
第 9 章请写出框图中数字处的内容:
①___________________________________________________
_____;
②___________________________________________________
_______________________________;
③___________________________________________;
④________________________;
⑤_____________________________________________;由三条不在同一条直线上的线段首尾顺次连结组成的平面图形按角分类:锐角三角形、直角三角形、钝角三角形;按边分类:不等边三角形、等腰三角形三角形的高、三角形的中线、三角形的角平分线三角形的内角和等于180°三角形的一个外角等于与它不相邻的两个内角的和⑥_____________________________________________;
⑦________________________; ⑧_____; ⑨_____;
⑩____________________________________________________;
?_____________; ?______;
?_________________________________.三角形的一个外角大于任何一个与它不相邻的内角三角形的外角和等于360°大于小于由n条不在同一直线上的线段首尾顺次连结组成的平面图形(n-2)·180°360°各边都相等、各角也都相等的多边形考点 1 三角形的三边关系?
【知识点睛】
1.三角形的三边关系:
(1)任意两边之和大于第三边.
(2)任意两边之差小于第三边.
2.判断三条线段能否围成三角形的方法:
(1)将两条较短线段之和与最长的线段比较.
(2)将最长边与最短边之差与第三条线段比较.【例1】(2012·海南中考)一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
A.3cm B.4cm C.7cm D.11cm
【思路点拨】三边关系→确定第三边取值范围→答案
【自主解答】选C.设第三边长为xcm,则由三角形三边关系得7-31.(2013·温州中考)下列各组数可能是一个三角形的边长的
是( )
A.1,2,4 B.4,5,9 C.4,6,8 D.5,5,11
【解析】选C.∵1+2<4,4+5=9,5+5<11,∴选项A,B,D不可能是一个三角形的边长,而4+6>8,8-6<4,∴选项C是一个三角形的边长.2.(2013·广安中考)等腰三角形的一边长为6,另一边长为13,则它的周长为( )
A.25 B.25或32 C.32 D.19
【解析】选C.当长为6的边为腰时,6+6<13不能组成三角形;所以长为6的边为底,周长为13×2+6=32.3.(2013·徐州模拟)已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A.2 B.3 C.5 D.13
【解析】选B.由题意可得,
解得,11所以,x为12,13,14.故这样的三角形个数为3.【归纳整合】三角形三边关系的应用题型
三角形的三条边之间主要有这样的关系:三角形的两边的和大于第三边,三角形的两边的差小于第三边.利用这两个关系可以解决许多典型的几何题目:
(1)确定三角形某一边的取值范围问题.
(2)判定三条线段能否组成三角形问题.
(3)求三角形某一边的长度问题.
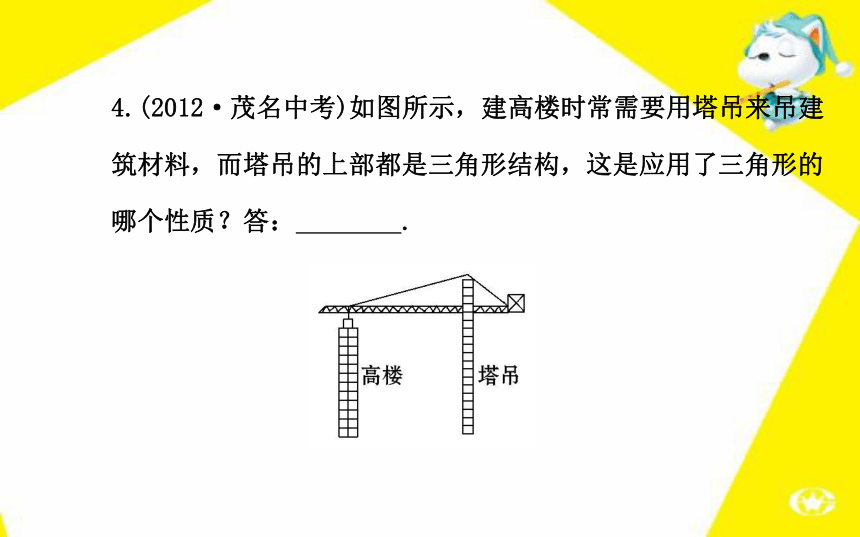
(4)求三角形的周长问题.4.(2012·茂名中考)如图所示,建高楼时常需要用塔吊来吊建筑材料,而塔吊的上部都是三角形结构,这是应用了三角形的哪个性质?答: .【解析】∵塔吊的上部是三角形结构,
∴这是运用了三角形的稳定性.
答案:稳定性考点 2 与三角形有关的角?
【知识点睛】
1.三角形的内角和:三角形的三个内角的和是180°.
2.三角形的外角的性质:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任何一个与它不相邻的内角.
3.三角形的外角和:三角形的外角和是360°.
4.三角形按角分类可分为锐角三角形、直角三角形和钝角三角形.【例2】(2013·东营中考)如图,已知AB∥CD,AD和BC相交于点O,∠A=50°,∠AOB=105°,则∠C等于( )
A.20° B.25° C.35° D.45°【思路点拨】根据三角形内角和定理求出∠B,再利用平行线性质定理求出∠C.
【自主解答】选B.在△AOB中,∠B=180°-∠A-∠AOB=180°-50°-105°=25°.
又∵AB∥CD,∴∠C=∠B=25°.【中考集训】
1.(2012·漳州中考)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.45° B.60° C.75° D.90°【解析】选C.由题意和图示,可以看出角α所在的三角形的其他两个内角分别是60°和45°,
所以∠α=180°-(60°+45°)=75°.2.(2013·内江中考)把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.125° B.120° C.140° D.130° 【解析】选D.如图,由“直角三角形两锐角互余”可知,∠3=90°-∠1=90°-40°=50°.因为直尺的对边互相平行,所以∠4=∠3=50°,所以∠2=180°-∠4=130°.3.(2013·丽水中考)如图,AB∥CD,AD和BC
相交于点O,∠A=20°,∠COD=100°,则∠C
的度数是( )
A.80° B.70° C.60° D.50°
【解析】选C.因为AB∥CD,所以∠A=∠D=20°(两直线平线,内错角相等),且∠COD=100°,所以∠C=60°.4.(2012·梅州中考)如图,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( )
A.150° B.210° C.105° D.75°【解析】选A.∵△A′DE是△ABC翻折变换而成,
∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=75°,
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-75°=105°,
∴∠1+∠2=360°-2×105°=150°.5.(2013·荆州中考)如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
A.30° B.20° C.10° D.40°【解析】选C.∵AB∥CD,∠ABE=60°,
∴∠CFB=60°,又∵∠D=50°,
∴∠E=∠CFB-∠D=60°-50°=10°.6.(2013·遂宁中考)如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 .【解析】60°角的直角三角板的另一个锐角为30°,因为∠1=18°,所以∠3=12°,再根据矩形对边平行,内错角相等可得∠2=∠3=12°.
答案:12°7.(2013·武汉模拟)已知:如图,∠B=∠C,∠1=∠2,∠BAD=40°,求∠EDC的度数.【解析】△ABD中,由三角形的外角性质知:
∠ADC=∠B+∠BAD,
即∠EDC+∠1=∠B+40° ①.
同理,得:∠2=∠EDC+∠C,
∵∠1=∠2,∠B=∠C,
∴∠1=∠EDC+∠B ②,
②代入①得:
2∠EDC+∠B=∠B+40°,
即∠EDC=20°.考点 3 多边形的内角和与外角和?
【知识点睛】
1.n边形的内角和为(n-2)·180°,外角和为360°.
2.边数每增加1,内角和就增加180°,而外角和不随边数的变化而变化,都是360°.【例3】(2012·无锡中考)若一个多边形的内角和为1080°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
【思路点拨】设元→内角和公式→方程→求解
【自主解答】选C.设这个多边形的边数为n,则
180(n-2)=1080,解得:n=8.故选C.【中考集训】
1.(2013·梅州中考)一个多边形的内角和小于它的外角和,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
【解析】选A.三角形的内角和为180°,外角和等于360°,其内角和小于外角和,四边形的内角和等于外角和,五边形、六边形的内角和大于外角和,故选A.2.(2013·资阳中考)一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
【解析】选C.360°÷36°=10.3.(2013·咸宁中考)如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( )
A.30° B.36° C.38° D.45°【解析】选B.∵正五边形的内角和为(5-2)×180°=540°,
∴正五边形的内角为540°÷5=108°,
∴∠BAE=108°.
∵AB=AE,
∴∠ABE=∠AEB=36°.
∵l∥BE,
∴∠1=∠AEB=36°.4.(2013·巴中中考)若一个多边形的内角和与外角和相等,则这个多边形是 边形.
【解析】设这个多边形的边数为n,可得(n-2)×180° =360°,解得n=4,故是四边形.
答案:四
第 9 章请写出框图中数字处的内容:
①___________________________________________________
_____;
②___________________________________________________
_______________________________;
③___________________________________________;
④________________________;
⑤_____________________________________________;由三条不在同一条直线上的线段首尾顺次连结组成的平面图形按角分类:锐角三角形、直角三角形、钝角三角形;按边分类:不等边三角形、等腰三角形三角形的高、三角形的中线、三角形的角平分线三角形的内角和等于180°三角形的一个外角等于与它不相邻的两个内角的和⑥_____________________________________________;
⑦________________________; ⑧_____; ⑨_____;
⑩____________________________________________________;
?_____________; ?______;
?_________________________________.三角形的一个外角大于任何一个与它不相邻的内角三角形的外角和等于360°大于小于由n条不在同一直线上的线段首尾顺次连结组成的平面图形(n-2)·180°360°各边都相等、各角也都相等的多边形考点 1 三角形的三边关系?
【知识点睛】
1.三角形的三边关系:
(1)任意两边之和大于第三边.
(2)任意两边之差小于第三边.
2.判断三条线段能否围成三角形的方法:
(1)将两条较短线段之和与最长的线段比较.
(2)将最长边与最短边之差与第三条线段比较.【例1】(2012·海南中考)一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
A.3cm B.4cm C.7cm D.11cm
【思路点拨】三边关系→确定第三边取值范围→答案
【自主解答】选C.设第三边长为xcm,则由三角形三边关系得7-3
是( )
A.1,2,4 B.4,5,9 C.4,6,8 D.5,5,11
【解析】选C.∵1+2<4,4+5=9,5+5<11,∴选项A,B,D不可能是一个三角形的边长,而4+6>8,8-6<4,∴选项C是一个三角形的边长.2.(2013·广安中考)等腰三角形的一边长为6,另一边长为13,则它的周长为( )
A.25 B.25或32 C.32 D.19
【解析】选C.当长为6的边为腰时,6+6<13不能组成三角形;所以长为6的边为底,周长为13×2+6=32.3.(2013·徐州模拟)已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A.2 B.3 C.5 D.13
【解析】选B.由题意可得,
解得,11
三角形的三条边之间主要有这样的关系:三角形的两边的和大于第三边,三角形的两边的差小于第三边.利用这两个关系可以解决许多典型的几何题目:
(1)确定三角形某一边的取值范围问题.
(2)判定三条线段能否组成三角形问题.
(3)求三角形某一边的长度问题.
(4)求三角形的周长问题.4.(2012·茂名中考)如图所示,建高楼时常需要用塔吊来吊建筑材料,而塔吊的上部都是三角形结构,这是应用了三角形的哪个性质?答: .【解析】∵塔吊的上部是三角形结构,
∴这是运用了三角形的稳定性.
答案:稳定性考点 2 与三角形有关的角?
【知识点睛】
1.三角形的内角和:三角形的三个内角的和是180°.
2.三角形的外角的性质:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任何一个与它不相邻的内角.
3.三角形的外角和:三角形的外角和是360°.
4.三角形按角分类可分为锐角三角形、直角三角形和钝角三角形.【例2】(2013·东营中考)如图,已知AB∥CD,AD和BC相交于点O,∠A=50°,∠AOB=105°,则∠C等于( )
A.20° B.25° C.35° D.45°【思路点拨】根据三角形内角和定理求出∠B,再利用平行线性质定理求出∠C.
【自主解答】选B.在△AOB中,∠B=180°-∠A-∠AOB=180°-50°-105°=25°.
又∵AB∥CD,∴∠C=∠B=25°.【中考集训】
1.(2012·漳州中考)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.45° B.60° C.75° D.90°【解析】选C.由题意和图示,可以看出角α所在的三角形的其他两个内角分别是60°和45°,
所以∠α=180°-(60°+45°)=75°.2.(2013·内江中考)把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
A.125° B.120° C.140° D.130° 【解析】选D.如图,由“直角三角形两锐角互余”可知,∠3=90°-∠1=90°-40°=50°.因为直尺的对边互相平行,所以∠4=∠3=50°,所以∠2=180°-∠4=130°.3.(2013·丽水中考)如图,AB∥CD,AD和BC
相交于点O,∠A=20°,∠COD=100°,则∠C
的度数是( )
A.80° B.70° C.60° D.50°
【解析】选C.因为AB∥CD,所以∠A=∠D=20°(两直线平线,内错角相等),且∠COD=100°,所以∠C=60°.4.(2012·梅州中考)如图,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( )
A.150° B.210° C.105° D.75°【解析】选A.∵△A′DE是△ABC翻折变换而成,
∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=75°,
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-75°=105°,
∴∠1+∠2=360°-2×105°=150°.5.(2013·荆州中考)如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
A.30° B.20° C.10° D.40°【解析】选C.∵AB∥CD,∠ABE=60°,
∴∠CFB=60°,又∵∠D=50°,
∴∠E=∠CFB-∠D=60°-50°=10°.6.(2013·遂宁中考)如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 .【解析】60°角的直角三角板的另一个锐角为30°,因为∠1=18°,所以∠3=12°,再根据矩形对边平行,内错角相等可得∠2=∠3=12°.
答案:12°7.(2013·武汉模拟)已知:如图,∠B=∠C,∠1=∠2,∠BAD=40°,求∠EDC的度数.【解析】△ABD中,由三角形的外角性质知:
∠ADC=∠B+∠BAD,
即∠EDC+∠1=∠B+40° ①.
同理,得:∠2=∠EDC+∠C,
∵∠1=∠2,∠B=∠C,
∴∠1=∠EDC+∠B ②,
②代入①得:
2∠EDC+∠B=∠B+40°,
即∠EDC=20°.考点 3 多边形的内角和与外角和?
【知识点睛】
1.n边形的内角和为(n-2)·180°,外角和为360°.
2.边数每增加1,内角和就增加180°,而外角和不随边数的变化而变化,都是360°.【例3】(2012·无锡中考)若一个多边形的内角和为1080°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
【思路点拨】设元→内角和公式→方程→求解
【自主解答】选C.设这个多边形的边数为n,则
180(n-2)=1080,解得:n=8.故选C.【中考集训】
1.(2013·梅州中考)一个多边形的内角和小于它的外角和,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
【解析】选A.三角形的内角和为180°,外角和等于360°,其内角和小于外角和,四边形的内角和等于外角和,五边形、六边形的内角和大于外角和,故选A.2.(2013·资阳中考)一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形
C.正十边形 D.正十二边形
【解析】选C.360°÷36°=10.3.(2013·咸宁中考)如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( )
A.30° B.36° C.38° D.45°【解析】选B.∵正五边形的内角和为(5-2)×180°=540°,
∴正五边形的内角为540°÷5=108°,
∴∠BAE=108°.
∵AB=AE,
∴∠ABE=∠AEB=36°.
∵l∥BE,
∴∠1=∠AEB=36°.4.(2013·巴中中考)若一个多边形的内角和与外角和相等,则这个多边形是 边形.
【解析】设这个多边形的边数为n,可得(n-2)×180° =360°,解得n=4,故是四边形.
答案:四
