第六单元 平移、旋转和轴对秤单元测试(含答案)苏教版三年级上册数学
文档属性
| 名称 | 第六单元 平移、旋转和轴对秤单元测试(含答案)苏教版三年级上册数学 |
|
|
| 格式 | docx | ||
| 文件大小 | 918.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 22:09:45 | ||
图片预览

文档简介
第六单元单元测试(A卷)
时间:60分钟 满分:100分 年级 姓名
题号 一 二 三 四 五 六 七 总分
得分
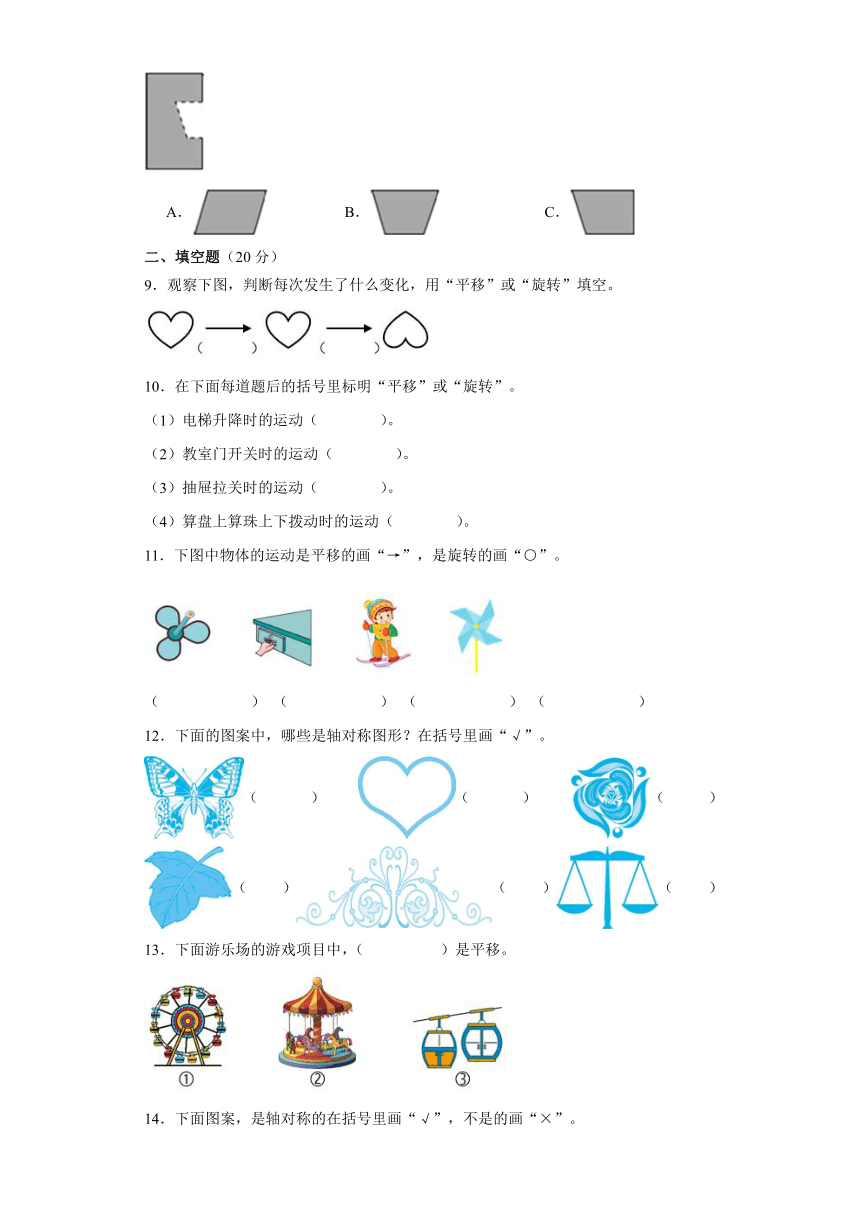
一、选择题(16分)
1.下列运动,哪一种运动方式与其它的不同?( )
A.推拉抽屉 B.荡秋千 C.转动方向盘
2.下面运动属于平移的有( )个。
①拉开抽屉 ②国旗升降 ③电梯上下 ④火车笔直前行 ⑤打开水龙头
A.2 B.3 C.4
3.下列图中,是轴对称图形的有( )个。
A.4 B.3 C.2
4.下列现象中,属于旋转的是( )。
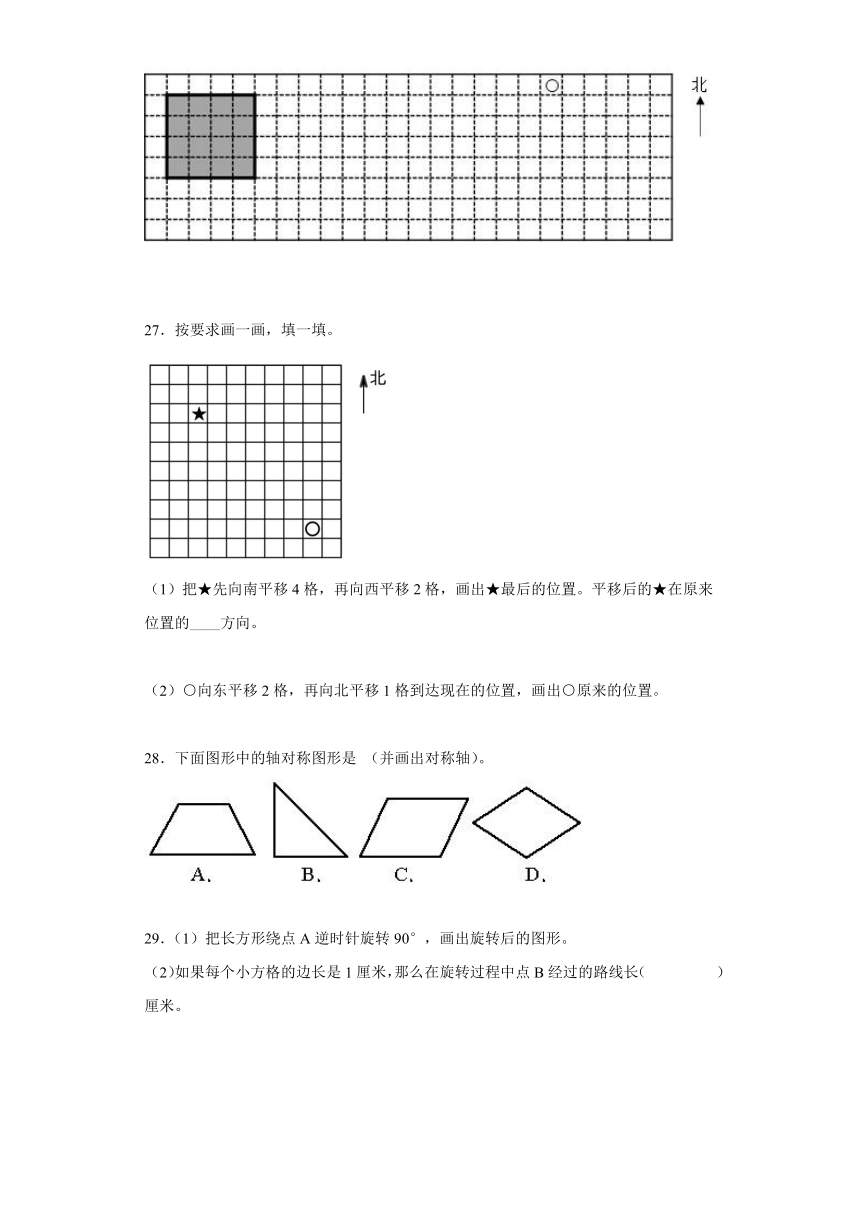
A.开关抽屉的运动 B.吊扇扇叶的运动 C.电梯的升降运动
5.将长度为9厘米的线段向上平移10厘米后,所得线段的长度是( )。
A.9厘米 B.10厘米 C.19厘米
6.如图通过平移可以和( )重合。
A. B. C.
7.如图所示的图形通过旋转后能得到下面图( )。
A. B. C.
8.将一张长方形纸对折后,沿虚线剪下一个图形(如图),剪下的图形展开后是( )。
A. B. C.
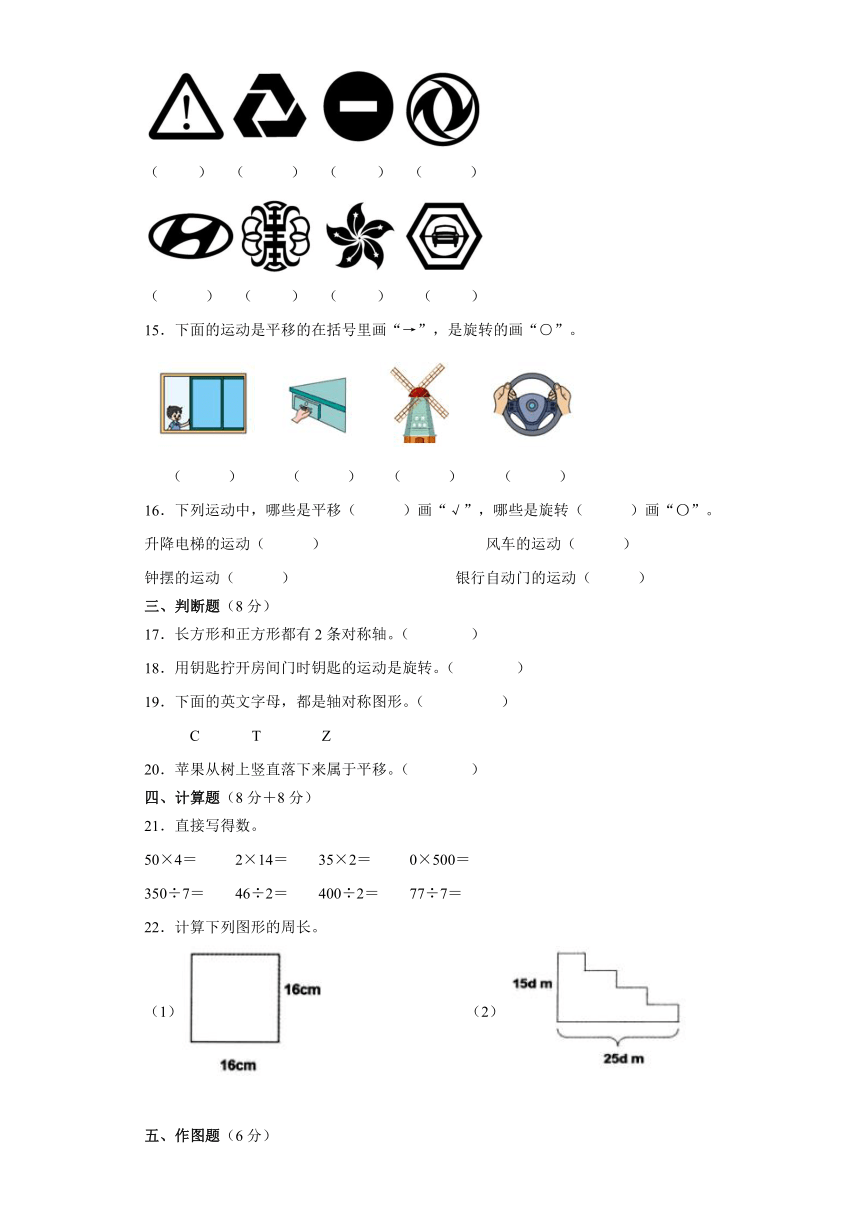
二、填空题(20分)
9.观察下图,判断每次发生了什么变化,用“平移”或“旋转”填空。
10.在下面每道题后的括号里标明“平移”或“旋转”。
(1)电梯升降时的运动( )。
(2)教室门开关时的运动( )。
(3)抽屉拉关时的运动( )。
(4)算盘上算珠上下拨动时的运动( )。
11.下图中物体的运动是平移的画“→”,是旋转的画“○”。
( ) ( ) ( ) ( )
12.下面的图案中,哪些是轴对称图形?在括号里画“√”。
( ) ( ) ( )
( )( )( )
13.下面游乐场的游戏项目中,( )是平移。
14.下面图案,是轴对称的在括号里画“√”,不是的画“×”。
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
15.下面的运动是平移的在括号里画“→”,是旋转的画“○”。
( ) ( ) ( ) ( )
16.下列运动中,哪些是平移( )画“√”,哪些是旋转( )画“〇”。
升降电梯的运动( ) 风车的运动( )
钟摆的运动( ) 银行自动门的运动( )
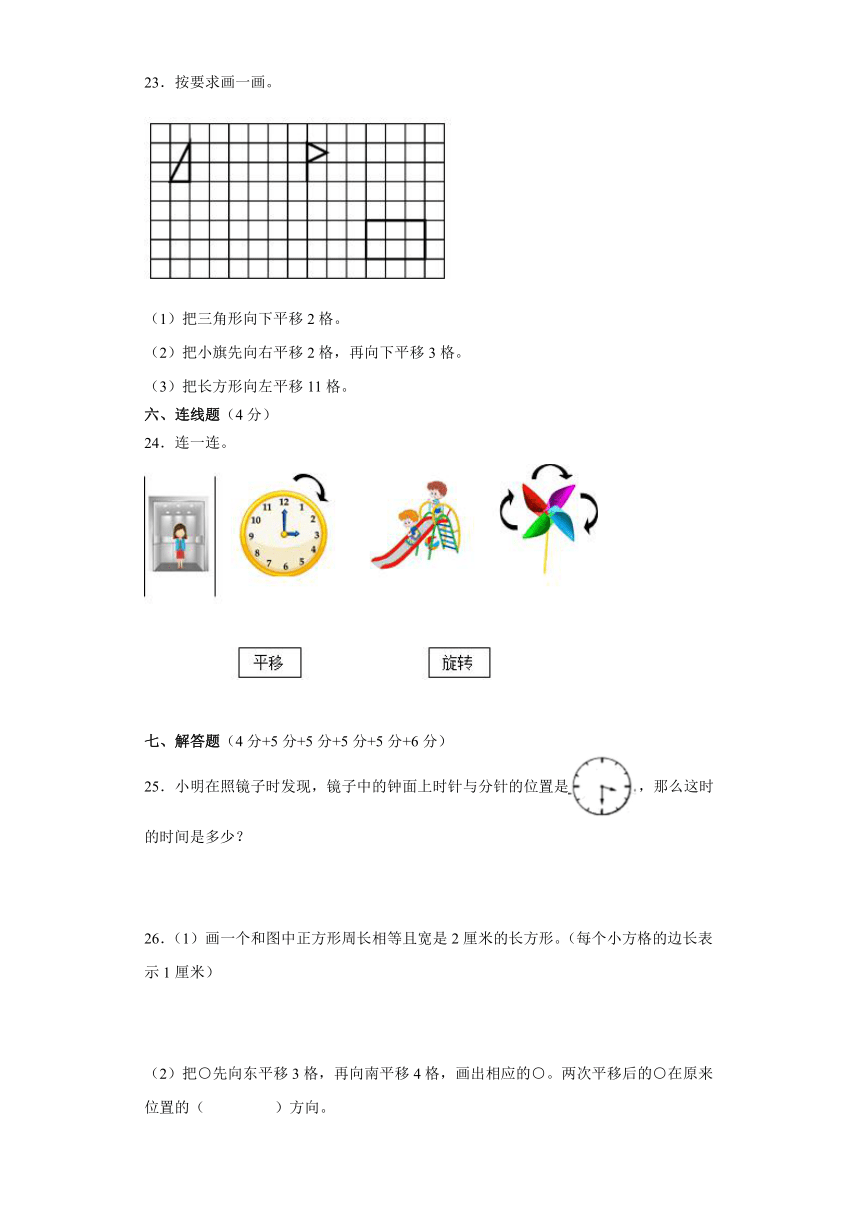
三、判断题(8分)
17.长方形和正方形都有2条对称轴。( )
18.用钥匙拧开房间门时钥匙的运动是旋转。( )
19.下面的英文字母,都是轴对称图形。( )
C T Z
20.苹果从树上竖直落下来属于平移。( )
四、计算题(8分+8分)
21.直接写得数。
50×4= 2×14= 35×2= 0×500=
350÷7= 46÷2= 400÷2= 77÷7=
22.计算下列图形的周长。
(1) (2)
五、作图题(6分)
23.按要求画一画。
(1)把三角形向下平移2格。
(2)把小旗先向右平移2格,再向下平移3格。
(3)把长方形向左平移11格。
六、连线题(4分)
24.连一连。
七、解答题(4分+5分+5分+5分+5分+6分)
25.小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是多少?
26.(1)画一个和图中正方形周长相等且宽是2厘米的长方形。(每个小方格的边长表示1厘米)
(2)把○先向东平移3格,再向南平移4格,画出相应的○。两次平移后的○在原来位置的( )方向。
27.按要求画一画,填一填。
(1)把★先向南平移4格,再向西平移2格,画出★最后的位置。平移后的★在原来位置的____方向。
(2)○向东平移2格,再向北平移1格到达现在的位置,画出○原来的位置。
28.下面图形中的轴对称图形是 (并画出对称轴)。
29.(1)把长方形绕点A逆时针旋转90°,画出旋转后的图形。
(2)如果每个小方格的边长是1厘米,那么在旋转过程中点B经过的路线长( )厘米。
30.(1)下面五个图形中,是轴对称图形的有( )。(填序号)
(2)在不是轴对称的图形上添1个小正方形,使它成为轴对称图形。
(3)在图⑤上再添2个小正方形,使新图形的周长是12厘米。(每个小方格的边长表示1厘米)
参考答案:
1.A
【分析】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
【详解】A.推拉抽屉是平移运动。
B.荡秋千是旋转运动。
C.转动方向盘是旋转运动。
故答案为:A
【点睛】本题主要考查学生对平移和旋转的特征及区别的掌握。
2.C
【分析】平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。据此解答。
【详解】①拉开抽屉、②国旗升降、③电梯上下、④火车笔直前行属于平移现象。⑤打开水龙头属于旋转现象。属于平移的有4个。
故答案为:C
【点睛】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
3.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】从左起,第1、4个图形是轴对称图形,第2、3个图形不是轴对称图形。
故答案为:C
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
4.B
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】A.开关抽屉的运动是平移;
B.吊扇扇叶的运动是旋转;
C.电梯的升降运动是平移。
吊扇扇叶的运动是旋转。
故答案为:B
5.A
【分析】将长度为9厘米的线段向上平移10厘米后,只是线段的位置发生了变化,线段的长度不变。
【详解】线段的长度还是9厘米。
故答案为:A
【点睛】平移只改变物体的位置,物体的大小、形状不变。
6.B
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。
【详解】A.方向改变,不能通过平移和重合;
B.形状、大小、方向不变,能通过平移和重合;
C.方向和位置改变,不能通过平移和重合。
故答案为:B
【点睛】此题考查了平移的意义及在实际当中的运用。
7.B
【分析】在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】通过旋转后能得到。
故答案为:B
【点睛】此题考查了旋转的意义及在实际当中的运用。
8.B
【分析】把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,称这两个图形为轴对称,据此解答。
【详解】将一张长方形纸对折后,沿虚线剪下一个图形,如图:
剪下的图形展开后是。
故答案为:B
【点睛】本题考查了轴对称的应用,看清图形的轮廓,找到对应的图形。
9.平移;旋转
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】依据分析可知:第一个图形变换到第二个图形,是平移,第二个图形变换到第三个图形是旋转。
【点睛】此题考查的是平移和旋转现象,正确区分平移和旋转是解题关键。
10.(1)平移
(2)旋转
(3)平移
(4)平移
【分析】平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的运动叫做图形的平移运动。旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转运动。
【详解】(1)电梯升降时的运动(平移)。
(2)教室门开关时的运动(旋转)。
(3)抽屉拉关时的运动(平移)。
(4)算盘上算珠上下拨动时的运动(平移)。
【点睛】熟练掌握平移和旋转的定义是解答此题的关键。
11. ○ → → ○
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】根据平移旋转的定义,是旋转,是平移,是平移,是旋转。
【点睛】此题考查了平移和旋转的意义及在实际当中的运用。
12.(√)(√)( )
( )(√)(√)
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】(√) (√) ( )
( ) (√) (√)
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
13.③
【分析】在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移。物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生了变化。
在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。物体或图形旋转后,它们的形状、大小都不改变,但是方向发生了变化。
【详解】上面游乐场的游戏项目中,①②是旋转,③是平移。
【点睛】熟练掌握平移和旋转的定义是解答此题的关键。
14. √ × √ × × √ × √
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,进行解答即可。
【详解】
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
15. → → ○ ○
【分析】平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。
旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
【详解】
【点睛】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
16. √ 〇 〇 √
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】升降电梯的运动√ 风车的运动〇
钟摆的运动〇 银行自动门的运动√
【点睛】此题考查了平移和旋转的意义及在实际当中的运用。
17.×
【分析】一个图形沿一条直线对折后,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
【详解】长方形有2条对称轴,正方形有4条对称轴,所以判断错误。
【点睛】熟练掌握常见图形对称轴的条数是解答本题的关键。
18.√
【分析】旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。据此判断即可。
【详解】根据旋转的定义可知:用钥匙拧开房间门时钥匙的运动是旋转。
故答案为:√
【点睛】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
19.×
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】Z 不是轴对称图形,C、T 是轴对称图形。
故答案为:×
【点睛】判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠。
20.√
【分析】苹果从树上竖直落下,苹果的运动轨迹是直线,据此判断。
【详解】因为苹果运动轨迹是直线,所以属于平移。
故答案为:√
【点睛】物体的平移是做直线运动。
21.200 28 70 0 50 23 200 11
【详解】略
22.(1)64厘米;(2)80分米
【分析】(1)此图为正方形,正方形的周长=边长×4,依此计算。
(2)通过平移可知:图二的周长等于长25分米,宽15分米的长方形的周长,长方形的周长=(长+宽)×2,依此计算。
【详解】(1)16×4=64(厘米)
(2)(25+15)×2
=40×2
=80(分米)
23.见详解
【分析】(1)把三角形的三个顶点分别向下平移2格,再把它们依次连接,即可画出平移后的三角形;
(2)找出小旗的关键点,把它们先向右平移2格,再向下平移3格,然后连接画出平移后的小旗;
(3)把长方形的4个顶点分别向左平移11格,再把它们依次连接即可画出平移后的长方形。
【详解】
【点睛】本题主要考查作平移后的图形。
24.见详解
【分析】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
【详解】
【点睛】熟练掌握平移与旋转的区别是解答本题的关键。
25.8:30
【分析】从镜子中看到的时刻与真实的时刻是相反的,据此解答即可。
【详解】根据镜面对称的性质可知:小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是8:30。
【点睛】掌握镜面的对称性是解题的关键。
26.(1)见详解
(2)图见详解;东南
【分析】(1)正方形的边长为4厘米,4×4÷2=8(厘米)=6厘米+2厘米,画一个长为6厘米、宽为2厘米的长方形即可。
(2)图上方位是“上北下南,左西右东”,把○先向右平移3格,再向下平移4格即可。两次平移后的○在原来位置的东南方向。
【详解】(1)
(2)图见(1),两次平移后的○在原来位置的东南方向。
【点睛】本题主要考查学生对长方形和正方形周长公式、方向的辨别、平移知识的掌握。
27.(1)西南
(1)(2)画图如下:
【分析】根据平移的特征,把★先向南平移4格,再向西平移2格,画出即可;再根据上北下南左西右东的方位,可知平移后的★在原来位置西南;
(2)根据平移的特征,将○向南移动1格,再向西平移2格,即可画出○原来的位置。
【详解】(1)把★先向南平移4格,再向西平移2格,平移后的★在原来位置的西南方向;作图如下:
(1)(2)画图如下:
【点睛】本题是考查作平移后的图形、方向与位置,作图形的平移关键看准平移的方向与格数;方向与位置是相对的,关键是观察点的选择,观察点不同,同一物体的方向也不同。
28.轴对称图形:ABD
图见详解
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答即可。
【详解】轴对称图形:ABD
29.(1)见详解
(2)4.71
【分析】(1)根据旋转的意义,找出图中长方形的4个关键处,再画出绕A按逆时针方向旋转90度后的形状即可。
(2)根据题意可知,B点所经过的路线为:以A为圆心,AB的长为半径的圆的周长的 ,利用圆的周长公式计算即可。
【详解】(1)把长方形绕点A逆时针旋转90°,如图:
(2)3.14×2×3×
=18.84×
=4.71(厘米)
【点睛】本题考查了图形的旋转变化,主要看清是顺时针还是逆时针旋转,旋转多少度,根据角度占整个圆周的多少求出经过的路线长度。
30.(1)①③⑤
(2)(3)见详解
【分析】(1)(2)如果一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此判断解答。
(3)封闭图形一周的长度叫做图形的周长;新增加两个小正方形后,计算它的周长是不是12厘米即可。
【详解】根据分析可得:
(1)五个图形中,是轴对称图形的有①③⑤;
(2)给不是轴对称图形的添1个小正方形后,成为轴对称图形,如下图所示(答案不唯一):
(3)如下图所示,在图形⑤的上边增加了2个小正方形,新图形的周长是(答案不唯一):
2+2+1+2+1+4
=4+1+2+1+4
=5+2+1+4
=7+1+4
=8+4
=12(厘米)
【点睛】本题考查的是对轴对称图形的理解,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
时间:60分钟 满分:100分 年级 姓名
题号 一 二 三 四 五 六 七 总分
得分
一、选择题(16分)
1.下列运动,哪一种运动方式与其它的不同?( )
A.推拉抽屉 B.荡秋千 C.转动方向盘
2.下面运动属于平移的有( )个。
①拉开抽屉 ②国旗升降 ③电梯上下 ④火车笔直前行 ⑤打开水龙头
A.2 B.3 C.4
3.下列图中,是轴对称图形的有( )个。
A.4 B.3 C.2
4.下列现象中,属于旋转的是( )。
A.开关抽屉的运动 B.吊扇扇叶的运动 C.电梯的升降运动
5.将长度为9厘米的线段向上平移10厘米后,所得线段的长度是( )。
A.9厘米 B.10厘米 C.19厘米
6.如图通过平移可以和( )重合。
A. B. C.
7.如图所示的图形通过旋转后能得到下面图( )。
A. B. C.
8.将一张长方形纸对折后,沿虚线剪下一个图形(如图),剪下的图形展开后是( )。
A. B. C.
二、填空题(20分)
9.观察下图,判断每次发生了什么变化,用“平移”或“旋转”填空。
10.在下面每道题后的括号里标明“平移”或“旋转”。
(1)电梯升降时的运动( )。
(2)教室门开关时的运动( )。
(3)抽屉拉关时的运动( )。
(4)算盘上算珠上下拨动时的运动( )。
11.下图中物体的运动是平移的画“→”,是旋转的画“○”。
( ) ( ) ( ) ( )
12.下面的图案中,哪些是轴对称图形?在括号里画“√”。
( ) ( ) ( )
( )( )( )
13.下面游乐场的游戏项目中,( )是平移。
14.下面图案,是轴对称的在括号里画“√”,不是的画“×”。
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
15.下面的运动是平移的在括号里画“→”,是旋转的画“○”。
( ) ( ) ( ) ( )
16.下列运动中,哪些是平移( )画“√”,哪些是旋转( )画“〇”。
升降电梯的运动( ) 风车的运动( )
钟摆的运动( ) 银行自动门的运动( )
三、判断题(8分)
17.长方形和正方形都有2条对称轴。( )
18.用钥匙拧开房间门时钥匙的运动是旋转。( )
19.下面的英文字母,都是轴对称图形。( )
C T Z
20.苹果从树上竖直落下来属于平移。( )
四、计算题(8分+8分)
21.直接写得数。
50×4= 2×14= 35×2= 0×500=
350÷7= 46÷2= 400÷2= 77÷7=
22.计算下列图形的周长。
(1) (2)
五、作图题(6分)
23.按要求画一画。
(1)把三角形向下平移2格。
(2)把小旗先向右平移2格,再向下平移3格。
(3)把长方形向左平移11格。
六、连线题(4分)
24.连一连。
七、解答题(4分+5分+5分+5分+5分+6分)
25.小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是多少?
26.(1)画一个和图中正方形周长相等且宽是2厘米的长方形。(每个小方格的边长表示1厘米)
(2)把○先向东平移3格,再向南平移4格,画出相应的○。两次平移后的○在原来位置的( )方向。
27.按要求画一画,填一填。
(1)把★先向南平移4格,再向西平移2格,画出★最后的位置。平移后的★在原来位置的____方向。
(2)○向东平移2格,再向北平移1格到达现在的位置,画出○原来的位置。
28.下面图形中的轴对称图形是 (并画出对称轴)。
29.(1)把长方形绕点A逆时针旋转90°,画出旋转后的图形。
(2)如果每个小方格的边长是1厘米,那么在旋转过程中点B经过的路线长( )厘米。
30.(1)下面五个图形中,是轴对称图形的有( )。(填序号)
(2)在不是轴对称的图形上添1个小正方形,使它成为轴对称图形。
(3)在图⑤上再添2个小正方形,使新图形的周长是12厘米。(每个小方格的边长表示1厘米)
参考答案:
1.A
【分析】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
【详解】A.推拉抽屉是平移运动。
B.荡秋千是旋转运动。
C.转动方向盘是旋转运动。
故答案为:A
【点睛】本题主要考查学生对平移和旋转的特征及区别的掌握。
2.C
【分析】平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。据此解答。
【详解】①拉开抽屉、②国旗升降、③电梯上下、④火车笔直前行属于平移现象。⑤打开水龙头属于旋转现象。属于平移的有4个。
故答案为:C
【点睛】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
3.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】从左起,第1、4个图形是轴对称图形,第2、3个图形不是轴对称图形。
故答案为:C
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
4.B
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】A.开关抽屉的运动是平移;
B.吊扇扇叶的运动是旋转;
C.电梯的升降运动是平移。
吊扇扇叶的运动是旋转。
故答案为:B
5.A
【分析】将长度为9厘米的线段向上平移10厘米后,只是线段的位置发生了变化,线段的长度不变。
【详解】线段的长度还是9厘米。
故答案为:A
【点睛】平移只改变物体的位置,物体的大小、形状不变。
6.B
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。
【详解】A.方向改变,不能通过平移和重合;
B.形状、大小、方向不变,能通过平移和重合;
C.方向和位置改变,不能通过平移和重合。
故答案为:B
【点睛】此题考查了平移的意义及在实际当中的运用。
7.B
【分析】在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】通过旋转后能得到。
故答案为:B
【点睛】此题考查了旋转的意义及在实际当中的运用。
8.B
【分析】把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,称这两个图形为轴对称,据此解答。
【详解】将一张长方形纸对折后,沿虚线剪下一个图形,如图:
剪下的图形展开后是。
故答案为:B
【点睛】本题考查了轴对称的应用,看清图形的轮廓,找到对应的图形。
9.平移;旋转
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】依据分析可知:第一个图形变换到第二个图形,是平移,第二个图形变换到第三个图形是旋转。
【点睛】此题考查的是平移和旋转现象,正确区分平移和旋转是解题关键。
10.(1)平移
(2)旋转
(3)平移
(4)平移
【分析】平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的运动叫做图形的平移运动。旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转运动。
【详解】(1)电梯升降时的运动(平移)。
(2)教室门开关时的运动(旋转)。
(3)抽屉拉关时的运动(平移)。
(4)算盘上算珠上下拨动时的运动(平移)。
【点睛】熟练掌握平移和旋转的定义是解答此题的关键。
11. ○ → → ○
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】根据平移旋转的定义,是旋转,是平移,是平移,是旋转。
【点睛】此题考查了平移和旋转的意义及在实际当中的运用。
12.(√)(√)( )
( )(√)(√)
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】(√) (√) ( )
( ) (√) (√)
【点睛】判断一个图案是否是轴对称图形的关键是看在这个图形中能否找到一条直线,使图形沿着这条直线对折后能够完全重合。
13.③
【分析】在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移。物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生了变化。
在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。物体或图形旋转后,它们的形状、大小都不改变,但是方向发生了变化。
【详解】上面游乐场的游戏项目中,①②是旋转,③是平移。
【点睛】熟练掌握平移和旋转的定义是解答此题的关键。
14. √ × √ × × √ × √
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,进行解答即可。
【详解】
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
15. → → ○ ○
【分析】平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。
旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
【详解】
【点睛】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
16. √ 〇 〇 √
【分析】在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动叫平移。平移后图形的位置改变,形状、大小、方向不变。在平面内,将一个图形绕一点按某个方向转动一定的角度,这样的运动叫做图形的旋转。旋转前后图形的位置和方向改变,形状、大小不变。
【详解】升降电梯的运动√ 风车的运动〇
钟摆的运动〇 银行自动门的运动√
【点睛】此题考查了平移和旋转的意义及在实际当中的运用。
17.×
【分析】一个图形沿一条直线对折后,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
【详解】长方形有2条对称轴,正方形有4条对称轴,所以判断错误。
【点睛】熟练掌握常见图形对称轴的条数是解答本题的关键。
18.√
【分析】旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。据此判断即可。
【详解】根据旋转的定义可知:用钥匙拧开房间门时钥匙的运动是旋转。
故答案为:√
【点睛】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
19.×
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此进行判断即可。
【详解】Z 不是轴对称图形,C、T 是轴对称图形。
故答案为:×
【点睛】判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠。
20.√
【分析】苹果从树上竖直落下,苹果的运动轨迹是直线,据此判断。
【详解】因为苹果运动轨迹是直线,所以属于平移。
故答案为:√
【点睛】物体的平移是做直线运动。
21.200 28 70 0 50 23 200 11
【详解】略
22.(1)64厘米;(2)80分米
【分析】(1)此图为正方形,正方形的周长=边长×4,依此计算。
(2)通过平移可知:图二的周长等于长25分米,宽15分米的长方形的周长,长方形的周长=(长+宽)×2,依此计算。
【详解】(1)16×4=64(厘米)
(2)(25+15)×2
=40×2
=80(分米)
23.见详解
【分析】(1)把三角形的三个顶点分别向下平移2格,再把它们依次连接,即可画出平移后的三角形;
(2)找出小旗的关键点,把它们先向右平移2格,再向下平移3格,然后连接画出平移后的小旗;
(3)把长方形的4个顶点分别向左平移11格,再把它们依次连接即可画出平移后的长方形。
【详解】
【点睛】本题主要考查作平移后的图形。
24.见详解
【分析】平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
【详解】
【点睛】熟练掌握平移与旋转的区别是解答本题的关键。
25.8:30
【分析】从镜子中看到的时刻与真实的时刻是相反的,据此解答即可。
【详解】根据镜面对称的性质可知:小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是8:30。
【点睛】掌握镜面的对称性是解题的关键。
26.(1)见详解
(2)图见详解;东南
【分析】(1)正方形的边长为4厘米,4×4÷2=8(厘米)=6厘米+2厘米,画一个长为6厘米、宽为2厘米的长方形即可。
(2)图上方位是“上北下南,左西右东”,把○先向右平移3格,再向下平移4格即可。两次平移后的○在原来位置的东南方向。
【详解】(1)
(2)图见(1),两次平移后的○在原来位置的东南方向。
【点睛】本题主要考查学生对长方形和正方形周长公式、方向的辨别、平移知识的掌握。
27.(1)西南
(1)(2)画图如下:
【分析】根据平移的特征,把★先向南平移4格,再向西平移2格,画出即可;再根据上北下南左西右东的方位,可知平移后的★在原来位置西南;
(2)根据平移的特征,将○向南移动1格,再向西平移2格,即可画出○原来的位置。
【详解】(1)把★先向南平移4格,再向西平移2格,平移后的★在原来位置的西南方向;作图如下:
(1)(2)画图如下:
【点睛】本题是考查作平移后的图形、方向与位置,作图形的平移关键看准平移的方向与格数;方向与位置是相对的,关键是观察点的选择,观察点不同,同一物体的方向也不同。
28.轴对称图形:ABD
图见详解
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答即可。
【详解】轴对称图形:ABD
29.(1)见详解
(2)4.71
【分析】(1)根据旋转的意义,找出图中长方形的4个关键处,再画出绕A按逆时针方向旋转90度后的形状即可。
(2)根据题意可知,B点所经过的路线为:以A为圆心,AB的长为半径的圆的周长的 ,利用圆的周长公式计算即可。
【详解】(1)把长方形绕点A逆时针旋转90°,如图:
(2)3.14×2×3×
=18.84×
=4.71(厘米)
【点睛】本题考查了图形的旋转变化,主要看清是顺时针还是逆时针旋转,旋转多少度,根据角度占整个圆周的多少求出经过的路线长度。
30.(1)①③⑤
(2)(3)见详解
【分析】(1)(2)如果一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;据此判断解答。
(3)封闭图形一周的长度叫做图形的周长;新增加两个小正方形后,计算它的周长是不是12厘米即可。
【详解】根据分析可得:
(1)五个图形中,是轴对称图形的有①③⑤;
(2)给不是轴对称图形的添1个小正方形后,成为轴对称图形,如下图所示(答案不唯一):
(3)如下图所示,在图形⑤的上边增加了2个小正方形,新图形的周长是(答案不唯一):
2+2+1+2+1+4
=4+1+2+1+4
=5+2+1+4
=7+1+4
=8+4
=12(厘米)
【点睛】本题考查的是对轴对称图形的理解,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
同课章节目录
- 一 两、三位数乘一位数
- 整十、整百数乘一位数的口算
- 倍的认识和有关倍的简单实际问题
- 两、三位数乘一位数(不进位)的笔算
- 两、三位数乘一位数(进位)的笔算
- 两、三位数乘一位数(连续进位)的笔算
- 乘数中间、末尾有0的乘法
- 二 千克和克
- 认识千克
- 认识克
- 三 长方形和正方形
- 长方形和正方形的基本特征
- 认识周长
- 长方形和正方形周长的计算
- 周长是多少
- 四 两、三位数除以一位数
- 两、三位数除以一位数的口算
- 两、三位数除以一位数(首位能整除)的笔算
- 除法的验算
- 两、三位数除以一位数(首位不能整除)的笔算
- 商中间、末尾有0的除法
- 五 解决问题的策略
- 间隔排列
- 六 平移、旋转和轴对称
- 七 分数的初步认识(一)
- 多彩的“分数条”
