期末模拟试卷(试题)-六年级上册数学苏教版(含解析)
文档属性
| 名称 | 期末模拟试卷(试题)-六年级上册数学苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 270.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-07 06:51:56 | ||
图片预览




文档简介
保密★启用前
期末模拟试卷-苏教版数学六年级上册
学校:___________姓名:___________ 班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.一个平行四边形的底边长24米,底是高的,和它等底等高的三角形的面积是( )平方米。
A.216 B.384 C.24
2.如图是测量一颗小铁球体积的过程。
①将400毫升的水倒进一个容量为600毫升的杯子中;
②将四颗相同的小铁球放入水中,结果水没有满;
③再将一颗同样的小铁球放入水中,结果水满溢出。
根据以上过程,推测这样一颗小铁球的体积大约在( )。
A.50立方厘米以上,60立方厘米以下
B.40立方厘米以上,50立方厘米以下
C.30立方厘米以上,40立方厘米以下
3.在含糖的糖水中加入20克糖和100克水后,糖水的含糖率比原来( )。
A.变高 B.变低 C.不变
4.一桶油漆重18千克,用去,还剩( )千克。
A. B.3 C.15
5.将一个表面涂色的正方体,切成27块大小相同的小正方体,一面涂色的有( )块。
A.6 B.8 C.16
6.拖拉机每小时耕地公顷,小时耕地( )公顷.
A.大于 B.小于 C.等于
7.一瓶可乐的商标纸上标有净含量“500mL”字样,指的是瓶子的( )。
A.表面积 B.体积 C.容积
8.在6∶7中,如果后项乘2,要使比值不变,前项应加上( )。
A.8 B.6 C.4
二、填空题
9.如图,在一个平行四边形中,丙的面积是48平方厘米,甲的面积占平行四边形面积的,甲的面积是( )平方厘米,乙的面积是( )平方厘米。
10.学校举办春季运动会,参加比赛的运动员在130~140人之间,男运动员的人数是女运动员的,男运动员有( )人,女运动员有( )人。
11.把0.35∶0.7化成最简单的整数比是( ),它的比值是( )。
12.如图,用7个完全相同的小长方形正好拼成一个大长方形,每个小长方形的长和宽的比是( ),大长方形的长和宽的比是( )。
13.一个棱长为10厘米的表面涂色的正方体,将它每条棱切分成5等份,共可切分成 个相同的小正方体,这些小正方体中,没有涂色的有( )块.
14.在括号里填上“>”“<”或“=”。
( ) ( ) ( )
15.=( )÷15=0.8=( )%=( )折。
16.学校里足球和排球的个数比是3∶4,排球的个数是篮球的,足球、排球、篮球的个数比是( ),三种球最少共有( )个。
三、判断题
17.甲数是乙数的80%,乙数就是甲数的125%.( )
18.一根钢管长米,也可以写成99%米。( )
19.冰箱的容积比它的体积小。( )
20.甲数的30%等于乙数的45%,那么甲数一定小于乙数.( )
21.a:b= ( )
22.长方体的长、宽、高都扩大到原来的2倍,表面积扩大到原来的6倍. ( )
23.一种电视机,原来每台售价10000元,现在每台售价6000元,降低了40%. ( )
四、计算题
24.直接写得数.
×= ×3= 0÷= ÷= ×=
×39= ×= ÷= ÷= ÷3=
25.计算,能简算的要简算。
()×7+ 12×()×16
5-- ()÷
26.解方程。
五、解答题
27.2020年疫情肆虐,对世界各国的经济都产生了重大的影响,然而,由于我国政府的高度重视,采取正确的措施积极应对,中国经济经过第一季度的下滑后,迅速提升,淮安市也是如此。2020年第一季度淮安市GDP总量为800亿元,第二季度比第一季度增长25%,淮安市第二季度GDP总量是多少亿元?
28.两个长方形重叠部分的面积相当于小长方形面积的,相当于大长方形面积的。如将这个图形放在桌面上,它所覆盖的桌面面积是520平方厘米。则图中大长方形的面积和小长方形的面积分别是多少平方厘米?
29.某超市运来120箱果汁,运来的牛奶箱数比果汁多.运来的牛奶比果汁多多少箱?
30.如图是由5个大小相等的正方体搭成的,它的表面积是平方米.
(1)正方体每个面的面积是多少?
(2)每个正方体的表面积是多少?
31.(长沙)甲、乙、丙三人合修一堵围墙,甲、乙合修6天完成了,乙、丙合修2天完成了余下工程的,剩下的再由甲、乙、丙三人合修5天完成,现在领工资共18000元,依工作量分配,甲、乙、丙应各得多少元?
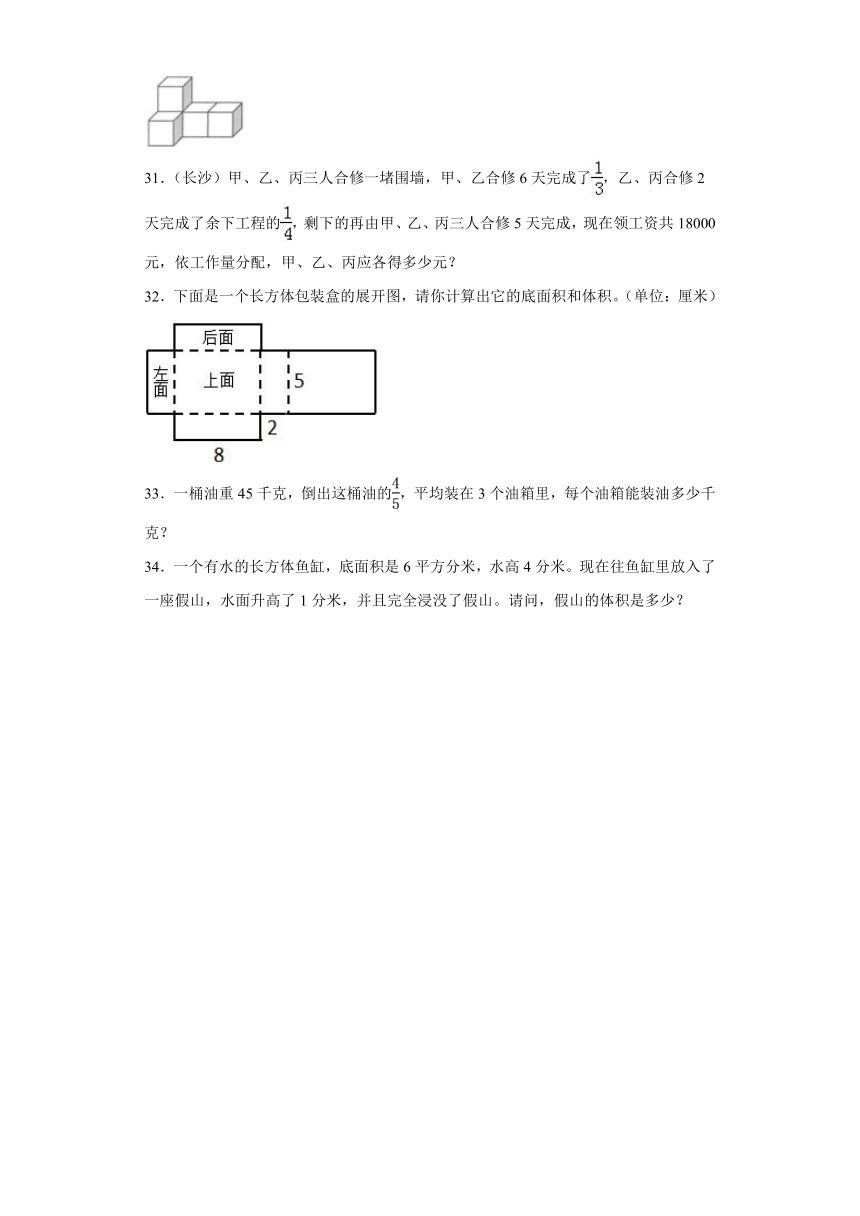
32.下面是一个长方体包装盒的展开图,请你计算出它的底面积和体积。(单位:厘米)
33.一桶油重45千克,倒出这桶油的,平均装在3个油箱里,每个油箱能装油多少千克?
34.一个有水的长方体鱼缸,底面积是6平方分米,水高4分米。现在往鱼缸里放入了一座假山,水面升高了1分米,并且完全浸没了假山。请问,假山的体积是多少?
参考答案:
1.A
【分析】把平行四边形的高看作单位“1”,根据已知一个数的几分之几是多少,求这个数,用除法求出高,等底等高的三角形的面积是平行四边形面积的一半,据此解答即可。
【详解】24÷
=24×
=18(米)
24×18÷2
=432÷2
=216(平方米)
和它等底等高的三角形的面积是216平方米。
故答案为:A
【点睛】此题考查的目的是理解掌握等底等高的三角形与平行四边形面积之间的关系及应用。
2.B
【分析】要求每颗玻璃球的体积在哪一个范围内,根据题意,四颗小铁球体积小于(600-400)毫升,因为把5颗玻璃球放入水中,结果水满溢出,五颗小铁球体积大于(600-400)毫升,据此解答即可。
【详解】600-400=200(毫升)
200÷4=50(毫升)=50(立方厘米)
200÷5=40(毫升)=40(立方厘米)
则这样一颗小铁球的体积大约在40立方厘米以上,50立方厘米以下。
故答案为:B
3.B
【分析】含糖率=×100%,先算出加入那部分的含糖率,再与原来的比较大小即可。
【详解】20÷(100+20)×100%
=20÷120×100%
≈16.7%
16.7%<20%
故答案为:B
【点睛】含糖率=×100%,注意增加糖时,糖水的重量也跟着增加。
4.B
【分析】把一桶油漆的重量看作单位“1”,已知用去,则剩下的重量占总重量的(1-),根据分数乘法的意义,用18×(1-)即可求出还剩多少千克。
【详解】18×(1-)
=18×
=3(千克)
还剩3千克。
故答案为:B
【点睛】本题主要考查了分数乘法的应用,明确求一个数的几分之几是多少,用乘法计算。
5.A
【分析】把一个表面涂色的大正方体平均分成3行,3列,3层,共27个小正方体,这些小正方体原来露在外面的面被涂色,三面涂色的在原大正方体顶点处,两面涂色的在原大正方体的每条棱长上(不包括顶点),一面涂色的在原大正方体每个面的中心,没有涂色的在原大正方体的内部,据此求出一面涂色有多少块。
【详解】(3-2)×(3-2)×6
=1×1×6
=1×6
=6(块)
将一个表面涂色的正方体,切成27块大小相同的小正方体,一面涂色的有6块。
故答案为:A
【点睛】本题考查立方体的知识,注意数形结合与正方体表面涂色的特点的应用。
6.B
【详解】试题分析:一个数乘一个小于1的数,积小于这个数.
解:由题意知,一个数乘一个小于1的数,积小于这个数,
×=,
==,
,
所以积小于公顷.
点评:此题考查了一个数乘一个小于1的数,积与这个数的关系.
7.C
【分析】容积是指木箱、油桶等所能容纳物体的体积,据此分析。
【详解】一瓶可乐的商标纸上标有净含量“500mL”字样,指的是瓶子的容积。
故答案为:C
【点睛】一个物体有体积,但它不一定有容积。
8.B
【分析】6∶7中的后项乘2,根据比的基本性质,比的前项和比的后项同时乘或除以同一个不为0的数,比值不变;所以要使比值不变,比的前项也应乘2,此时比的前项变为12,再减去6,即可求出比的前项应增加的数。
【详解】如果后项乘2,所以比的前项也应乘2;
6×2-6
=12-6
=6
所以要使比值不变,比的前项乘2或者加上6。
故答案为:B
【点睛】此题的解题关键是灵活运用比的基本性质求解。
9. 16 32
【分析】根据图可知,丙的底是平行四边形的底,丙的高是平行四边形的高,根据三角形的面积公式:底×高÷2,平行四边形的面积公式,底×高;当三角形和平行四边形等底等高时,平行四边形的面积是三角形的2倍,则平行四边形的面积是:48×2=96(平方厘米),甲的面积占平行四边形面积的,单位“1”是平行四边形的面积,单位“1”已知,用乘法,即96×=16(平方厘米),用平行四边形的面积减去甲的面积再减去丙的面积即可求出乙的面积。
【详解】48×2=96(平方厘米)
甲的面积:96×=16(平方厘米)
96-48-16=32(平方厘米)
所以甲的面积是16平方厘米;乙的面积是32平方厘米。
【点睛】本题主要考查平行四边形的面积以及三角形的面积公式的运用,同时掌握求一个数的几分之几是多少的计算方法并灵活运用。
10. 60 75
【分析】已知男运动员的人数是女运动员的,则运动员的人数应是5+4=9的倍数,又因为参加比赛的运动员在130~140人之间,所以这个数应是小于140大于130的数;
140÷9=15……5,所以人数应是9×15=135(人),用得出的总人数分别乘男、女运动员占总人数的几分之几,可分别求出男、女运动员人数。
【详解】由分析可得:
140÷9=15……5
总运动员人数为:
15×(5+4)
=15×9
=135(人)
男运动员人数:
135×
=135×
=60(人)
女运动员人数:
135×
=135×
=75(人)
综上所述:学校举办春季运动会,参加比赛的运动员在130~140人之间,男运动员的人数是女运动员的,男运动员有60人,女运动员有75人。
【点睛】解答本题的关键是先确定运动员的总人数,再根据按比例分配的方法进行解答即可。
11. 1∶2
【分析】根据比的基本性质,比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,据此化简比即可;用比的前项除以比的后项即可求出比值。
【详解】0.35∶0.7
=(0.35×100)∶(0.7×100)
=35∶70
=(35÷35)∶(70÷35)
=1∶2
1÷2=
则把0.35∶0.7化成最简单的整数比是1∶2,它的比值是。
【点睛】本题考查化简比和求比值,明确化简比和求比值的方法是解题的关键。
12. 4∶3 12∶7
【分析】假设小长方形的长是4厘米,如图所示3个小长方形长的和是12厘米刚好等于4个小长方形宽的和,则小长方形的宽等于12÷4=3厘米,所以小长方形长与宽的比是4∶3;大长方形长等于3个小长方形的长是3×4=12厘米,大长方形的宽是一个小长方形的长加上一个小长方形的宽是4+3=7厘米,则大长方形的长与宽的比是12∶7。
【详解】由分析可知:
用7个完全相同的小长方形正好拼成一个大长方形,每个小长方形的长和宽的比是4∶3,大长方形的长和宽的比是12∶7。
【点睛】此题考查了比的意义,先表示出小长方形的长、宽是解题关键。
13. 125 27
【详解】5×5×5=125(个)
没有涂色的有:
(5﹣2)×(5﹣2)×(5﹣2)
=3×3×3
=27(块)
答:共可切分成 125个相同的小正方体,这些小正方体中,没有涂色的有 27块.
故答案为125,27.
14. < > >
【分析】一个数(0除外)乘一个大于1的数,结果大于原数;一个数(0除外)乘一个小于1的数,结果小于原数;一个数(0除外)除以一个大于1的数,商就小于被除数;除以一个小于1的数商就大于被除数;据此解答。
【详解】<
>
>13,<13,所以>。
15.5;12;80;八
【分析】根据小数与分数的关系,把0.8化为分数形式,即0.8=;根据分数与除法的关系=4÷5,再根据商不变的规律,被除数和除数同时乘3就是4÷5=12÷15;把0.8的小数点向右移动两位,再加上百分号即可化为百分数,即0.8=80%;再根据几折就是百分之几十,即80%=八折。据此填空即可。
【详解】由分析可知:
=12÷15=0.8=80%=八折
16. 9∶12∶20 41
【分析】根据比与分数的关系可知:排球的个数是篮球的,也就是排球和篮球的个数比是3∶5。在3∶4和3∶5中都有排球的份数,但份数不同,不能直接连比。可以先找出排球在两个比中的两个份数的最小公倍数,然后利用比的基本性质,使其相等后,改成连比。
因为三种球的总个数为整数,即三种球的总个数是三种球个数最简整数比中各项的和的倍数,所以三种球的总个数最少是最简整数比的各项的和。
【详解】=3∶5
足球个数∶排球个数=3∶4=(3×3)∶(4×3)=9∶12
排球个数∶篮球个数=3∶5=(3×4)∶(5×4)=12∶20
所以,足球个数∶排球个数∶篮球个数=9∶12∶20。
9+12+20=41(个)
所以,足球、排球、篮球的个数比是9∶12∶20,三种球最少共有41个。
17.√
【详解】略
18.×
【分析】根据百分数表示一个数占另一个数的百分之几,也叫百分率或百分比,所以是不带单位的,据此判断。
【详解】由分析可知:百分数后面不能加单位。
故答案为:×。
【点睛】本题主要考查百分数的意义,熟练掌握百分数的意义并灵活运用。
19.√
【分析】容器的体积是指容器所占空间的大小,计算体积应该从容器的外面测量数据;容器的容积是指容器能容纳物体的内部体积,计算容积应该从容器的里面测量数据;由此进行比较即可。
【详解】由分析得:
冰箱的容积比它的体积小,这句话是正确的。
故答案为:√
【点睛】正确区分体积和容积的意义,是解决此题的关键。
20.×
【详解】(1)甲数:乙数=45%:30%=3:2,所以甲数>乙数;
(2)当甲数和乙数都等于0时,等式仍然成立,此时甲数等于乙数.
故答案为错误.
21.正确
【详解】略
22.×
【分析】长方体有6个面,都是长方形,长方体的对面相等。长方体的表面积=(长×宽+长×高+宽×高)×2。
【详解】设这个长方体的长是3厘米、宽是2厘米、高是1厘米,这个长方体的表面积是:
(3×2+3×1+2×1)×2
=(6+3+2)×2
=(9+2)×2
=11×2
=22(平方厘米)
长方体的长、宽、高都扩大到原来的2倍,则长是6厘米、宽是4厘米,高2厘米,这个长方体的表面积是:
(6×4+6×2+4×2)×2
=(24+12+8)×2
=(36+8)×2
=44×2
=88(平方厘米)
88÷22=4
故答案为:×
【点睛】采用赋值法可以较好地解决此类问题。
23.√
【详解】(10000-6000)÷10000=40% ,则降低了40%,故原题正确.
24.,,0,2,,12,,,1,.
【详解】试题分析:①分子相乘的积做分子,分母相乘的积做分母;②分子与整数相乘的积做分子,分母不变;③0除以任何数都得0;④⑧⑨⑩把除法改为乘法计算;⑤⑥⑦约分计算.
解:×=; ×3=; 0÷=0; ÷=2; ×=;
×39=12; ×=; ÷=; ÷=1; ÷3=.
故答案为,,0,2,,12,,,1,.
点评:此题考查了分数的乘法和除法以及0的特殊作用,根据题目特点,灵活解答.
25.4;248;
;3;16
【分析】(1)先运用乘法分配律,再运用加法结合律简算;
(2)(3)运用乘法分配律简算;
(4)运用加法交换律和结合律简算;
(5)根据减法的性质简算;
(6)先把除法改写成乘法,再运用乘法分配律简算。
【详解】()×7+
=
=3+()
=3+1
=4
12×()×16
=12××16+12××16
=168+80
=248
=
=×1
=
=
=1+
=
5--
=5-(+)
=5-2
=3
()÷
=()×24
=
=6-4+14
=16
26.x=2;x=;x=
【分析】(1)根据等式的性质方程两边同时加上,然后等式的两边同时除以;
(2)方程的左边计算为,然后根据等式的性质方程两边同时除以;
(3)方程的左边简化为0.4x,然后根据等式的性质方程两边同时除以0.4。
【详解】(1)
解:x-=+
x=+
x=+
x=
x÷=÷
x=×
x=2
(2)
解:x=
x÷=÷
x=÷
x=×
x=
解:40%x=48
0.4x=48
0.4x÷0.4=48÷0.4
x=120
27.1000亿元
【分析】通过题目中所说第二季度比第一季度增长25%,相当于第二季度增长了第一季度的25%,那么可以用第一季度乘25%是第二季度比第一季度增长的量,再加上第一季度的GDP总量就是第二季度GDP的总量。
【详解】800×(1+25%)
=800×125%
=1000(亿元)
答:第二季度GDP总量是1000亿元。
【点睛】本题主要考查百分数的应用题,求比一个数多百分之几的数是多少,用一个数×(1+百分之几)。
28.大长方形320平方厘米,小长方形240平方厘米
【分析】重叠部分的面积相当于小长方形面积的,相当于大长方形面积的,根据分数的意义,把小长方形的面积看作6份,大长方形的面积看作8份,重叠部分的面积是1份,则小长方形、大长方形、重叠部分的面积比是6∶8∶1。将这个图形放在桌面上,它所覆盖的桌面面积就是6+8-1=13份,则小长方形的面积占覆盖面积的,大长方形的面积占覆盖面积的,用覆盖面积分别乘和即可求出两个长方形的面积。
【详解】6+8-1=13
大长方形:520×=320(平方厘米)
小长方形:520×=240(平方厘米)
答:大长方形的面积是320平方厘米,小长方形的面积是240平方厘米。
【点睛】本题考查比的应用。根据分数的意义,得出大长方形、小长方形、重叠部分的面积比,从而求出两个长方形的面积各占覆盖面积的几分之几是解题的关键。
29.30箱
【详解】(箱)
30.(1)平方米. (2)平方米.
【详解】试题分析:(1)由题意可知:这个组合体露在外面的共有小正方体的22个面,于是用其表面积除以面的个数,即可得解;
(2)用正方体的每个面的面积乘,面的个数6,即可得解.
解:(1)÷22=(平方米);
答:正方体每个面的面积是平方米.
(2)×6=(平方米);
答:每个正方体的表面积是 平方米.
点评:此题考查了学生观察物体的能力,这个图形的表面积是图中露在外部的小正方体的面的面积之和.
31.甲、乙、丙分别应得3300元、9100元、5600元.
【详解】试题分析:要求每人分得的钱数,因为按各人所完成的工作量的多少来合理分配工资,所以必须知道每人完成的工作量.要求每人完成的工作量,就要知道每人的工作效率;由题意得甲、乙、丙工作效率之和为:[1﹣﹣(1﹣)×]÷5=,乙、丙合修2天修好余下的,乙、丙工作效率之和为:(1﹣)×÷2=,甲的工作效率为:,同理可求出乙、丙的工作效率.然后求出各自的工作量.
解答:解:甲分得的钱为:18000×{[1﹣﹣(1﹣)×]÷5﹣(1﹣)×÷2}×(6+5),
=18000×{[1﹣﹣]÷5﹣÷2}×11,
=18000×{}×11,
=3300(元);
丙分得的钱为:18000×{[1﹣﹣(1﹣)×]÷5÷6}×(2+5),
=18000×{[1﹣﹣]÷5﹣}×(2+5),
=18000×{﹣}×(2+5),
=18000××7,
=5600(元);
乙分得的钱为:18000﹣3300﹣5600=9100(元).
答:甲、乙、丙分别应得3300元、9100元、5600元.
点评:此题属于工程问题,解答此类题的关键是要知道工作量、工作时间、工作效率之间的关系.工作效率=工作量÷工作时间.
32.底面积是40平方厘米,体积是80立方厘米
【分析】由展开图可知,长方体的长是8厘米,宽是5厘米,高是2厘米,其中底面积=长×宽,体积=长×宽×高,据此代入数据计算。
【详解】底面积:8×5=40(平方厘米)
体积:8×5×2=80(立方厘米)
答:它的底面积是40平方厘米,体积是80立方厘米。
【点睛】掌握长方体的体积计算公式,找出长方体的长、宽和高是解题关键。
33.12千克
【详解】45 ×÷3=45××=12(千克)
答:每个油箱能装油12千克.
34.6立方分米
【分析】由题意知:水上升部分的体积就是假山的体积,根据长方体的体积公式:v=sh,,把数据代入计算即可。据此解答。
【详解】(立方分米)
答:假山的体积是6立方分米。
【点睛】此题主要考查长方体的体积公式在实际生活中的应用。
期末模拟试卷-苏教版数学六年级上册
学校:___________姓名:___________ 班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.一个平行四边形的底边长24米,底是高的,和它等底等高的三角形的面积是( )平方米。
A.216 B.384 C.24
2.如图是测量一颗小铁球体积的过程。
①将400毫升的水倒进一个容量为600毫升的杯子中;
②将四颗相同的小铁球放入水中,结果水没有满;
③再将一颗同样的小铁球放入水中,结果水满溢出。
根据以上过程,推测这样一颗小铁球的体积大约在( )。
A.50立方厘米以上,60立方厘米以下
B.40立方厘米以上,50立方厘米以下
C.30立方厘米以上,40立方厘米以下
3.在含糖的糖水中加入20克糖和100克水后,糖水的含糖率比原来( )。
A.变高 B.变低 C.不变
4.一桶油漆重18千克,用去,还剩( )千克。
A. B.3 C.15
5.将一个表面涂色的正方体,切成27块大小相同的小正方体,一面涂色的有( )块。
A.6 B.8 C.16
6.拖拉机每小时耕地公顷,小时耕地( )公顷.
A.大于 B.小于 C.等于
7.一瓶可乐的商标纸上标有净含量“500mL”字样,指的是瓶子的( )。
A.表面积 B.体积 C.容积
8.在6∶7中,如果后项乘2,要使比值不变,前项应加上( )。
A.8 B.6 C.4
二、填空题
9.如图,在一个平行四边形中,丙的面积是48平方厘米,甲的面积占平行四边形面积的,甲的面积是( )平方厘米,乙的面积是( )平方厘米。
10.学校举办春季运动会,参加比赛的运动员在130~140人之间,男运动员的人数是女运动员的,男运动员有( )人,女运动员有( )人。
11.把0.35∶0.7化成最简单的整数比是( ),它的比值是( )。
12.如图,用7个完全相同的小长方形正好拼成一个大长方形,每个小长方形的长和宽的比是( ),大长方形的长和宽的比是( )。
13.一个棱长为10厘米的表面涂色的正方体,将它每条棱切分成5等份,共可切分成 个相同的小正方体,这些小正方体中,没有涂色的有( )块.
14.在括号里填上“>”“<”或“=”。
( ) ( ) ( )
15.=( )÷15=0.8=( )%=( )折。
16.学校里足球和排球的个数比是3∶4,排球的个数是篮球的,足球、排球、篮球的个数比是( ),三种球最少共有( )个。
三、判断题
17.甲数是乙数的80%,乙数就是甲数的125%.( )
18.一根钢管长米,也可以写成99%米。( )
19.冰箱的容积比它的体积小。( )
20.甲数的30%等于乙数的45%,那么甲数一定小于乙数.( )
21.a:b= ( )
22.长方体的长、宽、高都扩大到原来的2倍,表面积扩大到原来的6倍. ( )
23.一种电视机,原来每台售价10000元,现在每台售价6000元,降低了40%. ( )
四、计算题
24.直接写得数.
×= ×3= 0÷= ÷= ×=
×39= ×= ÷= ÷= ÷3=
25.计算,能简算的要简算。
()×7+ 12×()×16
5-- ()÷
26.解方程。
五、解答题
27.2020年疫情肆虐,对世界各国的经济都产生了重大的影响,然而,由于我国政府的高度重视,采取正确的措施积极应对,中国经济经过第一季度的下滑后,迅速提升,淮安市也是如此。2020年第一季度淮安市GDP总量为800亿元,第二季度比第一季度增长25%,淮安市第二季度GDP总量是多少亿元?
28.两个长方形重叠部分的面积相当于小长方形面积的,相当于大长方形面积的。如将这个图形放在桌面上,它所覆盖的桌面面积是520平方厘米。则图中大长方形的面积和小长方形的面积分别是多少平方厘米?
29.某超市运来120箱果汁,运来的牛奶箱数比果汁多.运来的牛奶比果汁多多少箱?
30.如图是由5个大小相等的正方体搭成的,它的表面积是平方米.
(1)正方体每个面的面积是多少?
(2)每个正方体的表面积是多少?
31.(长沙)甲、乙、丙三人合修一堵围墙,甲、乙合修6天完成了,乙、丙合修2天完成了余下工程的,剩下的再由甲、乙、丙三人合修5天完成,现在领工资共18000元,依工作量分配,甲、乙、丙应各得多少元?
32.下面是一个长方体包装盒的展开图,请你计算出它的底面积和体积。(单位:厘米)
33.一桶油重45千克,倒出这桶油的,平均装在3个油箱里,每个油箱能装油多少千克?
34.一个有水的长方体鱼缸,底面积是6平方分米,水高4分米。现在往鱼缸里放入了一座假山,水面升高了1分米,并且完全浸没了假山。请问,假山的体积是多少?
参考答案:
1.A
【分析】把平行四边形的高看作单位“1”,根据已知一个数的几分之几是多少,求这个数,用除法求出高,等底等高的三角形的面积是平行四边形面积的一半,据此解答即可。
【详解】24÷
=24×
=18(米)
24×18÷2
=432÷2
=216(平方米)
和它等底等高的三角形的面积是216平方米。
故答案为:A
【点睛】此题考查的目的是理解掌握等底等高的三角形与平行四边形面积之间的关系及应用。
2.B
【分析】要求每颗玻璃球的体积在哪一个范围内,根据题意,四颗小铁球体积小于(600-400)毫升,因为把5颗玻璃球放入水中,结果水满溢出,五颗小铁球体积大于(600-400)毫升,据此解答即可。
【详解】600-400=200(毫升)
200÷4=50(毫升)=50(立方厘米)
200÷5=40(毫升)=40(立方厘米)
则这样一颗小铁球的体积大约在40立方厘米以上,50立方厘米以下。
故答案为:B
3.B
【分析】含糖率=×100%,先算出加入那部分的含糖率,再与原来的比较大小即可。
【详解】20÷(100+20)×100%
=20÷120×100%
≈16.7%
16.7%<20%
故答案为:B
【点睛】含糖率=×100%,注意增加糖时,糖水的重量也跟着增加。
4.B
【分析】把一桶油漆的重量看作单位“1”,已知用去,则剩下的重量占总重量的(1-),根据分数乘法的意义,用18×(1-)即可求出还剩多少千克。
【详解】18×(1-)
=18×
=3(千克)
还剩3千克。
故答案为:B
【点睛】本题主要考查了分数乘法的应用,明确求一个数的几分之几是多少,用乘法计算。
5.A
【分析】把一个表面涂色的大正方体平均分成3行,3列,3层,共27个小正方体,这些小正方体原来露在外面的面被涂色,三面涂色的在原大正方体顶点处,两面涂色的在原大正方体的每条棱长上(不包括顶点),一面涂色的在原大正方体每个面的中心,没有涂色的在原大正方体的内部,据此求出一面涂色有多少块。
【详解】(3-2)×(3-2)×6
=1×1×6
=1×6
=6(块)
将一个表面涂色的正方体,切成27块大小相同的小正方体,一面涂色的有6块。
故答案为:A
【点睛】本题考查立方体的知识,注意数形结合与正方体表面涂色的特点的应用。
6.B
【详解】试题分析:一个数乘一个小于1的数,积小于这个数.
解:由题意知,一个数乘一个小于1的数,积小于这个数,
×=,
==,
,
所以积小于公顷.
点评:此题考查了一个数乘一个小于1的数,积与这个数的关系.
7.C
【分析】容积是指木箱、油桶等所能容纳物体的体积,据此分析。
【详解】一瓶可乐的商标纸上标有净含量“500mL”字样,指的是瓶子的容积。
故答案为:C
【点睛】一个物体有体积,但它不一定有容积。
8.B
【分析】6∶7中的后项乘2,根据比的基本性质,比的前项和比的后项同时乘或除以同一个不为0的数,比值不变;所以要使比值不变,比的前项也应乘2,此时比的前项变为12,再减去6,即可求出比的前项应增加的数。
【详解】如果后项乘2,所以比的前项也应乘2;
6×2-6
=12-6
=6
所以要使比值不变,比的前项乘2或者加上6。
故答案为:B
【点睛】此题的解题关键是灵活运用比的基本性质求解。
9. 16 32
【分析】根据图可知,丙的底是平行四边形的底,丙的高是平行四边形的高,根据三角形的面积公式:底×高÷2,平行四边形的面积公式,底×高;当三角形和平行四边形等底等高时,平行四边形的面积是三角形的2倍,则平行四边形的面积是:48×2=96(平方厘米),甲的面积占平行四边形面积的,单位“1”是平行四边形的面积,单位“1”已知,用乘法,即96×=16(平方厘米),用平行四边形的面积减去甲的面积再减去丙的面积即可求出乙的面积。
【详解】48×2=96(平方厘米)
甲的面积:96×=16(平方厘米)
96-48-16=32(平方厘米)
所以甲的面积是16平方厘米;乙的面积是32平方厘米。
【点睛】本题主要考查平行四边形的面积以及三角形的面积公式的运用,同时掌握求一个数的几分之几是多少的计算方法并灵活运用。
10. 60 75
【分析】已知男运动员的人数是女运动员的,则运动员的人数应是5+4=9的倍数,又因为参加比赛的运动员在130~140人之间,所以这个数应是小于140大于130的数;
140÷9=15……5,所以人数应是9×15=135(人),用得出的总人数分别乘男、女运动员占总人数的几分之几,可分别求出男、女运动员人数。
【详解】由分析可得:
140÷9=15……5
总运动员人数为:
15×(5+4)
=15×9
=135(人)
男运动员人数:
135×
=135×
=60(人)
女运动员人数:
135×
=135×
=75(人)
综上所述:学校举办春季运动会,参加比赛的运动员在130~140人之间,男运动员的人数是女运动员的,男运动员有60人,女运动员有75人。
【点睛】解答本题的关键是先确定运动员的总人数,再根据按比例分配的方法进行解答即可。
11. 1∶2
【分析】根据比的基本性质,比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,据此化简比即可;用比的前项除以比的后项即可求出比值。
【详解】0.35∶0.7
=(0.35×100)∶(0.7×100)
=35∶70
=(35÷35)∶(70÷35)
=1∶2
1÷2=
则把0.35∶0.7化成最简单的整数比是1∶2,它的比值是。
【点睛】本题考查化简比和求比值,明确化简比和求比值的方法是解题的关键。
12. 4∶3 12∶7
【分析】假设小长方形的长是4厘米,如图所示3个小长方形长的和是12厘米刚好等于4个小长方形宽的和,则小长方形的宽等于12÷4=3厘米,所以小长方形长与宽的比是4∶3;大长方形长等于3个小长方形的长是3×4=12厘米,大长方形的宽是一个小长方形的长加上一个小长方形的宽是4+3=7厘米,则大长方形的长与宽的比是12∶7。
【详解】由分析可知:
用7个完全相同的小长方形正好拼成一个大长方形,每个小长方形的长和宽的比是4∶3,大长方形的长和宽的比是12∶7。
【点睛】此题考查了比的意义,先表示出小长方形的长、宽是解题关键。
13. 125 27
【详解】5×5×5=125(个)
没有涂色的有:
(5﹣2)×(5﹣2)×(5﹣2)
=3×3×3
=27(块)
答:共可切分成 125个相同的小正方体,这些小正方体中,没有涂色的有 27块.
故答案为125,27.
14. < > >
【分析】一个数(0除外)乘一个大于1的数,结果大于原数;一个数(0除外)乘一个小于1的数,结果小于原数;一个数(0除外)除以一个大于1的数,商就小于被除数;除以一个小于1的数商就大于被除数;据此解答。
【详解】<
>
>13,<13,所以>。
15.5;12;80;八
【分析】根据小数与分数的关系,把0.8化为分数形式,即0.8=;根据分数与除法的关系=4÷5,再根据商不变的规律,被除数和除数同时乘3就是4÷5=12÷15;把0.8的小数点向右移动两位,再加上百分号即可化为百分数,即0.8=80%;再根据几折就是百分之几十,即80%=八折。据此填空即可。
【详解】由分析可知:
=12÷15=0.8=80%=八折
16. 9∶12∶20 41
【分析】根据比与分数的关系可知:排球的个数是篮球的,也就是排球和篮球的个数比是3∶5。在3∶4和3∶5中都有排球的份数,但份数不同,不能直接连比。可以先找出排球在两个比中的两个份数的最小公倍数,然后利用比的基本性质,使其相等后,改成连比。
因为三种球的总个数为整数,即三种球的总个数是三种球个数最简整数比中各项的和的倍数,所以三种球的总个数最少是最简整数比的各项的和。
【详解】=3∶5
足球个数∶排球个数=3∶4=(3×3)∶(4×3)=9∶12
排球个数∶篮球个数=3∶5=(3×4)∶(5×4)=12∶20
所以,足球个数∶排球个数∶篮球个数=9∶12∶20。
9+12+20=41(个)
所以,足球、排球、篮球的个数比是9∶12∶20,三种球最少共有41个。
17.√
【详解】略
18.×
【分析】根据百分数表示一个数占另一个数的百分之几,也叫百分率或百分比,所以是不带单位的,据此判断。
【详解】由分析可知:百分数后面不能加单位。
故答案为:×。
【点睛】本题主要考查百分数的意义,熟练掌握百分数的意义并灵活运用。
19.√
【分析】容器的体积是指容器所占空间的大小,计算体积应该从容器的外面测量数据;容器的容积是指容器能容纳物体的内部体积,计算容积应该从容器的里面测量数据;由此进行比较即可。
【详解】由分析得:
冰箱的容积比它的体积小,这句话是正确的。
故答案为:√
【点睛】正确区分体积和容积的意义,是解决此题的关键。
20.×
【详解】(1)甲数:乙数=45%:30%=3:2,所以甲数>乙数;
(2)当甲数和乙数都等于0时,等式仍然成立,此时甲数等于乙数.
故答案为错误.
21.正确
【详解】略
22.×
【分析】长方体有6个面,都是长方形,长方体的对面相等。长方体的表面积=(长×宽+长×高+宽×高)×2。
【详解】设这个长方体的长是3厘米、宽是2厘米、高是1厘米,这个长方体的表面积是:
(3×2+3×1+2×1)×2
=(6+3+2)×2
=(9+2)×2
=11×2
=22(平方厘米)
长方体的长、宽、高都扩大到原来的2倍,则长是6厘米、宽是4厘米,高2厘米,这个长方体的表面积是:
(6×4+6×2+4×2)×2
=(24+12+8)×2
=(36+8)×2
=44×2
=88(平方厘米)
88÷22=4
故答案为:×
【点睛】采用赋值法可以较好地解决此类问题。
23.√
【详解】(10000-6000)÷10000=40% ,则降低了40%,故原题正确.
24.,,0,2,,12,,,1,.
【详解】试题分析:①分子相乘的积做分子,分母相乘的积做分母;②分子与整数相乘的积做分子,分母不变;③0除以任何数都得0;④⑧⑨⑩把除法改为乘法计算;⑤⑥⑦约分计算.
解:×=; ×3=; 0÷=0; ÷=2; ×=;
×39=12; ×=; ÷=; ÷=1; ÷3=.
故答案为,,0,2,,12,,,1,.
点评:此题考查了分数的乘法和除法以及0的特殊作用,根据题目特点,灵活解答.
25.4;248;
;3;16
【分析】(1)先运用乘法分配律,再运用加法结合律简算;
(2)(3)运用乘法分配律简算;
(4)运用加法交换律和结合律简算;
(5)根据减法的性质简算;
(6)先把除法改写成乘法,再运用乘法分配律简算。
【详解】()×7+
=
=3+()
=3+1
=4
12×()×16
=12××16+12××16
=168+80
=248
=
=×1
=
=
=1+
=
5--
=5-(+)
=5-2
=3
()÷
=()×24
=
=6-4+14
=16
26.x=2;x=;x=
【分析】(1)根据等式的性质方程两边同时加上,然后等式的两边同时除以;
(2)方程的左边计算为,然后根据等式的性质方程两边同时除以;
(3)方程的左边简化为0.4x,然后根据等式的性质方程两边同时除以0.4。
【详解】(1)
解:x-=+
x=+
x=+
x=
x÷=÷
x=×
x=2
(2)
解:x=
x÷=÷
x=÷
x=×
x=
解:40%x=48
0.4x=48
0.4x÷0.4=48÷0.4
x=120
27.1000亿元
【分析】通过题目中所说第二季度比第一季度增长25%,相当于第二季度增长了第一季度的25%,那么可以用第一季度乘25%是第二季度比第一季度增长的量,再加上第一季度的GDP总量就是第二季度GDP的总量。
【详解】800×(1+25%)
=800×125%
=1000(亿元)
答:第二季度GDP总量是1000亿元。
【点睛】本题主要考查百分数的应用题,求比一个数多百分之几的数是多少,用一个数×(1+百分之几)。
28.大长方形320平方厘米,小长方形240平方厘米
【分析】重叠部分的面积相当于小长方形面积的,相当于大长方形面积的,根据分数的意义,把小长方形的面积看作6份,大长方形的面积看作8份,重叠部分的面积是1份,则小长方形、大长方形、重叠部分的面积比是6∶8∶1。将这个图形放在桌面上,它所覆盖的桌面面积就是6+8-1=13份,则小长方形的面积占覆盖面积的,大长方形的面积占覆盖面积的,用覆盖面积分别乘和即可求出两个长方形的面积。
【详解】6+8-1=13
大长方形:520×=320(平方厘米)
小长方形:520×=240(平方厘米)
答:大长方形的面积是320平方厘米,小长方形的面积是240平方厘米。
【点睛】本题考查比的应用。根据分数的意义,得出大长方形、小长方形、重叠部分的面积比,从而求出两个长方形的面积各占覆盖面积的几分之几是解题的关键。
29.30箱
【详解】(箱)
30.(1)平方米. (2)平方米.
【详解】试题分析:(1)由题意可知:这个组合体露在外面的共有小正方体的22个面,于是用其表面积除以面的个数,即可得解;
(2)用正方体的每个面的面积乘,面的个数6,即可得解.
解:(1)÷22=(平方米);
答:正方体每个面的面积是平方米.
(2)×6=(平方米);
答:每个正方体的表面积是 平方米.
点评:此题考查了学生观察物体的能力,这个图形的表面积是图中露在外部的小正方体的面的面积之和.
31.甲、乙、丙分别应得3300元、9100元、5600元.
【详解】试题分析:要求每人分得的钱数,因为按各人所完成的工作量的多少来合理分配工资,所以必须知道每人完成的工作量.要求每人完成的工作量,就要知道每人的工作效率;由题意得甲、乙、丙工作效率之和为:[1﹣﹣(1﹣)×]÷5=,乙、丙合修2天修好余下的,乙、丙工作效率之和为:(1﹣)×÷2=,甲的工作效率为:,同理可求出乙、丙的工作效率.然后求出各自的工作量.
解答:解:甲分得的钱为:18000×{[1﹣﹣(1﹣)×]÷5﹣(1﹣)×÷2}×(6+5),
=18000×{[1﹣﹣]÷5﹣÷2}×11,
=18000×{}×11,
=3300(元);
丙分得的钱为:18000×{[1﹣﹣(1﹣)×]÷5÷6}×(2+5),
=18000×{[1﹣﹣]÷5﹣}×(2+5),
=18000×{﹣}×(2+5),
=18000××7,
=5600(元);
乙分得的钱为:18000﹣3300﹣5600=9100(元).
答:甲、乙、丙分别应得3300元、9100元、5600元.
点评:此题属于工程问题,解答此类题的关键是要知道工作量、工作时间、工作效率之间的关系.工作效率=工作量÷工作时间.
32.底面积是40平方厘米,体积是80立方厘米
【分析】由展开图可知,长方体的长是8厘米,宽是5厘米,高是2厘米,其中底面积=长×宽,体积=长×宽×高,据此代入数据计算。
【详解】底面积:8×5=40(平方厘米)
体积:8×5×2=80(立方厘米)
答:它的底面积是40平方厘米,体积是80立方厘米。
【点睛】掌握长方体的体积计算公式,找出长方体的长、宽和高是解题关键。
33.12千克
【详解】45 ×÷3=45××=12(千克)
答:每个油箱能装油12千克.
34.6立方分米
【分析】由题意知:水上升部分的体积就是假山的体积,根据长方体的体积公式:v=sh,,把数据代入计算即可。据此解答。
【详解】(立方分米)
答:假山的体积是6立方分米。
【点睛】此题主要考查长方体的体积公式在实际生活中的应用。
同课章节目录
