2015年春八下数学专题复习 第20章
文档属性
| 名称 | 2015年春八下数学专题复习 第20章 |  | |
| 格式 | zip | ||
| 文件大小 | 611.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-04 17:19:44 | ||
图片预览







文档简介
课件28张PPT。阶段专题复习
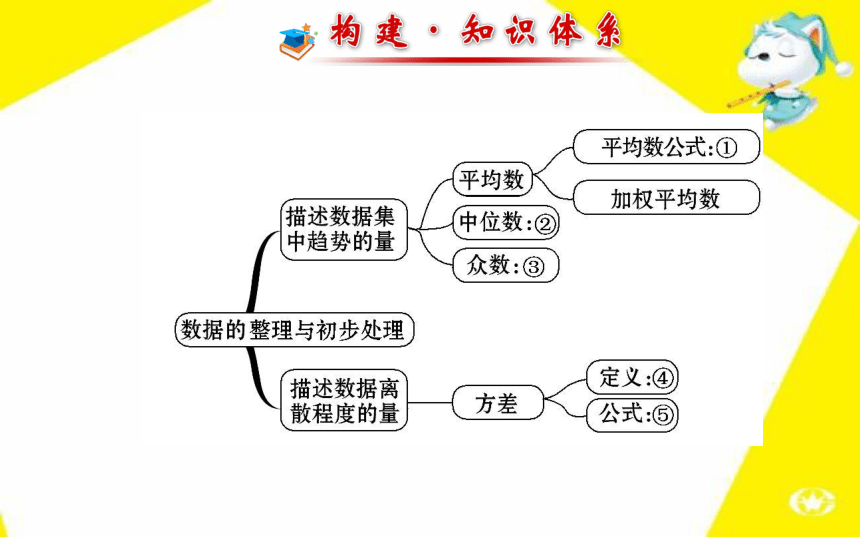
第 20 章请写出框图中数字处的内容:
①________________________________________;
②____________________________________________
___________________________;
③_____________________________;
④_________________________________;
⑤__________________________________.n个数据按大小顺序排列,处于最中间的一个数据(或最中间两个数据的平均数)一组数据中出现次数最多的数据各个数据与平均数差的平方的平均数考点 1 平均数、中位数和众数
【知识点睛】
平均数、中位数和众数的异同
1.相同点:三者从不同的角度描述一组数据的集中趋势.
2.不同点:(1)平均数与一组数据的每个数据都有关,特别是加权平均数中的“权”的不同设置会改变一组数据的平均数;中位数只与数据的排列位置有关;众数与数据出现次数的多少有关.(2)一组数据的平均数和中位数是唯一的,而众数不一定是一个. 【例1】(2012·泸州中考)“保护水资源,节约用水”应成
为每个公民的自觉行为.下表是某小区随机抽查到的10户家
庭的月用水情况,则下列关于这10户家庭的月用水量说法错
误的是( )
A.中位数是5t B.众数是5t
C.最大值与最小值的差是3t D.平均数是5.3t【思路点拨】将10个数据按大小顺序排列→
求第五个数和第六个数的平均数得中位数→
找出现次数最多的数据得众数→求加权平均数→
用最大数减最小数求出结果→作判断,得结论.【自主解答】选C.根据表格,这10个数分别是4,4,4,5,5,5,5,6,6,9,
第五个数和第六个数均为5,故中位数=
5出现次数最多,共出现4次,故众数为5.
最大数和最小数分别为9和4,故最大值与最小值的差为9-4=5,故选C.【中考集训】
1.(2013·汕头中考)数字1,2,5,3,5,3,3的中位数
是( )
A.1 B.2 C.3 D.5
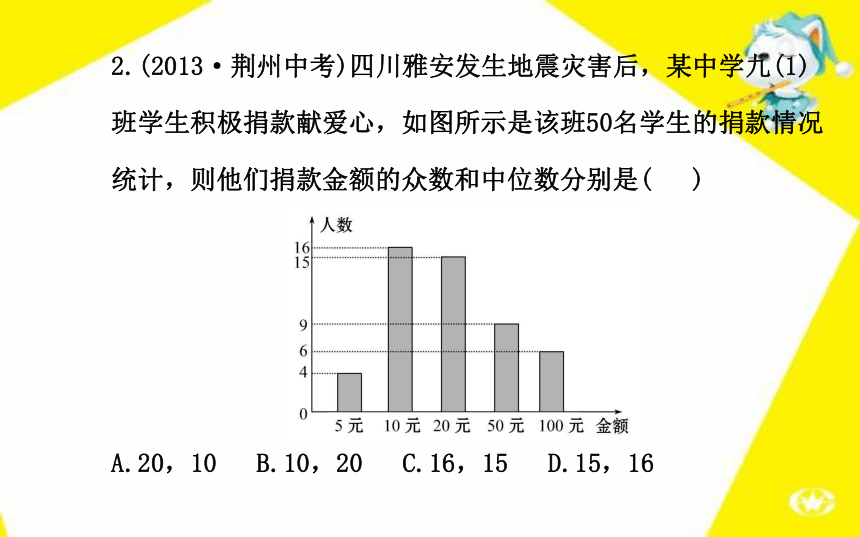
【解析】选C.将1,2,5,3,5,3,3按从小到大的顺序排列为:1,2,3,3,3,5,5.位于中间位置的数据为3,所以该组数据的中位数为3.2.(2013·荆州中考)四川雅安发生地震灾害后,某中学九(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10 B.10,20 C.16,15 D.15,16【解析】选B. 这50个数据中出现次数最多的数据是10,一
共出现了16次,所以众数是10;这50个数据按从小到大的顺
序排列,位于第25个的是20,第26个的也是20,故中位数是
=20.3.(2013·包头中考)一组数据从小到大排列为2,4,8,x,10,14,若这组数据的中位数为9,则这组数据的众数为( )
A.6 B.8 C.9 D.10
【解析】选D.因为这组从小到大排列的数的中位数是9,
所以有 =9,所以x=10,所以这组数据是2,4,8,10,
10,14,故众数是10.4.(2013·东营中考)一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是_________.
【解析】数据1,3,2,5,2,a的众数是a,所以a=2,把这
组数据由小到大排列为1,2,2,2,3,5,所以中位数是
答案:2考点 2 求方差
【知识点睛】
1.方差是反映数据离散程度的量,它越小,说明数据越稳定.
2.方差反映一组数据偏离平均值的大小.【例2】(2012·大庆中考)甲、乙两名射击运动员在某场测试中各射击20次,他们的测试成绩如下表:测试成绩比较稳定的是 .
【思路点拨】计算甲乙的加权平均数→计算甲乙的方差→结论.【自主解答】
[(7-8.5)2×4+(8-8.5)2×6+(9-8.5)2×6+(10-8.5)2×4]≈1.1,
[(7-8.5)2×6+(8-8.5)2×4+(9-8.5)2×4+(10-8.5)2×6]≈1.5.
因为
所以甲的成绩比较稳定.
答案:甲【中考集训】
1.(2013·盘锦中考)某校举行健美操比赛,甲、乙两班各
班选20名学生参加比赛,两个班参赛学生的平均身高都是
1.65米,其方差分别是 则参赛学生身高比
较整齐的班级是( )
A.甲班 B.乙班
C.同样整齐 D.无法确定
【解析】选A.∵两个班参赛学生的平均身高都是1.65米,
故参赛学生身高比较整齐的班级是甲班.2.(2013·铁岭中考)甲、乙两名射击手的50次测试的平均成
绩都是8环,方差分别是 则成绩比较稳定的是________(填“甲”或“乙”).
【解析】因为平均成绩相同,但
所以成绩比较稳定的是甲.
答案:甲3.(2013·南通中考)已知一组数据5,8,10,x,9的众数是8,那么这组数据的方差是_________.
【解析】在已知数据中,要想8是众数,则需8出现的次数最
多,也就是两次,所以x=8.即数据是5,8,10,8,9,其平
均数是 [(5-8)2+(8-8)2+…+(9-8)2]=2.8.
答案:2.84.(2013·鄂州中考)下列几个命题中正确的个数为_____个.
①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4,5,6);
②5名同学的语文成绩为90,92,92,98,103,则他们的平均分为95,众数为92;
③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定;④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清楚数据,所以对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.【解析】①由于骰子上各面点数依次为1,2,3,4,5,6,所以“掷一枚均匀骰子,朝上点数为负”为不可能事件,即该命题不正确;②根据平均数和众数的意义,可以求得他们的平均分为95、众数为92,所以该命题正确;③由于甲击中环数的方差小于乙击中环数的方差,则这一过程中甲较乙更稳定,即可得该命题不正确;④根据该部门15名员工个人年创利润统计表可知:被污渍弄脏看不清楚的数据为7,所以这组数据的中位数为第8个员工的利润,即为5万元,所以该命题不正确.所以,其中正确的命题只有1个.
答案:15.(2013·绵阳中考)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表甲、乙射击成绩折线图 (1)请补全上述图表(直接在表中填空和在图中补全折线图).
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由.
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?【解析】(1)根据折线统计图得乙的射击成绩为:2,4,6,7,7,8,8,9,9,10,
则平均数为 中位数为7.5环,
方差为 [(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+
(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4(环2).甲的射击成绩为9,6,7,6,5,6,7,9,10,平均数为7,
则甲第八环成绩为70-(9+6+7+6+5+6+7+9+10)=5(环),
成绩为5,5,6,6,6,7,7,9,9,10,
中位数为6.5,平均数为7环,
方差为 [(5-7)2+(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+
(7-7)2+(9-7)2+(9-7)2+(10-7)2]=2.8(环2),补全如下:甲、乙射击成绩统计表甲、乙射击成绩折线图
(2)由乙的方差大于甲的方差,得到甲胜出.
(3)若希望乙胜出,可以将规则定为中位数大的胜出,因为乙的中位数为7.5大于甲的中位数6.5,所以乙胜出.
第 20 章请写出框图中数字处的内容:
①________________________________________;
②____________________________________________
___________________________;
③_____________________________;
④_________________________________;
⑤__________________________________.n个数据按大小顺序排列,处于最中间的一个数据(或最中间两个数据的平均数)一组数据中出现次数最多的数据各个数据与平均数差的平方的平均数考点 1 平均数、中位数和众数
【知识点睛】
平均数、中位数和众数的异同
1.相同点:三者从不同的角度描述一组数据的集中趋势.
2.不同点:(1)平均数与一组数据的每个数据都有关,特别是加权平均数中的“权”的不同设置会改变一组数据的平均数;中位数只与数据的排列位置有关;众数与数据出现次数的多少有关.(2)一组数据的平均数和中位数是唯一的,而众数不一定是一个. 【例1】(2012·泸州中考)“保护水资源,节约用水”应成
为每个公民的自觉行为.下表是某小区随机抽查到的10户家
庭的月用水情况,则下列关于这10户家庭的月用水量说法错
误的是( )
A.中位数是5t B.众数是5t
C.最大值与最小值的差是3t D.平均数是5.3t【思路点拨】将10个数据按大小顺序排列→
求第五个数和第六个数的平均数得中位数→
找出现次数最多的数据得众数→求加权平均数→
用最大数减最小数求出结果→作判断,得结论.【自主解答】选C.根据表格,这10个数分别是4,4,4,5,5,5,5,6,6,9,
第五个数和第六个数均为5,故中位数=
5出现次数最多,共出现4次,故众数为5.
最大数和最小数分别为9和4,故最大值与最小值的差为9-4=5,故选C.【中考集训】
1.(2013·汕头中考)数字1,2,5,3,5,3,3的中位数
是( )
A.1 B.2 C.3 D.5
【解析】选C.将1,2,5,3,5,3,3按从小到大的顺序排列为:1,2,3,3,3,5,5.位于中间位置的数据为3,所以该组数据的中位数为3.2.(2013·荆州中考)四川雅安发生地震灾害后,某中学九(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10 B.10,20 C.16,15 D.15,16【解析】选B. 这50个数据中出现次数最多的数据是10,一
共出现了16次,所以众数是10;这50个数据按从小到大的顺
序排列,位于第25个的是20,第26个的也是20,故中位数是
=20.3.(2013·包头中考)一组数据从小到大排列为2,4,8,x,10,14,若这组数据的中位数为9,则这组数据的众数为( )
A.6 B.8 C.9 D.10
【解析】选D.因为这组从小到大排列的数的中位数是9,
所以有 =9,所以x=10,所以这组数据是2,4,8,10,
10,14,故众数是10.4.(2013·东营中考)一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是_________.
【解析】数据1,3,2,5,2,a的众数是a,所以a=2,把这
组数据由小到大排列为1,2,2,2,3,5,所以中位数是
答案:2考点 2 求方差
【知识点睛】
1.方差是反映数据离散程度的量,它越小,说明数据越稳定.
2.方差反映一组数据偏离平均值的大小.【例2】(2012·大庆中考)甲、乙两名射击运动员在某场测试中各射击20次,他们的测试成绩如下表:测试成绩比较稳定的是 .
【思路点拨】计算甲乙的加权平均数→计算甲乙的方差→结论.【自主解答】
[(7-8.5)2×4+(8-8.5)2×6+(9-8.5)2×6+(10-8.5)2×4]≈1.1,
[(7-8.5)2×6+(8-8.5)2×4+(9-8.5)2×4+(10-8.5)2×6]≈1.5.
因为
所以甲的成绩比较稳定.
答案:甲【中考集训】
1.(2013·盘锦中考)某校举行健美操比赛,甲、乙两班各
班选20名学生参加比赛,两个班参赛学生的平均身高都是
1.65米,其方差分别是 则参赛学生身高比
较整齐的班级是( )
A.甲班 B.乙班
C.同样整齐 D.无法确定
【解析】选A.∵两个班参赛学生的平均身高都是1.65米,
故参赛学生身高比较整齐的班级是甲班.2.(2013·铁岭中考)甲、乙两名射击手的50次测试的平均成
绩都是8环,方差分别是 则成绩比较稳定的是________(填“甲”或“乙”).
【解析】因为平均成绩相同,但
所以成绩比较稳定的是甲.
答案:甲3.(2013·南通中考)已知一组数据5,8,10,x,9的众数是8,那么这组数据的方差是_________.
【解析】在已知数据中,要想8是众数,则需8出现的次数最
多,也就是两次,所以x=8.即数据是5,8,10,8,9,其平
均数是 [(5-8)2+(8-8)2+…+(9-8)2]=2.8.
答案:2.84.(2013·鄂州中考)下列几个命题中正确的个数为_____个.
①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4,5,6);
②5名同学的语文成绩为90,92,92,98,103,则他们的平均分为95,众数为92;
③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定;④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清楚数据,所以对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.【解析】①由于骰子上各面点数依次为1,2,3,4,5,6,所以“掷一枚均匀骰子,朝上点数为负”为不可能事件,即该命题不正确;②根据平均数和众数的意义,可以求得他们的平均分为95、众数为92,所以该命题正确;③由于甲击中环数的方差小于乙击中环数的方差,则这一过程中甲较乙更稳定,即可得该命题不正确;④根据该部门15名员工个人年创利润统计表可知:被污渍弄脏看不清楚的数据为7,所以这组数据的中位数为第8个员工的利润,即为5万元,所以该命题不正确.所以,其中正确的命题只有1个.
答案:15.(2013·绵阳中考)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表甲、乙射击成绩折线图 (1)请补全上述图表(直接在表中填空和在图中补全折线图).
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由.
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?【解析】(1)根据折线统计图得乙的射击成绩为:2,4,6,7,7,8,8,9,9,10,
则平均数为 中位数为7.5环,
方差为 [(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+
(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4(环2).甲的射击成绩为9,6,7,6,5,6,7,9,10,平均数为7,
则甲第八环成绩为70-(9+6+7+6+5+6+7+9+10)=5(环),
成绩为5,5,6,6,6,7,7,9,9,10,
中位数为6.5,平均数为7环,
方差为 [(5-7)2+(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+
(7-7)2+(9-7)2+(9-7)2+(10-7)2]=2.8(环2),补全如下:甲、乙射击成绩统计表甲、乙射击成绩折线图
(2)由乙的方差大于甲的方差,得到甲胜出.
(3)若希望乙胜出,可以将规则定为中位数大的胜出,因为乙的中位数为7.5大于甲的中位数6.5,所以乙胜出.
