2015年春八下数学专题复习 第17章函数及其图象 课件
文档属性
| 名称 | 2015年春八下数学专题复习 第17章函数及其图象 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 695.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-04 17:26:47 | ||
图片预览









文档简介
课件53张PPT。阶段专题复习
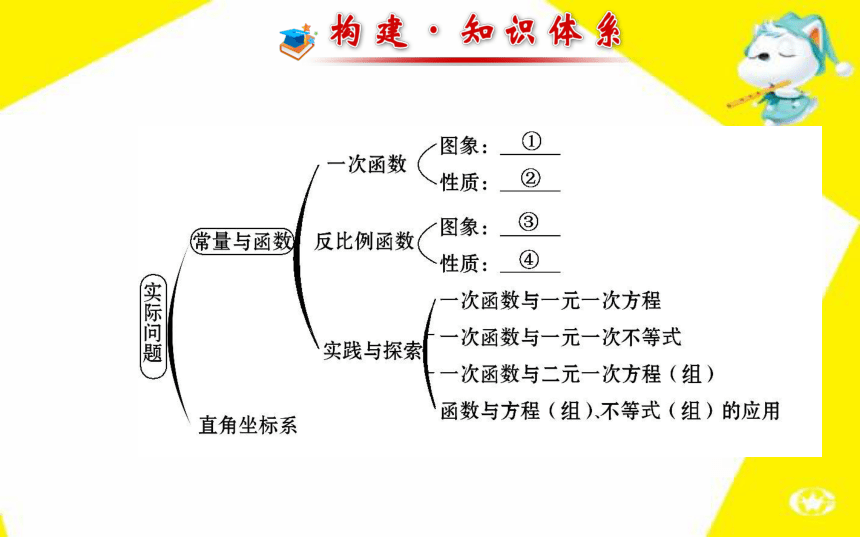
第 17 章请写出框图中数字处的内容:
①_____________________________________
_____________________;
②__________________________________________________
________________________________________________;
③_______________________________________________
_______;
④__________________________________________________
____________________________________________________
_____________.k>0时,图象经过第一、三象限,k<0时,图象经过第二、四象限k>0时,y随x的增大而增大,函数的图象从左到右上升;k<0时,y随x的增大而减小,函数的图象从左到右下降k>0时,图象在第一、三象限;k<0时,图象在第二、四象限k>0时,在每个象限内,曲线从左到右下降,y随x的增大而减小;k<0时,在每个象限内,曲线从左到右上升,y随x的增大而增大考点 1 函数的概念与图象?
【知识点睛】
1.正确区分常量与变量:常量与变量是相对于某一个过程而言的,同一个变量在不同的过程中可能是常量,也可能是变量(如温度在恒温过程中是常量,在变温过程中是变量).2.自变量取值范围的求法:①根据函数关系式的特点求.要求自变量的取值满足表示函数的代数式有意义即可;
②根据实际问题的条件或函数图象的特点求.要求自变量的取值既要使关系式有意义,还要使它表示的实际问题有意义.
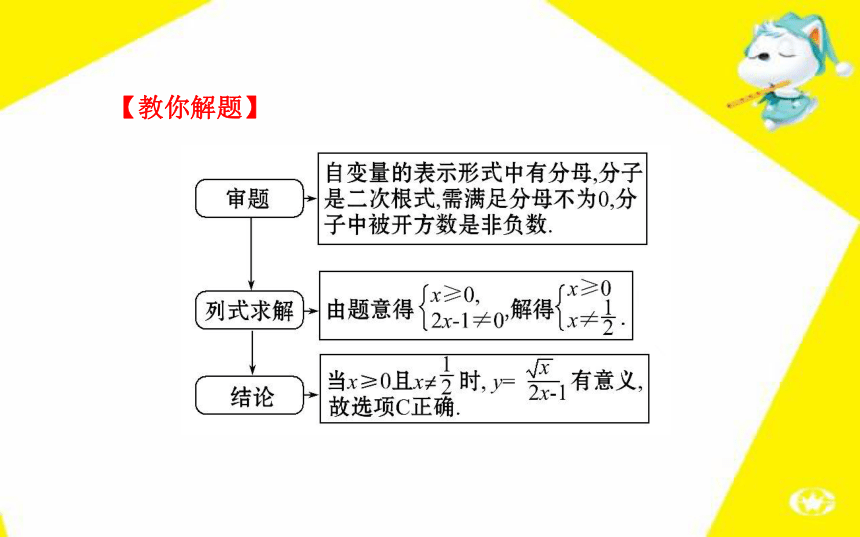
3.函数图象画法:函数图象画法的三个步骤是列表、描点、连线;特别注意画有自变量取值范围的函数图象,取点应在自变量取值范围内,画出满足条件的函数图象.【例1】(2012·徳阳中考改编)使函数y= 有意义的x的取值范围是( )
A.x≥0 B.x≠
C.x≥0且x≠ D.一切实数【教你解题】【中考集训】
1.(2013·泸州中考)函数y= 自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1
C.x≠3 D.x>1且x≠3
【解析】选A.根据题意得
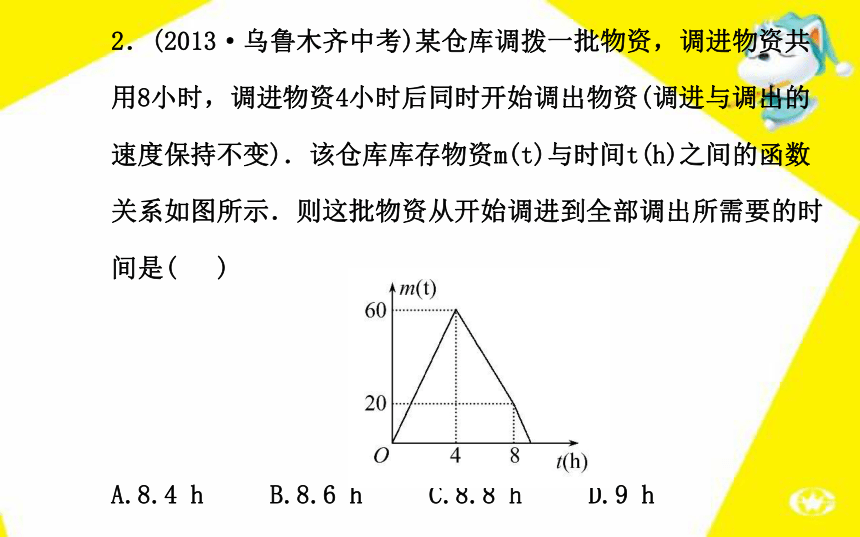
解得x≥1且x≠3.2.(2013·乌鲁木齐中考)某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(t)与时间t(h)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )
A.8.4 h B.8.6 h C.8.8 h D.9 h【解析】选C.调进物资的速度是60÷4=15(t/h),当在第
4 h时,库存物资应该有60 t,在第8 h时库存20 t,所以
调出速度是 =25(t/h),所以剩余的20 t完全
调出需要20÷25=0.8(h).
故这批物资从开始调进到全部调出需要的时间是8+0.8=8.8(h).3.(2012·万宁中考)函数y= 自变量x的取值范围
是______.【解析】根据二次根式的被开方数是非负数,分式有意义的条件是分母不等于0,
解得x≥-3且x≠1.
答案:x≥-3且x≠1考点 2 平面直角坐标系
【知识点睛】
1.象限内点的坐标特点:“一”全正,“二”负正,“三”全负,“四”正负.
2.对称点的特征:①关于x轴对称,横坐标不变,纵坐标互为相反数;②关于y轴对称,纵坐标不变,横坐标互为相反数;③关于原点对称,横、纵坐标互为相反数.
3.点到坐标轴或原点的距离:已知点(x,y),到x轴的距离
是|y|,到y轴的距离是|x|,到原点的距离是【例2】(2013·深圳中考)在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A.33 B.-33 C.-7 D.7
【思路点拨】关于原点对称→横、纵坐标互为相反数→求a,b的值→计算.
【自主解答】选D.因为P,Q关于原点对称,
所以a=-13,b=20,所以a+b=7.【中考集训】
1.(2013·湛江中考)在平面直角坐标系中,点A(2,-3)在第
________象限( )
A.一 B.二 C.三 D.四
【解析】选D.在平面直角坐标系中,点的横纵坐标的正负共同决定点所在的象限,点(+,+),(-,+),(-,-),(+,-)分别在第一、二、三、四象限.2.(2013·淮安中考)点A(-3,0)关于y轴的对称点的坐标
是______.
【解析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可知,点A(-3,0)关于y轴的对称点的坐标是(3,0).
答案:(3,0)3.(2013·宁夏中考)点P(a,a-3)在第四象限,则a的取值范围是________.
【解析】因为点P(a,a-3)在第四象限,
所以 解得0<a<3.
答案:0<a<3考点 3 一次函数的概念和性质
【知识点睛】
1.一次函数y=kx+b(k,b为常数,k≠0)的两个要点.
(1)自变量x的指数为1.(2)自变量x的系数k不为0.2.一次函数y=kx+b的五条性质.
(1)一次函数图象是一条直线,|k|的值越大,图象越靠近y轴.
(2)当k>0时,图象过一、三象限,y随x的增大而增大,从左至右图象是上升的(左低右高).
(3)当k<0时,图象过二、四象限,y随x的增大而减小,从左至右图象是下降的(左高右低).
(4)当b>0时,与y轴的交点(0,b)在正半轴;当b<0时,与y轴的交点(0,b)在负半轴;当b=0时,一次函数就是正比例函数,图象是过原点的一条直线.
(5)几条直线互相平行时,k值相等而b不相等.【例3】(2012·山西中考)如图,一次函数y=(m-1)x-3的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
A.m>1 B.m<1 C.m<0 D.m>0【思路点拨】分析图象的位置关系→确定k的取值范围→
列式求值
【自主解答】选B.由函数图象可得函数y=(m-1)x-3过二、三、四象限,即m-1<0,解得m<1,故选B.【中考集训】
1.(2013·陕西中考)如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
【解析】选D.点A的横坐标为2>0,故点A应在第一象限或第四象限;点B的纵坐标为3>0,故点B应在第一象限或第二象限;A,B两点是正比例函数图象上的两点,且不在同一象限,故点A只能在第四象限,点B只能在第二象限,从而m<0,n<0.2.(2013·泰安中考)把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
A.1C.m>1 D.m<4
【解析】选A.把直线y=-x-3向上平移m个单位后,直线关系式为y=-x-3+m,当x=0时,y=2x+4=4,即直线y=2x+4与y轴交点为(0,4),当y=0时,0=2x+4,x=-2,即直线y=2x+4与x轴交点为(-2,0),将(0,4),(-2,0)分别代入y=-x-3+m,解得m=7,m=1,所以1所以y=- x+50,
根据三角形的三边关系,x>y-y=0,
x<y+y=2y,
所以x+x<100,
解得x<50,
所以,y与x的函数关系式为y=- x+50(0<x<50),
纵观各选项,只有C选项符合.考点 4 一次函数表达式的确定及应用
【知识点睛】
1.待定系数法确定一次函数表达式的四个步骤.
(1)设,设出一次函数的一般形式.
(2)列,根据条件列出方程或方程组.
(3)解,解方程或方程组求出待定系数的值.
(4)写出一次函数的表达式.2.应用一次函数解决问题的三个步骤.
(1)分析问题:一种类型是从情境中或借助图、表等手段分析题目中的数量关系, 从而确定函数表达式;再一种类型是根据函数图象,获取信息分析数量关系.
(2)确定模型:根据获取到的信息确定一次函数模型.
(3)解决问题:根据题目中的数量关系或者数学模型,将具体数字代入,从而解决问题.【例4】(2012·衢州中考)在社会主义
新农村建设中,衢州某乡镇决定对A,
B两村之间的公路进行改造,并由甲工
程队从A村向B村方向修筑,乙工程队
从B村向A村方向修筑.已知甲工程队先
施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲、乙两个工程队修公路的长度y(米)与施工时间 x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间 x(天)之间的函数表达式.
(3)若该工程由甲、乙两工程队一直合作施工,需几天完成?【思路点拨】分析函数图象→列出函数表达式→
待定系数法求表达式→对比、计算
【自主解答】(1)∵720÷(9-3)=120,
∴乙工程队每天修公路120米. (2)设y乙=kx+b,则
∴ ∴y乙=120x-360.
当x=6时,y乙=360.
设y甲=kx,则360=6k,k=60,∴y甲=60x.
(3)当x=15时,y甲=900,
∴该公路总长为:720+900=1 620(米).
设需x天完成,由题意得,(120+60)x=1 620,
解得x=9.
答:需9天完成.【中考集训】
1.(2012·湛江中考)某市实施“农业立市,工业强市,旅游兴市”计划后,2009年全市荔枝种植面积为24万亩.调查分析结果显示,从2009年开始,该市荔枝种植面积y(万亩)随着时间x(年)逐年成直线上升,y与x之间的函数关系如图所示.(1)求y与x之间的函数表达式(不必注明自变量x的取值范围).
(2)该市2012年荔枝种植面积为多少万亩?【解析】(1)由图象可知函数图象经过点(2 009,24)和
(2 011,26),
设函数的表达式为y=kx+b,
解得
∴y与x之间的表达式为y=x-1 985.
(2)令x=2 012,
∴y=2 012-1 985=27,
∴该市2012年荔枝种植面积为27万亩.2.(2013·绍兴中考)某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数表达式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.【解析】(1)由图象得:
出租车的起步价是8元;
设当x>3时,y与x的函数表达式为y=kx+b,
由函数图象,得
故y与x的函数表达式为y=2x+2.
(2)当y=32时,32=2x+2,
x=15.
答:这位乘客乘车的里程是15 km.考点 5 反比例函数的图象与性质
【知识点睛】
1.反比例函数y= (k为常数,k≠0)的图象是双曲线.
2.当k>0,双曲线的两支分别位于第一、三象限,在每一象限内y随x的增大而减小.
3.当k<0,双曲线的两支分别位于第二、四象限,在每一象限内y随x的增大而增大.【例5】(2012·济宁中考)如图是反比例函数y= 的图象的一个分支,对于给出的下列说法: ①常数k的取值范围是k>2;
②另一个分支在第三象限;
③在函数图象上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1④在函数图象的某一个分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1其中正确的是 (在横线上填出正确的序号).【思路点拨】分析函数图象→明确k-2的取值
→利用k的符号作出判断
【自主解答】由图象知,k-2>0,所以k>2,①正确;反比例函数的图象在一,三象限或二,四象限,所以②正确;若A,B在不同的分支,则③不正确;在同一分支上,则一定正确,故④正确.
答案:①②④【中考集训】
1.(2013·随州中考)正比例函数y=kx和反比例函数y=
(k是常数且k≠0)在同一平面直角坐标系中的图象可能是( )【解析】选C.∵正比例函数y=kx过原点,∴B错误,又因为
k2+1>0,-(k2+1)<0,根据反比例函数图象的分布情况,y=
的图象应分布在二、四象限,故选C.2.(2013·衢州中考)若函数y= 的图象在其所在的每一
象限内,函数值y随自变量x的增大而增大,则m的取值范围
是( )
A.m<-2 B.m<0
C.m>-2 D.m>0
【解析】选A.由反比例函数的性质:在每一象限内,函数值y随自变量x的增大而增大时,m+2<0,解得m<-2.3.(2013·漳州中考)如图,反比例函数y= 的图象经过点P,则k=________.
【解析】k=3×(-2)=-6.
答案:-64.(2013·达州中考)点(x1,y1),(x2,y2)在反比例函数
y= 的图象上,当x1 (只填一个符合条件的k的值即可)
【解析】在每一个象限内,y随x的增大而增大,
所以k<0.
答案:-1(答案不唯一)考点 6 反比例函数在实际生活中的应用?
【知识点睛】
利用反比例函数解决实际问题用到的数学思想
1.数学建模思想:建立反比例函数关系模型来表示问题中的数量关系.
2.数形结合思想:从图象中获取所需信息.
3.转化思想:将实际问题转化成数学问题来求解.
4.方程思想:根据条件列出方程求解.【例6】(2013·益阳中考)我市某蔬菜生产基地在气温较低
时,用装有恒温系统的大棚栽培一种在自然光照且温度为
18℃的条件下生长最快的新品种.如图是某天恒温系统从开
启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的
函数图象,其中BC段是双曲线y= 的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值.
(3)当x=16时,大棚内的温度约为多少℃?【思路点拨】(1)观察图象,求出时间.
(2)把点B的坐标代入求k.
(3)把x=16代入y= ,求出对应的y.【自主解答】(1)恒温系统在这天保持大棚温度18 ℃的时间为10小时.
(2)∵点B(12,18)在双曲线y= 上,
∴18= ,∴k=216.
(3)当x=16时,y= =13.5,
所以当x=16时,大棚内的温度约为13.5 ℃.【中考集训】
1.(2013·青岛中考)已知矩形的面积为36cm2,相邻两条边长分别为xcm和ycm,则y与x之间的函数图象大致是( )【解析】选A.依题意,xy=36,∴y= ,其图象为位于一、三象限的双曲线,且y随x的增大而减小.
又∵矩形边长x>0,所以图象为第一象限的一个分支.2.(2012·宜昌中考)蓄电池的电压为定值.使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的关系式.
(2)当R=10Ω时,电流能是4 A吗?为什么?【解析】(1)电流I(A)是电阻R(Ω)的反比例函数,
设I= (k≠0),把(4,9)代入得:k=4×9=36,
∴I= (R>0).
(2)方法一:当R=10 Ω时,I=3.6≠4,
∴电流不可能是4 A.
方法二:∵10×4=40≠36,
∴当R=10 Ω时,电流不可能是4 A.
第 17 章请写出框图中数字处的内容:
①_____________________________________
_____________________;
②__________________________________________________
________________________________________________;
③_______________________________________________
_______;
④__________________________________________________
____________________________________________________
_____________.k>0时,图象经过第一、三象限,k<0时,图象经过第二、四象限k>0时,y随x的增大而增大,函数的图象从左到右上升;k<0时,y随x的增大而减小,函数的图象从左到右下降k>0时,图象在第一、三象限;k<0时,图象在第二、四象限k>0时,在每个象限内,曲线从左到右下降,y随x的增大而减小;k<0时,在每个象限内,曲线从左到右上升,y随x的增大而增大考点 1 函数的概念与图象?
【知识点睛】
1.正确区分常量与变量:常量与变量是相对于某一个过程而言的,同一个变量在不同的过程中可能是常量,也可能是变量(如温度在恒温过程中是常量,在变温过程中是变量).2.自变量取值范围的求法:①根据函数关系式的特点求.要求自变量的取值满足表示函数的代数式有意义即可;
②根据实际问题的条件或函数图象的特点求.要求自变量的取值既要使关系式有意义,还要使它表示的实际问题有意义.
3.函数图象画法:函数图象画法的三个步骤是列表、描点、连线;特别注意画有自变量取值范围的函数图象,取点应在自变量取值范围内,画出满足条件的函数图象.【例1】(2012·徳阳中考改编)使函数y= 有意义的x的取值范围是( )
A.x≥0 B.x≠
C.x≥0且x≠ D.一切实数【教你解题】【中考集训】
1.(2013·泸州中考)函数y= 自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1
C.x≠3 D.x>1且x≠3
【解析】选A.根据题意得
解得x≥1且x≠3.2.(2013·乌鲁木齐中考)某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(t)与时间t(h)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )
A.8.4 h B.8.6 h C.8.8 h D.9 h【解析】选C.调进物资的速度是60÷4=15(t/h),当在第
4 h时,库存物资应该有60 t,在第8 h时库存20 t,所以
调出速度是 =25(t/h),所以剩余的20 t完全
调出需要20÷25=0.8(h).
故这批物资从开始调进到全部调出需要的时间是8+0.8=8.8(h).3.(2012·万宁中考)函数y= 自变量x的取值范围
是______.【解析】根据二次根式的被开方数是非负数,分式有意义的条件是分母不等于0,
解得x≥-3且x≠1.
答案:x≥-3且x≠1考点 2 平面直角坐标系
【知识点睛】
1.象限内点的坐标特点:“一”全正,“二”负正,“三”全负,“四”正负.
2.对称点的特征:①关于x轴对称,横坐标不变,纵坐标互为相反数;②关于y轴对称,纵坐标不变,横坐标互为相反数;③关于原点对称,横、纵坐标互为相反数.
3.点到坐标轴或原点的距离:已知点(x,y),到x轴的距离
是|y|,到y轴的距离是|x|,到原点的距离是【例2】(2013·深圳中考)在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为( )
A.33 B.-33 C.-7 D.7
【思路点拨】关于原点对称→横、纵坐标互为相反数→求a,b的值→计算.
【自主解答】选D.因为P,Q关于原点对称,
所以a=-13,b=20,所以a+b=7.【中考集训】
1.(2013·湛江中考)在平面直角坐标系中,点A(2,-3)在第
________象限( )
A.一 B.二 C.三 D.四
【解析】选D.在平面直角坐标系中,点的横纵坐标的正负共同决定点所在的象限,点(+,+),(-,+),(-,-),(+,-)分别在第一、二、三、四象限.2.(2013·淮安中考)点A(-3,0)关于y轴的对称点的坐标
是______.
【解析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可知,点A(-3,0)关于y轴的对称点的坐标是(3,0).
答案:(3,0)3.(2013·宁夏中考)点P(a,a-3)在第四象限,则a的取值范围是________.
【解析】因为点P(a,a-3)在第四象限,
所以 解得0<a<3.
答案:0<a<3考点 3 一次函数的概念和性质
【知识点睛】
1.一次函数y=kx+b(k,b为常数,k≠0)的两个要点.
(1)自变量x的指数为1.(2)自变量x的系数k不为0.2.一次函数y=kx+b的五条性质.
(1)一次函数图象是一条直线,|k|的值越大,图象越靠近y轴.
(2)当k>0时,图象过一、三象限,y随x的增大而增大,从左至右图象是上升的(左低右高).
(3)当k<0时,图象过二、四象限,y随x的增大而减小,从左至右图象是下降的(左高右低).
(4)当b>0时,与y轴的交点(0,b)在正半轴;当b<0时,与y轴的交点(0,b)在负半轴;当b=0时,一次函数就是正比例函数,图象是过原点的一条直线.
(5)几条直线互相平行时,k值相等而b不相等.【例3】(2012·山西中考)如图,一次函数y=(m-1)x-3的图象分别与x轴、y轴的负半轴相交于A,B,则m的取值范围是( )
A.m>1 B.m<1 C.m<0 D.m>0【思路点拨】分析图象的位置关系→确定k的取值范围→
列式求值
【自主解答】选B.由函数图象可得函数y=(m-1)x-3过二、三、四象限,即m-1<0,解得m<1,故选B.【中考集训】
1.(2013·陕西中考)如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
【解析】选D.点A的横坐标为2>0,故点A应在第一象限或第四象限;点B的纵坐标为3>0,故点B应在第一象限或第二象限;A,B两点是正比例函数图象上的两点,且不在同一象限,故点A只能在第四象限,点B只能在第二象限,从而m<0,n<0.2.(2013·泰安中考)把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m的取值范围是( )
A.1
【解析】选A.把直线y=-x-3向上平移m个单位后,直线关系式为y=-x-3+m,当x=0时,y=2x+4=4,即直线y=2x+4与y轴交点为(0,4),当y=0时,0=2x+4,x=-2,即直线y=2x+4与x轴交点为(-2,0),将(0,4),(-2,0)分别代入y=-x-3+m,解得m=7,m=1,所以1
根据三角形的三边关系,x>y-y=0,
x<y+y=2y,
所以x+x<100,
解得x<50,
所以,y与x的函数关系式为y=- x+50(0<x<50),
纵观各选项,只有C选项符合.考点 4 一次函数表达式的确定及应用
【知识点睛】
1.待定系数法确定一次函数表达式的四个步骤.
(1)设,设出一次函数的一般形式.
(2)列,根据条件列出方程或方程组.
(3)解,解方程或方程组求出待定系数的值.
(4)写出一次函数的表达式.2.应用一次函数解决问题的三个步骤.
(1)分析问题:一种类型是从情境中或借助图、表等手段分析题目中的数量关系, 从而确定函数表达式;再一种类型是根据函数图象,获取信息分析数量关系.
(2)确定模型:根据获取到的信息确定一次函数模型.
(3)解决问题:根据题目中的数量关系或者数学模型,将具体数字代入,从而解决问题.【例4】(2012·衢州中考)在社会主义
新农村建设中,衢州某乡镇决定对A,
B两村之间的公路进行改造,并由甲工
程队从A村向B村方向修筑,乙工程队
从B村向A村方向修筑.已知甲工程队先
施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲、乙两个工程队修公路的长度y(米)与施工时间 x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间 x(天)之间的函数表达式.
(3)若该工程由甲、乙两工程队一直合作施工,需几天完成?【思路点拨】分析函数图象→列出函数表达式→
待定系数法求表达式→对比、计算
【自主解答】(1)∵720÷(9-3)=120,
∴乙工程队每天修公路120米. (2)设y乙=kx+b,则
∴ ∴y乙=120x-360.
当x=6时,y乙=360.
设y甲=kx,则360=6k,k=60,∴y甲=60x.
(3)当x=15时,y甲=900,
∴该公路总长为:720+900=1 620(米).
设需x天完成,由题意得,(120+60)x=1 620,
解得x=9.
答:需9天完成.【中考集训】
1.(2012·湛江中考)某市实施“农业立市,工业强市,旅游兴市”计划后,2009年全市荔枝种植面积为24万亩.调查分析结果显示,从2009年开始,该市荔枝种植面积y(万亩)随着时间x(年)逐年成直线上升,y与x之间的函数关系如图所示.(1)求y与x之间的函数表达式(不必注明自变量x的取值范围).
(2)该市2012年荔枝种植面积为多少万亩?【解析】(1)由图象可知函数图象经过点(2 009,24)和
(2 011,26),
设函数的表达式为y=kx+b,
解得
∴y与x之间的表达式为y=x-1 985.
(2)令x=2 012,
∴y=2 012-1 985=27,
∴该市2012年荔枝种植面积为27万亩.2.(2013·绍兴中考)某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数表达式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.【解析】(1)由图象得:
出租车的起步价是8元;
设当x>3时,y与x的函数表达式为y=kx+b,
由函数图象,得
故y与x的函数表达式为y=2x+2.
(2)当y=32时,32=2x+2,
x=15.
答:这位乘客乘车的里程是15 km.考点 5 反比例函数的图象与性质
【知识点睛】
1.反比例函数y= (k为常数,k≠0)的图象是双曲线.
2.当k>0,双曲线的两支分别位于第一、三象限,在每一象限内y随x的增大而减小.
3.当k<0,双曲线的两支分别位于第二、四象限,在每一象限内y随x的增大而增大.【例5】(2012·济宁中考)如图是反比例函数y= 的图象的一个分支,对于给出的下列说法: ①常数k的取值范围是k>2;
②另一个分支在第三象限;
③在函数图象上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1
→利用k的符号作出判断
【自主解答】由图象知,k-2>0,所以k>2,①正确;反比例函数的图象在一,三象限或二,四象限,所以②正确;若A,B在不同的分支,则③不正确;在同一分支上,则一定正确,故④正确.
答案:①②④【中考集训】
1.(2013·随州中考)正比例函数y=kx和反比例函数y=
(k是常数且k≠0)在同一平面直角坐标系中的图象可能是( )【解析】选C.∵正比例函数y=kx过原点,∴B错误,又因为
k2+1>0,-(k2+1)<0,根据反比例函数图象的分布情况,y=
的图象应分布在二、四象限,故选C.2.(2013·衢州中考)若函数y= 的图象在其所在的每一
象限内,函数值y随自变量x的增大而增大,则m的取值范围
是( )
A.m<-2 B.m<0
C.m>-2 D.m>0
【解析】选A.由反比例函数的性质:在每一象限内,函数值y随自变量x的增大而增大时,m+2<0,解得m<-2.3.(2013·漳州中考)如图,反比例函数y= 的图象经过点P,则k=________.
【解析】k=3×(-2)=-6.
答案:-64.(2013·达州中考)点(x1,y1),(x2,y2)在反比例函数
y= 的图象上,当x1
【解析】在每一个象限内,y随x的增大而增大,
所以k<0.
答案:-1(答案不唯一)考点 6 反比例函数在实际生活中的应用?
【知识点睛】
利用反比例函数解决实际问题用到的数学思想
1.数学建模思想:建立反比例函数关系模型来表示问题中的数量关系.
2.数形结合思想:从图象中获取所需信息.
3.转化思想:将实际问题转化成数学问题来求解.
4.方程思想:根据条件列出方程求解.【例6】(2013·益阳中考)我市某蔬菜生产基地在气温较低
时,用装有恒温系统的大棚栽培一种在自然光照且温度为
18℃的条件下生长最快的新品种.如图是某天恒温系统从开
启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的
函数图象,其中BC段是双曲线y= 的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值.
(3)当x=16时,大棚内的温度约为多少℃?【思路点拨】(1)观察图象,求出时间.
(2)把点B的坐标代入求k.
(3)把x=16代入y= ,求出对应的y.【自主解答】(1)恒温系统在这天保持大棚温度18 ℃的时间为10小时.
(2)∵点B(12,18)在双曲线y= 上,
∴18= ,∴k=216.
(3)当x=16时,y= =13.5,
所以当x=16时,大棚内的温度约为13.5 ℃.【中考集训】
1.(2013·青岛中考)已知矩形的面积为36cm2,相邻两条边长分别为xcm和ycm,则y与x之间的函数图象大致是( )【解析】选A.依题意,xy=36,∴y= ,其图象为位于一、三象限的双曲线,且y随x的增大而减小.
又∵矩形边长x>0,所以图象为第一象限的一个分支.2.(2012·宜昌中考)蓄电池的电压为定值.使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的关系式.
(2)当R=10Ω时,电流能是4 A吗?为什么?【解析】(1)电流I(A)是电阻R(Ω)的反比例函数,
设I= (k≠0),把(4,9)代入得:k=4×9=36,
∴I= (R>0).
(2)方法一:当R=10 Ω时,I=3.6≠4,
∴电流不可能是4 A.
方法二:∵10×4=40≠36,
∴当R=10 Ω时,电流不可能是4 A.
