2015年春八下数学专题复习 第18章平行四边形 课件
文档属性
| 名称 | 2015年春八下数学专题复习 第18章平行四边形 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 512.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-04 17:28:13 | ||
图片预览







文档简介
课件23张PPT。阶段专题复习
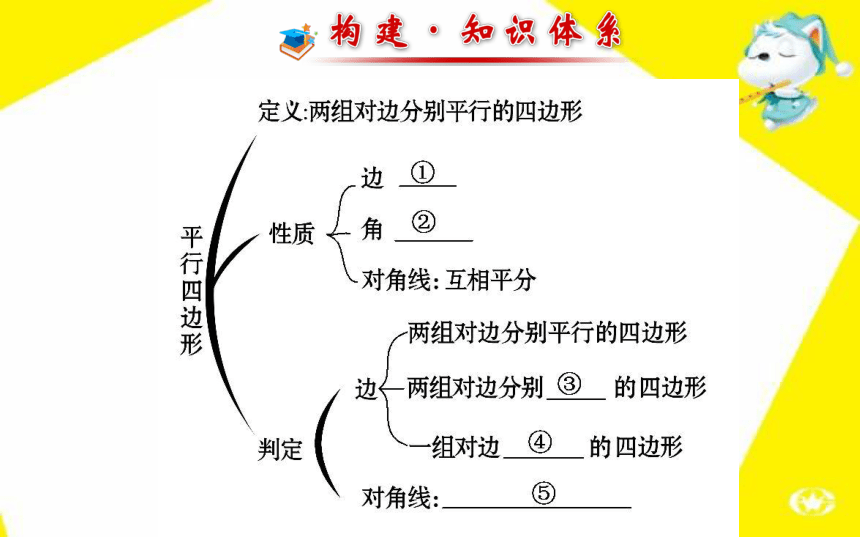
第 18 章请写出框图中数字处的内容:
①_______________;②___________________;
③_____;④___________;
⑤___________________________________.对边平行且相等对角相等,邻角互补相等平行且相等对角线互相平分的四边形是平行四边形考点 1 平行四边形的性质?
【知识点睛】
平行四边形边、角、对角线的性质
1.平行四边形的对边平行且相等.
2.平行四边形的对角相等,邻角互补.
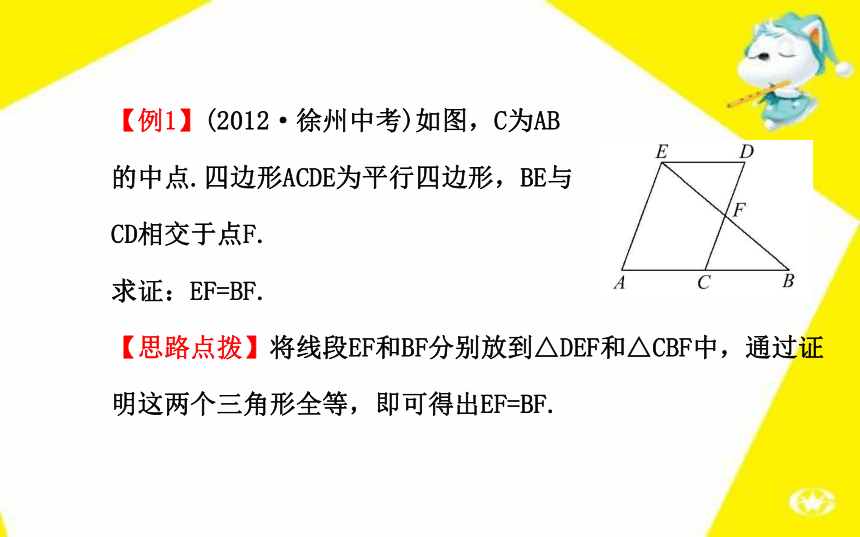
3.平行四边形的对角线互相平分.【例1】(2012·徐州中考)如图,C为AB
的中点.四边形ACDE为平行四边形,BE与
CD相交于点F.
求证:EF=BF.
【思路点拨】将线段EF和BF分别放到△DEF和△CBF中,通过证明这两个三角形全等,即可得出EF=BF.【自主解答】∵四边形ACDE为平行四边形,
∴ED=AC,ED∥AC.
∴∠D=∠FCB,∠DEF=∠B.
又∵C为AB的中点,∴AC=BC.∴ED=BC.
在△DEF和△CBF中,
∠D=∠FCB,ED=BC,∠DEF=∠B,
∴△DEF≌△CBF.∴EF=BF.【中考集训】
1.(2013·黔西南中考)已知□ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
【解析】选C.∵∠A+∠C=200°,∠A=∠C,∴∠A=100°.又∵AD∥BC,∴∠A+∠B=180°,∴∠B=80°.2.(2013·滨州中考)在□ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE= .
【解析】∵四边形ABCD是平行四边形,∴BO=DO.
又∵E是边CD的中点,∴OE是△DBC的中位线.
∵BC=10,∴OE= BC=5.
答案:53.(2012·成都中考)将□ABCD的一边BC延
长至E,若∠A=110°,则∠1= .
【解析】在□ABCD中,∠BCD=∠A=110°,∴∠1=180°-∠BCD=70°.
答案:70°4.(2012·广安中考)如图,四边形ABCD是平行四边形,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB.求证:△AEF≌△DFC.【证明】因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD.∵AB∥CD,∴∠EAF=∠D.
∵AF=AB,AB=CD,∴AF=CD.
∵BE=AD,AB=AF,∴AE=DF.
在△AEF和△DFC中,
∵AF=CD,∠EAF=∠D,AE=DF,
∴△AEF≌△DFC.考点 2 平行四边形的判定?
【知识点睛】 【例2】(2013·龙岩中考)如图,四边形ABCD是平行四边形,E,F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF.
(2)求证:四边形EBFD是平行四边形.【思路点拨】(1)先证△ADE与△CBF全等,再根据其性质得出结论.
(2)利用对边平行且相等的四边形是平行四边形证得结论;或利用对角线互相平分的四边形是平行四边形证得结论.【自主解答】(1)如图①:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4.
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2,
∴∠5=∠6,∴△ADE≌△CBF,∴AE =CF.(2)方法一:如图①,∵∠1=∠2,∴DE∥BF,
∵△ADE≌△CBF,∴DE=BF,
∴四边形EBFD是平行四边形.
方法二:如图②,连结BD.
∵AE=CF,∴OE=OF.又∵OB=OD,
∴四边形EBFD是平行四边形.【中考集训】
1.(2013·长春中考)如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连结AD,CD.若∠B=65°,则∠ADC的大小为 度.【解析】∵AD=BC,AB=CD,∴四边形ABCD是平行四边形,∴∠ADC=∠B=65°.
答案:652.(2013·南平中考)如图,在□ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
【证明】在□ABCD中,AD=BC且AD∥BC,
∵BE=FD,∴AF=CE,∴四边形AECF是平行四边形.3.(2013·鞍山中考)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:(1)△AFD≌△CEB.
(2)四边形ABCD是平行四边形.【证明】(1)∵DF∥BE,∴∠DFE=∠BEF.
又∵AF=CE,DF=BE,∴△AFD≌△CEB.
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,∴AD∥BC.
∴四边形ABCD是平行四边形.4.(2012·泰州中考)如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.【证明】∵AD∥BC,∴∠ADB=∠CBD.
∵AE⊥AD,CF⊥BC,∴∠EAD=∠FCB=90°.
又∵AE=CF,∴△ADE≌△CBF,∴AD=BC.
又∵AD∥BC,∴四边形ABCD是平行四边形.
第 18 章请写出框图中数字处的内容:
①_______________;②___________________;
③_____;④___________;
⑤___________________________________.对边平行且相等对角相等,邻角互补相等平行且相等对角线互相平分的四边形是平行四边形考点 1 平行四边形的性质?
【知识点睛】
平行四边形边、角、对角线的性质
1.平行四边形的对边平行且相等.
2.平行四边形的对角相等,邻角互补.
3.平行四边形的对角线互相平分.【例1】(2012·徐州中考)如图,C为AB
的中点.四边形ACDE为平行四边形,BE与
CD相交于点F.
求证:EF=BF.
【思路点拨】将线段EF和BF分别放到△DEF和△CBF中,通过证明这两个三角形全等,即可得出EF=BF.【自主解答】∵四边形ACDE为平行四边形,
∴ED=AC,ED∥AC.
∴∠D=∠FCB,∠DEF=∠B.
又∵C为AB的中点,∴AC=BC.∴ED=BC.
在△DEF和△CBF中,
∠D=∠FCB,ED=BC,∠DEF=∠B,
∴△DEF≌△CBF.∴EF=BF.【中考集训】
1.(2013·黔西南中考)已知□ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
【解析】选C.∵∠A+∠C=200°,∠A=∠C,∴∠A=100°.又∵AD∥BC,∴∠A+∠B=180°,∴∠B=80°.2.(2013·滨州中考)在□ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE= .
【解析】∵四边形ABCD是平行四边形,∴BO=DO.
又∵E是边CD的中点,∴OE是△DBC的中位线.
∵BC=10,∴OE= BC=5.
答案:53.(2012·成都中考)将□ABCD的一边BC延
长至E,若∠A=110°,则∠1= .
【解析】在□ABCD中,∠BCD=∠A=110°,∴∠1=180°-∠BCD=70°.
答案:70°4.(2012·广安中考)如图,四边形ABCD是平行四边形,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB.求证:△AEF≌△DFC.【证明】因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD.∵AB∥CD,∴∠EAF=∠D.
∵AF=AB,AB=CD,∴AF=CD.
∵BE=AD,AB=AF,∴AE=DF.
在△AEF和△DFC中,
∵AF=CD,∠EAF=∠D,AE=DF,
∴△AEF≌△DFC.考点 2 平行四边形的判定?
【知识点睛】 【例2】(2013·龙岩中考)如图,四边形ABCD是平行四边形,E,F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF.
(2)求证:四边形EBFD是平行四边形.【思路点拨】(1)先证△ADE与△CBF全等,再根据其性质得出结论.
(2)利用对边平行且相等的四边形是平行四边形证得结论;或利用对角线互相平分的四边形是平行四边形证得结论.【自主解答】(1)如图①:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4.
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2,
∴∠5=∠6,∴△ADE≌△CBF,∴AE =CF.(2)方法一:如图①,∵∠1=∠2,∴DE∥BF,
∵△ADE≌△CBF,∴DE=BF,
∴四边形EBFD是平行四边形.
方法二:如图②,连结BD.
∵AE=CF,∴OE=OF.又∵OB=OD,
∴四边形EBFD是平行四边形.【中考集训】
1.(2013·长春中考)如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连结AD,CD.若∠B=65°,则∠ADC的大小为 度.【解析】∵AD=BC,AB=CD,∴四边形ABCD是平行四边形,∴∠ADC=∠B=65°.
答案:652.(2013·南平中考)如图,在□ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
【证明】在□ABCD中,AD=BC且AD∥BC,
∵BE=FD,∴AF=CE,∴四边形AECF是平行四边形.3.(2013·鞍山中考)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:(1)△AFD≌△CEB.
(2)四边形ABCD是平行四边形.【证明】(1)∵DF∥BE,∴∠DFE=∠BEF.
又∵AF=CE,DF=BE,∴△AFD≌△CEB.
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,∴AD∥BC.
∴四边形ABCD是平行四边形.4.(2012·泰州中考)如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.【证明】∵AD∥BC,∴∠ADB=∠CBD.
∵AE⊥AD,CF⊥BC,∴∠EAD=∠FCB=90°.
又∵AE=CF,∴△ADE≌△CBF,∴AD=BC.
又∵AD∥BC,∴四边形ABCD是平行四边形.
