第10章相交线、平行线与平移单元培优测试卷
文档属性
| 名称 | 第10章相交线、平行线与平移单元培优测试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 121.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-04 00:00:00 | ||
图片预览


文档简介
第10章 相交线、平行线与平移
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.如图,三条直线AB、CD、EF相交于点O,则∠AOE+∠DOB+∠COF=…………【 】
A.120° B.150° C.180° D.200°
2.如图,AC⊥BC于点C,CD⊥AB于点D,能表示点到直线(或线段)的距离的线段有………………………………………………………………………………………【 】
A.2条 B.3条 C.4条 D.5条
3.如图,在∠1、∠2、∠3、∠4、∠5、∠6中,是同旁内角的有………………………【 】
A.6对 B.5对 C.4对 D.3对
4.如图,下列条件,能说明AB∥CD的有……………………………………………【 】
①∠1=∠D; ②∠EFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
5.如图,AB∥CD,OE平分∠AOD,OF⊥OE,∠D=56°,则∠BOF的度数为……【 】
A.28° B.29° C.30° D.34°
6.下列属于平移现象的有………………………………………………………………【 】
①滑雪运动员在雪地上沿直线滑行;②电梯上上下下迎送乘客;③健身时做转呼啦圈运动;④火车在笔直的铁轨上行驶.2·1·c·n·j·y
A.①② B.①②③ C. ①②④ D. ②③④
7.下列说法正确的是……………………………………………………………………【 】
A.a、b、c是直线,a∥b,b∥c,则a∥c B. a、b、c是直线,a⊥b,b⊥c,则a⊥c
C. a、b、c是直线,a∥b,b⊥c,则a∥c D. a、b、c是直线,a∥b,b∥c,则a⊥c
8.如图,将一条等宽的纸带,按如图所示折叠,所得∠ABD=140°,则图中∠ACE的度数为……………………………………………………………………………………【 】
A.100° B.110° C.120° D.140°
9.下列说法正确的是……………………………………………………………………【 】
A.画出点A到直线l的距离 B.过直线AB上的点C作CD⊥AB,CE⊥AB C. 过点O作OA⊥直线l,垂足为O D. 过直线AB上一点E作EF⊥AB,垂足为E
10.平面上有互不重合的四条直线,它们的交点个数可能是…………………………【 】
A.1,3,5 B.3,5,6 C.0,1,3,5,6 D.0,1,3,4,5,6
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,直线AB、CD交于点O,若∠AOC=2x°,∠BOC=(x+y+9)°,∠BOD=(y+4)°,则∠AOD的度数为________.21·世纪*教育网
12.如图,能判断CE∥AB的条件有________________________.
13.如图,AB⊥EF,CD⊥EF,∠GBE=∠F=45°,则图中与∠FCD相等的角有________.
14.如图,是一个长方形推拉窗,窗高1.2m,则活动窗的通风面积y(m2)与活动窗拉开长度x(m)之间的关系式为_____________. 21世纪教育网版权所有
三、(本大题共两小题,每小题8分,满分16分)
15.如图,直线AB、CD相交于点O,OE平分∠AOD,∠AOC与∠BOD的和为240°,求∠AOE与∠BOC的度数. 21教育网
16.如图,某化工厂M旁有一条河流,在河岸l的什么地方建一个水泵站供化工厂使用,才能使铺设的水管最短?请说明理由. www-2-1-cnjy-com
四、(本大题共两小题,每小题8分,满分16分)
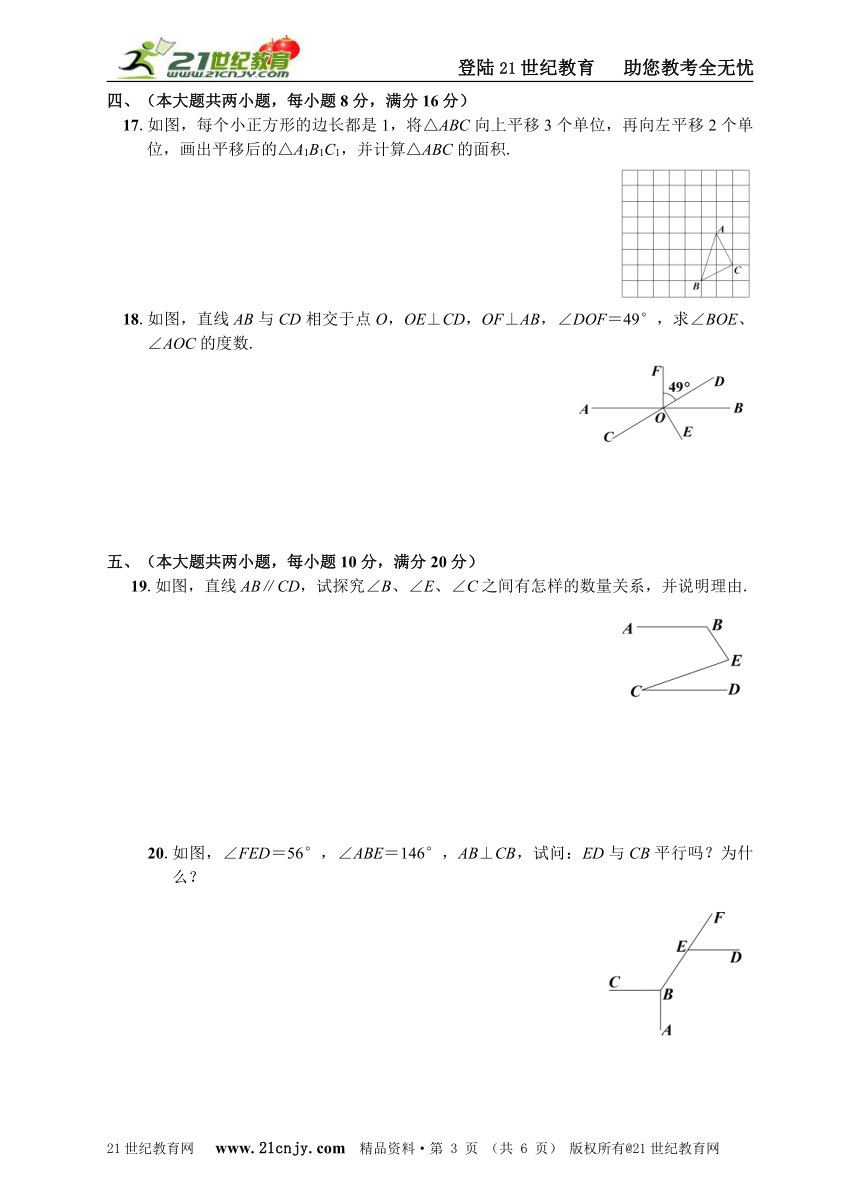
17.如图,每个小正方形的边长都是1,将△ABC向上平移3个单位,再向左平移2个单位,画出平移后的△A1B1C1,并计算△ABC的面积.2-1-c-n-j-y
18.如图,直线AB与CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=49°,求∠BOE、∠AOC的度数. 21*cnjy*com
五、(本大题共两小题,每小题10分,满分20分)
19.如图,直线AB∥CD,试探究∠B、∠E、∠C之间有怎样的数量关系,并说明理由.
20.如图,∠FED=56°,∠ABE=146°,AB⊥CB,试问:ED与CB平行吗?为什么?
六、(本题满分12分)
21.如图,BD⊥AC,于点D,且∠AGD=∠ABC,∠GDB=∠CEF,请问EF与AC垂直吗?为什么? 【来源:21·世纪·教育·网】
七、(本题满分12分)
22.如图,∠E=∠F,AB∥CD,请问∠A与∠C相等吗?请说明理由.
八、(本题满分14分)
23.在一次数学活动课上,方老师给同学们提出了一个问题:如果一个角的两边与另一个角的两边分别平行,那么这两个角之间是什么关系呢?21cnjy.com
小华的看法是:这两个角相等,如图1所示,∠1=∠2;
小明的看法是:这两个角互补,如图2所示,∠3+∠4=180°.
(1)你的看法是什么?请利用图1与图2说明你的理由.
(2)聪明的小徐又提出了一个新的问题:若这两个角的两边分别互相垂直,这两个角之间又是什么关系呢?请直接写出你猜想的结论.21·cn·jy·com
答案
1.C 2.D 3.B 4. C 5. A 6.C 7.A 8. B 9.D 10.D
11.110° 12.∠DCE=∠A,∠ECB=∠B,∠ECA+∠A=180° 13. ∠F,∠A,∠ABG,∠GBE 14.1.2x www.21-cn-jy.com
15.解:∵∠AOC=∠BOD,∠AOC+∠BOD=240°,
∴∠AOC=∠BOD=120°,
∴∠BOC=∠AOD=180°-120°=60°,
又∵OE平分∠AOD,
∴∠AOE=∠AOD=30°.
17.解:如下图;△ABC的面积为2×3-×1×3-×1×2-×1×2=2.5.
18.解:∵AB⊥OF,CD⊥OE,
∴∠BOF=∠DOE=90°,
∴∠BOD=90°-49°=41°,
∴∠AOC=∠BOD=41°,∠BOE=90°-∠BOD=90°-41°=49°.
19.解:∠B+∠E-∠C=180°,
理由如下:如下图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B+∠BEF=180°,∠FEC=∠C,
又∵∠BEC=∠BEF+∠FEC,
∴∠B+∠BEC-∠C=∠B+∠BEF+∠FEC-∠C=∠B+∠BEF=180°.
20.解:ED∥CB,
理由如下:∵AB⊥CB,
∴∠ABC=90°,
又∵∠ABE=146°,∠ABC+∠ABE+∠CBE=360°,
∴∠CBE=360°-90°-146°=124°.
∵∠FED=56°,∠FED+∠DEB=180°,
∴∠DEB=180°-56°=124°,
∴∠CBE=∠DEB,
∴ED∥CB.
∴EF∥BD,
∴∠EFC=∠BDC,
又∵BD⊥AC,
∴∠BDC=90°,
∴∠EFC=90°,
∴EF⊥AC.
22. ∠A=∠C,理由如下:∵∠E=∠F,
∴AE∥FC,
∴∠A=∠ABF,
又∵AB∥CD,
∴∠ABF=∠C,
∴∠A=∠C.
23.解:(1)这两个角之间的关系是相等或互补,
理由如下:如图1,∵AB∥ED,
∴∠1=∠5,
又∵BC∥EF,
∴∠2=∠5,
∴∠1=∠2;
如图2,∵AB∥ED,
∴∠3=∠6,
又∵BC∥EF,
∴∠4+∠6=180°,
∴∠3+∠4=180°,即∠3与∠4互补.
(满分:150分 时间:120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.如图,三条直线AB、CD、EF相交于点O,则∠AOE+∠DOB+∠COF=…………【 】
A.120° B.150° C.180° D.200°
2.如图,AC⊥BC于点C,CD⊥AB于点D,能表示点到直线(或线段)的距离的线段有………………………………………………………………………………………【 】
A.2条 B.3条 C.4条 D.5条
3.如图,在∠1、∠2、∠3、∠4、∠5、∠6中,是同旁内角的有………………………【 】
A.6对 B.5对 C.4对 D.3对
4.如图,下列条件,能说明AB∥CD的有……………………………………………【 】
①∠1=∠D; ②∠EFB+∠D=180°; ③∠B=∠D; ④∠BFD=∠D.
A.1个 B.2个 C.3个 D.4个
5.如图,AB∥CD,OE平分∠AOD,OF⊥OE,∠D=56°,则∠BOF的度数为……【 】
A.28° B.29° C.30° D.34°
6.下列属于平移现象的有………………………………………………………………【 】
①滑雪运动员在雪地上沿直线滑行;②电梯上上下下迎送乘客;③健身时做转呼啦圈运动;④火车在笔直的铁轨上行驶.2·1·c·n·j·y
A.①② B.①②③ C. ①②④ D. ②③④
7.下列说法正确的是……………………………………………………………………【 】
A.a、b、c是直线,a∥b,b∥c,则a∥c B. a、b、c是直线,a⊥b,b⊥c,则a⊥c
C. a、b、c是直线,a∥b,b⊥c,则a∥c D. a、b、c是直线,a∥b,b∥c,则a⊥c
8.如图,将一条等宽的纸带,按如图所示折叠,所得∠ABD=140°,则图中∠ACE的度数为……………………………………………………………………………………【 】
A.100° B.110° C.120° D.140°
9.下列说法正确的是……………………………………………………………………【 】
A.画出点A到直线l的距离 B.过直线AB上的点C作CD⊥AB,CE⊥AB C. 过点O作OA⊥直线l,垂足为O D. 过直线AB上一点E作EF⊥AB,垂足为E
10.平面上有互不重合的四条直线,它们的交点个数可能是…………………………【 】
A.1,3,5 B.3,5,6 C.0,1,3,5,6 D.0,1,3,4,5,6
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,直线AB、CD交于点O,若∠AOC=2x°,∠BOC=(x+y+9)°,∠BOD=(y+4)°,则∠AOD的度数为________.21·世纪*教育网
12.如图,能判断CE∥AB的条件有________________________.
13.如图,AB⊥EF,CD⊥EF,∠GBE=∠F=45°,则图中与∠FCD相等的角有________.
14.如图,是一个长方形推拉窗,窗高1.2m,则活动窗的通风面积y(m2)与活动窗拉开长度x(m)之间的关系式为_____________. 21世纪教育网版权所有
三、(本大题共两小题,每小题8分,满分16分)
15.如图,直线AB、CD相交于点O,OE平分∠AOD,∠AOC与∠BOD的和为240°,求∠AOE与∠BOC的度数. 21教育网
16.如图,某化工厂M旁有一条河流,在河岸l的什么地方建一个水泵站供化工厂使用,才能使铺设的水管最短?请说明理由. www-2-1-cnjy-com
四、(本大题共两小题,每小题8分,满分16分)
17.如图,每个小正方形的边长都是1,将△ABC向上平移3个单位,再向左平移2个单位,画出平移后的△A1B1C1,并计算△ABC的面积.2-1-c-n-j-y
18.如图,直线AB与CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=49°,求∠BOE、∠AOC的度数. 21*cnjy*com
五、(本大题共两小题,每小题10分,满分20分)
19.如图,直线AB∥CD,试探究∠B、∠E、∠C之间有怎样的数量关系,并说明理由.
20.如图,∠FED=56°,∠ABE=146°,AB⊥CB,试问:ED与CB平行吗?为什么?
六、(本题满分12分)
21.如图,BD⊥AC,于点D,且∠AGD=∠ABC,∠GDB=∠CEF,请问EF与AC垂直吗?为什么? 【来源:21·世纪·教育·网】
七、(本题满分12分)
22.如图,∠E=∠F,AB∥CD,请问∠A与∠C相等吗?请说明理由.
八、(本题满分14分)
23.在一次数学活动课上,方老师给同学们提出了一个问题:如果一个角的两边与另一个角的两边分别平行,那么这两个角之间是什么关系呢?21cnjy.com
小华的看法是:这两个角相等,如图1所示,∠1=∠2;
小明的看法是:这两个角互补,如图2所示,∠3+∠4=180°.
(1)你的看法是什么?请利用图1与图2说明你的理由.
(2)聪明的小徐又提出了一个新的问题:若这两个角的两边分别互相垂直,这两个角之间又是什么关系呢?请直接写出你猜想的结论.21·cn·jy·com
答案
1.C 2.D 3.B 4. C 5. A 6.C 7.A 8. B 9.D 10.D
11.110° 12.∠DCE=∠A,∠ECB=∠B,∠ECA+∠A=180° 13. ∠F,∠A,∠ABG,∠GBE 14.1.2x www.21-cn-jy.com
15.解:∵∠AOC=∠BOD,∠AOC+∠BOD=240°,
∴∠AOC=∠BOD=120°,
∴∠BOC=∠AOD=180°-120°=60°,
又∵OE平分∠AOD,
∴∠AOE=∠AOD=30°.
17.解:如下图;△ABC的面积为2×3-×1×3-×1×2-×1×2=2.5.
18.解:∵AB⊥OF,CD⊥OE,
∴∠BOF=∠DOE=90°,
∴∠BOD=90°-49°=41°,
∴∠AOC=∠BOD=41°,∠BOE=90°-∠BOD=90°-41°=49°.
19.解:∠B+∠E-∠C=180°,
理由如下:如下图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B+∠BEF=180°,∠FEC=∠C,
又∵∠BEC=∠BEF+∠FEC,
∴∠B+∠BEC-∠C=∠B+∠BEF+∠FEC-∠C=∠B+∠BEF=180°.
20.解:ED∥CB,
理由如下:∵AB⊥CB,
∴∠ABC=90°,
又∵∠ABE=146°,∠ABC+∠ABE+∠CBE=360°,
∴∠CBE=360°-90°-146°=124°.
∵∠FED=56°,∠FED+∠DEB=180°,
∴∠DEB=180°-56°=124°,
∴∠CBE=∠DEB,
∴ED∥CB.
∴EF∥BD,
∴∠EFC=∠BDC,
又∵BD⊥AC,
∴∠BDC=90°,
∴∠EFC=90°,
∴EF⊥AC.
22. ∠A=∠C,理由如下:∵∠E=∠F,
∴AE∥FC,
∴∠A=∠ABF,
又∵AB∥CD,
∴∠ABF=∠C,
∴∠A=∠C.
23.解:(1)这两个角之间的关系是相等或互补,
理由如下:如图1,∵AB∥ED,
∴∠1=∠5,
又∵BC∥EF,
∴∠2=∠5,
∴∠1=∠2;
如图2,∵AB∥ED,
∴∠3=∠6,
又∵BC∥EF,
∴∠4+∠6=180°,
∴∠3+∠4=180°,即∠3与∠4互补.
