图形的相似 （中位线）

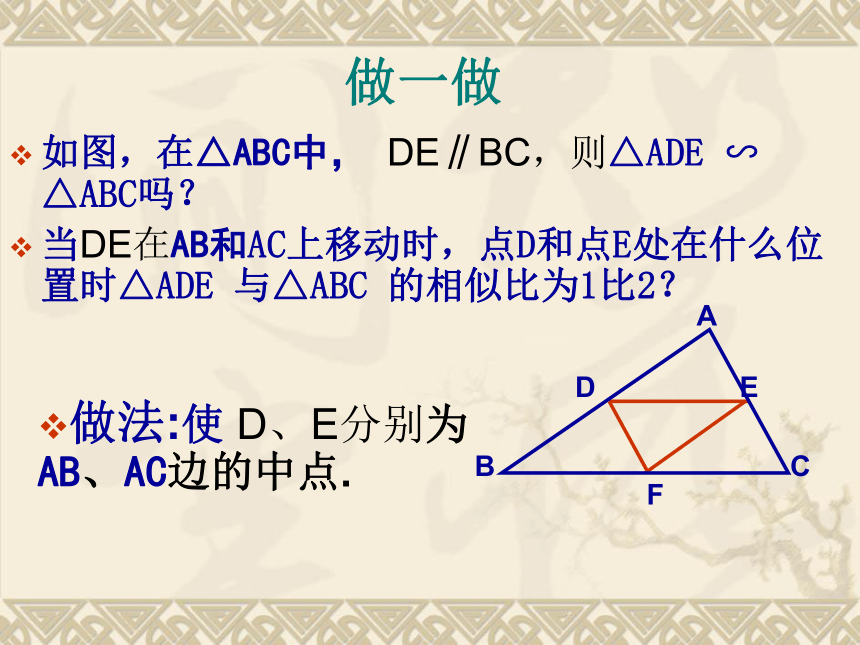
课件14张PPT。三角形的中位线学习目标1、认识三角形的中位线，会画三角形的中位线；2、理解三角形的中位线性质，会用中位线性质去解决相关问题；如图，在△ABC中， DE∥BC，则△ADE ∽ △ABC吗？
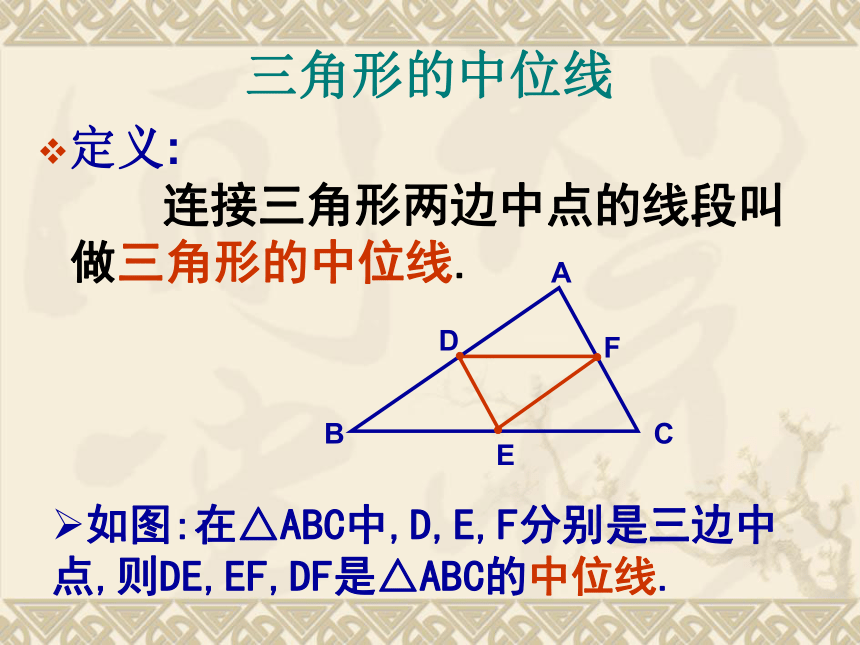
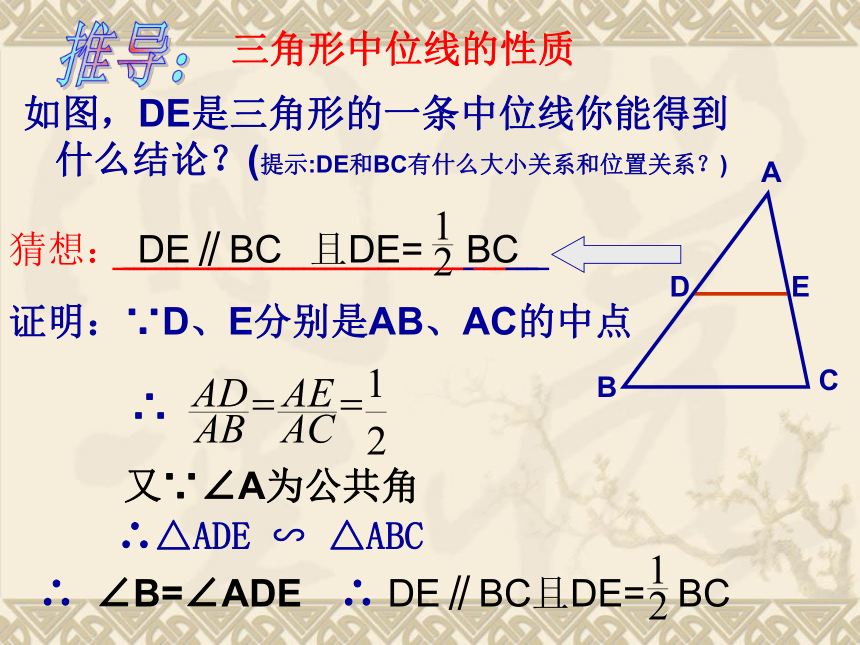
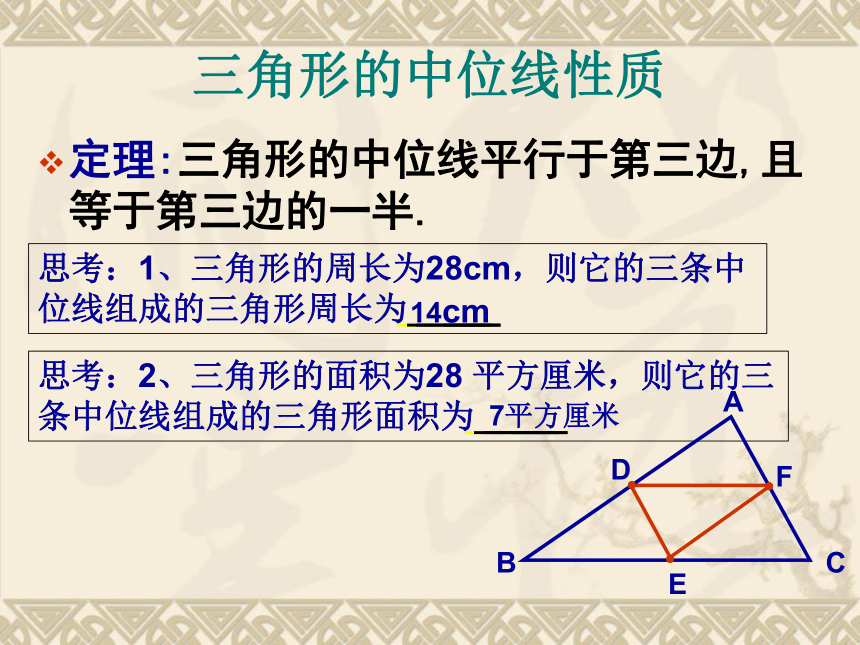
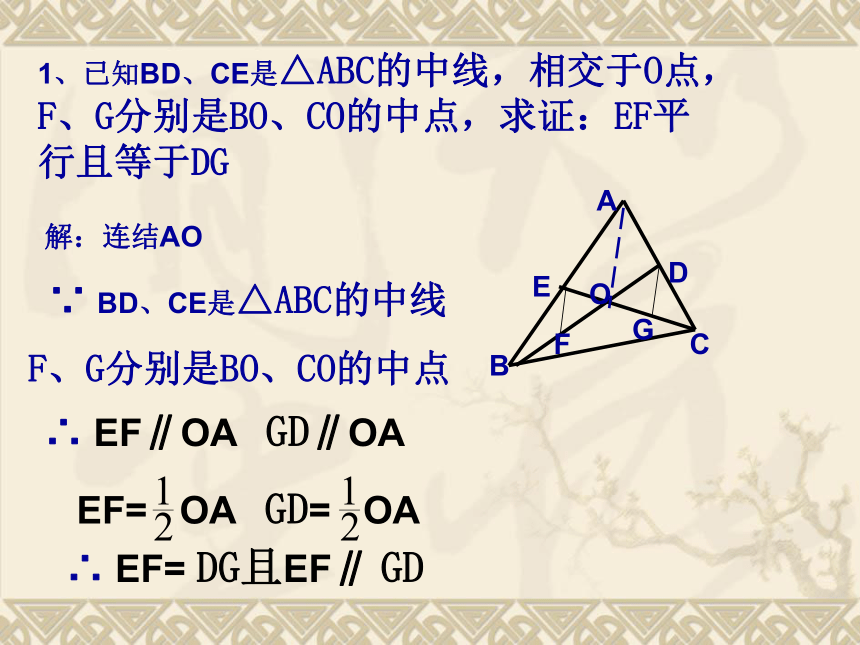
当DE在AB和AC上移动时，点D和点E处在什么位置时△ADE 与△ABC 的相似比为1比2？做一做做法:使 D、E分别为AB、AC边的中点.ABCDEF三角形的中位线定义: 连接三角形两边中点的线段叫做三角形的中位线.如图:在△ABC中,D,E,F分别是三边中点,则DE,EF,DF是△ABC的中位线.三角形中位线的性质如图，DE是三角形的一条中位线你能得到什么结论？(提示:DE和BC有什么大小关系和位置关系？)猜想：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?DE∥BC 且DE= BC推导：证明：∵D、E分别是AB、AC的中点∴又∵∠A为公共角∴△ADE ∽ △ABC ∴ ∠B=∠ADE∴ DE∥BC且DE= BC三角形的中位线性质定理:三角形的中位线平行于第三边,且等于第三边的一半.思考：1、三角形的周长为28cm，则它的三条中位线组成的三角形周长为? ? ? ? ? ?? ? ?? ? ?? 思考：2、三角形的面积为28 平方厘米，则它的三条中位线组成的三角形面积为? ? ? ? ? ?? ? ?? ? ?? 14cm7平方厘米1、已知BD、CE是△ABC的中线，相交于O点，F、G分别是BO、CO的中点，求证：EF平行且等于DG
ABCEDFOG ∵ BD、CE是△ABC的中线
F、G分别是BO、CO的中点
∴ EF∥OA GD∥OA
EF= OA GD= OA∴ EF= DG且EF∥ GD解：连结AO做一做如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新四边形的形状有什么特征?FG∥BD且FG= BD 四边形EFGH是平行四边形∴ EH∥FG且EH= FG∴四边形EHGF是平形四边形解:∵ EH∥BD且EH= BD
连结BD思考1、平行四边形各边中点围成的四边形是? ? ? ? ? ? ?? ? ?? ? ??
2、矩形各边中点围成的四边形是? ? ? ? ? ? ?? ? ?? ? ?? ? ?
3、菱形各边中点围成的四边形是? ? ? ? ? ? ?? ? ?? ? ?? ? ?
4、正方形各边中点围成的四边形是? ? ? ? ? ? ?? ? ?? ? ?? ? ?
5、等腰梯形各边中点围成的四边形是? ? ? ? ? ? ?? ? ?? ? ?? ? ?平行四边形
菱形菱形矩形正方形6、任意四边形各边中点围成的四边形是平行四边形
2、求证三角形的一条中位线与第三边的中线互相平分典型例题：ABCDFE已知：如图所示，在△ABC中AD=DB，AF=FC，BE=EC 求证：AE、DF互相平分 证明：连结DE、EF∵ D、E、F分别为AB、BC、AC上中点∴DE、EF为△ABC的中位线DE ∥ AF、AD ∥EF四边形ADEF是 ∴AE、DF互相平分如图所示， △ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G，求证：BDGACE思考题：小结三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线性质:三角形的中位线平行于第三边,且等于第三边的一半.任意四边形四边中点连线所组成的四边形是：平行四边行
作业 课 本 练习第1题、习题3、4题；再见！