2023-2024学年贵州省遵义市仁怀市七年级(上)期末数学模拟试卷(含解析)
文档属性
| 名称 | 2023-2024学年贵州省遵义市仁怀市七年级(上)期末数学模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-07 22:36:26 | ||
图片预览




文档简介
2023-2024学年贵州省遵义市仁怀市七年级(上)期末数学模拟试卷
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)中国人最早使用负数,可追溯到两千多年前的秦汉时期,2021的相反数是( )
A.2021 B.﹣2021 C. D.
2.(3分)某地区2021年元旦的最高气温为9℃,最低气温为﹣3℃,那么该地区这天的最低气温比最高气温低( )
A.6℃ B.﹣6℃ C.12℃ D.﹣12℃
3.(3分)据2021年3月17日《天津日报》报道,今年我市冬小麦播种面积增加到1510000亩,比去年增加200000亩,确保全年粮食种植面积和总产量双增长.将1510000用科学记数法表示应为( )
A.0.151×107 B.1.51×106 C.15.1×105 D.151×104
4.(3分)在算式____+6=﹣8中,括号里应填( )
A.2 B.﹣2 C.14 D.﹣14
5.(3分)有理数a、b在数轴上的位置如图所示,则下列各式:①a+b>0;②a﹣b>0;③|b|>a;④ab<0;⑤|a﹣b|=a﹣b,正确的有( )
A.1个 B.2个 C.3个 D.4个
6.(3分)已知a=b,下列变形错误的是( )
A.a+3=b+3 B.ab C. D.2a﹣1=1﹣2b
7.(3分)我市在创建“全国文明城市”时,小明特制了一个正方体模具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字是( )
A.全 B.国 C.明 D.城
8.(3分)如图是某同学用黑白两种颜色的正方形纸片,按照一定规律拼成的一列图案,按照此规律,第200个图案中白色纸片的张数为( )
A.600 B.601张 C.800张 D.801张
9.(3分)一个三位数的个位数字是a,十位数字是0,百位数字是b,则这个三位数可表示为( )
A.ab B.a+b C.100a+b D.100b+a
10.(3分)质检员抽查4个方便面,其中超过标准成量的克数记为正数,不足标准量的克数记为负数,从质量的角度看,最接近标准的产品是( )
A.+1.5 B.+0.6 C.﹣2.5 D.﹣0.5
11.(3分)若小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东60°方向行走至点C处,则∠ABC等于( )
A.20° B.100° C.110° D.130°
12.(3分)小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为69千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈同坐在跷跷板的一端,这时爸爸的一端仍然着地.后来小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地.小宝体重可能是( )
A.23.3千克 B.23千克 C.21.1千克 D.19.9千克
二.填空题(共4小题,满分16分,每小题4分)
13.(4分)比较大小: ;﹣3 ﹣4.
14.(4分)探究规律:
(1)计算:
①2﹣1= ;②22﹣2﹣1= ;③23﹣22﹣2﹣1= ;④24﹣23﹣22﹣2﹣1= .
(2)根据上面计算结果猜想:①22019﹣22018﹣22017﹣…﹣22﹣2﹣1= ;
②212﹣211﹣210﹣29﹣28﹣27﹣26= .
15.(4分)若某数除以4再减去2,等于这个数的加上8,则这个数为 .
16.(4分)如图,将一张矩形纸对折两次,然后剪下一个角,打开.怎样剪才能剪出一个正方形?
答:只要保证剪口线与折痕的角度为 即可.因为正方形的两条对角线把它分成四个全等的 三角形,把折痕作对角线,这时只需剪一个等腰直角三角形打开即是正方形.
三.解答题(共9小题,满分98分)
17.(8分)计算:
(1);
(2)(﹣20)+(+3)﹣(﹣5)﹣(+7);
(3);
(4);
(5)2×(﹣3)3﹣4×(﹣3)+15;
(6)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2).
18.(10分)解方程:3﹣6(x).
19.(10分)已知A=2x2+xy+3y,B=x2﹣xy.若(x+2)2+|y﹣3|=0,求A+B的值.
20.(10分)尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.(1)在直线l上求一点Q,使到A、B两点距离之和最短;(2)在直线l上求一点P,使PA=PB.
21.(10分)如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),D→ (﹣4,﹣2);
(2)若这只甲虫从A处去P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫从B处去Q处的行走路线依次为(a1,b1)(a2,b2)(a3,b3),…,(an,bn),则a1﹣b1+a2﹣b2+a3﹣b3+…+an﹣bn= .
22.(12分)探索规律:将连续的偶2,4,6,8,…,排成如图:
(1)请你求出十字框中的五个数的和;
(2)设中间的数为x,请你用含x的式子表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,这五个数的和能等于2018吗?如能,写出这五个数,如不能,请说明理由.
23.(12分)已知:有理数m所表示的点到原点距离4个单位,a、b互为相反数、且都不为零,c,d互为倒数.
(1)求m的值;
(2)求:2(a+b)﹣3cd+m的值.
24.(12分)某县在创建省级卫生文明县城中,对县城内的河道进行整治.现有一段长为180米的河道整治任务由甲、乙两个工程队先后接力完成.甲工程队每天整治8米,乙工程队每天整治12米,共用时20天.
(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意,得.
小华同学:设整治任务完成后,m表示 ,n表示 ;
得.
请你补全小明、小华两位同学的解题思路.
(2)求甲、乙两工程队分别整治河道多少米?请从中任选一个解题思路写出完整的解答过程.
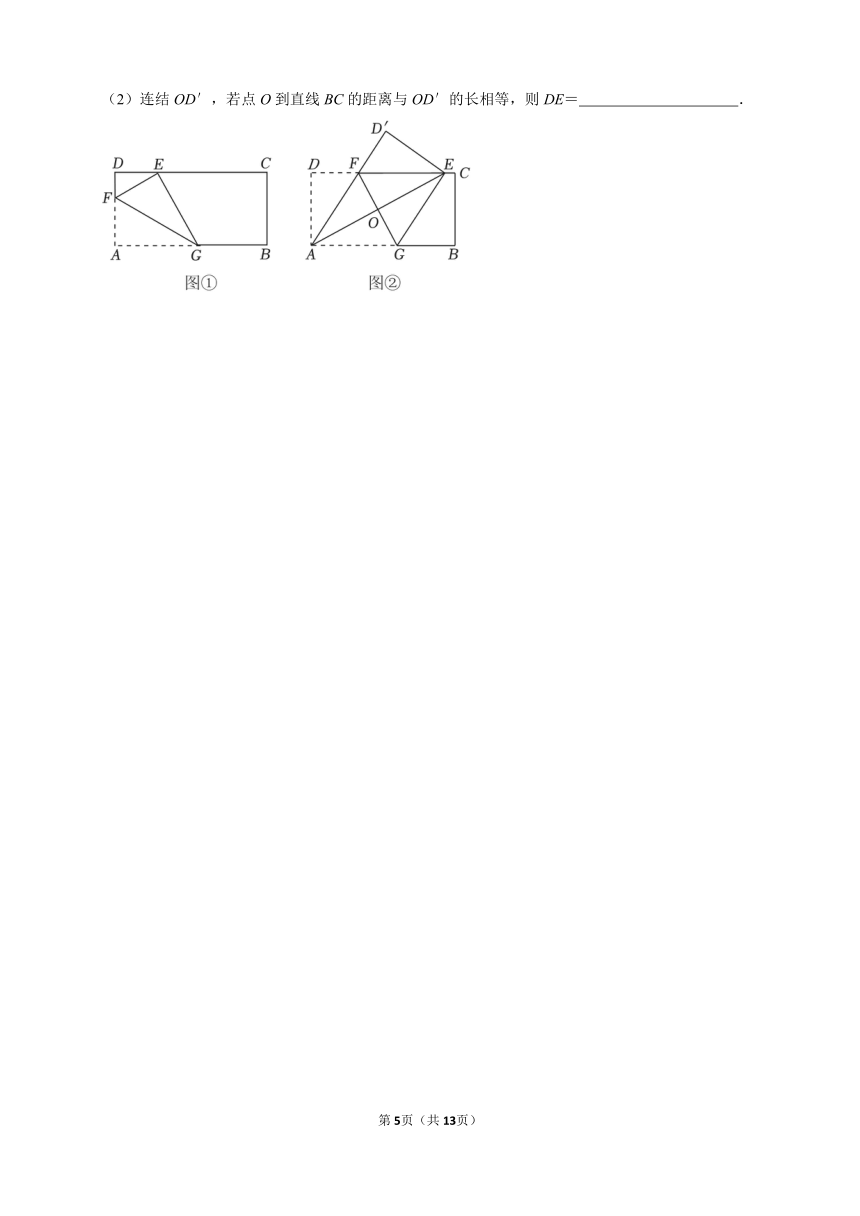
25.(14分)已知矩形纸片ABCD,AB=20,AD=10.将矩形纸片折叠,使点A落在CD边上,点A的对应点为点E,折痕为FG.
操作一:如图①,如果折痕FG分别与AD、AB交于点F、G,且,则DE= .
操作二:如图②,如果折痕FG分别与CD、AB交于点F、G,连结AE,AF,设AE交FG于点O,点D的对应点为点D′.
(1)判断四边形AGEF的形状,并说明理由;
(2)连结OD′,若点O到直线BC的距离与OD′的长相等,则DE= .
2023-2024学年贵州省遵义市仁怀市七年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.【解答】解:2021的相反数是:﹣2021.
故选:B.
2.【解答】解:9﹣(﹣3)
=9+3
=12(℃),
故选:C.
3.【解答】解:1510000=1.51×106.
故选:B.
4.【解答】解:﹣8﹣6=﹣14,
故选:D.
5.【解答】解:观察图象可知:a+b<0,a﹣b>0,|b|>a,ab<0,|a﹣b|=a﹣b,
②③④⑤正确,
故选:D.
6.【解答】解:∵a=b,
∴a+3=b+3,ab,,2a﹣1=2b﹣1,
故A、B、C正确,D错误.
故选:D.
7.【解答】解:∵正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,
∴在此正方体上与“文”字相对的面上的汉字是“城”.
故选:D.
8.【解答】解:由题目得,第1个图案中,白色纸片的个数为4+3×0;
第2个图案中,白色纸片的个数为4+3×1;
第3个图案中,白色纸片的个数为4+3×2;
…,
进一步发现规律:第n个图案中,白色纸片的个数为4+3(n﹣1)=3n+1,
当n=200时,图案中有白色纸片为3×200+1=601,
故选:B.
9.【解答】解:一个三位数的个位数字是a,十位数字是0,百位数字是b,
则这个三位数可表示为:100a+10×0+b=100a+b,
故选:D.
10.【解答】解:∵|﹣0.5|<|+0.6|<|+1.5|<|﹣2.5|,
∴﹣0.5最接近标准,
故选:D.
11.【解答】解:如图:
∵小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东60°方向行走至点C处,
∴∠DAB=40°,∠CBE=60°,
∵向北方向线是平行的,即AD∥BE,
∴∠ABE=∠DAB=40°,
∴∠ABC=∠ABE+∠EBC=40°+60°=100°.
故选:B.
12.【解答】解:设小宝的体重为x千克.
故,
所以23>x≥21,
故选:C.
二.填空题(共4小题,满分16分,每小题4分)
13.【解答】解:;
|﹣3|=3,|﹣4|=4,
∵3<4,
∴﹣3>﹣4.
故答案为:>,>.
14.【解答】解:(1)①2﹣1=1,
②22﹣2﹣1=1,
③23﹣22﹣2﹣1=1,
④24﹣23﹣22﹣2﹣1=1,
故答案为:①1;②1;③1;④1;
(2)由(1)可得:2n﹣2n﹣1﹣2n﹣2﹣…﹣22﹣2﹣1=1,
①22019﹣22018﹣22017﹣…﹣22﹣2﹣1=1,
故答案为:1;
②212﹣211﹣210﹣29﹣28﹣27﹣26
=212﹣211﹣210﹣29﹣28﹣27﹣26﹣…﹣22﹣2﹣1+(25+24+23+22+2+1)
=1+32+16+8+4+2+1
=64.
故答案为:64.
15.【解答】解:设这个数为x,根据题意得:,
解得x=﹣120.
故答案为:﹣120.
16.【解答】解:只要保证剪口线与折痕的角度为45°即可.因为正方形的两条对角线把它分成四个全等的等腰直角三角形,把折痕作对角线,这时只需剪一个等腰直角三角形打开即是正方形.
故答案为:45°,等腰直角.
三.解答题(共9小题,满分98分)
17.【解答】解:(1)原式
=9﹣11
=﹣2;
(2)原式=﹣20+3+5﹣7
=3+5﹣(20+7)
=8﹣27
=﹣19;
(3)原式
;
(4)原式
;
(5)原式=2×(﹣27)﹣(﹣12)+15
=﹣54+12+15
=﹣27;
(6)原式=﹣8+(﹣3)×18﹣9÷(﹣2)
=﹣8﹣54+4.5
=﹣57.5.
18.【解答】解:3﹣6(x),
则3﹣6x﹣4,
﹣6x,
解得:x.
19.【解答】解:∵(x+2)2+|y﹣3|=0,(x+2)2≥0,|y﹣3|≥0,
∴x+2=0,y﹣3=0.
∴x=﹣2,y=3.
A+B
=(2x2+xy+3y)+(x2﹣xy)
=2x2+xy+3y+x2﹣xy
=3x2+3y,
当x=﹣2,y=3时,
A+B
=3×(﹣2)2+3×3
=3×4+3×3
=12+9
=21.
20.【解答】解:(1)如图所示,点Q即为所求;
(2)如图所示,点P即为所求.
21.【解答】解:(1)规定:向上向右走为正,向下向左走为负,
∴A→C记为(3,4)B→C记为(2,0),D→A记为(﹣4,﹣2);
(2)P点位置如图所示.
(3)∵B→Q(+4,﹣3),
若这只甲虫从B处去Q处的行走路线依次为(a1,b1)(a2,b2)(a3,b3),…,(an,bn),则a1﹣b1+a2﹣b2+a3﹣b3+…+an﹣bn=(a1+a2+a3+…+an)﹣(b1+b2+b3+…+bn)=4﹣(﹣3)=7.
故答案为:(1)3;4;A;(3)7.
22.【解答】解:(1)十字框框出5个数的和为:6+14+16+18+26=80;
(2)根据题意得:
x上边的数字为:x﹣10,
x下边的数字为:x+10,
x左边的数字为:x﹣2,
x右边的数字为:x+2,
则十字框中的五个数字之和为:(x﹣10)+(x+10)+(x﹣2)+(x+2)+x=5x,
即用含x的代数式表示十字框框住的5个数字之和为5x;
(3)设中间的数为m,
根据题意得:5m=2018,
解得:m=403.6,
m不是整数,
即不能框住五个数,和等于2018.
23.【解答】解:(1)∵有理数m所表示的点到原点距离4个单位,
∴m=±4;
(2)∵理数m所表示的点到原点距离4个单位,a、b互为相反数、且都不为零,c,d互为倒数,
∴m=±4,a+b=0,cd=1,
∴当m=4时,2(a+b)﹣3cd+m
=2×0﹣3×1+4
=0﹣3+4
=1;
当m=﹣4时,2(a+b)﹣3cd+m
=2×0﹣3×1+(﹣4)
=0﹣3+(﹣4)
=﹣7;
即2(a+b)﹣3cd+m的值是1或﹣7.
24.【解答】解:(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意得;
小华同学:设整治任务完成后,m表示甲工程队整治河道用的天数,n表示乙工程队整治河道用时的天数;
得,
故答案为:甲工程队整治河道用的天数,乙工程队整治河道用时的天数;
(2)选小明同学所列方程组解答如下:
设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
由题意得:,
解得:,
答:甲工程队整治河道120米,乙工程队整治河道60米.
25.【解答】解:操作一,∵四边形ABCD为矩形,
∴∠A=∠D=90°.
∵将矩形纸片折叠,使点A落在CD边上,点A的对应点为点E,折痕为FG,
∴△AFG≌△EFG,
∴AF=EF,
∵AD=10,
∴DF=AD﹣AF.
在Rt△DEF中,
∵DF2+DE2=EF2,
∴DE.
故答案为:;
操作二:①四边形AGEF的形状是菱形,理由:
∵FG为折痕,
∴点A与点E关于FG对称,
∴FG垂直平分AE,
∴FG⊥AE,AO=OE.
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠FEO=∠GAO.
在△EFO和△AGO中,
,
∴△EFO≌△AGO(ASA),
∴FO=GO,FE=GA.
∵FE∥GA,
∴四边形AGEF为平行四边形,
∵FG⊥AE,
∴四边形AGEF是菱形;
②连结OD′,过点O作OH⊥BC于点H,如图,
则OD′=OH.
∵四边形ABCD为矩形,
∴AB⊥BC,DC⊥BC,
∵OH⊥BC,
∴AB∥OH∥CD,
由①知:AO=OE,
∴OH为梯形ABCE的中位线,
∴EC+AB=2OH,
∴EC+AB=2OD′.
设DE=x,则EC=20﹣x,
∴AE.
由题意得:∠D=∠D′=90°,
∵AO=OE,
∴D′O为Rt△AD′E斜边上的中线,
∴D′OAE,
∴OH=OD′AE,
∴20+20﹣x=2,
∴x.
∴DE.
故答案为:.
第1页(共1页)
一.选择题(共12小题,满分36分,每小题3分)
1.(3分)中国人最早使用负数,可追溯到两千多年前的秦汉时期,2021的相反数是( )
A.2021 B.﹣2021 C. D.
2.(3分)某地区2021年元旦的最高气温为9℃,最低气温为﹣3℃,那么该地区这天的最低气温比最高气温低( )
A.6℃ B.﹣6℃ C.12℃ D.﹣12℃
3.(3分)据2021年3月17日《天津日报》报道,今年我市冬小麦播种面积增加到1510000亩,比去年增加200000亩,确保全年粮食种植面积和总产量双增长.将1510000用科学记数法表示应为( )
A.0.151×107 B.1.51×106 C.15.1×105 D.151×104
4.(3分)在算式____+6=﹣8中,括号里应填( )
A.2 B.﹣2 C.14 D.﹣14
5.(3分)有理数a、b在数轴上的位置如图所示,则下列各式:①a+b>0;②a﹣b>0;③|b|>a;④ab<0;⑤|a﹣b|=a﹣b,正确的有( )
A.1个 B.2个 C.3个 D.4个
6.(3分)已知a=b,下列变形错误的是( )
A.a+3=b+3 B.ab C. D.2a﹣1=1﹣2b
7.(3分)我市在创建“全国文明城市”时,小明特制了一个正方体模具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字是( )
A.全 B.国 C.明 D.城
8.(3分)如图是某同学用黑白两种颜色的正方形纸片,按照一定规律拼成的一列图案,按照此规律,第200个图案中白色纸片的张数为( )
A.600 B.601张 C.800张 D.801张
9.(3分)一个三位数的个位数字是a,十位数字是0,百位数字是b,则这个三位数可表示为( )
A.ab B.a+b C.100a+b D.100b+a
10.(3分)质检员抽查4个方便面,其中超过标准成量的克数记为正数,不足标准量的克数记为负数,从质量的角度看,最接近标准的产品是( )
A.+1.5 B.+0.6 C.﹣2.5 D.﹣0.5
11.(3分)若小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东60°方向行走至点C处,则∠ABC等于( )
A.20° B.100° C.110° D.130°
12.(3分)小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为69千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈同坐在跷跷板的一端,这时爸爸的一端仍然着地.后来小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果爸爸被跷起离地.小宝体重可能是( )
A.23.3千克 B.23千克 C.21.1千克 D.19.9千克
二.填空题(共4小题,满分16分,每小题4分)
13.(4分)比较大小: ;﹣3 ﹣4.
14.(4分)探究规律:
(1)计算:
①2﹣1= ;②22﹣2﹣1= ;③23﹣22﹣2﹣1= ;④24﹣23﹣22﹣2﹣1= .
(2)根据上面计算结果猜想:①22019﹣22018﹣22017﹣…﹣22﹣2﹣1= ;
②212﹣211﹣210﹣29﹣28﹣27﹣26= .
15.(4分)若某数除以4再减去2,等于这个数的加上8,则这个数为 .
16.(4分)如图,将一张矩形纸对折两次,然后剪下一个角,打开.怎样剪才能剪出一个正方形?
答:只要保证剪口线与折痕的角度为 即可.因为正方形的两条对角线把它分成四个全等的 三角形,把折痕作对角线,这时只需剪一个等腰直角三角形打开即是正方形.
三.解答题(共9小题,满分98分)
17.(8分)计算:
(1);
(2)(﹣20)+(+3)﹣(﹣5)﹣(+7);
(3);
(4);
(5)2×(﹣3)3﹣4×(﹣3)+15;
(6)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2).
18.(10分)解方程:3﹣6(x).
19.(10分)已知A=2x2+xy+3y,B=x2﹣xy.若(x+2)2+|y﹣3|=0,求A+B的值.
20.(10分)尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.(1)在直线l上求一点Q,使到A、B两点距离之和最短;(2)在直线l上求一点P,使PA=PB.
21.(10分)如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),D→ (﹣4,﹣2);
(2)若这只甲虫从A处去P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫从B处去Q处的行走路线依次为(a1,b1)(a2,b2)(a3,b3),…,(an,bn),则a1﹣b1+a2﹣b2+a3﹣b3+…+an﹣bn= .
22.(12分)探索规律:将连续的偶2,4,6,8,…,排成如图:
(1)请你求出十字框中的五个数的和;
(2)设中间的数为x,请你用含x的式子表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,这五个数的和能等于2018吗?如能,写出这五个数,如不能,请说明理由.
23.(12分)已知:有理数m所表示的点到原点距离4个单位,a、b互为相反数、且都不为零,c,d互为倒数.
(1)求m的值;
(2)求:2(a+b)﹣3cd+m的值.
24.(12分)某县在创建省级卫生文明县城中,对县城内的河道进行整治.现有一段长为180米的河道整治任务由甲、乙两个工程队先后接力完成.甲工程队每天整治8米,乙工程队每天整治12米,共用时20天.
(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意,得.
小华同学:设整治任务完成后,m表示 ,n表示 ;
得.
请你补全小明、小华两位同学的解题思路.
(2)求甲、乙两工程队分别整治河道多少米?请从中任选一个解题思路写出完整的解答过程.
25.(14分)已知矩形纸片ABCD,AB=20,AD=10.将矩形纸片折叠,使点A落在CD边上,点A的对应点为点E,折痕为FG.
操作一:如图①,如果折痕FG分别与AD、AB交于点F、G,且,则DE= .
操作二:如图②,如果折痕FG分别与CD、AB交于点F、G,连结AE,AF,设AE交FG于点O,点D的对应点为点D′.
(1)判断四边形AGEF的形状,并说明理由;
(2)连结OD′,若点O到直线BC的距离与OD′的长相等,则DE= .
2023-2024学年贵州省遵义市仁怀市七年级(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.【解答】解:2021的相反数是:﹣2021.
故选:B.
2.【解答】解:9﹣(﹣3)
=9+3
=12(℃),
故选:C.
3.【解答】解:1510000=1.51×106.
故选:B.
4.【解答】解:﹣8﹣6=﹣14,
故选:D.
5.【解答】解:观察图象可知:a+b<0,a﹣b>0,|b|>a,ab<0,|a﹣b|=a﹣b,
②③④⑤正确,
故选:D.
6.【解答】解:∵a=b,
∴a+3=b+3,ab,,2a﹣1=2b﹣1,
故A、B、C正确,D错误.
故选:D.
7.【解答】解:∵正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,
∴在此正方体上与“文”字相对的面上的汉字是“城”.
故选:D.
8.【解答】解:由题目得,第1个图案中,白色纸片的个数为4+3×0;
第2个图案中,白色纸片的个数为4+3×1;
第3个图案中,白色纸片的个数为4+3×2;
…,
进一步发现规律:第n个图案中,白色纸片的个数为4+3(n﹣1)=3n+1,
当n=200时,图案中有白色纸片为3×200+1=601,
故选:B.
9.【解答】解:一个三位数的个位数字是a,十位数字是0,百位数字是b,
则这个三位数可表示为:100a+10×0+b=100a+b,
故选:D.
10.【解答】解:∵|﹣0.5|<|+0.6|<|+1.5|<|﹣2.5|,
∴﹣0.5最接近标准,
故选:D.
11.【解答】解:如图:
∵小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东60°方向行走至点C处,
∴∠DAB=40°,∠CBE=60°,
∵向北方向线是平行的,即AD∥BE,
∴∠ABE=∠DAB=40°,
∴∠ABC=∠ABE+∠EBC=40°+60°=100°.
故选:B.
12.【解答】解:设小宝的体重为x千克.
故,
所以23>x≥21,
故选:C.
二.填空题(共4小题,满分16分,每小题4分)
13.【解答】解:;
|﹣3|=3,|﹣4|=4,
∵3<4,
∴﹣3>﹣4.
故答案为:>,>.
14.【解答】解:(1)①2﹣1=1,
②22﹣2﹣1=1,
③23﹣22﹣2﹣1=1,
④24﹣23﹣22﹣2﹣1=1,
故答案为:①1;②1;③1;④1;
(2)由(1)可得:2n﹣2n﹣1﹣2n﹣2﹣…﹣22﹣2﹣1=1,
①22019﹣22018﹣22017﹣…﹣22﹣2﹣1=1,
故答案为:1;
②212﹣211﹣210﹣29﹣28﹣27﹣26
=212﹣211﹣210﹣29﹣28﹣27﹣26﹣…﹣22﹣2﹣1+(25+24+23+22+2+1)
=1+32+16+8+4+2+1
=64.
故答案为:64.
15.【解答】解:设这个数为x,根据题意得:,
解得x=﹣120.
故答案为:﹣120.
16.【解答】解:只要保证剪口线与折痕的角度为45°即可.因为正方形的两条对角线把它分成四个全等的等腰直角三角形,把折痕作对角线,这时只需剪一个等腰直角三角形打开即是正方形.
故答案为:45°,等腰直角.
三.解答题(共9小题,满分98分)
17.【解答】解:(1)原式
=9﹣11
=﹣2;
(2)原式=﹣20+3+5﹣7
=3+5﹣(20+7)
=8﹣27
=﹣19;
(3)原式
;
(4)原式
;
(5)原式=2×(﹣27)﹣(﹣12)+15
=﹣54+12+15
=﹣27;
(6)原式=﹣8+(﹣3)×18﹣9÷(﹣2)
=﹣8﹣54+4.5
=﹣57.5.
18.【解答】解:3﹣6(x),
则3﹣6x﹣4,
﹣6x,
解得:x.
19.【解答】解:∵(x+2)2+|y﹣3|=0,(x+2)2≥0,|y﹣3|≥0,
∴x+2=0,y﹣3=0.
∴x=﹣2,y=3.
A+B
=(2x2+xy+3y)+(x2﹣xy)
=2x2+xy+3y+x2﹣xy
=3x2+3y,
当x=﹣2,y=3时,
A+B
=3×(﹣2)2+3×3
=3×4+3×3
=12+9
=21.
20.【解答】解:(1)如图所示,点Q即为所求;
(2)如图所示,点P即为所求.
21.【解答】解:(1)规定:向上向右走为正,向下向左走为负,
∴A→C记为(3,4)B→C记为(2,0),D→A记为(﹣4,﹣2);
(2)P点位置如图所示.
(3)∵B→Q(+4,﹣3),
若这只甲虫从B处去Q处的行走路线依次为(a1,b1)(a2,b2)(a3,b3),…,(an,bn),则a1﹣b1+a2﹣b2+a3﹣b3+…+an﹣bn=(a1+a2+a3+…+an)﹣(b1+b2+b3+…+bn)=4﹣(﹣3)=7.
故答案为:(1)3;4;A;(3)7.
22.【解答】解:(1)十字框框出5个数的和为:6+14+16+18+26=80;
(2)根据题意得:
x上边的数字为:x﹣10,
x下边的数字为:x+10,
x左边的数字为:x﹣2,
x右边的数字为:x+2,
则十字框中的五个数字之和为:(x﹣10)+(x+10)+(x﹣2)+(x+2)+x=5x,
即用含x的代数式表示十字框框住的5个数字之和为5x;
(3)设中间的数为m,
根据题意得:5m=2018,
解得:m=403.6,
m不是整数,
即不能框住五个数,和等于2018.
23.【解答】解:(1)∵有理数m所表示的点到原点距离4个单位,
∴m=±4;
(2)∵理数m所表示的点到原点距离4个单位,a、b互为相反数、且都不为零,c,d互为倒数,
∴m=±4,a+b=0,cd=1,
∴当m=4时,2(a+b)﹣3cd+m
=2×0﹣3×1+4
=0﹣3+4
=1;
当m=﹣4时,2(a+b)﹣3cd+m
=2×0﹣3×1+(﹣4)
=0﹣3+(﹣4)
=﹣7;
即2(a+b)﹣3cd+m的值是1或﹣7.
24.【解答】解:(1)小明、小华两位同学提出的解题思路如下:
小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
根据题意得;
小华同学:设整治任务完成后,m表示甲工程队整治河道用的天数,n表示乙工程队整治河道用时的天数;
得,
故答案为:甲工程队整治河道用的天数,乙工程队整治河道用时的天数;
(2)选小明同学所列方程组解答如下:
设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.
由题意得:,
解得:,
答:甲工程队整治河道120米,乙工程队整治河道60米.
25.【解答】解:操作一,∵四边形ABCD为矩形,
∴∠A=∠D=90°.
∵将矩形纸片折叠,使点A落在CD边上,点A的对应点为点E,折痕为FG,
∴△AFG≌△EFG,
∴AF=EF,
∵AD=10,
∴DF=AD﹣AF.
在Rt△DEF中,
∵DF2+DE2=EF2,
∴DE.
故答案为:;
操作二:①四边形AGEF的形状是菱形,理由:
∵FG为折痕,
∴点A与点E关于FG对称,
∴FG垂直平分AE,
∴FG⊥AE,AO=OE.
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠FEO=∠GAO.
在△EFO和△AGO中,
,
∴△EFO≌△AGO(ASA),
∴FO=GO,FE=GA.
∵FE∥GA,
∴四边形AGEF为平行四边形,
∵FG⊥AE,
∴四边形AGEF是菱形;
②连结OD′,过点O作OH⊥BC于点H,如图,
则OD′=OH.
∵四边形ABCD为矩形,
∴AB⊥BC,DC⊥BC,
∵OH⊥BC,
∴AB∥OH∥CD,
由①知:AO=OE,
∴OH为梯形ABCE的中位线,
∴EC+AB=2OH,
∴EC+AB=2OD′.
设DE=x,则EC=20﹣x,
∴AE.
由题意得:∠D=∠D′=90°,
∵AO=OE,
∴D′O为Rt△AD′E斜边上的中线,
∴D′OAE,
∴OH=OD′AE,
∴20+20﹣x=2,
∴x.
∴DE.
故答案为:.
第1页(共1页)
