5.7用二元一次方程组确定一次函数表达式 同步训练(无答案)2023--2024学年北师大版八年级数学 上册
文档属性
| 名称 | 5.7用二元一次方程组确定一次函数表达式 同步训练(无答案)2023--2024学年北师大版八年级数学 上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 303.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 01:27:08 | ||
图片预览


文档简介
5.7用二元一次方程组确定一次函数表达式
一、选择题。
1.若关于,的二元一次方程组的解为,一次函数与的图象的交点坐标为( )
A. B. C. D.
2.若二元一次方程组的解为,则直线y=﹣3x+a和y=2x﹣( )
A.(n,m) B.(m,m) C.(m,n) D.(n,n)
3.以二元一次方程的解为坐标的点组成的图象画在坐标系中可能是( )
A. B.
C. D.
4.在平面直角坐标系中,点,以为一边在第一象限内作正方形,则对角线所在直线的解析式为
A. B. C. D.
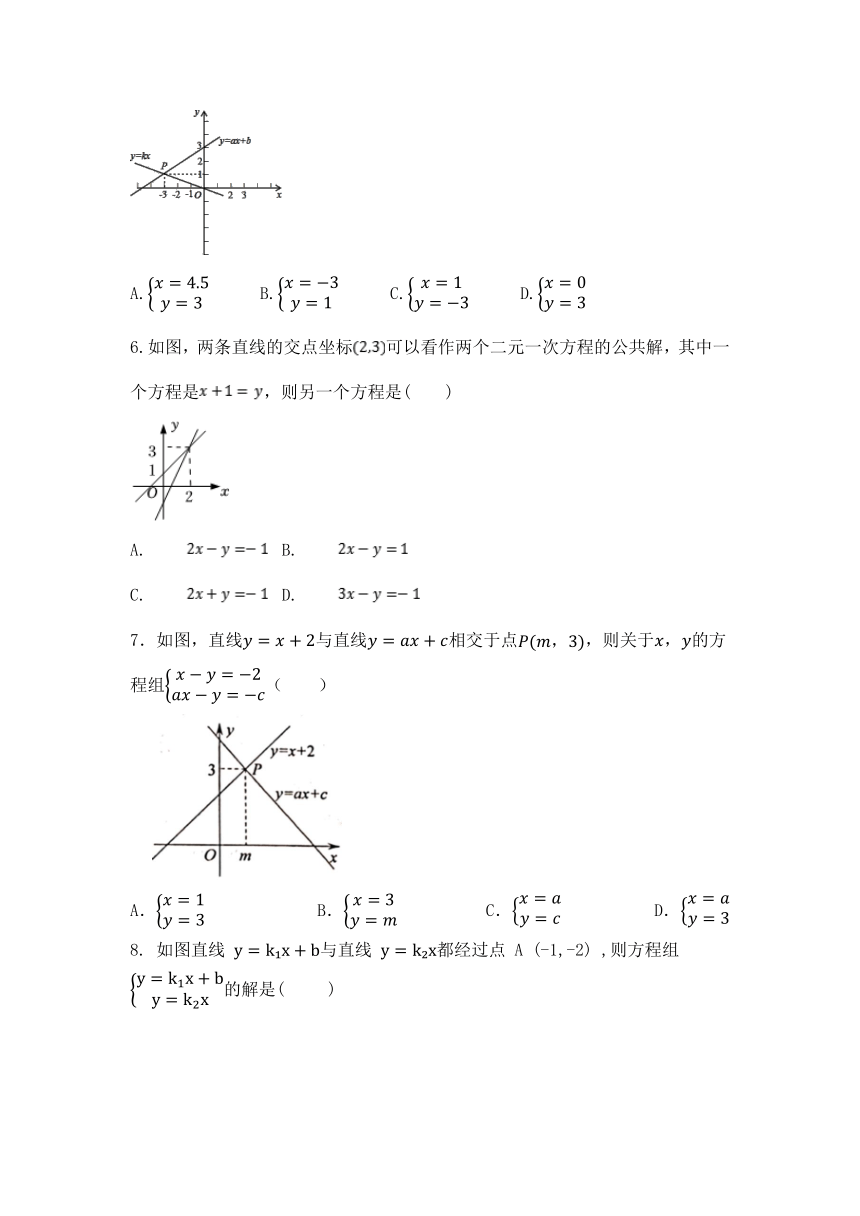
5.如图,已知函数=和=的图象交于点,则根据图象可得,关于、的二元一次方程组的解是( )
A. B. C. D.
6.如图,两条直线的交点坐标可以看作两个二元一次方程的公共解,其中一个方程是,则另一个方程是( )
A. B.
C. D.
7.如图,直线与直线相交于点,则关于,的方程组( )
A. B. C. D.
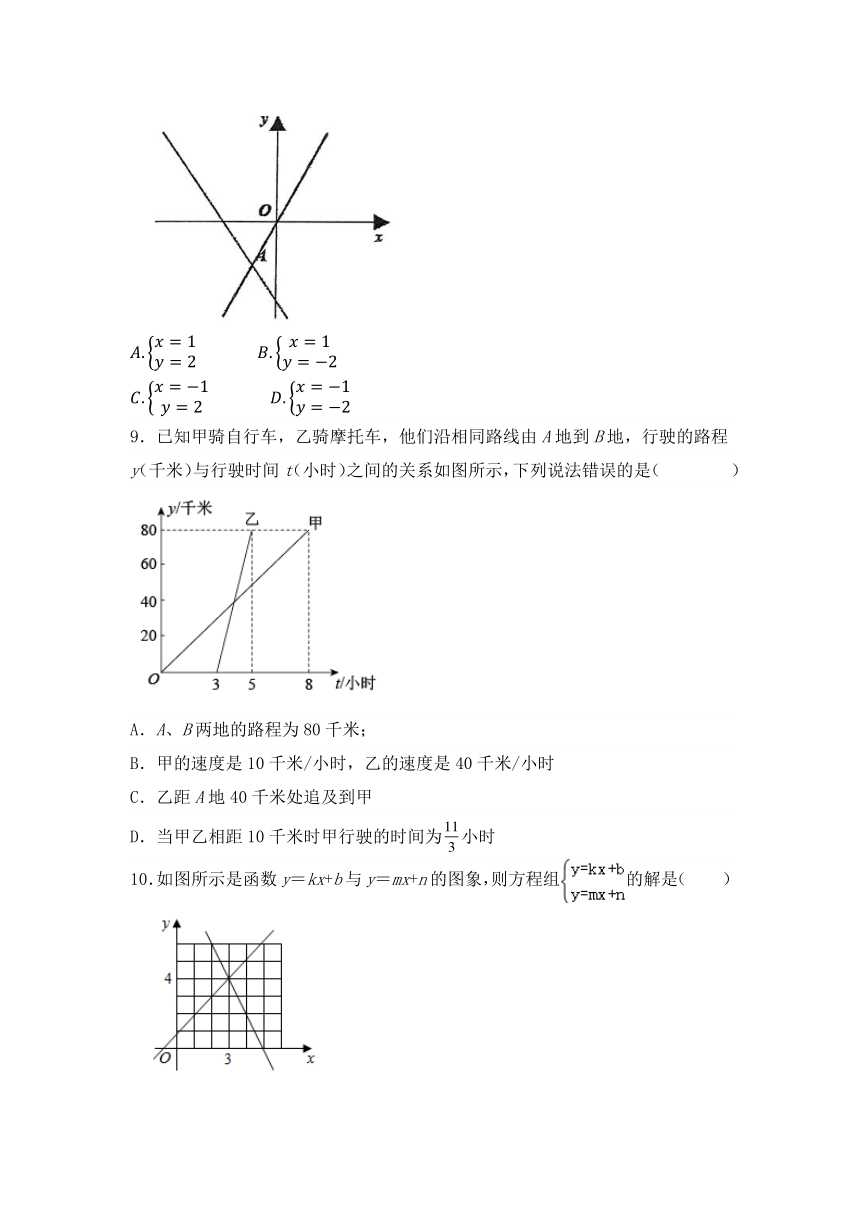
8. 如图直线 与直线 都经过点 A (-1,-2) ,则方程组 的解是( )
9.已知甲骑自行车,乙骑摩托车,他们沿相同路线由A地到B地,行驶的路程y(千米)与行驶时间t(小时)之间的关系如图所示,下列说法错误的是( )
A.A、B两地的路程为80千米;
B.甲的速度是10千米/小时,乙的速度是40千米/小时
C.乙距A地40千米处追及到甲
D.当甲乙相距10千米时甲行驶的时间为小时
10.如图所示是函数y=kx+b与y=mx+n的图象,则方程组的解是( )
A. B. C. D.
11.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为( )
A. B. C. D.
12.在平面直角坐标系xOy中,一次函数y=kx和y=﹣x+3的图象如图所示,则二元一次方程组的解是( )
A. B. C. D.
二、填空题。
1. 在平面直角坐标系中,方程2x+3y=4所对应的直线为 a,方程3x+2y=4所对应的直线为b,直线a与b的交点坐标为 .
2.已知一次函数y=﹣x+m和y=x+n的图象都经过A(﹣2,0),则A点可看作方程组 的解.
3.已知二元一次方程组无解,则直线与的位置关系是__________.
4.某市为提倡居民节约用水,自今年月日起调整居民用水价格图中、分别表示去年、今年水费元与用水量之间的关系小雨家去年用水量为,若今年用水量与去年相同,则水费将比去年多 元
5.如图,已知函数y=ax+b和y=kx的图象交于点P,根据图象可得,二元一次方程组的解是 .
6.如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组的解是 .
三、解答题。
1.如图,直线经过原点和点,点B坐标为
(1)求直线l所对应的函数解析式;
(2)若P为射线上的一点,设P点横坐标为,的面积为,写出关于的函数解析式,指出自变量x的取值范围.
2.如图,直线l1:y=x+5交y轴,x轴于A,B两点,直线l2:y=﹣x﹣1交y轴,x轴于C,D两点,直线l1,l2相交于P点.
(1)方程组的解是 ;
(2)求直线l1,l2与x轴围成的三角形面积;
(3)过P点的直线把△PAC面积两等分,直接写出这条直线的解析式.
3.已知点P(x,y)在第一象限,且x+y=7,点A的坐标为(6,0),设△OPA的面积为S.
(1)用含x的代数式表示S,则S= ,自变量x的取值范围是 ;
(2)建立平面直角坐标系,画出函数S关于自变量x的图象;
(3)当△OPA的面积为18时,求点P的坐标.
4.如图,直线的函数表达式为,且直线与轴交于点.直线与轴交于点,且经过点,直线与交于点.
(1)求点和点的坐标;
(2)求直线的函数表达式;
(3)利用函数图象写出关于,的二元一次方程组的解.
5.如图,已知函数和的图象交于点,点的横坐标为1,
(1)关于,的方程组的解是 ;
(2) ;
(3)求出函数和的图象与轴围成的几何图形的面积.
6.某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费元与每月的用水量立方米之间的关系如图所示.
求关于的函数表达式;
若某用户二、三月份共用水立方米二月份的用水量不超过立方米,缴纳水费元,则该用户二、三月份的用水量各是多少立方米?
一、选择题。
1.若关于,的二元一次方程组的解为,一次函数与的图象的交点坐标为( )
A. B. C. D.
2.若二元一次方程组的解为,则直线y=﹣3x+a和y=2x﹣( )
A.(n,m) B.(m,m) C.(m,n) D.(n,n)
3.以二元一次方程的解为坐标的点组成的图象画在坐标系中可能是( )
A. B.
C. D.
4.在平面直角坐标系中,点,以为一边在第一象限内作正方形,则对角线所在直线的解析式为
A. B. C. D.
5.如图,已知函数=和=的图象交于点,则根据图象可得,关于、的二元一次方程组的解是( )
A. B. C. D.
6.如图,两条直线的交点坐标可以看作两个二元一次方程的公共解,其中一个方程是,则另一个方程是( )
A. B.
C. D.
7.如图,直线与直线相交于点,则关于,的方程组( )
A. B. C. D.
8. 如图直线 与直线 都经过点 A (-1,-2) ,则方程组 的解是( )
9.已知甲骑自行车,乙骑摩托车,他们沿相同路线由A地到B地,行驶的路程y(千米)与行驶时间t(小时)之间的关系如图所示,下列说法错误的是( )
A.A、B两地的路程为80千米;
B.甲的速度是10千米/小时,乙的速度是40千米/小时
C.乙距A地40千米处追及到甲
D.当甲乙相距10千米时甲行驶的时间为小时
10.如图所示是函数y=kx+b与y=mx+n的图象,则方程组的解是( )
A. B. C. D.
11.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为( )
A. B. C. D.
12.在平面直角坐标系xOy中,一次函数y=kx和y=﹣x+3的图象如图所示,则二元一次方程组的解是( )
A. B. C. D.
二、填空题。
1. 在平面直角坐标系中,方程2x+3y=4所对应的直线为 a,方程3x+2y=4所对应的直线为b,直线a与b的交点坐标为 .
2.已知一次函数y=﹣x+m和y=x+n的图象都经过A(﹣2,0),则A点可看作方程组 的解.
3.已知二元一次方程组无解,则直线与的位置关系是__________.
4.某市为提倡居民节约用水,自今年月日起调整居民用水价格图中、分别表示去年、今年水费元与用水量之间的关系小雨家去年用水量为,若今年用水量与去年相同,则水费将比去年多 元
5.如图,已知函数y=ax+b和y=kx的图象交于点P,根据图象可得,二元一次方程组的解是 .
6.如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组的解是 .
三、解答题。
1.如图,直线经过原点和点,点B坐标为
(1)求直线l所对应的函数解析式;
(2)若P为射线上的一点,设P点横坐标为,的面积为,写出关于的函数解析式,指出自变量x的取值范围.
2.如图,直线l1:y=x+5交y轴,x轴于A,B两点,直线l2:y=﹣x﹣1交y轴,x轴于C,D两点,直线l1,l2相交于P点.
(1)方程组的解是 ;
(2)求直线l1,l2与x轴围成的三角形面积;
(3)过P点的直线把△PAC面积两等分,直接写出这条直线的解析式.
3.已知点P(x,y)在第一象限,且x+y=7,点A的坐标为(6,0),设△OPA的面积为S.
(1)用含x的代数式表示S,则S= ,自变量x的取值范围是 ;
(2)建立平面直角坐标系,画出函数S关于自变量x的图象;
(3)当△OPA的面积为18时,求点P的坐标.
4.如图,直线的函数表达式为,且直线与轴交于点.直线与轴交于点,且经过点,直线与交于点.
(1)求点和点的坐标;
(2)求直线的函数表达式;
(3)利用函数图象写出关于,的二元一次方程组的解.
5.如图,已知函数和的图象交于点,点的横坐标为1,
(1)关于,的方程组的解是 ;
(2) ;
(3)求出函数和的图象与轴围成的几何图形的面积.
6.某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费元与每月的用水量立方米之间的关系如图所示.
求关于的函数表达式;
若某用户二、三月份共用水立方米二月份的用水量不超过立方米,缴纳水费元,则该用户二、三月份的用水量各是多少立方米?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
