第二十二章二次函数期末章节巩固练习 2023-2024学年人教版(2012)数学九年级上册(含答案)
文档属性
| 名称 | 第二十二章二次函数期末章节巩固练习 2023-2024学年人教版(2012)数学九年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 301.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 08:10:05 | ||
图片预览



文档简介
人教版(2012)数学九年级上册第二十二章二次函数期末章节巩固练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将二次函数y=x2﹣3的图象向下平移2个单位长度后,所得图象的解析式是( )
A.y=x2﹣5 B.y=x2﹣3 C.y=(x+2)2﹣3 D.y=(x﹣2)2﹣3
2.二次函数的自变量与函数值的部分对应值如下表:
… -3 -2 -1 0 1 …
… -11 -3 1 1 -3 …
对于下列结论:①二次函数的图像开口向下;②当时,随的增大而减小;③二次函数的最大值是1;④若,是二次函数图像与轴交点的横坐标,则,其中,正确的是( )
A.①② B.③④ C.①③ D.①②④
3.将抛物线向左平移2个单位,得到抛物线的解析式是( )
A. B. C. D.
4.若二次函数y=x2+2x+1在m≤x≤m+1(m为常数)的范围内有最小值1,则m的值为( )
A.﹣3或0 B.﹣2或1 C.﹣2或0 D.﹣3≤m≤﹣2
5.已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,则正确的结论是( )
A.①②③④ B.②④⑤
C.②③④ D.①④⑤
6.将抛物线y=2(x+1)2﹣2向右平移2个单位,再向上平移2个单位所得新抛物线的表达式是( )
A.y=2(x+3)2 B.y=(x+3)2 C.y=(x﹣1)2 D.y=2(x﹣1)2
7.关于x的方程a(x+h)2+k=0的解是x1=-2,x2=1(a,h,k均为常数,a)则方程a(x+h+2)2+k=0的解是( )
A.x1=-2,x2=1 B.x1=-4,x2=-1 C.x1=0,x2=2 D.x1=2,x2=-1
8.抛物线的顶点坐标是( )
A.(0,3) B.(1,3) C.(-1,-3) D.(2,-3)
9.下列函数中是二次函数的是( )
A. B. C. D.
10.将二次函数的图象先向右平移1个单位,再向上平移1个单位后顶点为( )
A.(0,1) B.(2,1) C.(1,-1) D.(-2,1)
二、填空题
11.在平面直角坐标系中,若将抛物线y=2x2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是 .
12.如图,在中,,,为边上的高,动点在上,从点出发,沿方向运动,设,的面积为,矩形的面积为,,则与的关系式是 .
13.已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是 .
14.已知抛物线,则这条抛物线的对称轴是直线 .
15.正方形ABCD,边长为4,E是边BC上的一动点,连DE,取DE中点G,将GE绕E顺时针旋转90°到EF,连接CF,当CE为 时,CF取得最小值.
16.已知二次函数,如果当x=-1时y=2,那么当x=2时,y= .
17.如图,过x轴上一点A作平行于y轴的直线分别与抛物线及交于B、C两点,若正方形的一边与y轴重合,则此正方形的面积为 .
18.已知二次函数中,函数y与自变量x的部分对应值如表:则当时,x的取值范围是 .
x … -1 0 1 2 3 …
y … 4 0 -1 m 4 …
19.抛物线y=﹣x2+4x的对称轴是 .
20.(1)分解因式: ;
(2)抛物线 与 轴的交点的坐标是 .
三、解答题
21.某公司生产的某种时令商品每件成本为元,经过市场调研发现,这种商品在未来天内的日销售量(件)与(天)的关系如表:
时间(天)
日销售量(件)
未来天内,前天每天的价格(且为整数),后天每天的价格(且为整数).
(1)认真分析上表中的数据,用所学过的知一次函数,二次函数的知识确定一个满足这些数据(件)与(天)之间的关系式,求出日销售量(件)与(天)之间的函数关系式;
(2)请预测未来天中哪一天的日销售利润最大,最大日销售利润是多少?
22.一款服装每件进价为80元,销售价为120元时,每天可售出20件.经市场调查发现,如果每件服装降价1元,那么平均每天可多售出2件.设每件服装降价x元,
(1)则每天销售量增加________件,每件服装盈利________元(用含x的代数式表示);
(2)在让利于顾客的情况下,每件服装降价多少元时,商家平均每天能盈利1200元?
(3)求其最大利润.
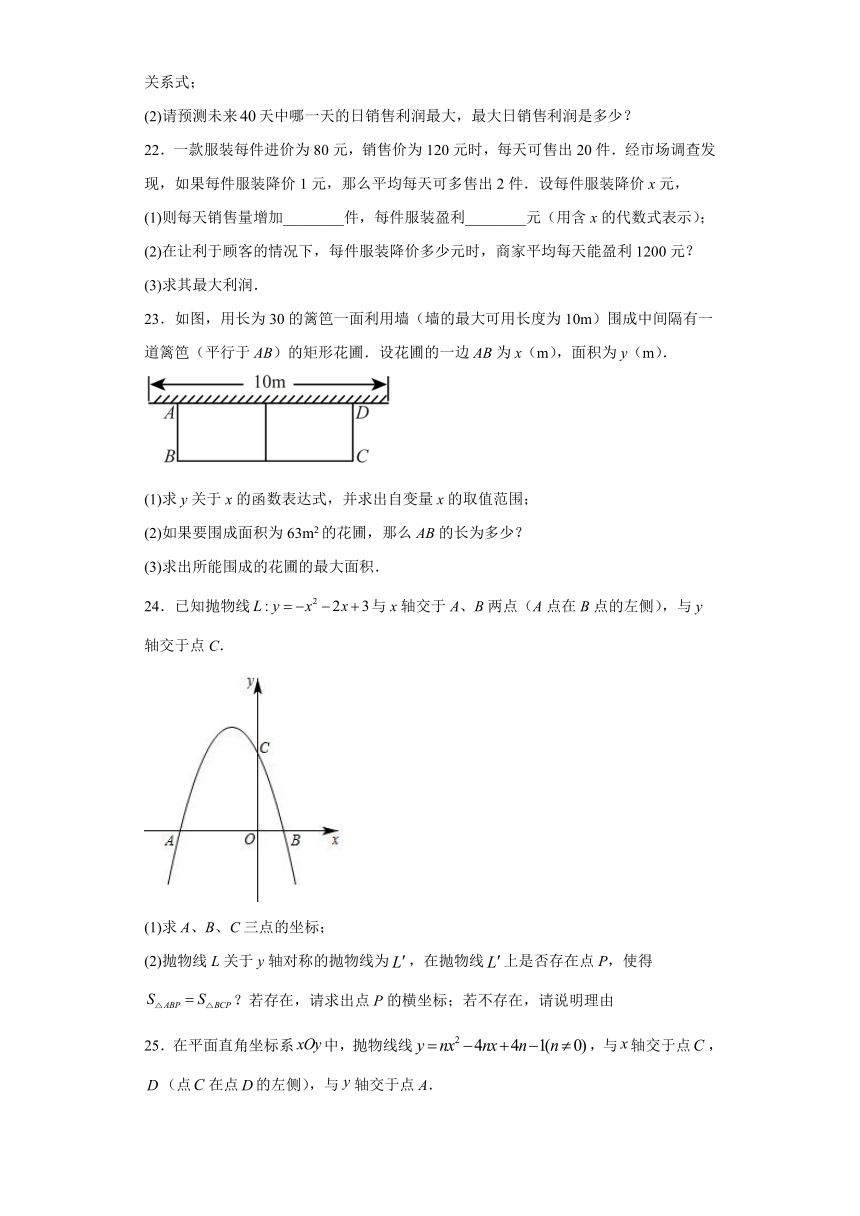
23.如图,用长为30的篱笆一面利用墙(墙的最大可用长度为10m)围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为x(m),面积为y(m).
(1)求y关于x的函数表达式,并求出自变量x的取值范围;
(2)如果要围成面积为63m2的花圃,那么AB的长为多少?
(3)求出所能围成的花圃的最大面积.
24.已知抛物线与x轴交于A、B两点(A点在B点的左侧),与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)抛物线L关于y轴对称的抛物线为,在抛物线上是否存在点P,使得?若存在,请求出点P的横坐标;若不存在,请说明理由
25.在平面直角坐标系中,抛物线线,与轴交于点,(点在点的左侧),与轴交于点A.
(1)求抛物线顶点的坐标.
(2)若点A的坐标为,轴,交抛物线于点,求点的坐标.
26.已知函数.
(1)指出函数图象的开口方向、对称轴和顶点坐标;
(2)当取何值时该函数有最值,并求出最值.
(3)当取何值时,随的增大而减小.
27.已知二次函数的图像与x轴交于点,与y轴交于点C,且,求二次函数的解析式.
参考答案:
1.A
2.A
3.A
4.A
5.D
6.D
7.B
8.A
9.D
10.B
11.(4,3)
12.
13..
14.
15.
16.8
17.4
18./
19.直线x=2
20. ; ,
21.(1)
(2)第天的日销售利润最大为元
22.(1),
(2)元
(3)
23.(1)
(2)7m
(3)m2
24.(1),,
(2)存在,点P的横坐标为或或或
25.(1);
(2);
26.(1)开口向下,顶点坐标为,对称轴为直线
(2)当时,函数有最大值
(3)当,随x的增大而减小
27.或
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将二次函数y=x2﹣3的图象向下平移2个单位长度后,所得图象的解析式是( )
A.y=x2﹣5 B.y=x2﹣3 C.y=(x+2)2﹣3 D.y=(x﹣2)2﹣3
2.二次函数的自变量与函数值的部分对应值如下表:
… -3 -2 -1 0 1 …
… -11 -3 1 1 -3 …
对于下列结论:①二次函数的图像开口向下;②当时,随的增大而减小;③二次函数的最大值是1;④若,是二次函数图像与轴交点的横坐标,则,其中,正确的是( )
A.①② B.③④ C.①③ D.①②④
3.将抛物线向左平移2个单位,得到抛物线的解析式是( )
A. B. C. D.
4.若二次函数y=x2+2x+1在m≤x≤m+1(m为常数)的范围内有最小值1,则m的值为( )
A.﹣3或0 B.﹣2或1 C.﹣2或0 D.﹣3≤m≤﹣2
5.已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,则正确的结论是( )
A.①②③④ B.②④⑤
C.②③④ D.①④⑤
6.将抛物线y=2(x+1)2﹣2向右平移2个单位,再向上平移2个单位所得新抛物线的表达式是( )
A.y=2(x+3)2 B.y=(x+3)2 C.y=(x﹣1)2 D.y=2(x﹣1)2
7.关于x的方程a(x+h)2+k=0的解是x1=-2,x2=1(a,h,k均为常数,a)则方程a(x+h+2)2+k=0的解是( )
A.x1=-2,x2=1 B.x1=-4,x2=-1 C.x1=0,x2=2 D.x1=2,x2=-1
8.抛物线的顶点坐标是( )
A.(0,3) B.(1,3) C.(-1,-3) D.(2,-3)
9.下列函数中是二次函数的是( )
A. B. C. D.
10.将二次函数的图象先向右平移1个单位,再向上平移1个单位后顶点为( )
A.(0,1) B.(2,1) C.(1,-1) D.(-2,1)
二、填空题
11.在平面直角坐标系中,若将抛物线y=2x2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是 .
12.如图,在中,,,为边上的高,动点在上,从点出发,沿方向运动,设,的面积为,矩形的面积为,,则与的关系式是 .
13.已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是 .
14.已知抛物线,则这条抛物线的对称轴是直线 .
15.正方形ABCD,边长为4,E是边BC上的一动点,连DE,取DE中点G,将GE绕E顺时针旋转90°到EF,连接CF,当CE为 时,CF取得最小值.
16.已知二次函数,如果当x=-1时y=2,那么当x=2时,y= .
17.如图,过x轴上一点A作平行于y轴的直线分别与抛物线及交于B、C两点,若正方形的一边与y轴重合,则此正方形的面积为 .
18.已知二次函数中,函数y与自变量x的部分对应值如表:则当时,x的取值范围是 .
x … -1 0 1 2 3 …
y … 4 0 -1 m 4 …
19.抛物线y=﹣x2+4x的对称轴是 .
20.(1)分解因式: ;
(2)抛物线 与 轴的交点的坐标是 .
三、解答题
21.某公司生产的某种时令商品每件成本为元,经过市场调研发现,这种商品在未来天内的日销售量(件)与(天)的关系如表:
时间(天)
日销售量(件)
未来天内,前天每天的价格(且为整数),后天每天的价格(且为整数).
(1)认真分析上表中的数据,用所学过的知一次函数,二次函数的知识确定一个满足这些数据(件)与(天)之间的关系式,求出日销售量(件)与(天)之间的函数关系式;
(2)请预测未来天中哪一天的日销售利润最大,最大日销售利润是多少?
22.一款服装每件进价为80元,销售价为120元时,每天可售出20件.经市场调查发现,如果每件服装降价1元,那么平均每天可多售出2件.设每件服装降价x元,
(1)则每天销售量增加________件,每件服装盈利________元(用含x的代数式表示);
(2)在让利于顾客的情况下,每件服装降价多少元时,商家平均每天能盈利1200元?
(3)求其最大利润.
23.如图,用长为30的篱笆一面利用墙(墙的最大可用长度为10m)围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为x(m),面积为y(m).
(1)求y关于x的函数表达式,并求出自变量x的取值范围;
(2)如果要围成面积为63m2的花圃,那么AB的长为多少?
(3)求出所能围成的花圃的最大面积.
24.已知抛物线与x轴交于A、B两点(A点在B点的左侧),与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)抛物线L关于y轴对称的抛物线为,在抛物线上是否存在点P,使得?若存在,请求出点P的横坐标;若不存在,请说明理由
25.在平面直角坐标系中,抛物线线,与轴交于点,(点在点的左侧),与轴交于点A.
(1)求抛物线顶点的坐标.
(2)若点A的坐标为,轴,交抛物线于点,求点的坐标.
26.已知函数.
(1)指出函数图象的开口方向、对称轴和顶点坐标;
(2)当取何值时该函数有最值,并求出最值.
(3)当取何值时,随的增大而减小.
27.已知二次函数的图像与x轴交于点,与y轴交于点C,且,求二次函数的解析式.
参考答案:
1.A
2.A
3.A
4.A
5.D
6.D
7.B
8.A
9.D
10.B
11.(4,3)
12.
13..
14.
15.
16.8
17.4
18./
19.直线x=2
20. ; ,
21.(1)
(2)第天的日销售利润最大为元
22.(1),
(2)元
(3)
23.(1)
(2)7m
(3)m2
24.(1),,
(2)存在,点P的横坐标为或或或
25.(1);
(2);
26.(1)开口向下,顶点坐标为,对称轴为直线
(2)当时,函数有最大值
(3)当,随x的增大而减小
27.或
同课章节目录
