第四章几何图形初步 期末章节巩固练习 2023-2024学年人教版(2012)数学七年级上册 (含答案)
文档属性
| 名称 | 第四章几何图形初步 期末章节巩固练习 2023-2024学年人教版(2012)数学七年级上册 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 526.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 00:00:00 | ||
图片预览



文档简介
人教版(2012)数学七年级上册第四章几何图形初步期末章节巩固练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
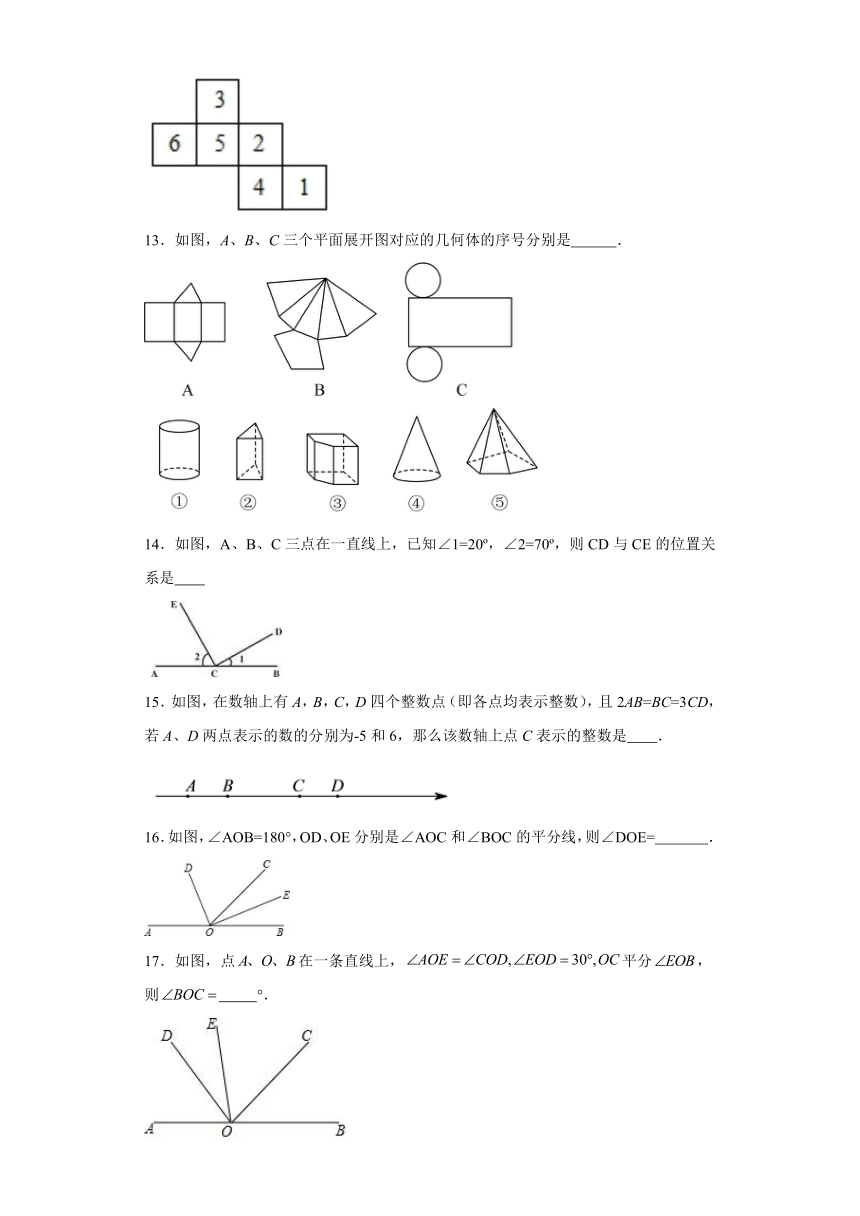
1.圆柱的表面展开图可能是( )
A. B. C. D.
2.下列几何体中,可以由平面图形绕某条直线旋转一周得到的是( )
A. B. C. D.
3.下列图形经过折叠不能围成一个棱柱的是( )
A. B. C. D.
4.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“疫”字所在面相对的面上的汉字是( )
A.春 B.散 C.去 D.情
5.下列说法中正确的有( )
①过两点有且只有一条直线
②连接两点的线段叫做两点间的距离
③两点之间,线段最短
④若AB=BC,则点B是AC的中点
⑤射线AC和射线CA是同一条射线
A.1个 B.2个 C.3个 D.4个
6.如图是一个正方体的表面展开图,则原正方体中与“寄”字所在面相对的面上标的字是( )
A.华 B.一 C.学 D.校
7.如图,,为线段上的两点,,是线段的中点,若,则的长是( )
A. B. C. D.
8.下列叙述正确的是( )
A.延长直线到点C B.和互为余角
C.5.1625精确到百分位是5.163 D.两点之间,直线最短
9.在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②在砌墙前,师傅会在墙两端拉一根笔直的水平线;③把弯曲的公路改直;④植树时栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①② B.①②④ C.①④ D.①②③
10.已知∠AOB=30°,又自∠AOB的顶点O引射线OC.若∠AOC:∠AOB=4:3,那么∠BOC= ( )
A.10° B.40° C.45° D.70°或10°
二、填空题
11.和互补,且,则 ,理由是 .
12.如图是正方体的表面展开图,则原正方体“4”与相对面上的数字之和是 .
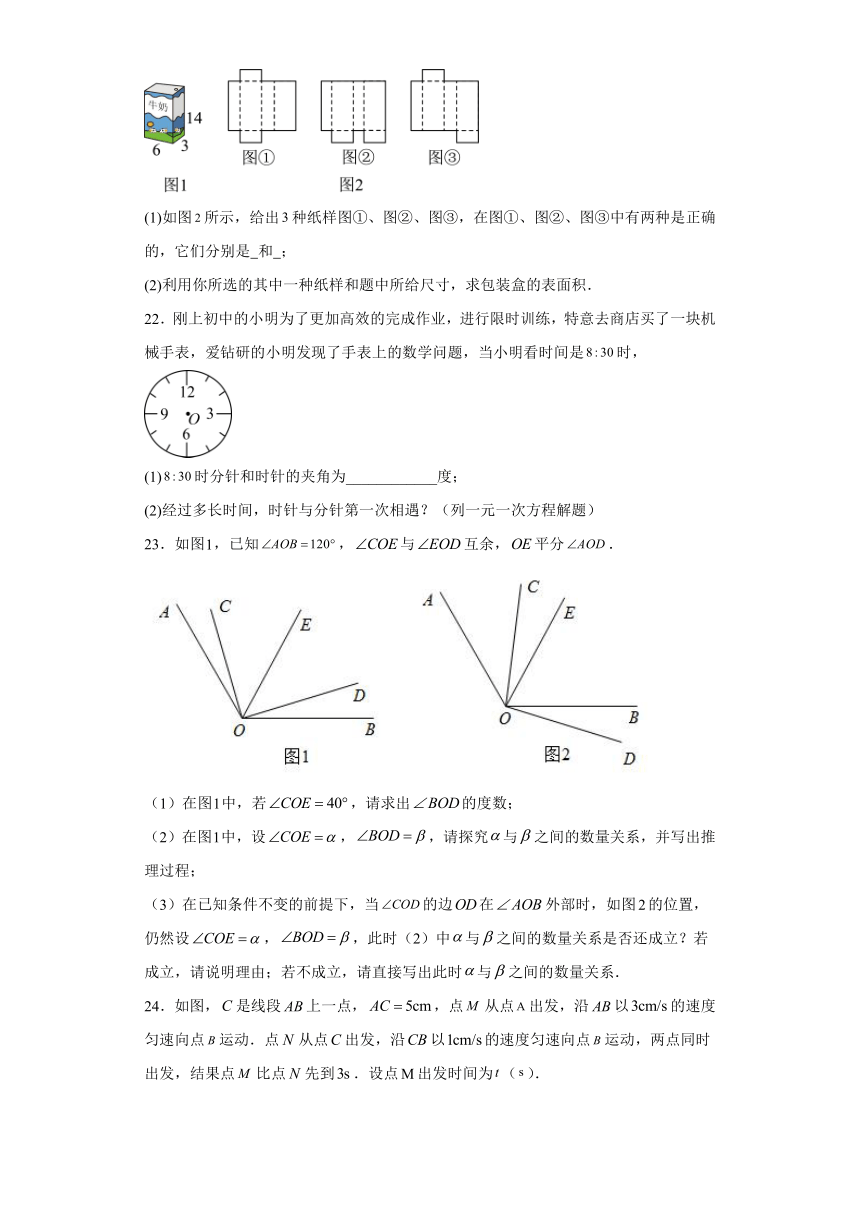
13.如图,A、B、C三个平面展开图对应的几何体的序号分别是 .
14.如图,A、B、C三点在一直线上,已知∠1=20 ,∠2=70 ,则CD与CE的位置关系是
15.如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数的分别为-5和6,那么该数轴上点C表示的整数是 .
16.如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠DOE= .
17.如图,点在一条直线上,平分,则 °.
18.点O为直线l上一点,射线OA、OB均与直线l重合,将射线OB绕点O逆时针旋转α(0≤α≤90°),过点O作射线OC、OD、OM、ON,使得∠BOC=90°,∠COD=2α,∠COM=∠AOC,∠CON=∠COD(OM在∠AOC内部,ON在∠COD内部),当∠MON=α时,则α= .
19.如图,是直线上的一点,是一条射线,平分,在内,且,.下列四个结论:①;②射线平分;③图中与互余的角有2个;④图中互补的角有5对.其中结论正确的序号有 .
20.如图,∠AOB=72,射线OC将∠AOB分成两个角,且∠AOC:∠BOC=1:2,则∠BOC= .
三、解答题
21.有一种纯牛奶包装盒及其尺寸如图所示.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图所示,给出种纸样图①、图②、图③,在图①、图②、图③中有两种是正确的,它们分别是 和 ;
(2)利用你所选的其中一种纸样和题中所给尺寸,求包装盒的表面积.
22.刚上初中的小明为了更加高效的完成作业,进行限时训练,特意去商店买了一块机械手表,爱钻研的小明发现了手表上的数学问题,当小明看时间是时,
(1)时分针和时针的夹角为____________度;
(2)经过多长时间,时针与分针第一次相遇?(列一元一次方程解题)
23.如图,已知,与互余,平分.
(1)在图中,若,请求出的度数;
(2)在图中,设,,请探究与之间的数量关系,并写出推理过程;
(3)在已知条件不变的前提下,当的边在外部时,如图的位置,仍然设,,此时(2)中与之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时与之间的数量关系.
24.如图,是线段上一点,,点从点出发,沿以的速度匀速向点运动.点从点出发,沿以的速度匀速向点运动,两点同时出发,结果点比点先到.设点出发时间为().
(1)求线段的长.
(2)是否存在某个时刻,点恰好是线段的中点?如果存在,请求出的值.若不存在,请说明理由.
(3)求点与点重合时(未到达点),的值;
(4)直接写出点与点相距时,的值.
25.已知,,平分,平分.
(1)如图1,当,重合时,求的值;
(2)如图2,当从图1所示的位置开始绕点以每秒的速度顺时针旋转.在旋转过程中,的值是否会因的变化而变化?若不变化,请求出该定值;若变化,请说明理由;
(3)在(2)的条件下,求当旋转多少秒时,.
26.如图,线段,C是线段上一点,,M是的中点,N是的中点
(1)图中共有 条线段
(2)求线段的长
27.找朋友,手拉手:
用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.
下面所给的三排图形都存在着某种联系,用线将它们连起来
参考答案:
1.D
2.B
3.B
4.B
5.B
6.D
7.C
8.B
9.B
10.D
11. 同角的补角相等
12.
13.②⑤①
14.垂直
15.4
16.90°
17.50°
18.20°/20度
19.①②③
20.48°
21.(1)图①,图③
(2)288
22.(1)75
(2)分钟
23.(1),(2);(3)不成立,此时与之间的数量关系为:,
24.(1);
(2)存在某个时刻,点恰好是线段的中点,;
(3)
(4)或.
25.(1)
(2)不变,
(3)
26.(1)10
(2)
27.略
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.圆柱的表面展开图可能是( )
A. B. C. D.
2.下列几何体中,可以由平面图形绕某条直线旋转一周得到的是( )
A. B. C. D.
3.下列图形经过折叠不能围成一个棱柱的是( )
A. B. C. D.
4.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“疫”字所在面相对的面上的汉字是( )
A.春 B.散 C.去 D.情
5.下列说法中正确的有( )
①过两点有且只有一条直线
②连接两点的线段叫做两点间的距离
③两点之间,线段最短
④若AB=BC,则点B是AC的中点
⑤射线AC和射线CA是同一条射线
A.1个 B.2个 C.3个 D.4个
6.如图是一个正方体的表面展开图,则原正方体中与“寄”字所在面相对的面上标的字是( )
A.华 B.一 C.学 D.校
7.如图,,为线段上的两点,,是线段的中点,若,则的长是( )
A. B. C. D.
8.下列叙述正确的是( )
A.延长直线到点C B.和互为余角
C.5.1625精确到百分位是5.163 D.两点之间,直线最短
9.在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②在砌墙前,师傅会在墙两端拉一根笔直的水平线;③把弯曲的公路改直;④植树时栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①② B.①②④ C.①④ D.①②③
10.已知∠AOB=30°,又自∠AOB的顶点O引射线OC.若∠AOC:∠AOB=4:3,那么∠BOC= ( )
A.10° B.40° C.45° D.70°或10°
二、填空题
11.和互补,且,则 ,理由是 .
12.如图是正方体的表面展开图,则原正方体“4”与相对面上的数字之和是 .
13.如图,A、B、C三个平面展开图对应的几何体的序号分别是 .
14.如图,A、B、C三点在一直线上,已知∠1=20 ,∠2=70 ,则CD与CE的位置关系是
15.如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数的分别为-5和6,那么该数轴上点C表示的整数是 .
16.如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠DOE= .
17.如图,点在一条直线上,平分,则 °.
18.点O为直线l上一点,射线OA、OB均与直线l重合,将射线OB绕点O逆时针旋转α(0≤α≤90°),过点O作射线OC、OD、OM、ON,使得∠BOC=90°,∠COD=2α,∠COM=∠AOC,∠CON=∠COD(OM在∠AOC内部,ON在∠COD内部),当∠MON=α时,则α= .
19.如图,是直线上的一点,是一条射线,平分,在内,且,.下列四个结论:①;②射线平分;③图中与互余的角有2个;④图中互补的角有5对.其中结论正确的序号有 .
20.如图,∠AOB=72,射线OC将∠AOB分成两个角,且∠AOC:∠BOC=1:2,则∠BOC= .
三、解答题
21.有一种纯牛奶包装盒及其尺寸如图所示.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图所示,给出种纸样图①、图②、图③,在图①、图②、图③中有两种是正确的,它们分别是 和 ;
(2)利用你所选的其中一种纸样和题中所给尺寸,求包装盒的表面积.
22.刚上初中的小明为了更加高效的完成作业,进行限时训练,特意去商店买了一块机械手表,爱钻研的小明发现了手表上的数学问题,当小明看时间是时,
(1)时分针和时针的夹角为____________度;
(2)经过多长时间,时针与分针第一次相遇?(列一元一次方程解题)
23.如图,已知,与互余,平分.
(1)在图中,若,请求出的度数;
(2)在图中,设,,请探究与之间的数量关系,并写出推理过程;
(3)在已知条件不变的前提下,当的边在外部时,如图的位置,仍然设,,此时(2)中与之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时与之间的数量关系.
24.如图,是线段上一点,,点从点出发,沿以的速度匀速向点运动.点从点出发,沿以的速度匀速向点运动,两点同时出发,结果点比点先到.设点出发时间为().
(1)求线段的长.
(2)是否存在某个时刻,点恰好是线段的中点?如果存在,请求出的值.若不存在,请说明理由.
(3)求点与点重合时(未到达点),的值;
(4)直接写出点与点相距时,的值.
25.已知,,平分,平分.
(1)如图1,当,重合时,求的值;
(2)如图2,当从图1所示的位置开始绕点以每秒的速度顺时针旋转.在旋转过程中,的值是否会因的变化而变化?若不变化,请求出该定值;若变化,请说明理由;
(3)在(2)的条件下,求当旋转多少秒时,.
26.如图,线段,C是线段上一点,,M是的中点,N是的中点
(1)图中共有 条线段
(2)求线段的长
27.找朋友,手拉手:
用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.
下面所给的三排图形都存在着某种联系,用线将它们连起来
参考答案:
1.D
2.B
3.B
4.B
5.B
6.D
7.C
8.B
9.B
10.D
11. 同角的补角相等
12.
13.②⑤①
14.垂直
15.4
16.90°
17.50°
18.20°/20度
19.①②③
20.48°
21.(1)图①,图③
(2)288
22.(1)75
(2)分钟
23.(1),(2);(3)不成立,此时与之间的数量关系为:,
24.(1);
(2)存在某个时刻,点恰好是线段的中点,;
(3)
(4)或.
25.(1)
(2)不变,
(3)
26.(1)10
(2)
27.略
