2023~2024学年苏科版数学八年级上册 用一次函数的图像解决实际问题 期末复习巩固提升练习 (无答案)
文档属性
| 名称 | 2023~2024学年苏科版数学八年级上册 用一次函数的图像解决实际问题 期末复习巩固提升练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 686.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 08:57:13 | ||
图片预览


文档简介
2023-2024学年苏科版数学八年级上册
期末复习巩固提升练习
(用一次函数的图像解决实际问题)
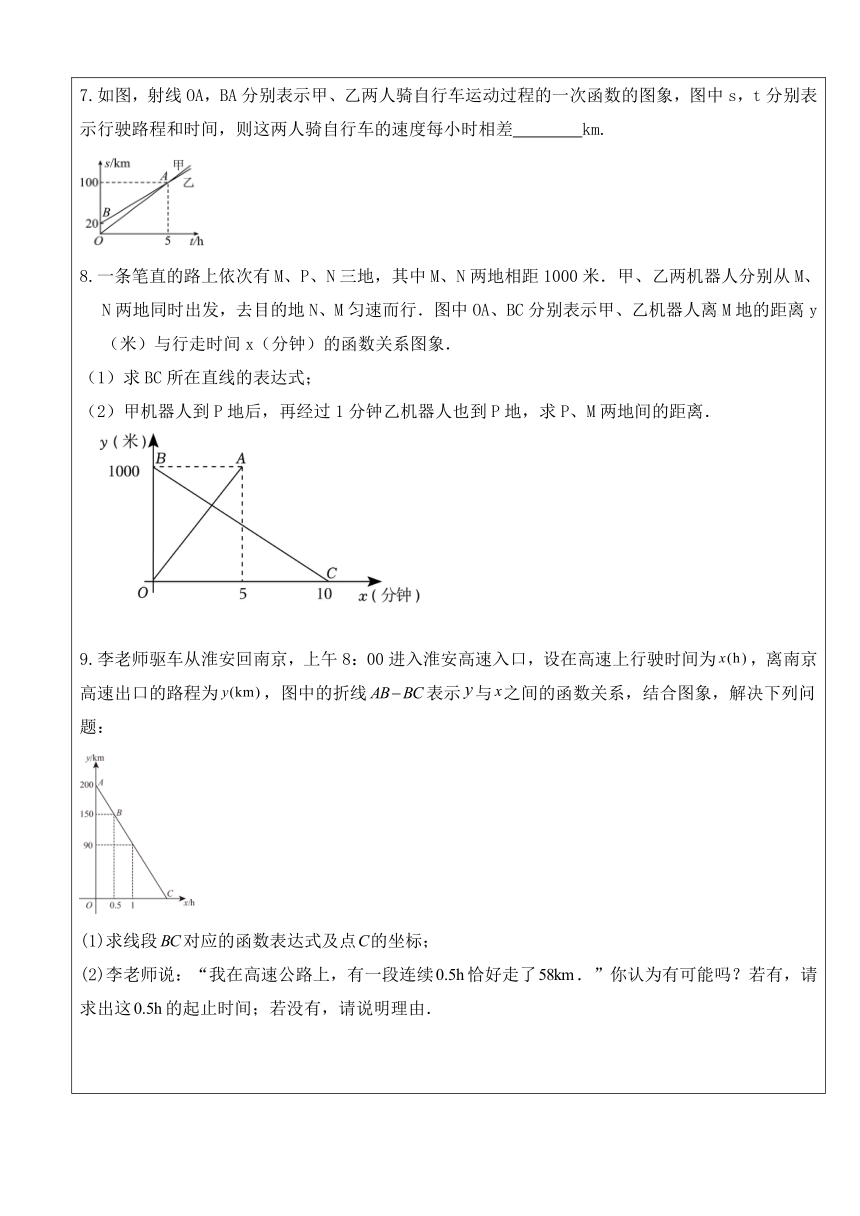
1.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量(单位:升)与时间(单位:分)之间的部分关系如图所示.下列说法错误的是( ) A.每分钟的进水量为5升 B.每分钟的出水量为3.75升 C.从计时开始8分钟时,容器内的水量为25升 D.容器从进水开始到水全部放完的时间是21分钟 2.甲、乙两地之间是一条直路,小红跑步从甲地到乙地,小刚步行从乙地到甲地,两人之间的距离y(单位:米)与小刚步行时间x(单位:分),下列说法错误的是( ) A.小红跑步的速度为米/分 B.小刚步行的速度为米/分 C. D.小红到达乙地时,小刚离甲地还有米 3.如图,某空军加油飞机接到命令,立即给另一架正在飞行的运输机进行空中加油在加油过程中,设运输飞机的油箱余油量为吨,加油飞机的加油箱余油量为吨,加油时间为(分),、与之间的函数图象如图所示,结合图象判断下列说法正确的是 (把正确的序号都填写上) ①加油之前,加油飞机的加油油箱中装载了吨油; ②加油之前,运输飞机的油箱有余油量吨油; ③加油飞机的油全部加给运输飞机需分钟; ④运输飞机加完油后,以原速继续飞行,如果每分钟油耗相同,最多能飞行小时. 一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离 为 千米. 5.如图1,在长方形ABCD中,动点P从点A出发,沿AB﹣BC﹣CD运动,至点D处停止.点P运动的路程为x,△ADP的面积为y,且y与x之间满足的关系如图2所示,则当时,对应的x的值是 . 6.如图1,这是甲、乙两个长方体容器的轴截面示意图,已知甲容器中有一个体积为207cm3的实心圆柱体固定在容器底部,现将甲容器中的水用导管匀速注入乙容器内,在这个过程中,甲、乙两个容器中水的高度h(cm)与注水时间t(min)之间的函数关系如图2所示,则乙容器的底面积是 cm2. 7.如图,射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s,t分别表示行驶路程和时间,则这两人骑自行车的速度每小时相差 km. 8.一条笔直的路上依次有M、P、N三地,其中M、N两地相距1000米.甲、乙两机器人分别从M、N两地同时出发,去目的地N、M匀速而行.图中OA、BC分别表示甲、乙机器人离M地的距离y(米)与行走时间x(分钟)的函数关系图象. (1)求BC所在直线的表达式; (2)甲机器人到P地后,再经过1分钟乙机器人也到P地,求P、M两地间的距离. 9.李老师驱车从淮安回南京,上午8:00进入淮安高速入口,设在高速上行驶时间为,离南京高速出口的路程为,图中的折线表示与之间的函数关系,结合图象,解决下列问题: (1)求线段对应的函数表达式及点的坐标; (2)李老师说:“我在高速公路上,有一段连续恰好走了.”你认为有可能吗?若有,请求出这的起止时间;若没有,请说明理由. 10.小明一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量与行驶时间之间的关系如图所示,根据图象回答下列问题: (1)小汽车行驶________h后加油,中途加油__________L; (2)求加油前油箱余油量Q与行驶时间t的函数关系式;并求t的取值范围; (3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点,车速为,要到达目的地,油箱中的油是否够用?请说明理由. 11.已知甲、乙两地相距千米,小华骑自行车从甲地到乙地,小亮骑摩托车从乙地到甲地再返回乙地.两人同时出发,小华每小时行驶千米,小亮去时用了小时,回来时速度增加了,两人离甲地的距离千米与时间小时的函数关系如图所示. (1)求出小亮与小华第一次相遇时,小华所用的时间以及此时他们离甲地的距离. (2)求出点的坐标及线段所对应的函数关系式;(3)直接写出小华和小亮相距千米时小华骑行的时间. 12.如图1,甲、乙两车分别从相距的、两地相向而行,乙车比甲车先出发小时,并以各自的速度匀速行驶,甲车到达地后因有事立刻按原路原速返回地.乙车从地直达地,两车同时到达地.甲、乙两车距各自出发地的路程(千米)与甲车出发所用的时间(小时)的关系如图,结合图像信息解答下列问题: (1)乙车的速度是 千米/时,乙车行驶 小时到达地; (2)求甲车从地按原路原速返回地的过程中,甲车距它出发地的路程与它出发的时间的函数关系式; (3)求甲车出发多长时间两车相距千米? 13.已知学生公寓、阅览室、超市依次在同一直线上,阅览室离学生公寓1.2,超市离学生公寓2.小明从学生公寓出发,匀速步行了12到阅览室;在阅览室停留70后,匀速步行了10 到超市;在超市停留20后,匀速骑行了8返回学生公寓.给出的图象反映了这个过程中小明离学生公寓的距离y与离开学生公寓的时间x之间的对应关系. 请根据相关信息,解答下列问题: (1)填表: 离开学生公寓的时间/585087112离学生公寓的距离/__________________2
(2)回公寓的路上,小明何时距公寓0.5 ? 14.小明从A地匀速前往B地,同时小亮从B地匀速前往A地,两人离B地的路程与行驶时间之间的函数图像如图所示. (1)A地与B地的距离为 ,小明的速度是 ; (2)求出点P的坐标,并解释其实际意义; (3)设两人之间的距离,在图②中,画出s与x的函数图像(请标出必要的数据); (4)当两人之间的距离小于时,则x的取值范围是 . 15.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费: 第一档是当月用电量不超过240度时实行“基础电价”; 第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费, 超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元. 具体收费情况如折线图所示,请根据图象回答下列问题: (1)“基础电价”是____________元度; (2)求出当x>240时,y与x的函数表达式; (3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度? 16.《九章算术》中记载,浮箭漏(图①)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间,某学校STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究: (实验观察)实验小组通过观察,每2小时记录一次箭尺读数,得到下表: 供水时间x(小时)02468箭尺读数y(厘米)618304254
(1)(探索发现): 若以供水时间x为横轴,箭尺读数y为纵轴,建立平面直角坐标系,描出以表格中数据为坐标的各点,试判断这些点是否在同一条直线上.如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,说明理由. (2)(结论应用)应用上述发现的规律估算:供水时间达到12小时时,箭尺的读数为多少厘米? (3)如果本次实验记录的开始时间是上午8:00,那么当箭尺读数为90厘米时是几点钟?
期末复习巩固提升练习
(用一次函数的图像解决实际问题)
1.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量(单位:升)与时间(单位:分)之间的部分关系如图所示.下列说法错误的是( ) A.每分钟的进水量为5升 B.每分钟的出水量为3.75升 C.从计时开始8分钟时,容器内的水量为25升 D.容器从进水开始到水全部放完的时间是21分钟 2.甲、乙两地之间是一条直路,小红跑步从甲地到乙地,小刚步行从乙地到甲地,两人之间的距离y(单位:米)与小刚步行时间x(单位:分),下列说法错误的是( ) A.小红跑步的速度为米/分 B.小刚步行的速度为米/分 C. D.小红到达乙地时,小刚离甲地还有米 3.如图,某空军加油飞机接到命令,立即给另一架正在飞行的运输机进行空中加油在加油过程中,设运输飞机的油箱余油量为吨,加油飞机的加油箱余油量为吨,加油时间为(分),、与之间的函数图象如图所示,结合图象判断下列说法正确的是 (把正确的序号都填写上) ①加油之前,加油飞机的加油油箱中装载了吨油; ②加油之前,运输飞机的油箱有余油量吨油; ③加油飞机的油全部加给运输飞机需分钟; ④运输飞机加完油后,以原速继续飞行,如果每分钟油耗相同,最多能飞行小时. 一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离 为 千米. 5.如图1,在长方形ABCD中,动点P从点A出发,沿AB﹣BC﹣CD运动,至点D处停止.点P运动的路程为x,△ADP的面积为y,且y与x之间满足的关系如图2所示,则当时,对应的x的值是 . 6.如图1,这是甲、乙两个长方体容器的轴截面示意图,已知甲容器中有一个体积为207cm3的实心圆柱体固定在容器底部,现将甲容器中的水用导管匀速注入乙容器内,在这个过程中,甲、乙两个容器中水的高度h(cm)与注水时间t(min)之间的函数关系如图2所示,则乙容器的底面积是 cm2. 7.如图,射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s,t分别表示行驶路程和时间,则这两人骑自行车的速度每小时相差 km. 8.一条笔直的路上依次有M、P、N三地,其中M、N两地相距1000米.甲、乙两机器人分别从M、N两地同时出发,去目的地N、M匀速而行.图中OA、BC分别表示甲、乙机器人离M地的距离y(米)与行走时间x(分钟)的函数关系图象. (1)求BC所在直线的表达式; (2)甲机器人到P地后,再经过1分钟乙机器人也到P地,求P、M两地间的距离. 9.李老师驱车从淮安回南京,上午8:00进入淮安高速入口,设在高速上行驶时间为,离南京高速出口的路程为,图中的折线表示与之间的函数关系,结合图象,解决下列问题: (1)求线段对应的函数表达式及点的坐标; (2)李老师说:“我在高速公路上,有一段连续恰好走了.”你认为有可能吗?若有,请求出这的起止时间;若没有,请说明理由. 10.小明一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量与行驶时间之间的关系如图所示,根据图象回答下列问题: (1)小汽车行驶________h后加油,中途加油__________L; (2)求加油前油箱余油量Q与行驶时间t的函数关系式;并求t的取值范围; (3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点,车速为,要到达目的地,油箱中的油是否够用?请说明理由. 11.已知甲、乙两地相距千米,小华骑自行车从甲地到乙地,小亮骑摩托车从乙地到甲地再返回乙地.两人同时出发,小华每小时行驶千米,小亮去时用了小时,回来时速度增加了,两人离甲地的距离千米与时间小时的函数关系如图所示. (1)求出小亮与小华第一次相遇时,小华所用的时间以及此时他们离甲地的距离. (2)求出点的坐标及线段所对应的函数关系式;(3)直接写出小华和小亮相距千米时小华骑行的时间. 12.如图1,甲、乙两车分别从相距的、两地相向而行,乙车比甲车先出发小时,并以各自的速度匀速行驶,甲车到达地后因有事立刻按原路原速返回地.乙车从地直达地,两车同时到达地.甲、乙两车距各自出发地的路程(千米)与甲车出发所用的时间(小时)的关系如图,结合图像信息解答下列问题: (1)乙车的速度是 千米/时,乙车行驶 小时到达地; (2)求甲车从地按原路原速返回地的过程中,甲车距它出发地的路程与它出发的时间的函数关系式; (3)求甲车出发多长时间两车相距千米? 13.已知学生公寓、阅览室、超市依次在同一直线上,阅览室离学生公寓1.2,超市离学生公寓2.小明从学生公寓出发,匀速步行了12到阅览室;在阅览室停留70后,匀速步行了10 到超市;在超市停留20后,匀速骑行了8返回学生公寓.给出的图象反映了这个过程中小明离学生公寓的距离y与离开学生公寓的时间x之间的对应关系. 请根据相关信息,解答下列问题: (1)填表: 离开学生公寓的时间/585087112离学生公寓的距离/__________________2
(2)回公寓的路上,小明何时距公寓0.5 ? 14.小明从A地匀速前往B地,同时小亮从B地匀速前往A地,两人离B地的路程与行驶时间之间的函数图像如图所示. (1)A地与B地的距离为 ,小明的速度是 ; (2)求出点P的坐标,并解释其实际意义; (3)设两人之间的距离,在图②中,画出s与x的函数图像(请标出必要的数据); (4)当两人之间的距离小于时,则x的取值范围是 . 15.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费: 第一档是当月用电量不超过240度时实行“基础电价”; 第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费, 超过的部分按照“提高电价”收费.设每个家庭月用电量为x度时,应交电费为y元. 具体收费情况如折线图所示,请根据图象回答下列问题: (1)“基础电价”是____________元度; (2)求出当x>240时,y与x的函数表达式; (3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度? 16.《九章算术》中记载,浮箭漏(图①)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间,某学校STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究: (实验观察)实验小组通过观察,每2小时记录一次箭尺读数,得到下表: 供水时间x(小时)02468箭尺读数y(厘米)618304254
(1)(探索发现): 若以供水时间x为横轴,箭尺读数y为纵轴,建立平面直角坐标系,描出以表格中数据为坐标的各点,试判断这些点是否在同一条直线上.如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,说明理由. (2)(结论应用)应用上述发现的规律估算:供水时间达到12小时时,箭尺的读数为多少厘米? (3)如果本次实验记录的开始时间是上午8:00,那么当箭尺读数为90厘米时是几点钟?
同课章节目录
