4.4用待定系数尝确定一次函数学案(3课时无答案)
文档属性
| 名称 | 4.4用待定系数尝确定一次函数学案(3课时无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 71.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-05 00:00:00 | ||
图片预览


文档简介
4.4用待定系数法确定一次函数
(一)
学习目标:
学会运用待定系数法和数形结合思想求一次函数解析。
体验学习
一、自主探究
阅读教材47、48页的内容,根据所学知识解答例1。
例1:已知一次函数的图像经过点(3,5)和(2,3),求这个一次函数的解析式。
分析:求一次函数y=kx+b的解析式,关键是求出k、b的值,从已知条件可以列出关于k、b的二元一次方程组,并求出k、b。
解:∵一次函数y=kx+b均经过点(3,5)和(2,3)
___________
∴
___________
k=________________
解得:
b=________________
∴一次函数的解析式为_______________
像例1这样先设出函数解析式,再根据已知条件确定解析式中未知数的系数,从而具体写出这个式子的方法,叫做( )
用待定系数法求函数解析式的一般步骤:
1、设出含有待定系数的解析式。
2、把已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程组
3、解方程组,求出待定系数。
4、将求得的待定系数值代入所设的解析式。
二、合作交流:
例2:已知一次函数y=kx+2,当x=5时,y=4。
⑴求这个一次函数。⑵求当x=-2时,函数y的值。
例3:已知一次函数的图像经过两点P(1,3)、Q(2,0),求这个函数的解析式。
三、自主检测:
1、正比例函数y=kx的图像过点(-1,3),则解析式是___________。
2、一次函数y=kx+b的图像过点(1,5)和(0,2),则函数的解析式为___________。
3、若一次函数y=kx-(2k+1)的图像与y轴交于(0,3),则k=___________。
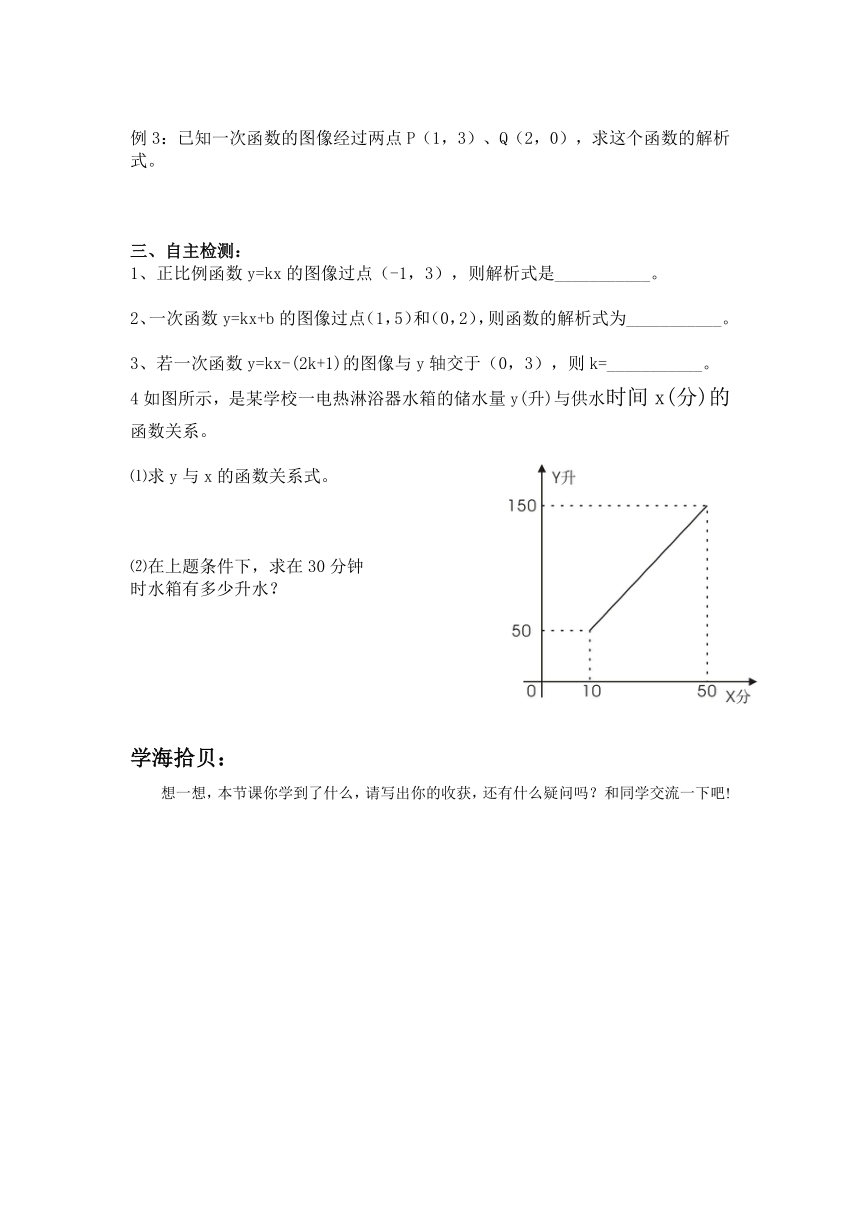
4如图所示,是某学校一电热淋浴器水箱的储水量y(升)与供水时间x(分)的函数关系。
⑴求y与x的函数关系式。
⑵在上题条件下,求在30分钟
时水箱有多少升水?
学海拾贝:
想一想,本节课你学到了什么,请写出你的收获,还有什么疑问吗?和同学交流一下吧!
(二)
学习目标:
在具体情景中,会建立一次函数模型,并会运用所建立的模型进行预测。
体验学习
一、自主探究:
认真阅读50-51页的内容,回答下列问题:
国际奥林匹克运动会早期,男子撑杆跳高的纪录近似地由下表给出:
年份 1900 1904 1908
高度(cm) 3.33 3.53 3.73
1、观察这个表中第二行数据,可以为奥运会的撑杆跳高纪录与时间的关系建立函数模型吗?
2、你能运用这个函数关系式,预测1912年奥运会的撑杆跳高纪录吗?
3、能运用这个函数关系式,预测20世纪8 ( http: / / www.21cnjy.com )0年代,如1988年的奥运会的撑杆跳高纪录吗?为什么预测的1988年奥运会的撑杆跳高纪录高于实际记录?
巩固练习:
小明在练习100m短跑,今年1月至4月份的100m短跑成绩如下表所示:
月份 1 2 3 4
成绩(s) 15.6 15.4 15.2 15
(1)你能为小明的100m短跑成绩与时间的关系建立函数模型吗?
(2)你能用所示求出的函数解析式预测小明今年6月份的100m短跑成绩?
(3)能用所求出的解析是预测小明明年12月份的100m短跑成绩吗?
二、合作交流:
例:已知一次函数的图像如图所示,求它的函数解析式。
例:,某市推出电脑上网包月制,每月收费y(元)与上网时间x(小时)的函数关系如图所示:
(1)、当x≥30时,求y与x之间的函数关系式。
(2)、若小李4月份上网20小时,他应付多少元的上网费用。
(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
自主检测:
1、已知一次函数的图象如图所示,求它的解析式:
2、A(1,4),B(2,m),C(6,-1)在同一条直线上,求m的值。
学海拾贝
与你的同伴交流一下你的收获吧。
(三)
学习目标
1、解关于x的方程kx+b=0可以转化为: ( http: / / www.21cnjy.com )已知函数y=kx+b的函数值为0,求相应的自变量的值。从图像上看,相当于已知直线y=kx+b,确定它与x轴交点的标坐标。
2、在直角坐标系中,以方程kx-y+b=0的解为坐标的点组成的图像就是一次函数y=kx+b的图像。
体验学习
一、探究新知:
例:若直线y=kx+b与两坐标轴所围成的三角形面积是24,求常数k的值是多少?
分析:
⑴一次函数的图像与两条坐标轴围成的图形是直角三角形,两条直角边的长分别是图像与x轴的交点的横坐标的绝对值和与y轴的交点的纵坐标的绝对值。
⑵确定图像与两条坐标的交点坐标可以通过令x=0和y=0解方程求得。
解:
二、合作交流:
例:有一个一次函数的图像,小玲和小芳分别说出了它们两个特征:
小玲:图像与x轴的交点坐标是(6,0)。
小芳:图像与x轴、y轴围成的三角形面积是9。
你知道这个一次函数的关系式吗?
自主检测:
1、直线y=3x+9与x轴的交点坐标是( )
A、(0,-3) B、(-3,0)
C、(0,3) D、(0,-3)
2、直线y=kx+3与x轴的交点是(1,0),则k的值是( )
A、3 B、2 C、-2 D、-3
3、已知直线y=kx+b与直线y=3x-1交于y轴同一点,则b的值是( )
A、1 B、-1 C、 D、-
4、已知直线AB//x轴,且点A的坐标是(-1,1),则直线y=x与直线AB的交点坐标是( )
A、(1,1) B、(-1,-1)
C、(1,-1) D、(-1,1)
5、直线y=3x+6与x轴的交点的横坐标x的值是方程2 x+a=0解,则a的值是________。
6、方程3x+2=8的解是_____,则函数y=3x+2在自变量x 等于____时的函数值等于8。
7、求直线y=2x+8与x轴、y轴的交点坐标,并求与两条坐标轴围成三角形的面积。
学海拾贝:
与同伴谈谈你的心得体会。
(一)
学习目标:
学会运用待定系数法和数形结合思想求一次函数解析。
体验学习
一、自主探究
阅读教材47、48页的内容,根据所学知识解答例1。
例1:已知一次函数的图像经过点(3,5)和(2,3),求这个一次函数的解析式。
分析:求一次函数y=kx+b的解析式,关键是求出k、b的值,从已知条件可以列出关于k、b的二元一次方程组,并求出k、b。
解:∵一次函数y=kx+b均经过点(3,5)和(2,3)
___________
∴
___________
k=________________
解得:
b=________________
∴一次函数的解析式为_______________
像例1这样先设出函数解析式,再根据已知条件确定解析式中未知数的系数,从而具体写出这个式子的方法,叫做( )
用待定系数法求函数解析式的一般步骤:
1、设出含有待定系数的解析式。
2、把已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程组
3、解方程组,求出待定系数。
4、将求得的待定系数值代入所设的解析式。
二、合作交流:
例2:已知一次函数y=kx+2,当x=5时,y=4。
⑴求这个一次函数。⑵求当x=-2时,函数y的值。
例3:已知一次函数的图像经过两点P(1,3)、Q(2,0),求这个函数的解析式。
三、自主检测:
1、正比例函数y=kx的图像过点(-1,3),则解析式是___________。
2、一次函数y=kx+b的图像过点(1,5)和(0,2),则函数的解析式为___________。
3、若一次函数y=kx-(2k+1)的图像与y轴交于(0,3),则k=___________。
4如图所示,是某学校一电热淋浴器水箱的储水量y(升)与供水时间x(分)的函数关系。
⑴求y与x的函数关系式。
⑵在上题条件下,求在30分钟
时水箱有多少升水?
学海拾贝:
想一想,本节课你学到了什么,请写出你的收获,还有什么疑问吗?和同学交流一下吧!
(二)
学习目标:
在具体情景中,会建立一次函数模型,并会运用所建立的模型进行预测。
体验学习
一、自主探究:
认真阅读50-51页的内容,回答下列问题:
国际奥林匹克运动会早期,男子撑杆跳高的纪录近似地由下表给出:
年份 1900 1904 1908
高度(cm) 3.33 3.53 3.73
1、观察这个表中第二行数据,可以为奥运会的撑杆跳高纪录与时间的关系建立函数模型吗?
2、你能运用这个函数关系式,预测1912年奥运会的撑杆跳高纪录吗?
3、能运用这个函数关系式,预测20世纪8 ( http: / / www.21cnjy.com )0年代,如1988年的奥运会的撑杆跳高纪录吗?为什么预测的1988年奥运会的撑杆跳高纪录高于实际记录?
巩固练习:
小明在练习100m短跑,今年1月至4月份的100m短跑成绩如下表所示:
月份 1 2 3 4
成绩(s) 15.6 15.4 15.2 15
(1)你能为小明的100m短跑成绩与时间的关系建立函数模型吗?
(2)你能用所示求出的函数解析式预测小明今年6月份的100m短跑成绩?
(3)能用所求出的解析是预测小明明年12月份的100m短跑成绩吗?
二、合作交流:
例:已知一次函数的图像如图所示,求它的函数解析式。
例:,某市推出电脑上网包月制,每月收费y(元)与上网时间x(小时)的函数关系如图所示:
(1)、当x≥30时,求y与x之间的函数关系式。
(2)、若小李4月份上网20小时,他应付多少元的上网费用。
(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
自主检测:
1、已知一次函数的图象如图所示,求它的解析式:
2、A(1,4),B(2,m),C(6,-1)在同一条直线上,求m的值。
学海拾贝
与你的同伴交流一下你的收获吧。
(三)
学习目标
1、解关于x的方程kx+b=0可以转化为: ( http: / / www.21cnjy.com )已知函数y=kx+b的函数值为0,求相应的自变量的值。从图像上看,相当于已知直线y=kx+b,确定它与x轴交点的标坐标。
2、在直角坐标系中,以方程kx-y+b=0的解为坐标的点组成的图像就是一次函数y=kx+b的图像。
体验学习
一、探究新知:
例:若直线y=kx+b与两坐标轴所围成的三角形面积是24,求常数k的值是多少?
分析:
⑴一次函数的图像与两条坐标轴围成的图形是直角三角形,两条直角边的长分别是图像与x轴的交点的横坐标的绝对值和与y轴的交点的纵坐标的绝对值。
⑵确定图像与两条坐标的交点坐标可以通过令x=0和y=0解方程求得。
解:
二、合作交流:
例:有一个一次函数的图像,小玲和小芳分别说出了它们两个特征:
小玲:图像与x轴的交点坐标是(6,0)。
小芳:图像与x轴、y轴围成的三角形面积是9。
你知道这个一次函数的关系式吗?
自主检测:
1、直线y=3x+9与x轴的交点坐标是( )
A、(0,-3) B、(-3,0)
C、(0,3) D、(0,-3)
2、直线y=kx+3与x轴的交点是(1,0),则k的值是( )
A、3 B、2 C、-2 D、-3
3、已知直线y=kx+b与直线y=3x-1交于y轴同一点,则b的值是( )
A、1 B、-1 C、 D、-
4、已知直线AB//x轴,且点A的坐标是(-1,1),则直线y=x与直线AB的交点坐标是( )
A、(1,1) B、(-1,-1)
C、(1,-1) D、(-1,1)
5、直线y=3x+6与x轴的交点的横坐标x的值是方程2 x+a=0解,则a的值是________。
6、方程3x+2=8的解是_____,则函数y=3x+2在自变量x 等于____时的函数值等于8。
7、求直线y=2x+8与x轴、y轴的交点坐标,并求与两条坐标轴围成三角形的面积。
学海拾贝:
与同伴谈谈你的心得体会。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
