4.1函数和它的表示法学案(2课时无答案)
文档属性
| 名称 | 4.1函数和它的表示法学案(2课时无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 87.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-05 00:00:00 | ||
图片预览

文档简介
4.1函数和它的表示法(一)
教学目标
1、在现实情境中了解变量和函数概念
2、结合实例,了解函数的三种表示方法。
3、知道自变量的取值范围和函数值的意义。
体验学习
一、自主探究:
阅读教材31、32页,并自主探究下列问题:
1、通过阅读三个实例,你能感受到其中所描述的最简单的 变化现象都是在均匀的发生变化?
2、这样的事例在我们的生活中你还能举出几例吗?
3、学生分组讨论分析:
第一个例子中,某地一天中的气温随着时间而变化,从图2-1可看出,凌晨4点的气温是_____℃,下午2点(即14点)的气温是_____℃。
第二个例子中,正方形的面积随着它的边长而变化.
第三个例子中,实用天然气交纳的费用y随所用天然气的体积x而变化,例如当x=10时,y=_____(元),当x=20时,y=_____(元)
4、你能得出什么样的结论:
在讨论问题中,取值会发生变化的量称为_____,取值固定不变的量称为_____。
5、函数的定义(教材32页):
二、合作交流:
阅读教材32和33页的内容,针对32页动脑筋中提出的问题,回答问题
函数的三种表示法是什么?这三种表示法的优点是什么?
三、自主检测:
1、某种商品的单价是每只5元,它的销售额 ( http: / / www.21cnjy.com )y(元)与所售商品数量x(只)之间的关系是_____,其中____是_____的函数,常量是_____。
2、函数y=x2+2x+1中,自变量是_____,其中____是_____的函数。
3、汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(时)的关系为_____。
①当汽车行驶2、3、4、8小时时,计算油箱内有相应的余油量。
②当该车行驶_____小时后油箱内余油量为0升,此时它表示什么?当x=0时,y的值等于_____,此时它表示什么?
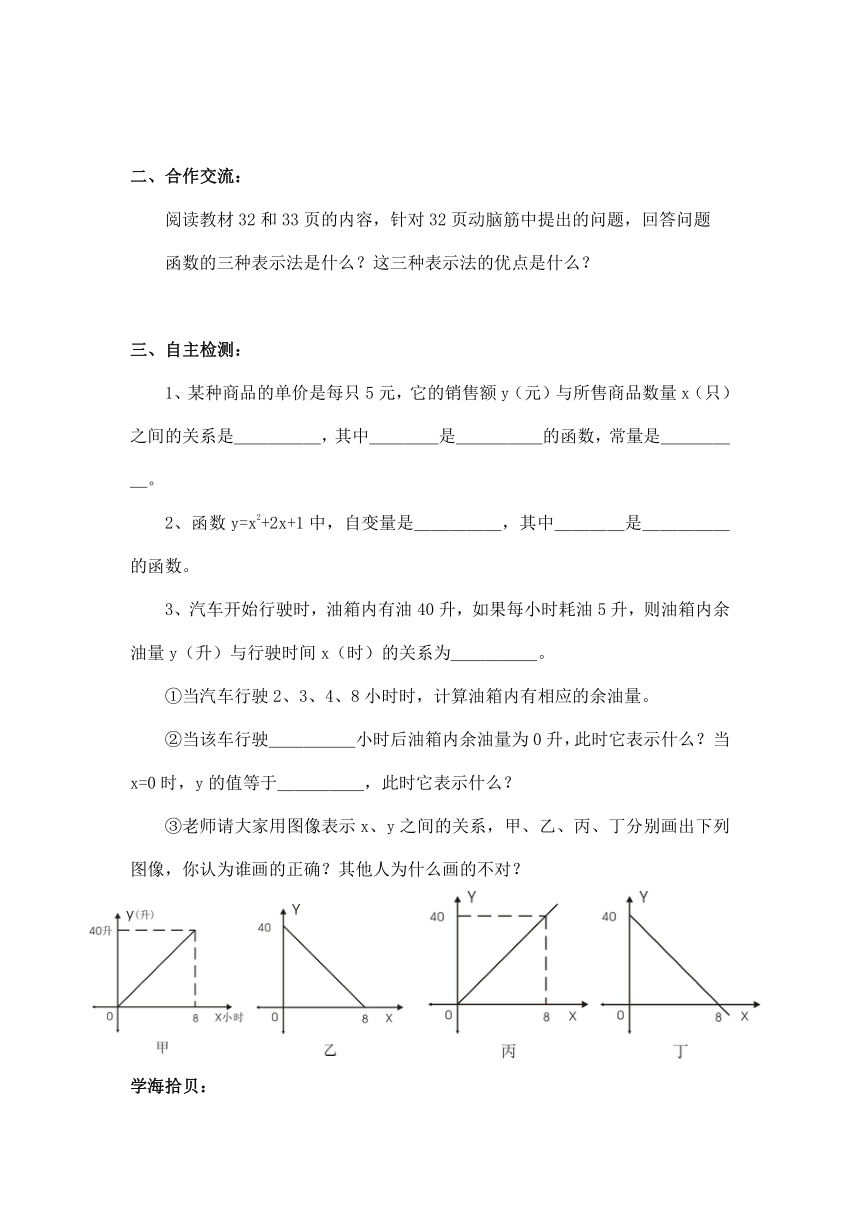
③老师请大家用图像表示x、y之间的关系,甲、乙、丙、丁分别画出下列图像,你认为谁画的正确?其他人为什么画的不对?
学海拾贝:
这节课你有收获吗?与同伴分享你的收获!
4.1函数和它的表示方法(二)
教学目标
1、在现实情景中,会确定函数表达式及自变量的取值范围,会求出函数值。
2、在具体情境中,学会做出函数图像,并会用变量、函数的思想描述数量之间的依存制约关系。
体验学习
一知识链接:
1、函数的三种表示方法是什么?
2、在球的表面积公式S=4πR2中,常量为_____,自变量为____
二、自主探究:
认真阅读教材34页内容,与同伴交流看法,完成下列问题:
用边长为1的等边三角形拼成图形,如图示用y表示拼成的图形的周长,用n表示其中等边三角形的数目,显然拼成的图形周长y是n的函数。
与同伴交流看法。
1、填写下表:
n 1 2 3 4 5 6 7 ……
y
2、你能用公式法表示这个函数关系吗?说一说公式是怎么得出来的?
3、利用此公式,计算1000个这样的等边三角形拼成的图形的周长。
4、你能用图像法表示这个函数关系吗?(画平面直角坐标系,描出相对应的点)。
指导学生观察图像:
①描出的点是y=n+2的图象的一部分,y=n+2的图象是在一条直线上等距离地排列着的一串点。
②它的自变量的取值范围是正整数集。
自变量的取值范围要使自变量的代数式有意义。(如:二次根式的被开方数是非负数,分母不等于0),同时符合实际意义。
三、合作交流:
观察31页图2-1。
观察一天的气温随时间变化的图像与同伴讨论如下问题,发表看法:
(1)哪一段时间里气温在下降,哪一段时间里气温在上升。
(2)这一天最低气温是_____℃,出现在_____时,最高气温是_____℃,出现在_____时。
四、自主检测
1、用长度相同的火柴棒拼成下面由三角形组成的图形。
第n个图形需要的火柴棒的根数y=________________
第n个图形需要的火柴棒的根数y= 。
2、已知卖出糖果数x(kg)与售价y(元)的关系如下表:
X(kg) 1 2 3 4 5
Y(元) 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5
①这个表格反映了哪两个变量之间的关系?它们的关系式是什么?
②你猜想某顾客付了14.7元钱,购买了多少kg的糖果?
学海拾贝:
想一想:本节课你学到了什么?请写出你的收获,还有什么疑问吗?与同伴交流。
教学目标
1、在现实情境中了解变量和函数概念
2、结合实例,了解函数的三种表示方法。
3、知道自变量的取值范围和函数值的意义。
体验学习
一、自主探究:
阅读教材31、32页,并自主探究下列问题:
1、通过阅读三个实例,你能感受到其中所描述的最简单的 变化现象都是在均匀的发生变化?
2、这样的事例在我们的生活中你还能举出几例吗?
3、学生分组讨论分析:
第一个例子中,某地一天中的气温随着时间而变化,从图2-1可看出,凌晨4点的气温是_____℃,下午2点(即14点)的气温是_____℃。
第二个例子中,正方形的面积随着它的边长而变化.
第三个例子中,实用天然气交纳的费用y随所用天然气的体积x而变化,例如当x=10时,y=_____(元),当x=20时,y=_____(元)
4、你能得出什么样的结论:
在讨论问题中,取值会发生变化的量称为_____,取值固定不变的量称为_____。
5、函数的定义(教材32页):
二、合作交流:
阅读教材32和33页的内容,针对32页动脑筋中提出的问题,回答问题
函数的三种表示法是什么?这三种表示法的优点是什么?
三、自主检测:
1、某种商品的单价是每只5元,它的销售额 ( http: / / www.21cnjy.com )y(元)与所售商品数量x(只)之间的关系是_____,其中____是_____的函数,常量是_____。
2、函数y=x2+2x+1中,自变量是_____,其中____是_____的函数。
3、汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(时)的关系为_____。
①当汽车行驶2、3、4、8小时时,计算油箱内有相应的余油量。
②当该车行驶_____小时后油箱内余油量为0升,此时它表示什么?当x=0时,y的值等于_____,此时它表示什么?
③老师请大家用图像表示x、y之间的关系,甲、乙、丙、丁分别画出下列图像,你认为谁画的正确?其他人为什么画的不对?
学海拾贝:
这节课你有收获吗?与同伴分享你的收获!
4.1函数和它的表示方法(二)
教学目标
1、在现实情景中,会确定函数表达式及自变量的取值范围,会求出函数值。
2、在具体情境中,学会做出函数图像,并会用变量、函数的思想描述数量之间的依存制约关系。
体验学习
一知识链接:
1、函数的三种表示方法是什么?
2、在球的表面积公式S=4πR2中,常量为_____,自变量为____
二、自主探究:
认真阅读教材34页内容,与同伴交流看法,完成下列问题:
用边长为1的等边三角形拼成图形,如图示用y表示拼成的图形的周长,用n表示其中等边三角形的数目,显然拼成的图形周长y是n的函数。
与同伴交流看法。
1、填写下表:
n 1 2 3 4 5 6 7 ……
y
2、你能用公式法表示这个函数关系吗?说一说公式是怎么得出来的?
3、利用此公式,计算1000个这样的等边三角形拼成的图形的周长。
4、你能用图像法表示这个函数关系吗?(画平面直角坐标系,描出相对应的点)。
指导学生观察图像:
①描出的点是y=n+2的图象的一部分,y=n+2的图象是在一条直线上等距离地排列着的一串点。
②它的自变量的取值范围是正整数集。
自变量的取值范围要使自变量的代数式有意义。(如:二次根式的被开方数是非负数,分母不等于0),同时符合实际意义。
三、合作交流:
观察31页图2-1。
观察一天的气温随时间变化的图像与同伴讨论如下问题,发表看法:
(1)哪一段时间里气温在下降,哪一段时间里气温在上升。
(2)这一天最低气温是_____℃,出现在_____时,最高气温是_____℃,出现在_____时。
四、自主检测
1、用长度相同的火柴棒拼成下面由三角形组成的图形。
第n个图形需要的火柴棒的根数y=________________
第n个图形需要的火柴棒的根数y= 。
2、已知卖出糖果数x(kg)与售价y(元)的关系如下表:
X(kg) 1 2 3 4 5
Y(元) 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5
①这个表格反映了哪两个变量之间的关系?它们的关系式是什么?
②你猜想某顾客付了14.7元钱,购买了多少kg的糖果?
学海拾贝:
想一想:本节课你学到了什么?请写出你的收获,还有什么疑问吗?与同伴交流。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
