15.2.1平方差公式
图片预览


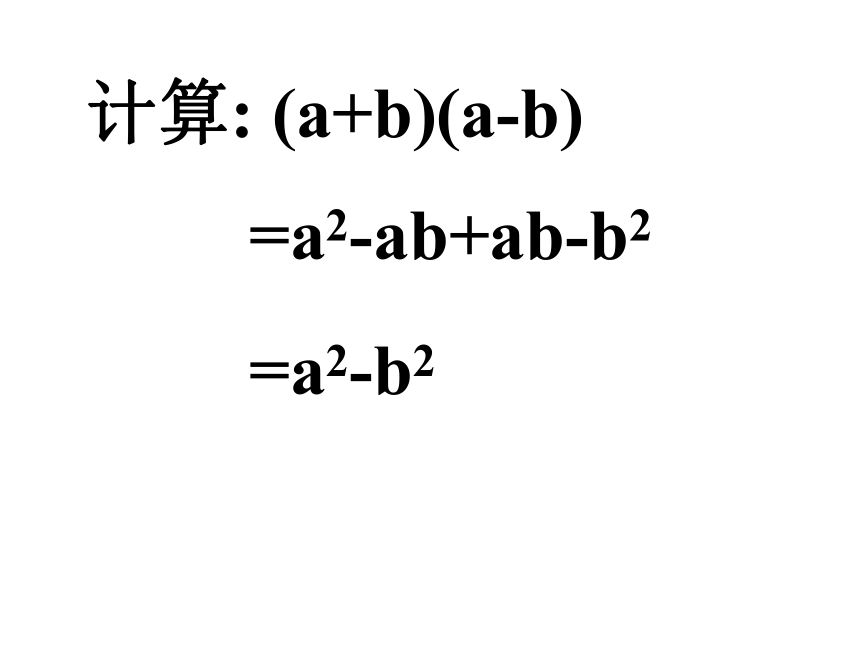





文档简介
课件23张PPT。15.2.2平方差公式计算下列各题:=x2?9 =1?4a2 =x2?16y2 =y2?25z2 观察以上算式及其运算结果,你发现了什么规律?=x2?32 =12?(2a)2 =x2?(4y)2 =y2?(5z)2 .两数和与这两数差的积,等于这两数的平方的差.用式子表示,即:探究:=x2-3x+3x-9=1-2a+2a-4a2=x2-4xy+4xy-16y2=y2-5yz+5yz-25z2?
?
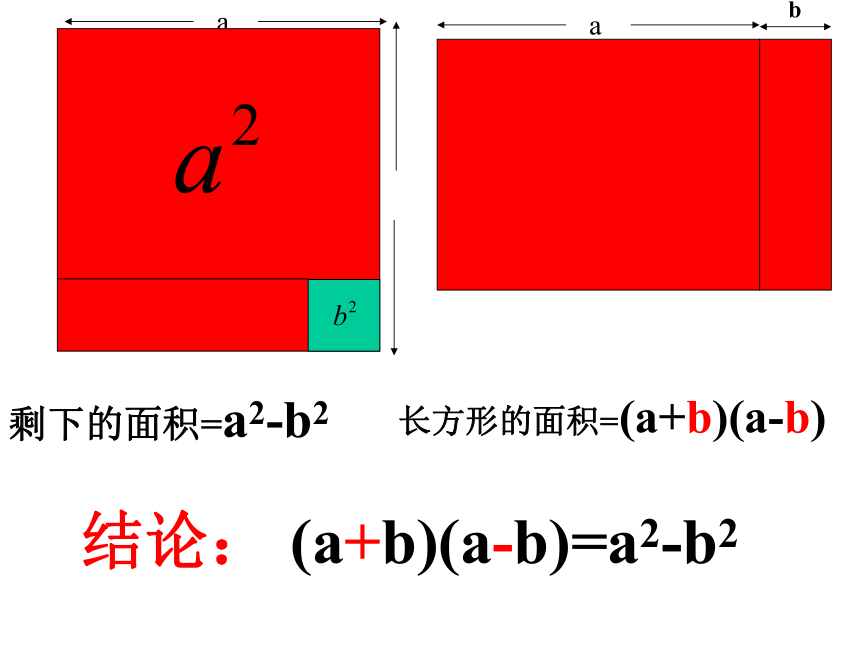
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
a结论: (a+b)(a-b)=a2-b2计算: (a+b)(a-b)=a2-ab+ab-b2=a2-b2平方差公式:(a+b)(a-b)=a2-b2两个数的和与这两个数的差的积等于这两个数的平方差 (1) 公式左边两个二项式必须是相同两数的和与差相乘; 且左边两括号内的第一项相等、第二项符号相反[互为相反数(式)];(2) 公式右边是这两个数的平方差;即右边是左边括号内的第一项的平方减去第二项的平方.
(3) 公式中的a和b 可以代表数,也可以是代数式.
平方差公式:公式的特征是:y3a3b15b-x2填一填:(-2x-3)(2x-3)-32x范例例1、运用平方差公式计算:
(1) (3x+2)(3x-2) (2) (b+2a)(2a-b)
(3)(-x+2y)(-x-2y) 解:(1) (3x+2)(3x-2) =(3x)2-22=9x2-4(2) (b+2a)(2a-b)=(2a)2-b2=(2a+b)(2a-b)=4a2-b2(3) (-x+2y)(-x-2y)=(-x)2-(2y)2=x2-4y2练习:1.下面计算对不对,应怎样改正?
(1)(x+2)(x-2)=x2-2
(2)(-3a-2)(3a-2)=9a2-4
2.运用平方差公式计算:
(1)(a+3b)(a-3b)
(2)(3+2a)(-3+2a)
(3) 51×49
(4)(3x+4)(3x-4)-(2x+3)(3x-2)
(a+b)(a-b)=(a)2-(b)2相反为b 小结 相同为a 适当交换合理加括例2、计算:
(1)102×98 (2)(y+2)(y-2)-(y-1)(y+5) 解:(1) 102×98=(100+2)(100-2)=1002-22=10000-4=9996(2)(y+2)(y-2)-(y-1)(y+5)
=y2 -22-(y2+4y-5)=y2-4-y2-4y+5=-4y+1注:必须符合平方差公式特征的代数式才能用平方差公式例3 计算: (1) a2 (a+b)(a?b)+ a2b2 (2)(2x-5)(2x+5)-2x(2x-3)解:(1)原式= a2( a2-b2)+a2b2=a4-a2b2+a2b2=a4(2)原式=(2 x )2 -25- (4 x 2-6 x )=4 x 2 -25- 4 x 2+6 x =6 x -251. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。两数和与这两数差的积,等于它们的平方差。2.应用平方差公式 时要注意一些什么?运用平方差公式时,要紧扣公式的特征, 找出相等
的“项”和符号相反的“项”,然后应用公式; 变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,要利用加法交换律,3. 对于不符合平方差公式标准形式者,小结运用平方差公式计 算: ① (x+1)(x-1) = ② (m+2)(m-2)= ③ (2x+1)(2x-1) = x2-14x2-1m2-415.3.1 平方差公式④ (x+5y)(x-5y)=x2-25y215.3.1 平方差公式下列计算是否正确?如不正确,应怎样改正?
1.(a-4)(a+4)=a2-4 ( )
2.(2x+5)(2x-5)=2x2-25 ( )
3.(-a-b)(a+b)=a2-b2 ( )
4.(mn-1)(mn+1)=mn2-1 ( )××××运用平方差公式计算:
1.(a+b)(-b+a)=
2.(-a-b)(a-b)=
3.(3a+2b)(3a-2b)=
4.(a5-b2)(a5+b2)=a2-b2b2-a29a2-4b2a10-b4计算:
1.(a-b)(a+b)(a2+b2)
2.(a+b+c)(a+b-c)
=(a2-b2)(a2+b2)=(a2)2-(b2)2=a4-b4=[(a+b)+c][(a+b)-c]=(a+b)2-c2=(a+b)(a+b)-c2=a2+2ab+b2-c2计算:15.3.1 平方差公式20082-2009×2007解:原式=20082-(2008+1)(2008-1)=20082-(20082-1)=20082-20082+1=1推广 !一个长方形的长为 (√19 + √7)厘米,宽为(√19 - √7) 厘米,它的面积是多少?
(√19 + √7)(√19 -√7) =(√19)2- (√7)2(a+b)(a-b)= (a)2-(b)2 2、扩展训练
计算 3982-3992
(2) 在式子(-3a+ )( )的括号内填入怎样的式子才能用平方差公式计算. (3) (1+2)(1+4)(1+22)…(1+2100)(4) (a+b)2-(a-b)2(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y+2x). (不能) 本题是公式的变式训练,以加深对公式本质特征的理解. 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(能) 认真观察:(y-2x)(y+2x)=y2-(2x) 2
=y2-4x2(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2本题对公式的直接运用,以加深对公式本质特征的理解. 指出下列计算中的错误: 第二数被平方时,未添括号。第一 数被平方时,未添括号。第一数与第二数被平方时,
都未添括号。纠 错 练 习
?
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
a结论: (a+b)(a-b)=a2-b2计算: (a+b)(a-b)=a2-ab+ab-b2=a2-b2平方差公式:(a+b)(a-b)=a2-b2两个数的和与这两个数的差的积等于这两个数的平方差 (1) 公式左边两个二项式必须是相同两数的和与差相乘; 且左边两括号内的第一项相等、第二项符号相反[互为相反数(式)];(2) 公式右边是这两个数的平方差;即右边是左边括号内的第一项的平方减去第二项的平方.
(3) 公式中的a和b 可以代表数,也可以是代数式.
平方差公式:公式的特征是:y3a3b15b-x2填一填:(-2x-3)(2x-3)-32x范例例1、运用平方差公式计算:
(1) (3x+2)(3x-2) (2) (b+2a)(2a-b)
(3)(-x+2y)(-x-2y) 解:(1) (3x+2)(3x-2) =(3x)2-22=9x2-4(2) (b+2a)(2a-b)=(2a)2-b2=(2a+b)(2a-b)=4a2-b2(3) (-x+2y)(-x-2y)=(-x)2-(2y)2=x2-4y2练习:1.下面计算对不对,应怎样改正?
(1)(x+2)(x-2)=x2-2
(2)(-3a-2)(3a-2)=9a2-4
2.运用平方差公式计算:
(1)(a+3b)(a-3b)
(2)(3+2a)(-3+2a)
(3) 51×49
(4)(3x+4)(3x-4)-(2x+3)(3x-2)
(a+b)(a-b)=(a)2-(b)2相反为b 小结 相同为a 适当交换合理加括例2、计算:
(1)102×98 (2)(y+2)(y-2)-(y-1)(y+5) 解:(1) 102×98=(100+2)(100-2)=1002-22=10000-4=9996(2)(y+2)(y-2)-(y-1)(y+5)
=y2 -22-(y2+4y-5)=y2-4-y2-4y+5=-4y+1注:必须符合平方差公式特征的代数式才能用平方差公式例3 计算: (1) a2 (a+b)(a?b)+ a2b2 (2)(2x-5)(2x+5)-2x(2x-3)解:(1)原式= a2( a2-b2)+a2b2=a4-a2b2+a2b2=a4(2)原式=(2 x )2 -25- (4 x 2-6 x )=4 x 2 -25- 4 x 2+6 x =6 x -251. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。两数和与这两数差的积,等于它们的平方差。2.应用平方差公式 时要注意一些什么?运用平方差公式时,要紧扣公式的特征, 找出相等
的“项”和符号相反的“项”,然后应用公式; 变成公式标准形式后,再用公式。 或提取两“?”号中的“?”号,要利用加法交换律,3. 对于不符合平方差公式标准形式者,小结运用平方差公式计 算: ① (x+1)(x-1) = ② (m+2)(m-2)= ③ (2x+1)(2x-1) = x2-14x2-1m2-415.3.1 平方差公式④ (x+5y)(x-5y)=x2-25y215.3.1 平方差公式下列计算是否正确?如不正确,应怎样改正?
1.(a-4)(a+4)=a2-4 ( )
2.(2x+5)(2x-5)=2x2-25 ( )
3.(-a-b)(a+b)=a2-b2 ( )
4.(mn-1)(mn+1)=mn2-1 ( )××××运用平方差公式计算:
1.(a+b)(-b+a)=
2.(-a-b)(a-b)=
3.(3a+2b)(3a-2b)=
4.(a5-b2)(a5+b2)=a2-b2b2-a29a2-4b2a10-b4计算:
1.(a-b)(a+b)(a2+b2)
2.(a+b+c)(a+b-c)
=(a2-b2)(a2+b2)=(a2)2-(b2)2=a4-b4=[(a+b)+c][(a+b)-c]=(a+b)2-c2=(a+b)(a+b)-c2=a2+2ab+b2-c2计算:15.3.1 平方差公式20082-2009×2007解:原式=20082-(2008+1)(2008-1)=20082-(20082-1)=20082-20082+1=1推广 !一个长方形的长为 (√19 + √7)厘米,宽为(√19 - √7) 厘米,它的面积是多少?
(√19 + √7)(√19 -√7) =(√19)2- (√7)2(a+b)(a-b)= (a)2-(b)2 2、扩展训练
计算 3982-3992
(2) 在式子(-3a+ )( )的括号内填入怎样的式子才能用平方差公式计算. (3) (1+2)(1+4)(1+22)…(1+2100)(4) (a+b)2-(a-b)2(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y+2x). (不能) 本题是公式的变式训练,以加深对公式本质特征的理解. 下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (第一个数不完全一样 ) (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(能) 认真观察:(y-2x)(y+2x)=y2-(2x) 2
=y2-4x2(1) (1+2x)(1?2x)=1?2x2
(2) (2a2+b2)(2a2?b2)=2a4?b4
(3) (3m+2n)(3m?2n)=3m2?2n2本题对公式的直接运用,以加深对公式本质特征的理解. 指出下列计算中的错误: 第二数被平方时,未添括号。第一 数被平方时,未添括号。第一数与第二数被平方时,
都未添括号。纠 错 练 习
