2.2乘法公式学案(4课时无答案)
图片预览



文档简介
2.2乘法公式
2.2.1平方差公式
学习目标:
1.经历探索平方差公式的过程.
2.会推导平方差公式,并能运用公式进行简单的运算
重 点: 平方差公式的推导和应用
难 点: 理解平方差公式的结构特征,灵活应用平方差公式.
预习导学——不看不讲
学一学:阅读教材P42“动脑筋”与“说一说”
说一说:计算下列多项式的积.
(1)(x+1)(x-1)
(2)(m+2)(m-2)
(3)(2x+1)(2x-1)
(4)(x+5y)(x-5y)
议一议:观察上述算式,你发现什么规律?运算出结果后,你又发现什么规律?再举两例验证你的发现.
【归纳总结】
两个数的和与这两个数的差的积,等于这两个数的平方差.
即:(a+b)(a-b)=a2-b2
你能用数形结合的思想解释平方差公式吗?
想一想:下列各式计算对不对?若不对应怎样改正?
(1)(x+2)(x-2)=x2-2 (2)(-3a-2)(3a-2)=9a2-4
填一填:
(a+b)(-b+a) = (3a+2b)(3a-2b)=
公式的结构特征
公式的字母a、b可以表示数,也可以表示单项式、多项式;
②要符合公式的结构特征才能运用平方差公式;
③有些式子表面上不能应用公式,但通过适当变形实质上能应用公式.
如:(x+y-z)(x-y-z)=[(x-z)+y][(x-z)-y]=(x-z)2-y2.
【课堂展示】P43例题1,2,3
合作探究——不议不讲
互动探究一:运用乘法公式计算:7×8
互动探究二:下列哪些多项式相乘可以用平方差公式?
【当堂检测】:
1.填空
(1) (__+__)(__+__)=
(2) (a+2b+2c)(a+2b-2c)写成平方差公式形式:
2.计算
(1)102×98
(2)(a+b)(a-b)(a2+b2)
(3)(y+2)(y-2)-(y-1)(y+5)
(4)(b+2a)(2a-b)
(5)(-x+2y)(-x-2y)
(6)(a+2b+2c)(a+2b-2c)
2.2.2 完全平方公式(1)
学习目标:
1.会推导完全平方公式:,了解公式的几何解释,并能运用公式计算。
2.经历探索完全平方公式的推导过程,发展符号感,体会“特殊----一般----特殊”的认识规律。
重点:掌握公式的结构特征和字母表示的广泛含义,正确运用公式进行计算.
难点:运用完全平方公式进行计算.
预习导学——不看不讲
学一学:阅读教材P44“动脑筋”与“做一做”
说一说:计算 两名学生板演,其他学生在练习本上完成,然后说出答案,得出公式.
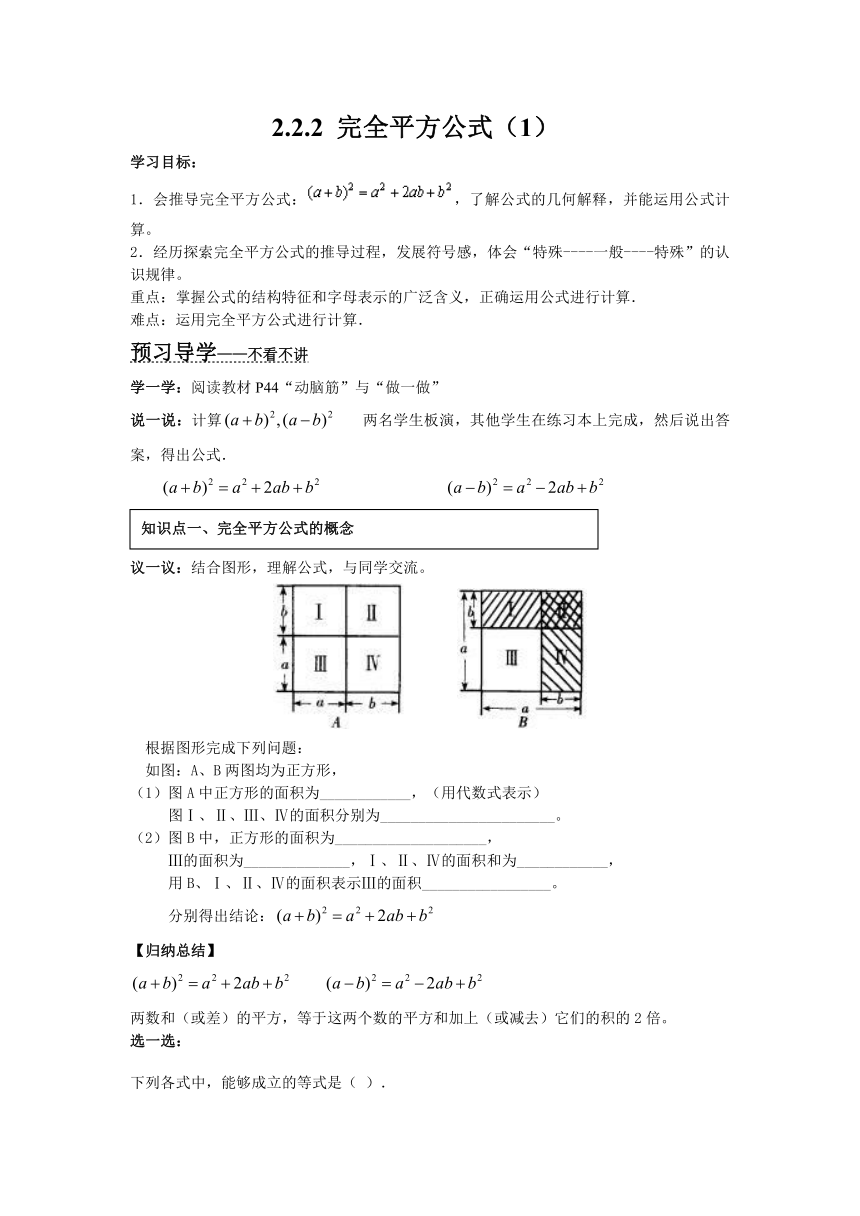
议一议:结合图形,理解公式,与同学交流。
根据图形完成下列问题:
如图:A、B两图均为正方形,
(1)图A中正方形的面积为____________,(用代数式表示)
图Ⅰ、Ⅱ、Ⅲ、Ⅳ的面积分别为_______________________。
(2)图B中,正方形的面积为____________________,
Ⅲ的面积为______________,Ⅰ、Ⅱ、Ⅳ的面积和为____________,
用B、Ⅰ、Ⅱ、Ⅳ的面积表示Ⅲ的面积_________________。
分别得出结论:
【归纳总结】
两数和(或差)的平方,等于这两个数的平方和加上(或减去)它们的积的2倍。
选一选:
下列各式中,能够成立的等式是( ).
A、 B、
C、 D、
填一填:(1) )2=
是一个完全平方式,则m的值是___________
说说完全平方公式的特征,和你的伙伴交流认识
【课堂展示】 引例:计算
讲解:在 中,把x看成a,把2y看成b,在 中把2x看成a,把-3y看成b,则 、 ,就可用完全平方公式来计算,即
(a + b)2 =a2+ 2 a b + b2
合作探究——不议不讲
互动探究一:P45例题4
互动探究二:下面各式计算对不对?应怎样改正?
(1) (2)
【当堂检测】:
1.运用完全平方公式计算:
(1)(m-n) (3)
⑶ 1999 (4)( a-3b)(3b-a)
2.2.2 完全平方公式(2)
学习目标:
1、熟练应用完全平方公式、平方差公式计算。
2、进一步发展学生的符号感,体会“特殊----一般----特殊”的认识规律。
重点:掌握公式的结构特征和字母表示的广泛含义,正确运用公式进行计算.
难点:运用完全平方公式、平方差公式进行计算.
预习导学——不看不讲
说一说:1.叙述完全平方公式的内容并用字母表示:
2. 与 , 与 相等吗?
【归纳总结】
运用完全平方公式计算时,要注意:
(1)切勿把此公式与公式 混淆,而随意写成 .
(2)切勿把“乘积项”2ab中的2丢掉.
(3)计算时,要先观察题目是否符合公式的 ( http: / / www.21cnjy.com )条件.若不符合,应先变形为符合公式的条件的形式,再利用公式进行计算;若不能变为符合条件的形式,则应运用乘法法则进行计算.要想用好公式,关键在于辨认题目的结构特征,
选一选:判断下列运算正确的是.
(1)2a-b-=2a-(b-) (2)m-3n+2a-b=m+(3n+2a-b)
(3)2x-3y+2=-(2x+3y-2) (4)a-2b-4c+5=(a-2b)-(4c+5)
【课堂展示】例:如果,那么的结果是多少?
合作探究——不议不讲
互动探究一:P46例题5
互动探究二: P47例题6 计算
(1) (2)
(3)
得出结论:
①两数之和的平方与两数之差的平方相差
两数之和的平方与两数之差的平方相加得
③三个数之和的完全平方公式
互动探究三: P47例题7
【当堂检测】:
1.填空
(1) 计算:152= 252= 352= 452=
(2)总结归纳有何规律
(3) 已知(x+y)2=9,(x-y)2=5,则xy=
(4)(a+b)2 = (a-b)2+ ________.
(5)若x+y=3,x-y=1,则x2+ y2 = , xy = .
2.计算
(1) (2)
3.已知,求的值
4.如果是一个完全平方公式,则的值是多少?
2.2.3运用乘法公式进行计算
学习目标:
1、学习型,并进行公式推导;
2、进一步巩固完全平方公式和平方差公式,并会用乘法公式化简某些代数式;
重点:乘法公式的有关推广计算.
预习导学——不看不讲
学一学:阅读教材P48“动脑筋”
说一说: 平方差公式与完全平方公式及其结构特征
(1)
议一议:计算下列各题
(1) (2)
【归纳总结】遇到多项式的乘法时,要先观察式子的特征,看能否运用乘法公式,一达到简化运算的目的。
选一选:下列多项式的乘法中可用平方差公式计算的是( ).
A. B. C. D.
填一填:-2ab =
你能用推导的结果吗?
【课堂展示】例8 运用乘法公式计算
(1) (2)
合作探究——不议不讲
互动探究一:是完全平方式,则m的若要使值为( ).
A. B. C. D.
互动探究二:若求(1) (2)的值.
互动探究二:计算:[2a2-(a+b)(a-b)][(-a-b)(-a+b)+2b2];
【当堂检测】:
1.填空
(1)、;
(2)、;
(3)、;
2.计算
(1)
(2)
(3)
(4)
3. 思考:你能计算、吗?
4. 已知 ,求和 的值
知识点一、平方差公式的概念
知识点二、平方差公式的运用
知识点一、完全平方公式的概念
知识点二、 完全平方公式 的运用
知识点一、完全平方公式 的结构特征
知识点二、 完全平方公式 的运用
知识点一、 平方差公式与完全平方公式 的概念
知识点二、乘法公式的运用
2.2.1平方差公式
学习目标:
1.经历探索平方差公式的过程.
2.会推导平方差公式,并能运用公式进行简单的运算
重 点: 平方差公式的推导和应用
难 点: 理解平方差公式的结构特征,灵活应用平方差公式.
预习导学——不看不讲
学一学:阅读教材P42“动脑筋”与“说一说”
说一说:计算下列多项式的积.
(1)(x+1)(x-1)
(2)(m+2)(m-2)
(3)(2x+1)(2x-1)
(4)(x+5y)(x-5y)
议一议:观察上述算式,你发现什么规律?运算出结果后,你又发现什么规律?再举两例验证你的发现.
【归纳总结】
两个数的和与这两个数的差的积,等于这两个数的平方差.
即:(a+b)(a-b)=a2-b2
你能用数形结合的思想解释平方差公式吗?
想一想:下列各式计算对不对?若不对应怎样改正?
(1)(x+2)(x-2)=x2-2 (2)(-3a-2)(3a-2)=9a2-4
填一填:
(a+b)(-b+a) = (3a+2b)(3a-2b)=
公式的结构特征
公式的字母a、b可以表示数,也可以表示单项式、多项式;
②要符合公式的结构特征才能运用平方差公式;
③有些式子表面上不能应用公式,但通过适当变形实质上能应用公式.
如:(x+y-z)(x-y-z)=[(x-z)+y][(x-z)-y]=(x-z)2-y2.
【课堂展示】P43例题1,2,3
合作探究——不议不讲
互动探究一:运用乘法公式计算:7×8
互动探究二:下列哪些多项式相乘可以用平方差公式?
【当堂检测】:
1.填空
(1) (__+__)(__+__)=
(2) (a+2b+2c)(a+2b-2c)写成平方差公式形式:
2.计算
(1)102×98
(2)(a+b)(a-b)(a2+b2)
(3)(y+2)(y-2)-(y-1)(y+5)
(4)(b+2a)(2a-b)
(5)(-x+2y)(-x-2y)
(6)(a+2b+2c)(a+2b-2c)
2.2.2 完全平方公式(1)
学习目标:
1.会推导完全平方公式:,了解公式的几何解释,并能运用公式计算。
2.经历探索完全平方公式的推导过程,发展符号感,体会“特殊----一般----特殊”的认识规律。
重点:掌握公式的结构特征和字母表示的广泛含义,正确运用公式进行计算.
难点:运用完全平方公式进行计算.
预习导学——不看不讲
学一学:阅读教材P44“动脑筋”与“做一做”
说一说:计算 两名学生板演,其他学生在练习本上完成,然后说出答案,得出公式.
议一议:结合图形,理解公式,与同学交流。
根据图形完成下列问题:
如图:A、B两图均为正方形,
(1)图A中正方形的面积为____________,(用代数式表示)
图Ⅰ、Ⅱ、Ⅲ、Ⅳ的面积分别为_______________________。
(2)图B中,正方形的面积为____________________,
Ⅲ的面积为______________,Ⅰ、Ⅱ、Ⅳ的面积和为____________,
用B、Ⅰ、Ⅱ、Ⅳ的面积表示Ⅲ的面积_________________。
分别得出结论:
【归纳总结】
两数和(或差)的平方,等于这两个数的平方和加上(或减去)它们的积的2倍。
选一选:
下列各式中,能够成立的等式是( ).
A、 B、
C、 D、
填一填:(1) )2=
是一个完全平方式,则m的值是___________
说说完全平方公式的特征,和你的伙伴交流认识
【课堂展示】 引例:计算
讲解:在 中,把x看成a,把2y看成b,在 中把2x看成a,把-3y看成b,则 、 ,就可用完全平方公式来计算,即
(a + b)2 =a2+ 2 a b + b2
合作探究——不议不讲
互动探究一:P45例题4
互动探究二:下面各式计算对不对?应怎样改正?
(1) (2)
【当堂检测】:
1.运用完全平方公式计算:
(1)(m-n) (3)
⑶ 1999 (4)( a-3b)(3b-a)
2.2.2 完全平方公式(2)
学习目标:
1、熟练应用完全平方公式、平方差公式计算。
2、进一步发展学生的符号感,体会“特殊----一般----特殊”的认识规律。
重点:掌握公式的结构特征和字母表示的广泛含义,正确运用公式进行计算.
难点:运用完全平方公式、平方差公式进行计算.
预习导学——不看不讲
说一说:1.叙述完全平方公式的内容并用字母表示:
2. 与 , 与 相等吗?
【归纳总结】
运用完全平方公式计算时,要注意:
(1)切勿把此公式与公式 混淆,而随意写成 .
(2)切勿把“乘积项”2ab中的2丢掉.
(3)计算时,要先观察题目是否符合公式的 ( http: / / www.21cnjy.com )条件.若不符合,应先变形为符合公式的条件的形式,再利用公式进行计算;若不能变为符合条件的形式,则应运用乘法法则进行计算.要想用好公式,关键在于辨认题目的结构特征,
选一选:判断下列运算正确的是.
(1)2a-b-=2a-(b-) (2)m-3n+2a-b=m+(3n+2a-b)
(3)2x-3y+2=-(2x+3y-2) (4)a-2b-4c+5=(a-2b)-(4c+5)
【课堂展示】例:如果,那么的结果是多少?
合作探究——不议不讲
互动探究一:P46例题5
互动探究二: P47例题6 计算
(1) (2)
(3)
得出结论:
①两数之和的平方与两数之差的平方相差
两数之和的平方与两数之差的平方相加得
③三个数之和的完全平方公式
互动探究三: P47例题7
【当堂检测】:
1.填空
(1) 计算:152= 252= 352= 452=
(2)总结归纳有何规律
(3) 已知(x+y)2=9,(x-y)2=5,则xy=
(4)(a+b)2 = (a-b)2+ ________.
(5)若x+y=3,x-y=1,则x2+ y2 = , xy = .
2.计算
(1) (2)
3.已知,求的值
4.如果是一个完全平方公式,则的值是多少?
2.2.3运用乘法公式进行计算
学习目标:
1、学习型,并进行公式推导;
2、进一步巩固完全平方公式和平方差公式,并会用乘法公式化简某些代数式;
重点:乘法公式的有关推广计算.
预习导学——不看不讲
学一学:阅读教材P48“动脑筋”
说一说: 平方差公式与完全平方公式及其结构特征
(1)
议一议:计算下列各题
(1) (2)
【归纳总结】遇到多项式的乘法时,要先观察式子的特征,看能否运用乘法公式,一达到简化运算的目的。
选一选:下列多项式的乘法中可用平方差公式计算的是( ).
A. B. C. D.
填一填:-2ab =
你能用推导的结果吗?
【课堂展示】例8 运用乘法公式计算
(1) (2)
合作探究——不议不讲
互动探究一:是完全平方式,则m的若要使值为( ).
A. B. C. D.
互动探究二:若求(1) (2)的值.
互动探究二:计算:[2a2-(a+b)(a-b)][(-a-b)(-a+b)+2b2];
【当堂检测】:
1.填空
(1)、;
(2)、;
(3)、;
2.计算
(1)
(2)
(3)
(4)
3. 思考:你能计算、吗?
4. 已知 ,求和 的值
知识点一、平方差公式的概念
知识点二、平方差公式的运用
知识点一、完全平方公式的概念
知识点二、 完全平方公式 的运用
知识点一、完全平方公式 的结构特征
知识点二、 完全平方公式 的运用
知识点一、 平方差公式与完全平方公式 的概念
知识点二、乘法公式的运用
