2015年中考数学二轮专题复习教案:专题10 图形的计算与证明
文档属性
| 名称 | 2015年中考数学二轮专题复习教案:专题10 图形的计算与证明 |  | |
| 格式 | zip | ||
| 文件大小 | 90.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-05 08:54:19 | ||
图片预览




文档简介
备战2015年中考二轮讲练测
第一篇 专题整合篇
专题10 (讲案)
一讲考点——考点梳理
(一)三角形中的特殊线段
1.三角形的角平分线
(1)概念:三角形的一个角的平分线,与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
(2)三角形的三条角平分线都在三角形的内部,且交于一点,交点叫三角形的内心,内心到_____________的距离相等.
2.三角形的中线.
(1)概念:在三角形中,连接一个顶点和它所对的边的中点的线段叫做三角形的中线.
(2)三角形的三条中线都在三角形的内部,且交于一点,交点叫三角形的中心,重心把中线分为1:2两部分(到顶点的距离占2份).
3.三角形的高线
(1)概念:从三角形的一个顶点向它的对边所在直线画垂直线,顶点和垂足间的线段叫做三角形的高线.
(2)三角形的三条高或高的延长线交于一点 ( http: / / www.21cnjy.com ),交点叫做三角形的垂心.锐角三角形垂心在三角形的内部,直角三角形的垂心即直角三角形的直角顶点,钝角三角形的垂心在三角形的外部.
4.三角形的中位线
(1)概念:连接三角形两边中点的线段叫做三角形的中位线.
(2)三角形的三条中位线都在三角形的内部,三角形的中位线平行于_____________,且_____________
(二)三角形的性质
1.三角形的三边关系
三角形任意两边之和大于第三边,任意两边之差小于第三边.
判断三条线段是否能组成三角形时,只需要判断较短的两条线段长之和是否大于第三遍即可.
2.三角形的角
(1)三角形的三个内角之和为_____________.
(2)三角形的外角:三角形的一个外角等于_____________ ;三角形的一个外角大于与它不相邻的任何一个内角.
(3)三角形的外角和为________.
(三)全等三角形的判定条件
(1)边角边(SAS):有两边及其夹角对应相等的两个三角形全等.
(2)角边角(ASA):有两角及其夹边对应相等的两个三角形全等.
(3)角角边(AAS):有两角及其一角的对边对应相等的两个三角形全等.
(4)边边边(SSS):三边对应相等的两个三角形全等.
(5)斜边、直角边(HL)(适用于直角三角形):斜边及一直角边对应相等的两个直角三角形全等.
(四)等腰三角形与等边三角形
一、等腰三角形
1.等腰三角形的概念
有两条边相等的三角形,叫做等腰三角形,相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
特别的,三条边都相等的三角形叫做等边三角形.
2等腰三角形的性质
(1)等腰三角形的两个底角相等.
(2)等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.
(3)等腰三角形是轴对称图形.
3.等腰、等边三角形的判定
(1)_____________.
(2)三个内角都相等的三角形是等边三角形.
(3)有_____________的等腰三角形是等边三角形.
(五)角平分线与线段的垂直平分线
1. 角平分线
(1)角平分线的性质:角平分线上的点_____________.
(2)角平分线的判定:到角两边距离相等的点在该角的平分线上.
2. 线段的垂直平分线
(1)概念:经过线段中点,并且垂直于这条线段的直线叫做这条线段的垂直平分线,也叫中垂线.
(2)线段垂直平分线上的点到_____________ 相等.到一条线段的两个端点距离相等的点在这条线段的垂直平分线上.
(六)平行四边形
1.平行四边形的概念与性质:两组对边分别平行的四边形叫做平行四边形.
平行四边形的性质:
平行四边形具有四边形的所有性质.
平行四边形的两组对边分别_____________.
平行四边形的两组对角分别相等,邻角互补.
平行四边形的对角线_____________.
平行四边形是中心对称图形,对称中心是对角线的交点.
2.平行四边形的判定
(1). _____________的四边形是平行四边形.
(2). _____________的四边形是平行四边形.
(3). _____________的四边形是平行四边形.
(4). _____________的四边形是平行四边形.
(5). _____________的四边形是平行四边形.
(七)矩形、菱形
1.矩形
(1).矩形的定义有一个角是直角的平行四边形叫做矩形.
(2).矩形的性质:
①矩形具有平行四边形的一切性质.
②矩形的四个角都是直角.
③矩形的对角线_____________.
(3).矩形的判定定理
①有三个角是直角的四边形是矩形.
②_____________ 是矩形.
③_____________是矩形.
④对角线相等且互相平分的四边形是矩形.
2.菱形
(1)菱形的定义:有一组邻边相等的平行四边形是菱形.
(2)菱形的性质:
①四条边都相等;
②菱形的对角线_____________,并且每一条对角线_____________.
(3)菱形的判定
①________________________是菱形
②__________________________是菱形
③四边相等的四边形是菱形
(八)圆的有关性质及计算
1.垂径定理及其推论
垂径定理:垂直于弦的直径_____________,并且平分_____________.
推论1:①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
②弦的垂直平分线经过圆心角,并且平分弦所对的两条弧;
③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
推论2:圆的两条平行弦所夹的弧______.
2、圆心角、弧、弦和弦心距之间的关系
(1).在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
(2).在同圆或等圆中,如果两个圆心角、两条弦、两条弧或两条两条弦的弦心距中有一组量相等,那么其余的各组量也都分别相等.
3.圆周角定理及其推论
(1)在同圆或等圆中,同弧或等弧所对的圆周 ( http: / / www.21cnjy.com )角_____,都等于它所对的圆心角_____________,这些可以作为证明角相等和角度计算的依据.
(2)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.应用时,常常需要添加辅助线,构成直径所对的圆周角.
4.弧长、扇形的面积
(1).如果弧长为l,圆心角为n°,圆的半径为r,那么弧长的计算公式为_____________
(2).由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
若扇形的圆心角为n°,所在圆的半径为r,弧长为l,面积为S,则_____________
5、圆柱和圆锥
(1).圆柱的侧面积圆柱的侧面展开图为一矩形,矩形的宽为圆柱的高,矩形的长为圆柱的底面圆的周长.
圆柱的侧面积:若圆柱的高为l,底面半径为r,则 =2πrl.
(2).圆锥的侧面积、全面积的计算
圆锥的侧面展开图是以圆锥母线为半径,圆锥底面圆的周长为弧长的扇形.
圆锥的侧面积:圆锥的侧面积是指圆锥侧面展开图的面积,=πrl.
二讲题型——题型解析
(一)全等三角形的性质与判定
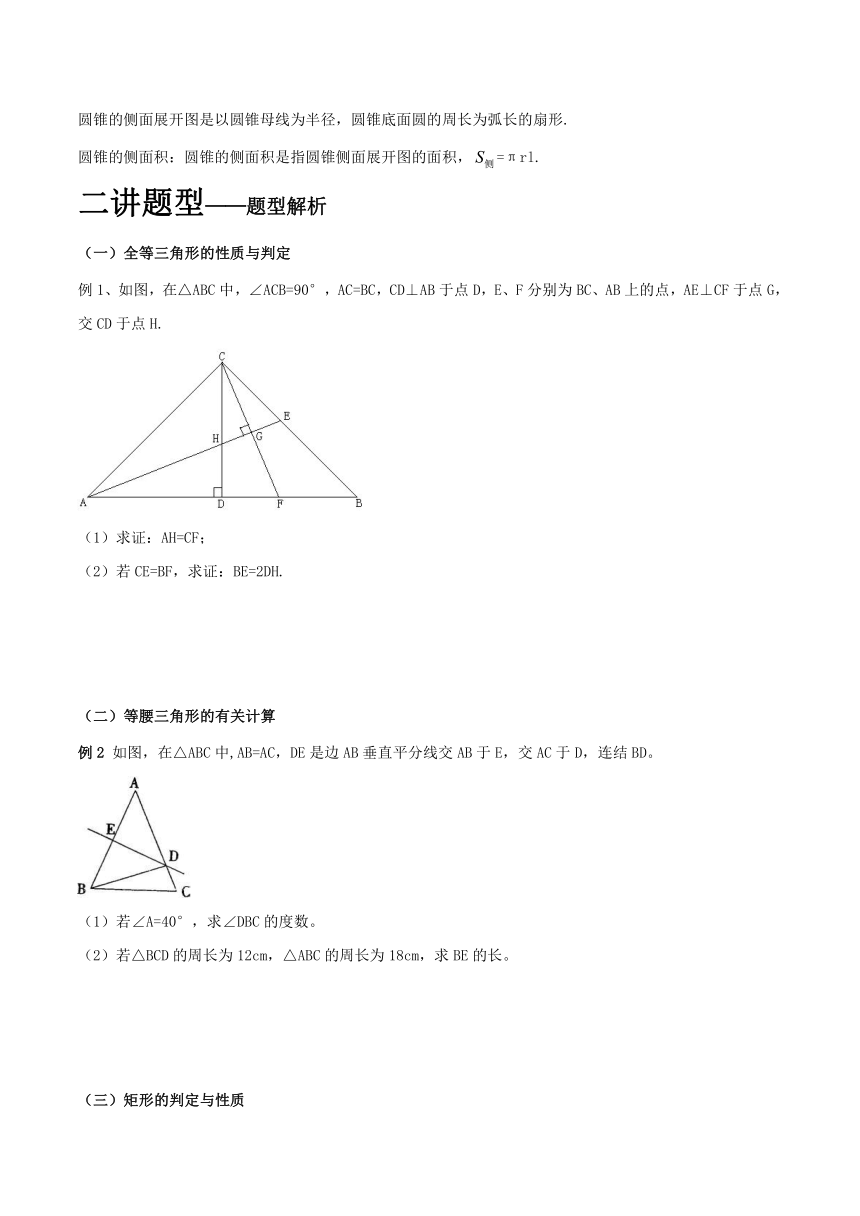
例1、如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,E、F分别为BC、AB上的点,AE⊥CF于点G,交CD于点H.
( http: / / www.21cnjy.com )
(1)求证:AH=CF;
(2)若CE=BF,求证:BE=2DH.
(二)等腰三角形的有关计算
例2 如图,在△ABC中,AB=AC,DE是边AB垂直平分线交AB于E,交AC于D,连结BD。
( http: / / www.21cnjy.com )
(1)若∠A=40°,求∠DBC的度数。
(2)若△BCD的周长为12cm,△ABC的周长为18cm,求BE的长。
(三)矩形的判定与性质
例3、如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)求证:BE=DE.
(2)若四边形ABCD的面积为9,求BE的长
(四) 圆的切线的有关计算与证明
例4如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
( http: / / www.21cnjy.com )
(1)求证:AD⊥DC;
(2)若AD=2,AC=,求AB的长.
(五)平行四边形的有关计算与证明
例5 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
( http: / / www.21cnjy.com )
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD= MN.
(六)菱形的性质与证明
例6已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
( http: / / www.21cnjy.com )
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
(七)圆的有关性质与计算
例7如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
( http: / / www.21cnjy.com )
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
三讲方法——方法点睛
(一)证明角或线段的关系:在几何证明与计算 ( http: / / www.21cnjy.com )过程中,若看到边、角的证明,优先考虑证明三角形全等,若告诉两组对应边相等,则优先考虑利用“SAS”找出夹角证明三角形全等;若告诉两组对应角相等,则可以考虑“ASA”、“AAS”;同时,在证明直角三角形全等时,在找角相等,通常利用“同角的余角相等”.
(二)对于一般三角形中的计 ( http: / / www.21cnjy.com )算问题,常用到其性质:三边关系:三角形的两边之和大于第三边,两边之差小于第三边;内角和定理:三角形的内角和等于180°;外角的性质:三角形的一个外角等于与它不相邻的两个内角的和;边角关系:在同一个三角形中,大边对大角,小边对小角.
(三)在平行四边形中若求线段的比,首先 ( http: / / www.21cnjy.com )利用平行四边形的性质,找相似三角形的比例式,找出与要求线段的比有关的比例关系,再利用线段的等量代换求解即可.
(四)在菱形中,若存在一个角为60°,则连接另外两点的对角线所分割的两个三角形为等边三角形,故在计算时,利用等边三角形的性质进行计算.
(五)在菱形的证明过程中,若已知四边形是平行四边形,则只需要证一组邻边相等或对角线互相垂直即可;若相等的边较多,则只需证四条边相等即可.
(六)在利用垂径定理求线段时,通常 ( http: / / www.21cnjy.com )连接半径,作弦心距,利用勾股定理来解答,同时注意半径、弦长的一半、弦心距构成直角三角形,利用勾股定理可以对圆的半径、弦长、弦心距“知二求一”.
(七)在圆的切线证明时,若已知直线 ( http: / / www.21cnjy.com )与圆有公共点,则连接过这点的半径,证明这条半径与直线垂直即可,简记为:有切点,连半径,证垂直;若未知直线与圆有公共点,则过圆心作直线的垂线段,证明垂线段的长等于半径,可简记为:无切点,作垂直,证半径.
(八)阴影部分面积的求法:
①公式法:针对规则的扇形,直接利用公式进行计算即可;
②割补法:针对不规则的图形,可将不规则的图形经过平移或分割转化为几个规则的图形,进行面积的和或差的计算;
③等积变换法:针对不规则的图形,将不规则的图形拼凑成等积的规则图形求解.
四练实题——随堂小练
1. 如图,在矩形ABCD中,AB=3,BC=4,将其折叠,使AB边落在对角线AC上,得到折痕AE,则点E到点B的距离为
( http: / / www.21cnjy.com )
A. B.2 C. D. 3
2. 如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )
( http: / / www.21cnjy.com )
A. B. C. D.
3. 如图,在中,,过顶点的直线,、的平分线分别交于点、,若,,则的长为 .
( http: / / www.21cnjy.com )
4. 如图边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为,,则的值为 .
( http: / / www.21cnjy.com )
5. 如图,矩形ABCD的对角线AC、BD相 ( http: / / www.21cnjy.com )交于点O,DE∥AC,CE∥BD,若AC=4,则四边形CODE的周长为
( http: / / www.21cnjy.com )
6. 如图,点P是菱形ABCD的对角线BD上一点,连结AP、CP,延长CP交AD于E,交BA的延长线于F.
( http: / / www.21cnjy.com )
(1)求证:∠DCP=∠DAP;
(2)若AB=2,DP:PB=1:2,且PA⊥BF,求对角线BD的长.
五练原创——预测提升
1.如图,AB是⊙O的直径,C.D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠BOC=( )
( http: / / www.21cnjy.com )
A.25° B.50° C.130° D.155°
2. 如图,在△ABC中, ( http: / / www.21cnjy.com )边AB的垂直平分线分别交BC于点D,交AB于点E.若AE=3,△ADC的周长为8,则△ABC的周长为 .
( http: / / www.21cnjy.com )
3. 将正方形ABCD中的△ABP绕点B顺时针旋转能与△CBP′重合,若BP=4,则PP′= _________ .
( http: / / www.21cnjy.com )
5. 如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作 ABDE,连接AD,EC.
( http: / / www.21cnjy.com )
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
6. 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
( http: / / www.21cnjy.com )
(1)求证:DE与⊙O相切;
(2)连结AD,己知BC=10,BE=2,求sin∠BAD的值.
第一篇 专题整合篇
专题10 (讲案)
一讲考点——考点梳理
(一)三角形中的特殊线段
1.三角形的角平分线
(1)概念:三角形的一个角的平分线,与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
(2)三角形的三条角平分线都在三角形的内部,且交于一点,交点叫三角形的内心,内心到_____________的距离相等.
2.三角形的中线.
(1)概念:在三角形中,连接一个顶点和它所对的边的中点的线段叫做三角形的中线.
(2)三角形的三条中线都在三角形的内部,且交于一点,交点叫三角形的中心,重心把中线分为1:2两部分(到顶点的距离占2份).
3.三角形的高线
(1)概念:从三角形的一个顶点向它的对边所在直线画垂直线,顶点和垂足间的线段叫做三角形的高线.
(2)三角形的三条高或高的延长线交于一点 ( http: / / www.21cnjy.com ),交点叫做三角形的垂心.锐角三角形垂心在三角形的内部,直角三角形的垂心即直角三角形的直角顶点,钝角三角形的垂心在三角形的外部.
4.三角形的中位线
(1)概念:连接三角形两边中点的线段叫做三角形的中位线.
(2)三角形的三条中位线都在三角形的内部,三角形的中位线平行于_____________,且_____________
(二)三角形的性质
1.三角形的三边关系
三角形任意两边之和大于第三边,任意两边之差小于第三边.
判断三条线段是否能组成三角形时,只需要判断较短的两条线段长之和是否大于第三遍即可.
2.三角形的角
(1)三角形的三个内角之和为_____________.
(2)三角形的外角:三角形的一个外角等于_____________ ;三角形的一个外角大于与它不相邻的任何一个内角.
(3)三角形的外角和为________.
(三)全等三角形的判定条件
(1)边角边(SAS):有两边及其夹角对应相等的两个三角形全等.
(2)角边角(ASA):有两角及其夹边对应相等的两个三角形全等.
(3)角角边(AAS):有两角及其一角的对边对应相等的两个三角形全等.
(4)边边边(SSS):三边对应相等的两个三角形全等.
(5)斜边、直角边(HL)(适用于直角三角形):斜边及一直角边对应相等的两个直角三角形全等.
(四)等腰三角形与等边三角形
一、等腰三角形
1.等腰三角形的概念
有两条边相等的三角形,叫做等腰三角形,相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
特别的,三条边都相等的三角形叫做等边三角形.
2等腰三角形的性质
(1)等腰三角形的两个底角相等.
(2)等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.
(3)等腰三角形是轴对称图形.
3.等腰、等边三角形的判定
(1)_____________.
(2)三个内角都相等的三角形是等边三角形.
(3)有_____________的等腰三角形是等边三角形.
(五)角平分线与线段的垂直平分线
1. 角平分线
(1)角平分线的性质:角平分线上的点_____________.
(2)角平分线的判定:到角两边距离相等的点在该角的平分线上.
2. 线段的垂直平分线
(1)概念:经过线段中点,并且垂直于这条线段的直线叫做这条线段的垂直平分线,也叫中垂线.
(2)线段垂直平分线上的点到_____________ 相等.到一条线段的两个端点距离相等的点在这条线段的垂直平分线上.
(六)平行四边形
1.平行四边形的概念与性质:两组对边分别平行的四边形叫做平行四边形.
平行四边形的性质:
平行四边形具有四边形的所有性质.
平行四边形的两组对边分别_____________.
平行四边形的两组对角分别相等,邻角互补.
平行四边形的对角线_____________.
平行四边形是中心对称图形,对称中心是对角线的交点.
2.平行四边形的判定
(1). _____________的四边形是平行四边形.
(2). _____________的四边形是平行四边形.
(3). _____________的四边形是平行四边形.
(4). _____________的四边形是平行四边形.
(5). _____________的四边形是平行四边形.
(七)矩形、菱形
1.矩形
(1).矩形的定义有一个角是直角的平行四边形叫做矩形.
(2).矩形的性质:
①矩形具有平行四边形的一切性质.
②矩形的四个角都是直角.
③矩形的对角线_____________.
(3).矩形的判定定理
①有三个角是直角的四边形是矩形.
②_____________ 是矩形.
③_____________是矩形.
④对角线相等且互相平分的四边形是矩形.
2.菱形
(1)菱形的定义:有一组邻边相等的平行四边形是菱形.
(2)菱形的性质:
①四条边都相等;
②菱形的对角线_____________,并且每一条对角线_____________.
(3)菱形的判定
①________________________是菱形
②__________________________是菱形
③四边相等的四边形是菱形
(八)圆的有关性质及计算
1.垂径定理及其推论
垂径定理:垂直于弦的直径_____________,并且平分_____________.
推论1:①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
②弦的垂直平分线经过圆心角,并且平分弦所对的两条弧;
③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
推论2:圆的两条平行弦所夹的弧______.
2、圆心角、弧、弦和弦心距之间的关系
(1).在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
(2).在同圆或等圆中,如果两个圆心角、两条弦、两条弧或两条两条弦的弦心距中有一组量相等,那么其余的各组量也都分别相等.
3.圆周角定理及其推论
(1)在同圆或等圆中,同弧或等弧所对的圆周 ( http: / / www.21cnjy.com )角_____,都等于它所对的圆心角_____________,这些可以作为证明角相等和角度计算的依据.
(2)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.应用时,常常需要添加辅助线,构成直径所对的圆周角.
4.弧长、扇形的面积
(1).如果弧长为l,圆心角为n°,圆的半径为r,那么弧长的计算公式为_____________
(2).由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
若扇形的圆心角为n°,所在圆的半径为r,弧长为l,面积为S,则_____________
5、圆柱和圆锥
(1).圆柱的侧面积圆柱的侧面展开图为一矩形,矩形的宽为圆柱的高,矩形的长为圆柱的底面圆的周长.
圆柱的侧面积:若圆柱的高为l,底面半径为r,则 =2πrl.
(2).圆锥的侧面积、全面积的计算
圆锥的侧面展开图是以圆锥母线为半径,圆锥底面圆的周长为弧长的扇形.
圆锥的侧面积:圆锥的侧面积是指圆锥侧面展开图的面积,=πrl.
二讲题型——题型解析
(一)全等三角形的性质与判定
例1、如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,E、F分别为BC、AB上的点,AE⊥CF于点G,交CD于点H.
( http: / / www.21cnjy.com )
(1)求证:AH=CF;
(2)若CE=BF,求证:BE=2DH.
(二)等腰三角形的有关计算
例2 如图,在△ABC中,AB=AC,DE是边AB垂直平分线交AB于E,交AC于D,连结BD。
( http: / / www.21cnjy.com )
(1)若∠A=40°,求∠DBC的度数。
(2)若△BCD的周长为12cm,△ABC的周长为18cm,求BE的长。
(三)矩形的判定与性质
例3、如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)求证:BE=DE.
(2)若四边形ABCD的面积为9,求BE的长
(四) 圆的切线的有关计算与证明
例4如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
( http: / / www.21cnjy.com )
(1)求证:AD⊥DC;
(2)若AD=2,AC=,求AB的长.
(五)平行四边形的有关计算与证明
例5 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
( http: / / www.21cnjy.com )
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD= MN.
(六)菱形的性质与证明
例6已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
( http: / / www.21cnjy.com )
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
(七)圆的有关性质与计算
例7如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
( http: / / www.21cnjy.com )
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
三讲方法——方法点睛
(一)证明角或线段的关系:在几何证明与计算 ( http: / / www.21cnjy.com )过程中,若看到边、角的证明,优先考虑证明三角形全等,若告诉两组对应边相等,则优先考虑利用“SAS”找出夹角证明三角形全等;若告诉两组对应角相等,则可以考虑“ASA”、“AAS”;同时,在证明直角三角形全等时,在找角相等,通常利用“同角的余角相等”.
(二)对于一般三角形中的计 ( http: / / www.21cnjy.com )算问题,常用到其性质:三边关系:三角形的两边之和大于第三边,两边之差小于第三边;内角和定理:三角形的内角和等于180°;外角的性质:三角形的一个外角等于与它不相邻的两个内角的和;边角关系:在同一个三角形中,大边对大角,小边对小角.
(三)在平行四边形中若求线段的比,首先 ( http: / / www.21cnjy.com )利用平行四边形的性质,找相似三角形的比例式,找出与要求线段的比有关的比例关系,再利用线段的等量代换求解即可.
(四)在菱形中,若存在一个角为60°,则连接另外两点的对角线所分割的两个三角形为等边三角形,故在计算时,利用等边三角形的性质进行计算.
(五)在菱形的证明过程中,若已知四边形是平行四边形,则只需要证一组邻边相等或对角线互相垂直即可;若相等的边较多,则只需证四条边相等即可.
(六)在利用垂径定理求线段时,通常 ( http: / / www.21cnjy.com )连接半径,作弦心距,利用勾股定理来解答,同时注意半径、弦长的一半、弦心距构成直角三角形,利用勾股定理可以对圆的半径、弦长、弦心距“知二求一”.
(七)在圆的切线证明时,若已知直线 ( http: / / www.21cnjy.com )与圆有公共点,则连接过这点的半径,证明这条半径与直线垂直即可,简记为:有切点,连半径,证垂直;若未知直线与圆有公共点,则过圆心作直线的垂线段,证明垂线段的长等于半径,可简记为:无切点,作垂直,证半径.
(八)阴影部分面积的求法:
①公式法:针对规则的扇形,直接利用公式进行计算即可;
②割补法:针对不规则的图形,可将不规则的图形经过平移或分割转化为几个规则的图形,进行面积的和或差的计算;
③等积变换法:针对不规则的图形,将不规则的图形拼凑成等积的规则图形求解.
四练实题——随堂小练
1. 如图,在矩形ABCD中,AB=3,BC=4,将其折叠,使AB边落在对角线AC上,得到折痕AE,则点E到点B的距离为
( http: / / www.21cnjy.com )
A. B.2 C. D. 3
2. 如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )
( http: / / www.21cnjy.com )
A. B. C. D.
3. 如图,在中,,过顶点的直线,、的平分线分别交于点、,若,,则的长为 .
( http: / / www.21cnjy.com )
4. 如图边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为,,则的值为 .
( http: / / www.21cnjy.com )
5. 如图,矩形ABCD的对角线AC、BD相 ( http: / / www.21cnjy.com )交于点O,DE∥AC,CE∥BD,若AC=4,则四边形CODE的周长为
( http: / / www.21cnjy.com )
6. 如图,点P是菱形ABCD的对角线BD上一点,连结AP、CP,延长CP交AD于E,交BA的延长线于F.
( http: / / www.21cnjy.com )
(1)求证:∠DCP=∠DAP;
(2)若AB=2,DP:PB=1:2,且PA⊥BF,求对角线BD的长.
五练原创——预测提升
1.如图,AB是⊙O的直径,C.D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠BOC=( )
( http: / / www.21cnjy.com )
A.25° B.50° C.130° D.155°
2. 如图,在△ABC中, ( http: / / www.21cnjy.com )边AB的垂直平分线分别交BC于点D,交AB于点E.若AE=3,△ADC的周长为8,则△ABC的周长为 .
( http: / / www.21cnjy.com )
3. 将正方形ABCD中的△ABP绕点B顺时针旋转能与△CBP′重合,若BP=4,则PP′= _________ .
( http: / / www.21cnjy.com )
5. 如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作 ABDE,连接AD,EC.
( http: / / www.21cnjy.com )
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
6. 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
( http: / / www.21cnjy.com )
(1)求证:DE与⊙O相切;
(2)连结AD,己知BC=10,BE=2,求sin∠BAD的值.
同课章节目录
