人教版数学七年级下册 5.1.1 相交线 课件(共24张PPT)
文档属性
| 名称 | 人教版数学七年级下册 5.1.1 相交线 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 09:38:16 | ||
图片预览


文档简介
(共24张PPT)
人教版
七年级下册
5.1.1 相交线
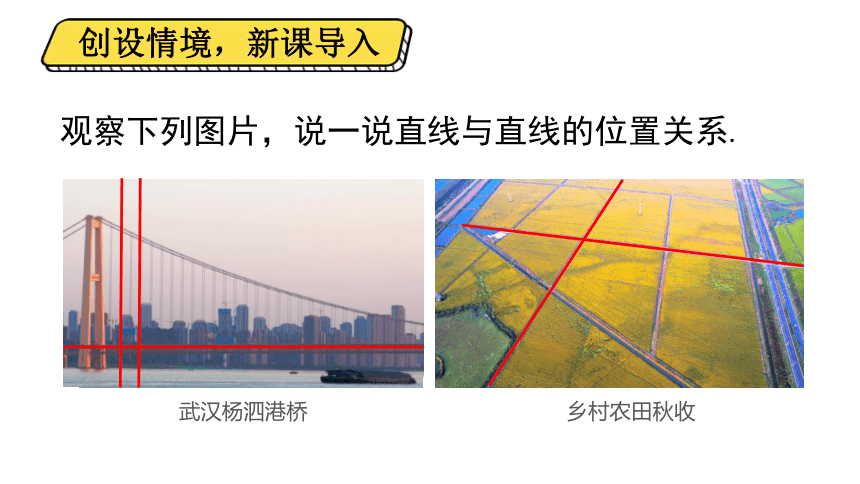
观察下列图片,说一说直线与直线的位置关系.
武汉杨泗港桥
乡村农田秋收
创设情境,新课导入
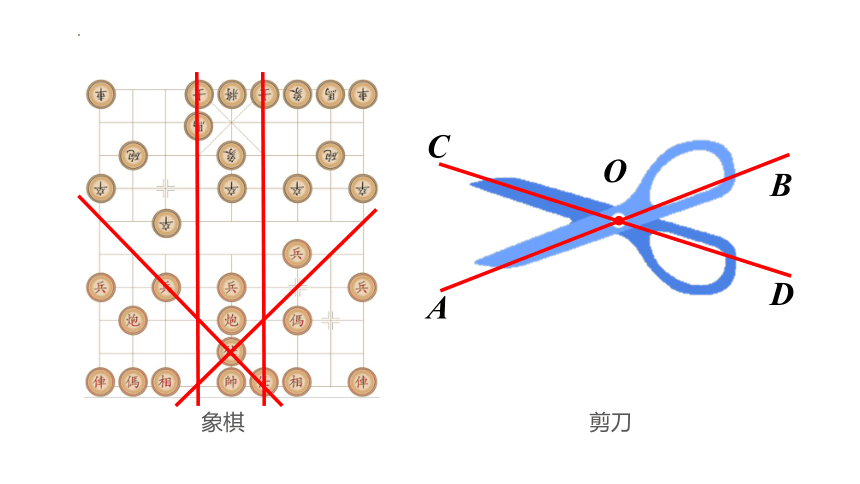
象棋
剪刀
C
D
B
A
O
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点.
这个图形的几何描述为:直线AB,CD相交于点O.
C
D
B
A
O
探究点1:邻补角与对顶角的认识
问题引入,自主探究
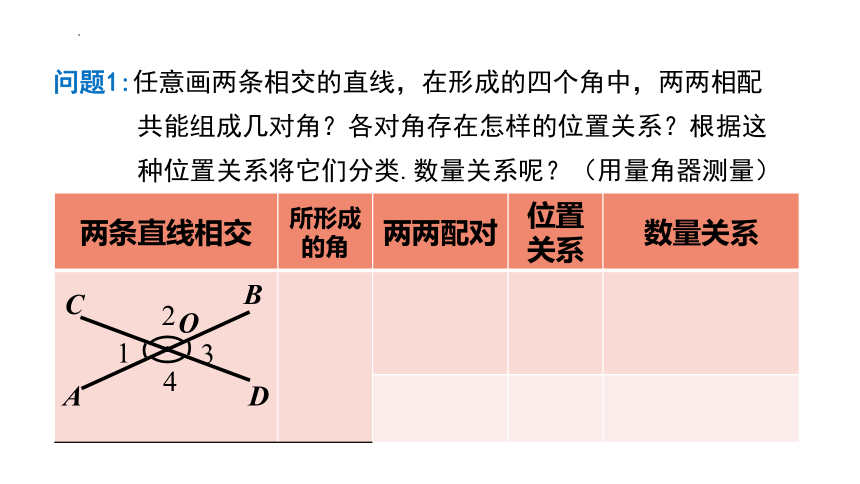
问题1:任意画两条相交的直线,在形成的四个角中,两两相配共能组成几对角?各对角存在怎样的位置关系?根据这种位置关系将它们分类.数量关系呢?(用量角器测量)
两条直线相交 所形成的角 两两配对 位置关系 数量关系
C
D
B
A
O
2
4
1
3
两条直线相交 所形成的角 两两配对 位置关系 数量关系
C
D
B
A
O
2
4
1
3
∠1
∠2
∠3
∠4
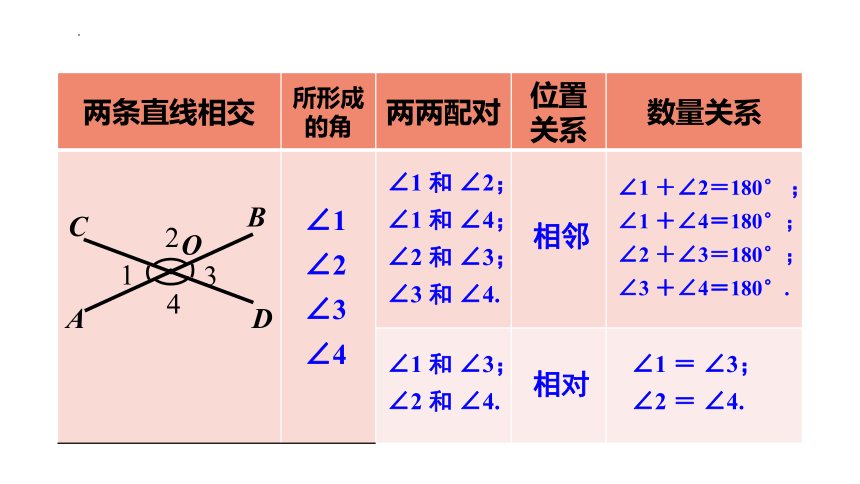
∠1 和 ∠2;
∠1 和 ∠4;
∠2 和 ∠3;
∠3 和 ∠4.
∠1 和 ∠3;
∠2 和 ∠4.
相邻
相对
∠1 +∠2=180° ;
∠1 +∠4=180°;
∠2 +∠3=180°;
∠3 +∠4=180°.
∠1 = ∠3;
∠2 = ∠4.
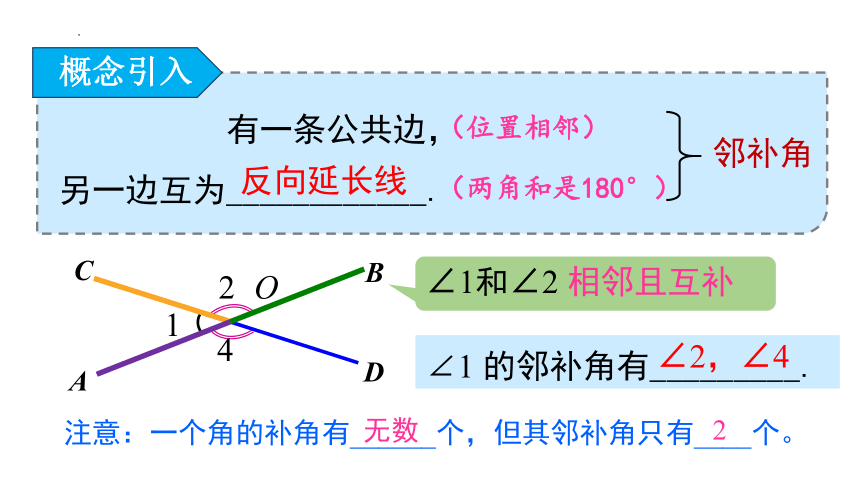
∠1 的邻补角有_________.
1
2
4
A
B
C
D
O
有一条公共边,
另一边互为____________.
反向延长线
∠2,∠4
邻补角
∠1和∠2 相邻且互补
概念引入
(位置相邻)
(两角和是180°)
注意:一个角的补角有______个,但其邻补角只有____个。
无数
2
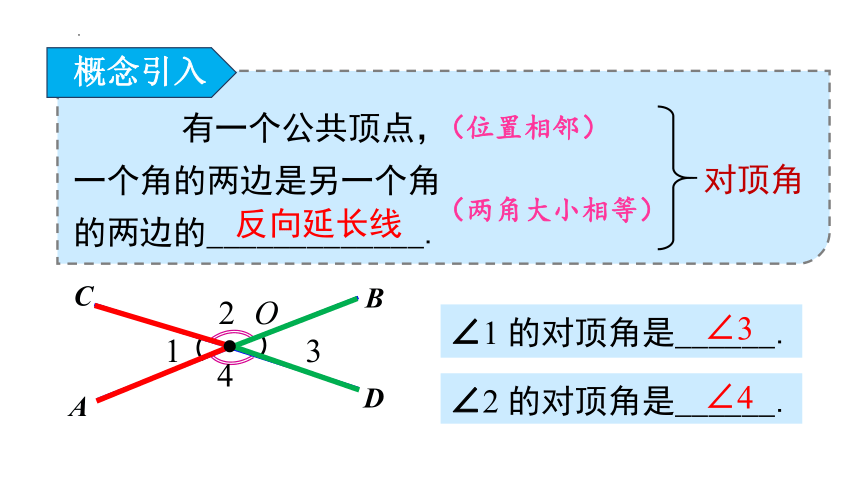
∠1 的对顶角是______.
有一个公共顶点,
一个角的两边是另一个角
的两边的_____________.
反向延长线
∠3
对顶角
概念引入
1
2
4
A
B
C
D
O
∠2 的对顶角是______.
∠4
3
(位置相邻)
(两角大小相等)
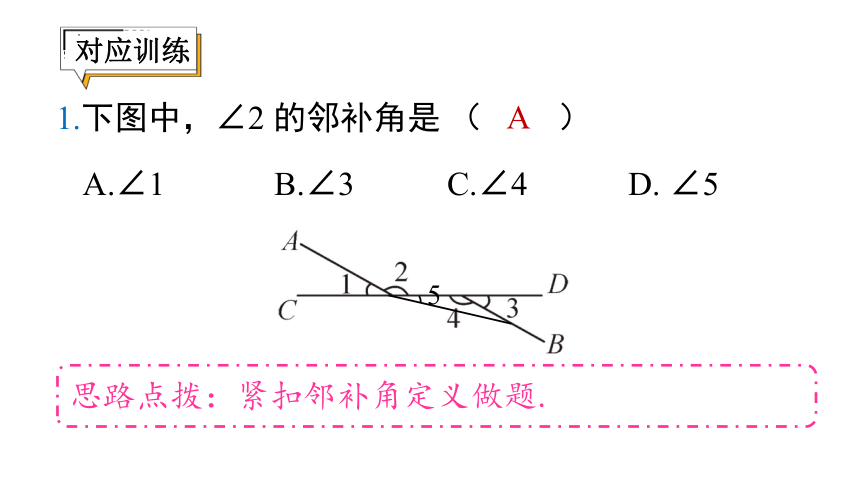
1.下图中,∠2 的邻补角是 ( )
A
思路点拨:紧扣邻补角定义做题.
A.∠1 B.∠3 C.∠4 D. ∠5
5
对应训练
2. 下列图形中, ∠1与∠2互为对顶角的是 ( )
思路点拨:遇到角的辨析,需抓住定义做题.
C
3. 图中的哪些角是邻补角?哪些角是对顶角?
A
C
B
D
E
1
3
2
4
5
6
邻补角:
∠1和∠2;
∠2和∠3;
∠3和∠4;
∠4和∠1;
∠5和∠6.
对顶角:
∠1和∠3;
∠2和∠4;
注意:如果一条直线与射线相交(端点在直线上),也
可以得到一对领补角。
问题2:观察剪刀工作过程,剪刀的张角发生了改变,邻补角与对顶角的数量关系是否仍存在?如何证明?
C
D
B
A
O
2
4
1
3
探究点2:邻补角与对顶角的性质
∠1 = ∠3
∠1 + ∠2 =180°
归纳总结
方法一:量角器测量各个角的度数:
∠1 ∠2 ∠3 ∠4
方法二:几何推导证明:
∵ ∠1 与∠2 互补,∠3 与∠2 互补(邻补角的定义),
∴ ∠1=∠3 (同角的补角相等).
邻补角互补(两角之和为180°),对顶角相等.
C
D
B
A
O
2
4
1
3
例1 如图所示,直线 a,b 相交,∠1 = 40°,
求∠2,∠3,∠4 的度数.
已知角
未知角
邻补角的定义
对顶角的性质
分析:
【教材P3 例1】
解:由邻补角的定义,得
∠2 = 180°-∠1
=180°- 40°= 140°;
由对顶角相等,得
∠3 =∠1 =40°,∠4 =∠2 = 140°.
总结
几何中角度的计算,常常将未知角转化为已知角,通过列方程或简单计算求解.
40°
140°
40°
140°
1.如图,直线AB,CD相交于点O,若∠AOD减小30°, 则∠BOC ( )
A.增大30°
B.增大150°
C.不变
D.减小30°
D
对应训练
2. 如图,要测量两堵围墙形成的∠AOB的度数,先分别延长AO,BO得到∠COD,然后通过测量∠COD的度数从而得到∠AOB的度数,其中运用的原理是______________﹒
对顶角相等
3. 如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗 两根木条所成的角中,如果∠α=35°,其他三个角各等于多少度?如果∠α等于90°,115°,m°呢
a
α
b
【选自教材P3 练习】
如果∠α是35°,其他三个角分别是145°,35°,145°;
∠α是90°,其他三个角都是90°;
∠α是115°,其他三个角分别是65°,115°,65°;
∠α是m°,其他三个角分别是(180-m)°,m°,(180-m)°.
a
α
b
例2 如图,直线AB和CD相交于点O,OE平分∠AOD.若∠1+∠2=80°,求∠AOE的度数.
重点突破,提升探究
解:由对顶角相等,得∠1=∠2,
因为∠1+∠2=80°,
由邻补角的定义,得
∠AOD=180°-∠1=180°-40°=140°.
因为OE平分∠AOD,
所以∠1=∠2= ×80°=40°,
所以∠AOE= ∠AOD= ×140°=70°.
1.如图,直线CD与EF相交于点O,OC平分∠AOF.
若∠AOE=40°,求∠DOE的度数.
解:因为∠AOE=40°,
因为∠AOF=180°-∠AOE=140°.
因为OC平分∠AOF,
所以∠DOE= ∠COF=70°,
所以∠DOE的度数为70°.
所以∠COF= ∠AOF=70°,
对应训练
2.
邻补角定义
有一条公共边,
另一边互为反向延长线,
对顶角定义
有公共顶点,
两边互为反向延长线,
(位置相邻)
(数量互补)
(位置相对)
(数量相等)
的两个角;
的两个角;
n条直线相交于一点就有( )对对顶角,( )对邻补角.
n(n-1)
2n(n-1)
什么是邻补角?邻补角与补角有什么区别和联系?
什么是对顶角?对顶角有什么性质?
相交线
两条直线相交
邻补角
邻补角互补
对顶角
邻补角相等
一般情况
回顾内容,课堂总结
人教版
七年级下册
5.1.1 相交线
观察下列图片,说一说直线与直线的位置关系.
武汉杨泗港桥
乡村农田秋收
创设情境,新课导入
象棋
剪刀
C
D
B
A
O
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点.
这个图形的几何描述为:直线AB,CD相交于点O.
C
D
B
A
O
探究点1:邻补角与对顶角的认识
问题引入,自主探究
问题1:任意画两条相交的直线,在形成的四个角中,两两相配共能组成几对角?各对角存在怎样的位置关系?根据这种位置关系将它们分类.数量关系呢?(用量角器测量)
两条直线相交 所形成的角 两两配对 位置关系 数量关系
C
D
B
A
O
2
4
1
3
两条直线相交 所形成的角 两两配对 位置关系 数量关系
C
D
B
A
O
2
4
1
3
∠1
∠2
∠3
∠4
∠1 和 ∠2;
∠1 和 ∠4;
∠2 和 ∠3;
∠3 和 ∠4.
∠1 和 ∠3;
∠2 和 ∠4.
相邻
相对
∠1 +∠2=180° ;
∠1 +∠4=180°;
∠2 +∠3=180°;
∠3 +∠4=180°.
∠1 = ∠3;
∠2 = ∠4.
∠1 的邻补角有_________.
1
2
4
A
B
C
D
O
有一条公共边,
另一边互为____________.
反向延长线
∠2,∠4
邻补角
∠1和∠2 相邻且互补
概念引入
(位置相邻)
(两角和是180°)
注意:一个角的补角有______个,但其邻补角只有____个。
无数
2
∠1 的对顶角是______.
有一个公共顶点,
一个角的两边是另一个角
的两边的_____________.
反向延长线
∠3
对顶角
概念引入
1
2
4
A
B
C
D
O
∠2 的对顶角是______.
∠4
3
(位置相邻)
(两角大小相等)
1.下图中,∠2 的邻补角是 ( )
A
思路点拨:紧扣邻补角定义做题.
A.∠1 B.∠3 C.∠4 D. ∠5
5
对应训练
2. 下列图形中, ∠1与∠2互为对顶角的是 ( )
思路点拨:遇到角的辨析,需抓住定义做题.
C
3. 图中的哪些角是邻补角?哪些角是对顶角?
A
C
B
D
E
1
3
2
4
5
6
邻补角:
∠1和∠2;
∠2和∠3;
∠3和∠4;
∠4和∠1;
∠5和∠6.
对顶角:
∠1和∠3;
∠2和∠4;
注意:如果一条直线与射线相交(端点在直线上),也
可以得到一对领补角。
问题2:观察剪刀工作过程,剪刀的张角发生了改变,邻补角与对顶角的数量关系是否仍存在?如何证明?
C
D
B
A
O
2
4
1
3
探究点2:邻补角与对顶角的性质
∠1 = ∠3
∠1 + ∠2 =180°
归纳总结
方法一:量角器测量各个角的度数:
∠1 ∠2 ∠3 ∠4
方法二:几何推导证明:
∵ ∠1 与∠2 互补,∠3 与∠2 互补(邻补角的定义),
∴ ∠1=∠3 (同角的补角相等).
邻补角互补(两角之和为180°),对顶角相等.
C
D
B
A
O
2
4
1
3
例1 如图所示,直线 a,b 相交,∠1 = 40°,
求∠2,∠3,∠4 的度数.
已知角
未知角
邻补角的定义
对顶角的性质
分析:
【教材P3 例1】
解:由邻补角的定义,得
∠2 = 180°-∠1
=180°- 40°= 140°;
由对顶角相等,得
∠3 =∠1 =40°,∠4 =∠2 = 140°.
总结
几何中角度的计算,常常将未知角转化为已知角,通过列方程或简单计算求解.
40°
140°
40°
140°
1.如图,直线AB,CD相交于点O,若∠AOD减小30°, 则∠BOC ( )
A.增大30°
B.增大150°
C.不变
D.减小30°
D
对应训练
2. 如图,要测量两堵围墙形成的∠AOB的度数,先分别延长AO,BO得到∠COD,然后通过测量∠COD的度数从而得到∠AOB的度数,其中运用的原理是______________﹒
对顶角相等
3. 如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗 两根木条所成的角中,如果∠α=35°,其他三个角各等于多少度?如果∠α等于90°,115°,m°呢
a
α
b
【选自教材P3 练习】
如果∠α是35°,其他三个角分别是145°,35°,145°;
∠α是90°,其他三个角都是90°;
∠α是115°,其他三个角分别是65°,115°,65°;
∠α是m°,其他三个角分别是(180-m)°,m°,(180-m)°.
a
α
b
例2 如图,直线AB和CD相交于点O,OE平分∠AOD.若∠1+∠2=80°,求∠AOE的度数.
重点突破,提升探究
解:由对顶角相等,得∠1=∠2,
因为∠1+∠2=80°,
由邻补角的定义,得
∠AOD=180°-∠1=180°-40°=140°.
因为OE平分∠AOD,
所以∠1=∠2= ×80°=40°,
所以∠AOE= ∠AOD= ×140°=70°.
1.如图,直线CD与EF相交于点O,OC平分∠AOF.
若∠AOE=40°,求∠DOE的度数.
解:因为∠AOE=40°,
因为∠AOF=180°-∠AOE=140°.
因为OC平分∠AOF,
所以∠DOE= ∠COF=70°,
所以∠DOE的度数为70°.
所以∠COF= ∠AOF=70°,
对应训练
2.
邻补角定义
有一条公共边,
另一边互为反向延长线,
对顶角定义
有公共顶点,
两边互为反向延长线,
(位置相邻)
(数量互补)
(位置相对)
(数量相等)
的两个角;
的两个角;
n条直线相交于一点就有( )对对顶角,( )对邻补角.
n(n-1)
2n(n-1)
什么是邻补角?邻补角与补角有什么区别和联系?
什么是对顶角?对顶角有什么性质?
相交线
两条直线相交
邻补角
邻补角互补
对顶角
邻补角相等
一般情况
回顾内容,课堂总结
