2015年中考数学二轮专题复习教案:专题05 一次函数、反比例函数的图象和性质
文档属性
| 名称 | 2015年中考数学二轮专题复习教案:专题05 一次函数、反比例函数的图象和性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 153.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-05 00:00:00 | ||
图片预览


文档简介
备战2015年中考二轮讲练测
第一篇 专题整合篇
专题05一次函数、反比例函数的图象和性质(讲案)
一讲考点——考点梳理
(一)概念
1、一次函数:一般地,如果(k,b ,k ),那么y叫做x的一次函数.
正比例函数:特别地,当一次函数中的b为0时,(k为常数,k0).这时,y叫做x的正比例函数.
2.反比例函数:一般地,形如 (k为常数,k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.自变量x的取值范围是不等于0的一切实数.
反比例函数也可表示成:y = kx-1 (k为常数,k≠0)或xy = k(k为常数,k≠0)
(二)函数的图象
1.一次函数的图象:所有一次函数的图象都是一条
2.反比例函数的图象:
(三)函数图象的主要特征
1.一次函数的图象是经过点(0,b)的直线;正比例函数的图象是经过原点(0,0)的直线;|k|越大,直线越陡,|k|越小直线越缓.
2.反比例函数y=的图象与坐标轴没有交点;|k|越大,图象的弯曲度越小,曲线越平直.|k|越小,图象的弯曲度越大.
(四)函数的性质
1.正比例函数的性质
一般地,正比例函数有下列性质:
(1)当k>0时,图象经过第一、三象限,y随x的增大而 ;
(2)当k<0时,图象经过第二、四象限,y随x的增大而 .
2.一次函数的性质
一般地,一次函数有下列性质:
(1)当k>0时,y随x的增大而
(2)当k<0时,y随x的增大而
3.反比例函数的性质
一般地,反比例函数y=有下列性质:
(1)当k>0时,图象的两支分别位于一、三象限;在 内,y随x的增大而 ;
(2)当k>0时,图象的两支分别位于二、四象限;在 内,y随x的增大而 .
(五)函数解析式的确定
待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
(六)反比例函数y=(k为常数,k≠0)中k的几何意义
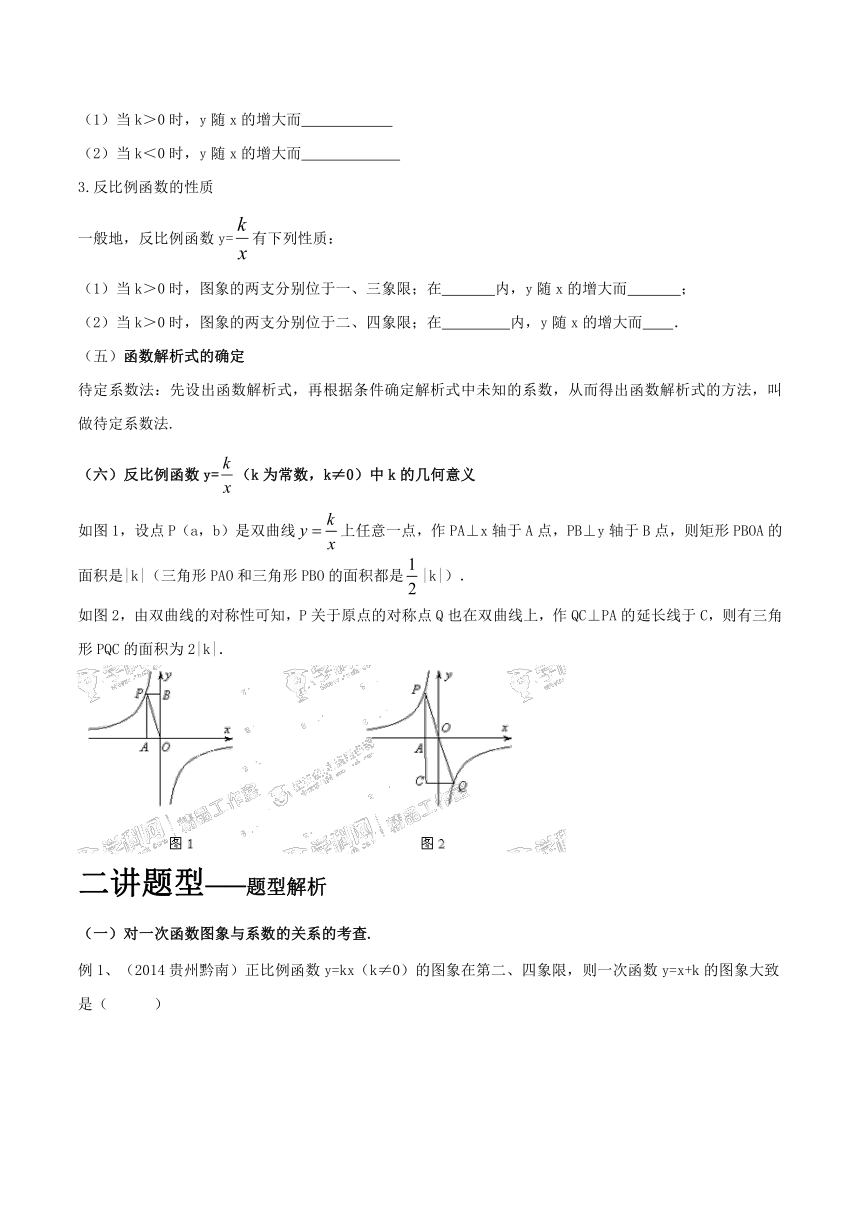
如图1,设点P(a,b)是双曲线上任意一点,作PA⊥x轴于A点,PB⊥y轴于B点,则矩形PBOA的面积是|k|(三角形PAO和三角形PBO的面积都是|k|).
如图2,由双曲线的对称性可知,P关于原点的对称点Q也在双曲线上,作QC⊥PA的延长线于C,则有三角形PQC的面积为2|k|.
( http: / / www.21cnjy.com )
二讲题型——题型解析
(一)对一次函数图象与系数的关系的考查.
例1、(2014贵州黔南)正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
(二)对一次函数图象与几何变换的考查.
例2、(2014江苏徐州)将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A. B. C. D.
(三)对两条直线相交或平行的考查
例3、(2014宜宾)如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
( http: / / www.21cnjy.com )
A. y=2x+3 B. y=x﹣3 C. y=2x﹣3 D. y=﹣x+3
(四)对反比例函数图象和性质的考查
例4、(2014杭州)函数的自变量x满足时,函数值y满足,则这个函数可以是( )
A. B. C. D.
(五) 对函数增减性的考查
例5、(2014贵州安顺)如果点A(﹣2,y1),B(﹣1,y2),C(2,y3)都在反比例函数的图象上,那么y1,y2,y3的大小关系是( )
A. y1<y3<y2 B. y2<y1<y3 C. y1<y2<y3 D. y3<y2<y1
对待定系数法的考查
例6、(2014桂林)一次函数y=kx+b(k≠0)的图像如图所示,则下列结论正确的是( )
( http: / / www.21cnjy.com )
A.k=2 B.k=3 C.b=2 D.b=3
对面积计算的考查
例7、(2014抚顺)如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
( http: / / www.21cnjy.com )
A. 逐渐增大 B. 不变 C. 逐渐减小 D. 先增大后减小
对一次函数与反比例函数综合的考查
例8.(2014眉山)如图,直线与x轴交于点B,双曲线交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为( )
A.2 B.3 C.4 D.6
( http: / / www.21cnjy.com )
三讲方法——方法点睛
(一)解决有关函数的问题主要要结合图象进行
(1)正比例函数图象上点的纵坐标y与横坐标 ( http: / / www.21cnjy.com )x之比,是固定不变的,等于常量k.图象在横轴上方的部分都有y>0;在横轴下方的部分都有y<0;与横轴的交点都有y=0.
(2)直线y=kx+b(k≠0)与直线y= ( http: / / www.21cnjy.com )kx平行,是由直线y=kx平移不|b|个单位得到的,平移的方向,当b>0时,向上;当b<0时,向下.
(3)对于一次函数的一次项 ( http: / / www.21cnjy.com )系数k,当k>0时,y随x的增大而增大,从左向右看,直线呈上升趋势,当k<0时,y随x的增大而减小,从左向右看,直线呈下降趋势.
(二)运用待定系数法时,常用的方法是: ( http: / / www.21cnjy.com )按所求的函数类型,设也解析式;把题目中提供的坐标代入所设解析式中;解这个方程或者方程组;解这个方程或方程组,得到待定系数的值;将求出的结果代入所设的解析式中,得到函数解析式.
通常,有几个待定系数,就要列几个方程,也就需要几个点的坐标.
(三)解决两个函数图象在同一坐标系中表示的时候,要注意相同字母的取值是一样的,解选择题时,通常用排除法.
四练实题——随堂小练
1.函数y=x-1的图象是( )
( http: / / www.21cnjy.com )
2.已知反比例函数y=的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
A. (﹣6,1) B. (1,6) C. (2,﹣3) D. (3,﹣2)
3.将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A. B. C. D.
4.如图,直线与x轴交于点B,双曲线交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为( )
A.2 B.3 C.4 D.6
( http: / / www.21cnjy.com )
5.已知k1>0>k2,则函数y=k1x和y=的图象在同一平面直角坐标系中大致是( )A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.如图,一次函数y=kx﹣1的图象与x轴交于点A,与反比例函数(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 .
( http: / / www.21cnjy.com )
五练原创——预测提升
1.已知函数y=ax+b经过(2,4),(1,﹣1),则a﹣b=( )
A.1 B.﹣5 C.5 D.11
2.如图,函数y=x和y=ax+3的图象相交于点A(m,4),则不等式x≥ax+3的解集为( )
( http: / / www.21cnjy.com )
A.x≥4 B.x≤4 C.x≤2 D.x≥2
3.反比例函数在每个象限内的函数值随的增大而减小,则的取值范围是( )
A. B. C. D.
4.已知如图,一次函数y=ax+b和反比例函数的图象相交于A、B两点,不等式ax+b>的解集为( )
( http: / / www.21cnjy.com )
A. x<﹣3 B. ﹣3<x<0或x>1 C. x<﹣3或x>1 D. ﹣3<x<1
5.如图,A、B两点在双曲线y=上,分别经过A、B两点向轴作垂线段,已知S阴影=2,则S1+S2=( )
( http: / / www.21cnjy.com )
A. 3 B. 4 C. 5 D. 6
6.在平面直角坐标系xOy中,直线与y轴交于点A.
(1)如图,直线与直线交于点B,与y轴交于点C,点B横坐标为.
①求点B的坐标及k的值;
②直线与直线与y轴所围成的△ABC的面积等于 ;
(2)直线与x轴交于点E(,0),若,求k的取值范围.
( http: / / www.21cnjy.com )
第一篇 专题整合篇
专题05一次函数、反比例函数的图象和性质(讲案)
一讲考点——考点梳理
(一)概念
1、一次函数:一般地,如果(k,b ,k ),那么y叫做x的一次函数.
正比例函数:特别地,当一次函数中的b为0时,(k为常数,k0).这时,y叫做x的正比例函数.
2.反比例函数:一般地,形如 (k为常数,k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.自变量x的取值范围是不等于0的一切实数.
反比例函数也可表示成:y = kx-1 (k为常数,k≠0)或xy = k(k为常数,k≠0)
(二)函数的图象
1.一次函数的图象:所有一次函数的图象都是一条
2.反比例函数的图象:
(三)函数图象的主要特征
1.一次函数的图象是经过点(0,b)的直线;正比例函数的图象是经过原点(0,0)的直线;|k|越大,直线越陡,|k|越小直线越缓.
2.反比例函数y=的图象与坐标轴没有交点;|k|越大,图象的弯曲度越小,曲线越平直.|k|越小,图象的弯曲度越大.
(四)函数的性质
1.正比例函数的性质
一般地,正比例函数有下列性质:
(1)当k>0时,图象经过第一、三象限,y随x的增大而 ;
(2)当k<0时,图象经过第二、四象限,y随x的增大而 .
2.一次函数的性质
一般地,一次函数有下列性质:
(1)当k>0时,y随x的增大而
(2)当k<0时,y随x的增大而
3.反比例函数的性质
一般地,反比例函数y=有下列性质:
(1)当k>0时,图象的两支分别位于一、三象限;在 内,y随x的增大而 ;
(2)当k>0时,图象的两支分别位于二、四象限;在 内,y随x的增大而 .
(五)函数解析式的确定
待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
(六)反比例函数y=(k为常数,k≠0)中k的几何意义
如图1,设点P(a,b)是双曲线上任意一点,作PA⊥x轴于A点,PB⊥y轴于B点,则矩形PBOA的面积是|k|(三角形PAO和三角形PBO的面积都是|k|).
如图2,由双曲线的对称性可知,P关于原点的对称点Q也在双曲线上,作QC⊥PA的延长线于C,则有三角形PQC的面积为2|k|.
( http: / / www.21cnjy.com )
二讲题型——题型解析
(一)对一次函数图象与系数的关系的考查.
例1、(2014贵州黔南)正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
(二)对一次函数图象与几何变换的考查.
例2、(2014江苏徐州)将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A. B. C. D.
(三)对两条直线相交或平行的考查
例3、(2014宜宾)如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
( http: / / www.21cnjy.com )
A. y=2x+3 B. y=x﹣3 C. y=2x﹣3 D. y=﹣x+3
(四)对反比例函数图象和性质的考查
例4、(2014杭州)函数的自变量x满足时,函数值y满足,则这个函数可以是( )
A. B. C. D.
(五) 对函数增减性的考查
例5、(2014贵州安顺)如果点A(﹣2,y1),B(﹣1,y2),C(2,y3)都在反比例函数的图象上,那么y1,y2,y3的大小关系是( )
A. y1<y3<y2 B. y2<y1<y3 C. y1<y2<y3 D. y3<y2<y1
对待定系数法的考查
例6、(2014桂林)一次函数y=kx+b(k≠0)的图像如图所示,则下列结论正确的是( )
( http: / / www.21cnjy.com )
A.k=2 B.k=3 C.b=2 D.b=3
对面积计算的考查
例7、(2014抚顺)如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
( http: / / www.21cnjy.com )
A. 逐渐增大 B. 不变 C. 逐渐减小 D. 先增大后减小
对一次函数与反比例函数综合的考查
例8.(2014眉山)如图,直线与x轴交于点B,双曲线交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为( )
A.2 B.3 C.4 D.6
( http: / / www.21cnjy.com )
三讲方法——方法点睛
(一)解决有关函数的问题主要要结合图象进行
(1)正比例函数图象上点的纵坐标y与横坐标 ( http: / / www.21cnjy.com )x之比,是固定不变的,等于常量k.图象在横轴上方的部分都有y>0;在横轴下方的部分都有y<0;与横轴的交点都有y=0.
(2)直线y=kx+b(k≠0)与直线y= ( http: / / www.21cnjy.com )kx平行,是由直线y=kx平移不|b|个单位得到的,平移的方向,当b>0时,向上;当b<0时,向下.
(3)对于一次函数的一次项 ( http: / / www.21cnjy.com )系数k,当k>0时,y随x的增大而增大,从左向右看,直线呈上升趋势,当k<0时,y随x的增大而减小,从左向右看,直线呈下降趋势.
(二)运用待定系数法时,常用的方法是: ( http: / / www.21cnjy.com )按所求的函数类型,设也解析式;把题目中提供的坐标代入所设解析式中;解这个方程或者方程组;解这个方程或方程组,得到待定系数的值;将求出的结果代入所设的解析式中,得到函数解析式.
通常,有几个待定系数,就要列几个方程,也就需要几个点的坐标.
(三)解决两个函数图象在同一坐标系中表示的时候,要注意相同字母的取值是一样的,解选择题时,通常用排除法.
四练实题——随堂小练
1.函数y=x-1的图象是( )
( http: / / www.21cnjy.com )
2.已知反比例函数y=的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
A. (﹣6,1) B. (1,6) C. (2,﹣3) D. (3,﹣2)
3.将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A. B. C. D.
4.如图,直线与x轴交于点B,双曲线交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为( )
A.2 B.3 C.4 D.6
( http: / / www.21cnjy.com )
5.已知k1>0>k2,则函数y=k1x和y=的图象在同一平面直角坐标系中大致是( )A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.如图,一次函数y=kx﹣1的图象与x轴交于点A,与反比例函数(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是 .
( http: / / www.21cnjy.com )
五练原创——预测提升
1.已知函数y=ax+b经过(2,4),(1,﹣1),则a﹣b=( )
A.1 B.﹣5 C.5 D.11
2.如图,函数y=x和y=ax+3的图象相交于点A(m,4),则不等式x≥ax+3的解集为( )
( http: / / www.21cnjy.com )
A.x≥4 B.x≤4 C.x≤2 D.x≥2
3.反比例函数在每个象限内的函数值随的增大而减小,则的取值范围是( )
A. B. C. D.
4.已知如图,一次函数y=ax+b和反比例函数的图象相交于A、B两点,不等式ax+b>的解集为( )
( http: / / www.21cnjy.com )
A. x<﹣3 B. ﹣3<x<0或x>1 C. x<﹣3或x>1 D. ﹣3<x<1
5.如图,A、B两点在双曲线y=上,分别经过A、B两点向轴作垂线段,已知S阴影=2,则S1+S2=( )
( http: / / www.21cnjy.com )
A. 3 B. 4 C. 5 D. 6
6.在平面直角坐标系xOy中,直线与y轴交于点A.
(1)如图,直线与直线交于点B,与y轴交于点C,点B横坐标为.
①求点B的坐标及k的值;
②直线与直线与y轴所围成的△ABC的面积等于 ;
(2)直线与x轴交于点E(,0),若,求k的取值范围.
( http: / / www.21cnjy.com )
同课章节目录
