2015年中考数学二轮专题复习教案:专题12 统计与概率
文档属性
| 名称 | 2015年中考数学二轮专题复习教案:专题12 统计与概率 |  | |
| 格式 | zip | ||
| 文件大小 | 83.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-05 08:52:14 | ||
图片预览



文档简介
备战2015年中考二轮讲练测
第一篇 专题整合篇
专题12 统计与概率(讲案)
一讲考点——考点梳理
总体与样本
1.我们考察的对象一般是具体问题里的某种数量指标,也就是说,总体实质上是一些”数“的总体,而不是”物“的全体
2.样本中个体的数目叫样本容量,样本是由有限的一部分个体组成,样本的容量是正整数(没有单位)
(二)频数分布直方图
1.条形图和直方图的区别
(1)条形图是用条形的高度表示频数的大小,而直方图实际上是用长方形的面积表示频
(2)条形图中,横轴上的数据是孤立的,是一个具体的数据,而直方图中,横轴上的数据是连续的,是一个范围.
(3)条形图中,各长方形之间有空隙,而直方图中,各长方形是靠在一起的.
2.与频数.频数相关的公式
(1)频数=频率×总数.
(2)各组频数之和等于总数.
(3)各组频率之和等于1
(三)事件类型
事件类型 定义 举例 概率
确定事件 必然事件 一定会发生的事件 “投一枚骰子,出现的点数大于0”是必然事件 1
不可能事件 一定不会发生的事件 “投一枚骰子,出现的点数是7”是不可能事件 0
随机事件 可能发生也可能不发生的事件 “抛投一枚硬币,出现正面朝上”是随机事件 0~1之间
(四)方差
1.方差和极差都能表示一组数据的离散程度.极差表示一组数据的变化范围,方差表示一组数据的波动大小.
2.极差大只能说明这组数据中最大值与最小值的离散程度大小,但不能表示其他数据的波动大小,即极差不能准确地衡量数据的波动程度.
3.在样本容量相同的情况下,方差越大,说明数据波动越大,越不稳定;方差越小,说明数据波动越小,越稳定.
(五)概率
1.概率公式:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=.
2.用频率估计概率
一般地,在大量重复试验中,如果事件A发生的频率n分之m会稳定在某个常数p附近,那么事件A发生的概率P(A)=p.
二讲题型——题型解析
(一)统计图的综合应用
例1 近期国家颁布禁令,禁止在公共场合吸烟。禁令颁布后,小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:
A.顾客出面制止;
B.劝说到室外吸烟;
C.餐厅工作人员出面制止;
D.无所谓.
他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
( http: / / www.21cnjy.com )
(1)这次抽样调查的人数有 人;
(2)请将统计图①补充完整;
(3)在统计图②中,“无所谓”部分所对应的圆心角是 度;
(4)若城区人口有400万人,估计赞成“餐厅工作人员出面制止”的有多少万人?
(二)众数、中位数、平均数
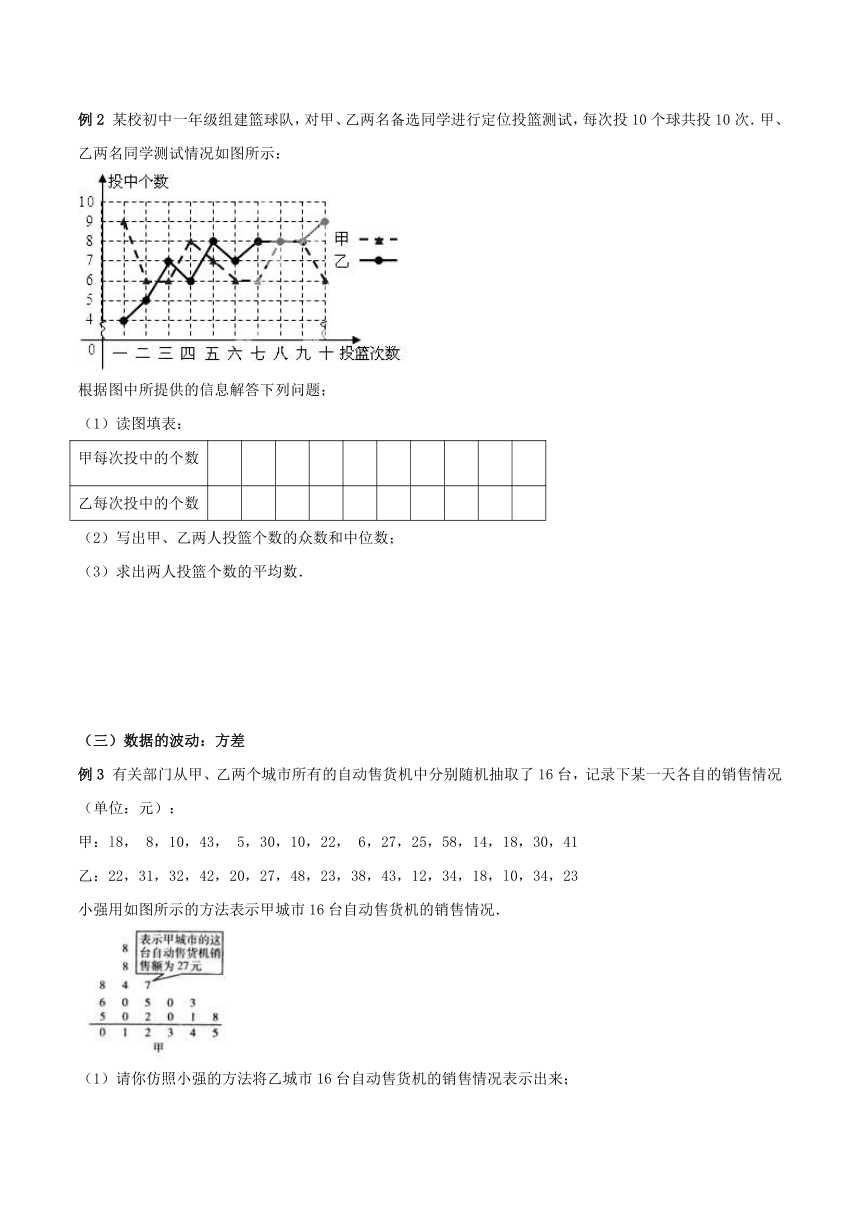
例2 某校初中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球共投10次.甲、乙两名同学测试情况如图所示:
( http: / / www.21cnjy.com )
根据图中所提供的信息解答下列问题;
(1)读图填表:
甲每次投中的个数
乙每次投中的个数
(2)写出甲、乙两人投篮个数的众数和中位数;
(3)求出两人投篮个数的平均数.
(三)数据的波动:方差
例3 有关部门从甲、乙两个城市所有的自动售货机中分别随机抽取了16台,记录下某一天各自的销售情况(单位:元):
甲:l8, 8,10,43, 5,30,10,22, 6,27,25,58,14,18,30,41
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,l0,34,23
小强用如图所示的方法表示甲城市16台自动售货机的销售情况.
( http: / / www.21cnjy.com )
(1)请你仿照小强的方法将乙城市16台自动售货机的销售情况表示出来;
(2)用不等号填空:甲_____乙;s_____s;
(3)请说出此种表示方法的优点.
(四)概率公式
例4 一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程有两个不相等实数根的概率.
(五)概率中的放回与不放回问题
例5 在一个不透明的布口袋中装有只有颜色不同,其他都相同的白、红、黑三种颜色的小球各只,甲、乙两人进行摸球游戏:甲先从袋中摸出一球,看清颜色后放回,再由乙从袋中摸出一球.
(1)试用树状图(或列表法)表示摸球游戏所有可能的结果;
(2)如果规定:乙摸到与甲相同颜色的球为乙胜,否则为甲胜,问谁在游戏中获胜的可能性更大些?
(六)游戏中的概率问题
例6 一个不透明的口袋中装有4个完全相同 ( http: / / www.21cnjy.com )的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
( http: / / www.21cnjy.com )
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
三讲方法——方法点睛
1.样本的几点说明:(1)样本的提取是否得 ( http: / / www.21cnjy.com )当直接关系到对总体估计的准确度,因此为了获得较准确的调查结果,抽取的样本要具有代表性和广泛性.(2)总体和样本的关系:总体包括所有个体,样本只包含一部分个体.样本是总体的一部分,总体可以有多个样本,一个样本在一定程度上反映总体.(3)样本容量是样本中个体的数目.一般的,样本容量越大,通过样本对总体的估计越准确.在实际情况中,要根据具体情况确定样本容量的大小.
2.统计图的分析有:条形统计图、扇形统计图 ( http: / / www.21cnjy.com )、折线统计图三种,条形统计图能清晰地显示每组数据的具体值,折线统计图能确切地表示出各部分的具体值,还能显示出各个数据的变化趋势;扇形统计图能够清楚地表示各部分在总体中所占的百分比.
3.众数、中位数
众数是指一组数据中出现次数 ( http: / / www.21cnjy.com )最多的数,它可以有多个;中位数是指将一组数据按从大到小(或从小到大)的顺序排列后,位于最中间的一个数或两个数的平均数,计算时要分清是奇数个还是偶数个.
4.平均数
一组数据的平均数是,若所占的权分别是,则加权平均数是.
5. 常见的求概率的方法
(1).列举法
在一次实验中,如果可能出现的结果只有有 ( http: / / www.21cnjy.com )限个,且各种结果出现的可能性大小相等,我们可以通过列举试验结果的方法,分析出随机事件发生的概率,这种方法称为列举法.
(2).画树状图法
通过画树状图列出列出某事件的所有可 ( http: / / www.21cnjy.com )能的结果,求出其概率的方法叫做树状图法.当一次试验要涉及三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果, 通常采用树状图法求概率.
(3).列表法
用列出表格的方法来分析和求解某些事 ( http: / / www.21cnjy.com )件的概率的方法叫做列表法.当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.
四练实题——随堂小练
1、下列说法正确的是( )
A. 了解某班同学的身高情况适合用全面调查
B. 数据2、3、4、2、3的众数是2
C. 数据4、5、5、6、0的平均数是5
D. 甲、乙两组数据的平均数相同,方差分别是,则甲组数据更稳定
2、在市教育局举行的“经典诗朗诵”演讲比赛中 ( http: / / www.21cnjy.com ),有11名学生参加决赛,他们决赛的成绩各不相同,其中的一名学生想知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
3、一个袋中只装有3个红球,从中随机摸出一个是红球( )
A. 可能性为 B. 属于不可能事件 C. 属于随机事件 D. 属于必然事件
4、甲、乙、丙三位同学打乒 ( http: / / www.21cnjy.com )乓球,想通过“手心手背”游戏来决定其中哪两个人先打,规则如下:三个人同时各用一只手随机出示手心或手背,若只有两个人手势相同(都是手心或都是手背),则这两人先打,若三人手势相同,则重新决定.那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是 .
5、把形状、大小、质地完全相同的4张卡片分别标上数字﹣1、﹣4、0、2,将这4张卡片放入不透明的盒子中搅匀.求下列事件的概率:
(1)从中随机抽取一张卡片,卡片上的数字是负数;
(2)先从盒子中随机抽取一张卡片不放回,再随机抽取一张,两张卡片上的数字之积为0(用列表法或树形图).
6、某中学组织网络安全知 ( http: / / www.21cnjy.com )识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
(1)请将折线统计图补充完整,并直接写出该年级获奖人数最多的班级是 班;
(2)若二班获奖人数占班级参赛人数的32%,则全年级参赛人数是 人;
(3)若该年级并列第一名有男、女同学各2名,从中随机选取2名参加市级比赛,则恰好是1男1女的概率是 .
( http: / / www.21cnjy.com )
五练原创——预测提升
1、在一次科技作品制作比赛中,某小组八 ( http: / / www.21cnjy.com )件作品的成绩(单位:分)分别是7,10,9,8,7,9,9,8,对这组数据,下列说法正确的是( )
A. 中位数是8 B. 众数是9 C. 平均数是8 D. 极差是7
2、如图是小芹6月1日﹣7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
( http: / / www.21cnjy.com )
A. 1小时 B. 1.5小时 C. 2小时 D. 3小时
3、下列说法正确的是( )
A. 必然事件发生的概率为0
B. 一组数据1,6,3,9,8的极差为7
C. “面积相等的两个三角形全等”这一事件是必然事件
D. “任意一个三角形的外角和等于180°”这一事件是不可能事件
4、小洁的妈妈经营的玩具店进了一纸箱除 ( http: / / www.21cnjy.com )颜色外都相同的散装塑料球共1000个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,把它放回纸箱中;…多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱内红球的个数约是 个.
5、我市某中学举行了“中国梦 校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,丙绘制了不完整的两种统计图.
( http: / / www.21cnjy.com )
根据图中提供的信息,回答下列问题:
(1)参加演讲比赛的学生共有 人,并把条形图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形的圆心角为 度;
(3)学校欲从或A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求或A等级的小明参加市比赛的概率.
6、在一个口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.小明和小强采取了不同的摸取方法,分别是:
小明:随机抽取一个小球记下标号,然后放回,再随机地摸取一个小球,记下标号;
小强:随机摸取一个小球记下标号,不放回,再随机地抽取一个小球,记下标号.
(1)用画树状图(或列表法)分别表示小明和小强摸球的所有可能出现的结果;
(2)分别求出小明和小强两次摸球的标号之和等于5的概率.
第一篇 专题整合篇
专题12 统计与概率(讲案)
一讲考点——考点梳理
总体与样本
1.我们考察的对象一般是具体问题里的某种数量指标,也就是说,总体实质上是一些”数“的总体,而不是”物“的全体
2.样本中个体的数目叫样本容量,样本是由有限的一部分个体组成,样本的容量是正整数(没有单位)
(二)频数分布直方图
1.条形图和直方图的区别
(1)条形图是用条形的高度表示频数的大小,而直方图实际上是用长方形的面积表示频
(2)条形图中,横轴上的数据是孤立的,是一个具体的数据,而直方图中,横轴上的数据是连续的,是一个范围.
(3)条形图中,各长方形之间有空隙,而直方图中,各长方形是靠在一起的.
2.与频数.频数相关的公式
(1)频数=频率×总数.
(2)各组频数之和等于总数.
(3)各组频率之和等于1
(三)事件类型
事件类型 定义 举例 概率
确定事件 必然事件 一定会发生的事件 “投一枚骰子,出现的点数大于0”是必然事件 1
不可能事件 一定不会发生的事件 “投一枚骰子,出现的点数是7”是不可能事件 0
随机事件 可能发生也可能不发生的事件 “抛投一枚硬币,出现正面朝上”是随机事件 0~1之间
(四)方差
1.方差和极差都能表示一组数据的离散程度.极差表示一组数据的变化范围,方差表示一组数据的波动大小.
2.极差大只能说明这组数据中最大值与最小值的离散程度大小,但不能表示其他数据的波动大小,即极差不能准确地衡量数据的波动程度.
3.在样本容量相同的情况下,方差越大,说明数据波动越大,越不稳定;方差越小,说明数据波动越小,越稳定.
(五)概率
1.概率公式:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=.
2.用频率估计概率
一般地,在大量重复试验中,如果事件A发生的频率n分之m会稳定在某个常数p附近,那么事件A发生的概率P(A)=p.
二讲题型——题型解析
(一)统计图的综合应用
例1 近期国家颁布禁令,禁止在公共场合吸烟。禁令颁布后,小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:
A.顾客出面制止;
B.劝说到室外吸烟;
C.餐厅工作人员出面制止;
D.无所谓.
他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
( http: / / www.21cnjy.com )
(1)这次抽样调查的人数有 人;
(2)请将统计图①补充完整;
(3)在统计图②中,“无所谓”部分所对应的圆心角是 度;
(4)若城区人口有400万人,估计赞成“餐厅工作人员出面制止”的有多少万人?
(二)众数、中位数、平均数
例2 某校初中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球共投10次.甲、乙两名同学测试情况如图所示:
( http: / / www.21cnjy.com )
根据图中所提供的信息解答下列问题;
(1)读图填表:
甲每次投中的个数
乙每次投中的个数
(2)写出甲、乙两人投篮个数的众数和中位数;
(3)求出两人投篮个数的平均数.
(三)数据的波动:方差
例3 有关部门从甲、乙两个城市所有的自动售货机中分别随机抽取了16台,记录下某一天各自的销售情况(单位:元):
甲:l8, 8,10,43, 5,30,10,22, 6,27,25,58,14,18,30,41
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,l0,34,23
小强用如图所示的方法表示甲城市16台自动售货机的销售情况.
( http: / / www.21cnjy.com )
(1)请你仿照小强的方法将乙城市16台自动售货机的销售情况表示出来;
(2)用不等号填空:甲_____乙;s_____s;
(3)请说出此种表示方法的优点.
(四)概率公式
例4 一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程有两个不相等实数根的概率.
(五)概率中的放回与不放回问题
例5 在一个不透明的布口袋中装有只有颜色不同,其他都相同的白、红、黑三种颜色的小球各只,甲、乙两人进行摸球游戏:甲先从袋中摸出一球,看清颜色后放回,再由乙从袋中摸出一球.
(1)试用树状图(或列表法)表示摸球游戏所有可能的结果;
(2)如果规定:乙摸到与甲相同颜色的球为乙胜,否则为甲胜,问谁在游戏中获胜的可能性更大些?
(六)游戏中的概率问题
例6 一个不透明的口袋中装有4个完全相同 ( http: / / www.21cnjy.com )的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
( http: / / www.21cnjy.com )
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
三讲方法——方法点睛
1.样本的几点说明:(1)样本的提取是否得 ( http: / / www.21cnjy.com )当直接关系到对总体估计的准确度,因此为了获得较准确的调查结果,抽取的样本要具有代表性和广泛性.(2)总体和样本的关系:总体包括所有个体,样本只包含一部分个体.样本是总体的一部分,总体可以有多个样本,一个样本在一定程度上反映总体.(3)样本容量是样本中个体的数目.一般的,样本容量越大,通过样本对总体的估计越准确.在实际情况中,要根据具体情况确定样本容量的大小.
2.统计图的分析有:条形统计图、扇形统计图 ( http: / / www.21cnjy.com )、折线统计图三种,条形统计图能清晰地显示每组数据的具体值,折线统计图能确切地表示出各部分的具体值,还能显示出各个数据的变化趋势;扇形统计图能够清楚地表示各部分在总体中所占的百分比.
3.众数、中位数
众数是指一组数据中出现次数 ( http: / / www.21cnjy.com )最多的数,它可以有多个;中位数是指将一组数据按从大到小(或从小到大)的顺序排列后,位于最中间的一个数或两个数的平均数,计算时要分清是奇数个还是偶数个.
4.平均数
一组数据的平均数是,若所占的权分别是,则加权平均数是.
5. 常见的求概率的方法
(1).列举法
在一次实验中,如果可能出现的结果只有有 ( http: / / www.21cnjy.com )限个,且各种结果出现的可能性大小相等,我们可以通过列举试验结果的方法,分析出随机事件发生的概率,这种方法称为列举法.
(2).画树状图法
通过画树状图列出列出某事件的所有可 ( http: / / www.21cnjy.com )能的结果,求出其概率的方法叫做树状图法.当一次试验要涉及三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果, 通常采用树状图法求概率.
(3).列表法
用列出表格的方法来分析和求解某些事 ( http: / / www.21cnjy.com )件的概率的方法叫做列表法.当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.
四练实题——随堂小练
1、下列说法正确的是( )
A. 了解某班同学的身高情况适合用全面调查
B. 数据2、3、4、2、3的众数是2
C. 数据4、5、5、6、0的平均数是5
D. 甲、乙两组数据的平均数相同,方差分别是,则甲组数据更稳定
2、在市教育局举行的“经典诗朗诵”演讲比赛中 ( http: / / www.21cnjy.com ),有11名学生参加决赛,他们决赛的成绩各不相同,其中的一名学生想知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
3、一个袋中只装有3个红球,从中随机摸出一个是红球( )
A. 可能性为 B. 属于不可能事件 C. 属于随机事件 D. 属于必然事件
4、甲、乙、丙三位同学打乒 ( http: / / www.21cnjy.com )乓球,想通过“手心手背”游戏来决定其中哪两个人先打,规则如下:三个人同时各用一只手随机出示手心或手背,若只有两个人手势相同(都是手心或都是手背),则这两人先打,若三人手势相同,则重新决定.那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是 .
5、把形状、大小、质地完全相同的4张卡片分别标上数字﹣1、﹣4、0、2,将这4张卡片放入不透明的盒子中搅匀.求下列事件的概率:
(1)从中随机抽取一张卡片,卡片上的数字是负数;
(2)先从盒子中随机抽取一张卡片不放回,再随机抽取一张,两张卡片上的数字之积为0(用列表法或树形图).
6、某中学组织网络安全知 ( http: / / www.21cnjy.com )识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
(1)请将折线统计图补充完整,并直接写出该年级获奖人数最多的班级是 班;
(2)若二班获奖人数占班级参赛人数的32%,则全年级参赛人数是 人;
(3)若该年级并列第一名有男、女同学各2名,从中随机选取2名参加市级比赛,则恰好是1男1女的概率是 .
( http: / / www.21cnjy.com )
五练原创——预测提升
1、在一次科技作品制作比赛中,某小组八 ( http: / / www.21cnjy.com )件作品的成绩(单位:分)分别是7,10,9,8,7,9,9,8,对这组数据,下列说法正确的是( )
A. 中位数是8 B. 众数是9 C. 平均数是8 D. 极差是7
2、如图是小芹6月1日﹣7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
( http: / / www.21cnjy.com )
A. 1小时 B. 1.5小时 C. 2小时 D. 3小时
3、下列说法正确的是( )
A. 必然事件发生的概率为0
B. 一组数据1,6,3,9,8的极差为7
C. “面积相等的两个三角形全等”这一事件是必然事件
D. “任意一个三角形的外角和等于180°”这一事件是不可能事件
4、小洁的妈妈经营的玩具店进了一纸箱除 ( http: / / www.21cnjy.com )颜色外都相同的散装塑料球共1000个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,把它放回纸箱中;…多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱内红球的个数约是 个.
5、我市某中学举行了“中国梦 校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,丙绘制了不完整的两种统计图.
( http: / / www.21cnjy.com )
根据图中提供的信息,回答下列问题:
(1)参加演讲比赛的学生共有 人,并把条形图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形的圆心角为 度;
(3)学校欲从或A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求或A等级的小明参加市比赛的概率.
6、在一个口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.小明和小强采取了不同的摸取方法,分别是:
小明:随机抽取一个小球记下标号,然后放回,再随机地摸取一个小球,记下标号;
小强:随机摸取一个小球记下标号,不放回,再随机地抽取一个小球,记下标号.
(1)用画树状图(或列表法)分别表示小明和小强摸球的所有可能出现的结果;
(2)分别求出小明和小强两次摸球的标号之和等于5的概率.
同课章节目录
