2015年中考数学二轮专题复习教案:专题06 一次函数、反比例函数的应用
文档属性
| 名称 | 2015年中考数学二轮专题复习教案:专题06 一次函数、反比例函数的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 120.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-05 08:53:38 | ||
图片预览




文档简介
备战2015年中考二轮讲练测
第一篇 专题整合篇
专题06 一次函数与反比例函数的应用(讲案)
一讲考点——考点梳理
1.一次函数的图象和性质:
一次函数的一般形式是____________,图象是经过和两点的一条直线.
一次函数的图象与性质:
k、b的符号 k>0b>0 k>0 b<0 k<0 b>0 k<0b<0
图像的大致位置
经过象限 第 象限 第 象限 第 象限 第 象限
性质 y随x的增大而 y随x的增大而 y随x的增大而 y随x的增大而
2. 求一次函数的解析式的方法是 ,其基本步骤是:
(1)设出函数表达式的一般形式 (2)把 ( http: / / www.21cnjy.com )已知条件代入函数表达式中,得到关于待定系数的方程或方程组 (3)解方程组求出待定系数的值,从而写出函数的表达式
3.一次函数与一元一次方程、一元一次不等式的关系
(1)利用一次函数的图像可以求解不等式的解集,求二元一次方程组的解
(2)利用方程组求一次函数的表达式,利用不等式解决一次函数应用题
4.一次函数的应用
一次函数的应用题主要有:
利用一次函数的图像寻找实际问题中的变化规律解题
利用两个一次函数的图像解决方案选择问题或把问题转化为不等式加以解决
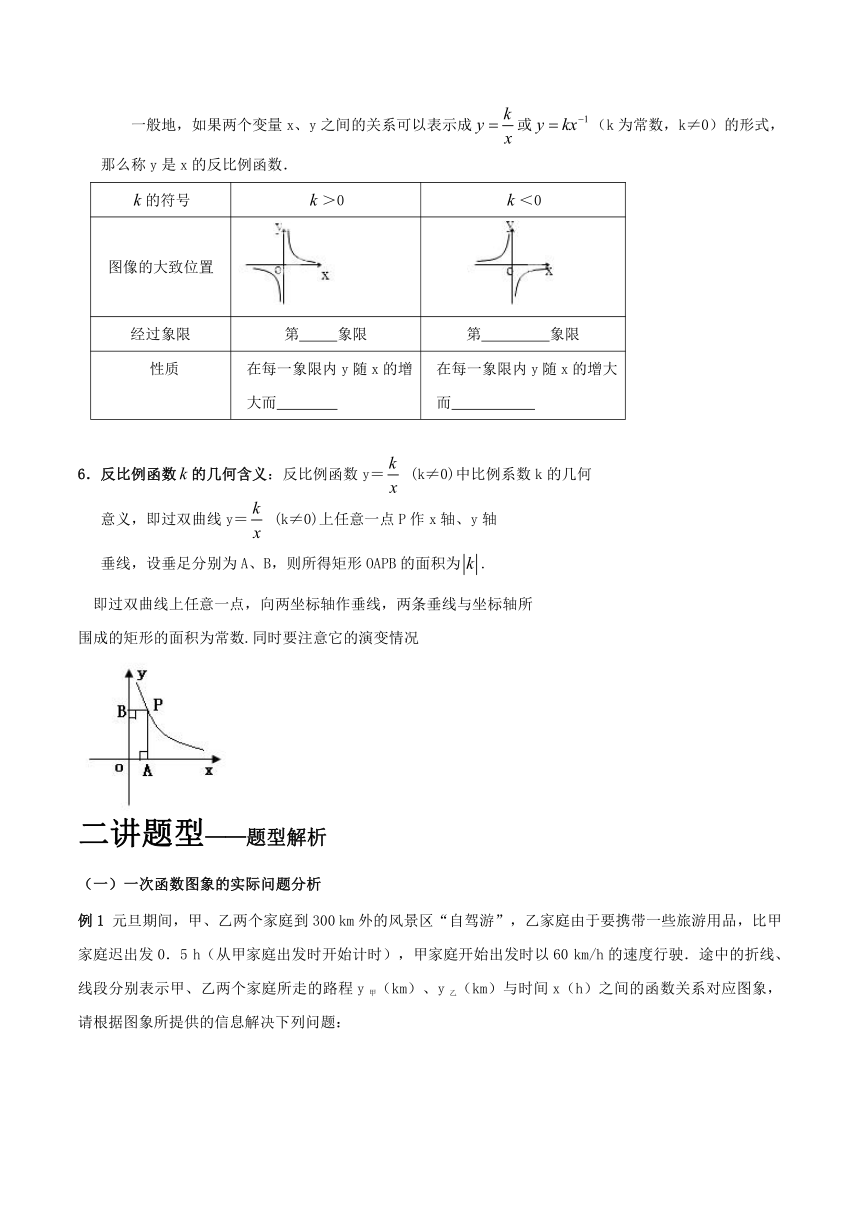
5.反比例函数的图象和性质:
一般地,如果两个变量x、y之间的关系可以表示成或(k为常数,k≠0)的形式,那么称y是x的反比例函数.
的符号 >0 <0
图像的大致位置 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
经过象限 第 象限 第 象限
性质 在每一象限内y随x的增大而 在每一象限内y随x的增大而
6.反比例函数的几何含义:反比例函数y= (k≠0)中比例系数k的几何
意义,即过双曲线y= (k≠0)上任意一点P作x轴、y轴
垂线,设垂足分别为A、B,则所得矩形OAPB的面积为.
即过双曲线上任意一点,向两坐标轴作垂线,两条垂线与坐标轴所
围成的矩形的面积为常数.同时要注意它的演变情况
( http: / / www.21cnjy.com )
二讲题型——题型解析
(一)一次函数图象的实际问题分析
例1 元旦期间,甲、乙两个家庭到300 k ( http: / / www.21cnjy.com )m外的风景区“自驾游”,乙家庭由于要携带一些旅游用品,比甲家庭迟出发0.5 h(从甲家庭出发时开始计时),甲家庭开始出发时以60 km/h的速度行驶.途中的折线、线段分别表示甲、乙两个家庭所走的路程y甲(km)、y乙(km)与时间x(h)之间的函数关系对应图象,请根据图象所提供的信息解决下列问题:
( http: / / www.21cnjy.com )
(1)由于汽车发生故障,甲家庭在途中停留了 h;
(2)甲家庭到达风景区共花了多少时间;
(3)为了能互相照顾,甲、乙两个家庭在第一次相遇后约定两车的距离不超过15 km,请通过计算说明,按图所表示的走法是否符合约定.
(二)一次函数的方案设计问题
例2 学校准备添置一批计算机.
方案1:到商家直接购买,每台需要7000元;
方案2:学校买零部件组装,每台需要6000 ( http: / / www.21cnjy.com )元,另外需要支付安装工工资等其它费用合计3000元.设学校需要计算机x台,方案1与方案2的费用分别为y1、y2元.
(1)分别写出y1、y2的函数解析式;
(2)当学校添置多少台计算机时,两种方案的费用相同?
(3)若学校需要添置计算机50台,那么采用哪一种方案较省钱?说说你的理由
(三)一次函数与方程(组)、不等式的综合应用
例3 2014年白天鹅大酒店按餐厨垃圾处理费25元/吨、建筑垃圾处理费16元/吨的收费标
准,共支付餐厨和建筑垃圾处理费3400元.从2015年元月起,收费标准上调为:餐厨垃圾处理费100元/
吨,建筑垃圾处理费30元/吨.若该酒店2015年处理的这两种垃圾数量与2014年相比没有变化,就要多
支付垃圾处理费5100元.
(1)该酒店2014年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该酒店计划2015年 ( http: / / www.21cnjy.com )将上述两种垃圾处理总量减少到160吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2015年该酒店最少需要支付这两种垃圾处理费共多少元?
(四)一次函数与几何综合问题
如图,在平面直角坐标系中,已知A(8,0),B(0,6),⊙M经过原点O及点A、B.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)求⊙M的半径及圆心M的坐标;
(2)过点B作⊙M的切线l,求直线l的解析式;
(五)一次函数与反比例函数的综合问题
例5 已知一次函数=ax+b的图象与反比例函数y2= 的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2)
( http: / / www.21cnjy.com )
(1)求两个函数的解析式;
(2)结合图象写出y1<y2时,x的取值范围;
(3)求△AOB的面积;
(4)是否存在一点P,使以点A﹑B﹑O﹑P为顶点的四边形为菱形?若存在,求出顶点P的坐标;若不存在,请说明理由。
(六)反比例函数的应用
例6 为了预防“甲流”,某校对教室采用 ( http: / / www.21cnjy.com )药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量 y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例。现在测得药物8min燃毕,此时室内空气中每立方米含药量6mg,请根据题中所提供信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)药物燃烧时,y关于x的函数关系式 ,
药物燃烧后, y关于x的函数关系式 ;
(2)研究表明,每立方米的含药量不超过1.6mg时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回教室?
三讲方法——方法点睛
1.判断实际问题函数图象的方法:一找起点,二找特殊点,三判断函数图象的变化趋势.
分析函数图象的交点和转折点,说明函数在此点将发生变化,根据函数图象的变化趋势来判断函数的增减性.
2.一次函数、反比例函数解析式的求 ( http: / / www.21cnjy.com )法:在一次函数与反比例函数相交求函数解析式的过程中,通常把交点坐标代入其中一个函数解析式,求得一个字母的值,在利用待定系数法求出另一个函数的解析式.
3.求一次函数和反比例函数的交点: ( http: / / www.21cnjy.com )当一次函数与反比例函数有交点时,通常利用方程思想,联立两个函数解析式,消去y,构造一个关于x的一元二次方程,根据一元二次方程的解法求得x的值,进而得到交点坐标(x,y).
4.利用一次函数解决实际问题的一般步骤:
(1)设定实际问题中的自变量与因变量;
(2)通过待定系数法列方程组求出一次函数的解析式;
(3)利用一元一次不等式(组)确定自变量的取值范围;
(4)利用一次函数的增减性求得实际问题
5.反比例函数的实际应用
反比例函数的图像反映变化规律明显,常利用它的图象找出解决问题的方案
列出函数关系式后,注意自变量的取值范围
注意函数思想、方程思想和不等式思想方法的应用
四练实题——随堂小练
1.“黄金1号”玉米种子的价格为5元/千克, ( http: / / www.21cnjy.com )如果一次购买2千克以上的种子,超过2千克部分的种子价格打6折,设购买种子数量为x千克,付款金额为y元,则y与x的函数关系的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )
C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A. 1<m<7 B. 3<m<4 C. m>1 D. m<4
3.如图,矩形AOBC中, ( http: / / www.21cnjy.com )顶点C的坐标(4,2),又反比例函数的图像经过矩形的对角线的交点P,则该反比例函数关系式是______________
( http: / / www.21cnjy.com )
4.直线y=kx+b经过点A(-2,0)和y轴负半轴上的一点B,如果△AOB的面积为2,则b的值为 .
( http: / / www.21cnjy.com )
5、甲乙两地相距50千米 ( http: / / www.21cnjy.com ).星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发 小时时,行进中的两车相距8千米.
( http: / / www.21cnjy.com )
6、如图,在△AOB中,∠ABO=90 ( http: / / www.21cnjy.com )°,OB=4,AB=8,反比例函数在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积为4.
(1)求反比例函数解析式;
(2)求点C的坐标.
( http: / / www.21cnjy.com )
五练原创——预测提升
1. 已知如图,一次函数y=ax+b和反比例函数的图象相交于A、B两点,不等式ax+b>的解集为( )
( http: / / www.21cnjy.com )
A. x<﹣3 B. ﹣3<x<0或x>1 C. x<﹣3或x>1 D. ﹣3<x<1
2. 小明从家出发,外出散步,到一个公 ( http: / / www.21cnjy.com )共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )
( http: / / www.21cnjy.com )
A. 小明看报用时8分钟 B. 公共阅报栏距小明家200米
C. 小明离家最远的距离为400米 D. 小明从出发到回家共用时16分钟
3. 如图,直线与x轴交于点B,双曲线交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为【 】
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.6
4. 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴上,以OA、OC为边作矩形OABC,双曲线(x>0)交AB于点E,AE:EB=1:3.则矩形OABC的面积是 .
( http: / / www.21cnjy.com )
5. 在一条笔直的公路旁依次有A、 ( http: / / www.21cnjy.com )B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
(1)A、C两村间的距离为 ▲ km,a= ▲ ;
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)乙在行驶过程中,何时距甲10km?
( http: / / www.21cnjy.com )
6.如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
( http: / / www.21cnjy.com )
(1)填空:双曲线的另一支在第 象限,的取值范围是 ;
(2)若点C的坐标为(1,1),请用含有的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
(3)若,,求双曲线的解析式.
第一篇 专题整合篇
专题06 一次函数与反比例函数的应用(讲案)
一讲考点——考点梳理
1.一次函数的图象和性质:
一次函数的一般形式是____________,图象是经过和两点的一条直线.
一次函数的图象与性质:
k、b的符号 k>0b>0 k>0 b<0 k<0 b>0 k<0b<0
图像的大致位置
经过象限 第 象限 第 象限 第 象限 第 象限
性质 y随x的增大而 y随x的增大而 y随x的增大而 y随x的增大而
2. 求一次函数的解析式的方法是 ,其基本步骤是:
(1)设出函数表达式的一般形式 (2)把 ( http: / / www.21cnjy.com )已知条件代入函数表达式中,得到关于待定系数的方程或方程组 (3)解方程组求出待定系数的值,从而写出函数的表达式
3.一次函数与一元一次方程、一元一次不等式的关系
(1)利用一次函数的图像可以求解不等式的解集,求二元一次方程组的解
(2)利用方程组求一次函数的表达式,利用不等式解决一次函数应用题
4.一次函数的应用
一次函数的应用题主要有:
利用一次函数的图像寻找实际问题中的变化规律解题
利用两个一次函数的图像解决方案选择问题或把问题转化为不等式加以解决
5.反比例函数的图象和性质:
一般地,如果两个变量x、y之间的关系可以表示成或(k为常数,k≠0)的形式,那么称y是x的反比例函数.
的符号 >0 <0
图像的大致位置 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
经过象限 第 象限 第 象限
性质 在每一象限内y随x的增大而 在每一象限内y随x的增大而
6.反比例函数的几何含义:反比例函数y= (k≠0)中比例系数k的几何
意义,即过双曲线y= (k≠0)上任意一点P作x轴、y轴
垂线,设垂足分别为A、B,则所得矩形OAPB的面积为.
即过双曲线上任意一点,向两坐标轴作垂线,两条垂线与坐标轴所
围成的矩形的面积为常数.同时要注意它的演变情况
( http: / / www.21cnjy.com )
二讲题型——题型解析
(一)一次函数图象的实际问题分析
例1 元旦期间,甲、乙两个家庭到300 k ( http: / / www.21cnjy.com )m外的风景区“自驾游”,乙家庭由于要携带一些旅游用品,比甲家庭迟出发0.5 h(从甲家庭出发时开始计时),甲家庭开始出发时以60 km/h的速度行驶.途中的折线、线段分别表示甲、乙两个家庭所走的路程y甲(km)、y乙(km)与时间x(h)之间的函数关系对应图象,请根据图象所提供的信息解决下列问题:
( http: / / www.21cnjy.com )
(1)由于汽车发生故障,甲家庭在途中停留了 h;
(2)甲家庭到达风景区共花了多少时间;
(3)为了能互相照顾,甲、乙两个家庭在第一次相遇后约定两车的距离不超过15 km,请通过计算说明,按图所表示的走法是否符合约定.
(二)一次函数的方案设计问题
例2 学校准备添置一批计算机.
方案1:到商家直接购买,每台需要7000元;
方案2:学校买零部件组装,每台需要6000 ( http: / / www.21cnjy.com )元,另外需要支付安装工工资等其它费用合计3000元.设学校需要计算机x台,方案1与方案2的费用分别为y1、y2元.
(1)分别写出y1、y2的函数解析式;
(2)当学校添置多少台计算机时,两种方案的费用相同?
(3)若学校需要添置计算机50台,那么采用哪一种方案较省钱?说说你的理由
(三)一次函数与方程(组)、不等式的综合应用
例3 2014年白天鹅大酒店按餐厨垃圾处理费25元/吨、建筑垃圾处理费16元/吨的收费标
准,共支付餐厨和建筑垃圾处理费3400元.从2015年元月起,收费标准上调为:餐厨垃圾处理费100元/
吨,建筑垃圾处理费30元/吨.若该酒店2015年处理的这两种垃圾数量与2014年相比没有变化,就要多
支付垃圾处理费5100元.
(1)该酒店2014年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该酒店计划2015年 ( http: / / www.21cnjy.com )将上述两种垃圾处理总量减少到160吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2015年该酒店最少需要支付这两种垃圾处理费共多少元?
(四)一次函数与几何综合问题
如图,在平面直角坐标系中,已知A(8,0),B(0,6),⊙M经过原点O及点A、B.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)求⊙M的半径及圆心M的坐标;
(2)过点B作⊙M的切线l,求直线l的解析式;
(五)一次函数与反比例函数的综合问题
例5 已知一次函数=ax+b的图象与反比例函数y2= 的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2)
( http: / / www.21cnjy.com )
(1)求两个函数的解析式;
(2)结合图象写出y1<y2时,x的取值范围;
(3)求△AOB的面积;
(4)是否存在一点P,使以点A﹑B﹑O﹑P为顶点的四边形为菱形?若存在,求出顶点P的坐标;若不存在,请说明理由。
(六)反比例函数的应用
例6 为了预防“甲流”,某校对教室采用 ( http: / / www.21cnjy.com )药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量 y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例。现在测得药物8min燃毕,此时室内空气中每立方米含药量6mg,请根据题中所提供信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)药物燃烧时,y关于x的函数关系式 ,
药物燃烧后, y关于x的函数关系式 ;
(2)研究表明,每立方米的含药量不超过1.6mg时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回教室?
三讲方法——方法点睛
1.判断实际问题函数图象的方法:一找起点,二找特殊点,三判断函数图象的变化趋势.
分析函数图象的交点和转折点,说明函数在此点将发生变化,根据函数图象的变化趋势来判断函数的增减性.
2.一次函数、反比例函数解析式的求 ( http: / / www.21cnjy.com )法:在一次函数与反比例函数相交求函数解析式的过程中,通常把交点坐标代入其中一个函数解析式,求得一个字母的值,在利用待定系数法求出另一个函数的解析式.
3.求一次函数和反比例函数的交点: ( http: / / www.21cnjy.com )当一次函数与反比例函数有交点时,通常利用方程思想,联立两个函数解析式,消去y,构造一个关于x的一元二次方程,根据一元二次方程的解法求得x的值,进而得到交点坐标(x,y).
4.利用一次函数解决实际问题的一般步骤:
(1)设定实际问题中的自变量与因变量;
(2)通过待定系数法列方程组求出一次函数的解析式;
(3)利用一元一次不等式(组)确定自变量的取值范围;
(4)利用一次函数的增减性求得实际问题
5.反比例函数的实际应用
反比例函数的图像反映变化规律明显,常利用它的图象找出解决问题的方案
列出函数关系式后,注意自变量的取值范围
注意函数思想、方程思想和不等式思想方法的应用
四练实题——随堂小练
1.“黄金1号”玉米种子的价格为5元/千克, ( http: / / www.21cnjy.com )如果一次购买2千克以上的种子,超过2千克部分的种子价格打6折,设购买种子数量为x千克,付款金额为y元,则y与x的函数关系的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com )
C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.把直线y=﹣x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A. 1<m<7 B. 3<m<4 C. m>1 D. m<4
3.如图,矩形AOBC中, ( http: / / www.21cnjy.com )顶点C的坐标(4,2),又反比例函数的图像经过矩形的对角线的交点P,则该反比例函数关系式是______________
( http: / / www.21cnjy.com )
4.直线y=kx+b经过点A(-2,0)和y轴负半轴上的一点B,如果△AOB的面积为2,则b的值为 .
( http: / / www.21cnjy.com )
5、甲乙两地相距50千米 ( http: / / www.21cnjy.com ).星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发 小时时,行进中的两车相距8千米.
( http: / / www.21cnjy.com )
6、如图,在△AOB中,∠ABO=90 ( http: / / www.21cnjy.com )°,OB=4,AB=8,反比例函数在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积为4.
(1)求反比例函数解析式;
(2)求点C的坐标.
( http: / / www.21cnjy.com )
五练原创——预测提升
1. 已知如图,一次函数y=ax+b和反比例函数的图象相交于A、B两点,不等式ax+b>的解集为( )
( http: / / www.21cnjy.com )
A. x<﹣3 B. ﹣3<x<0或x>1 C. x<﹣3或x>1 D. ﹣3<x<1
2. 小明从家出发,外出散步,到一个公 ( http: / / www.21cnjy.com )共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )
( http: / / www.21cnjy.com )
A. 小明看报用时8分钟 B. 公共阅报栏距小明家200米
C. 小明离家最远的距离为400米 D. 小明从出发到回家共用时16分钟
3. 如图,直线与x轴交于点B,双曲线交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为【 】
( http: / / www.21cnjy.com )
A.2 B.3 C.4 D.6
4. 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴上,以OA、OC为边作矩形OABC,双曲线(x>0)交AB于点E,AE:EB=1:3.则矩形OABC的面积是 .
( http: / / www.21cnjy.com )
5. 在一条笔直的公路旁依次有A、 ( http: / / www.21cnjy.com )B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
(1)A、C两村间的距离为 ▲ km,a= ▲ ;
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)乙在行驶过程中,何时距甲10km?
( http: / / www.21cnjy.com )
6.如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
( http: / / www.21cnjy.com )
(1)填空:双曲线的另一支在第 象限,的取值范围是 ;
(2)若点C的坐标为(1,1),请用含有的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
(3)若,,求双曲线的解析式.
同课章节目录
