15。1 整式的乘法复习(1)
文档属性
| 名称 | 15。1 整式的乘法复习(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 683.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-11 00:00:00 | ||
图片预览








文档简介
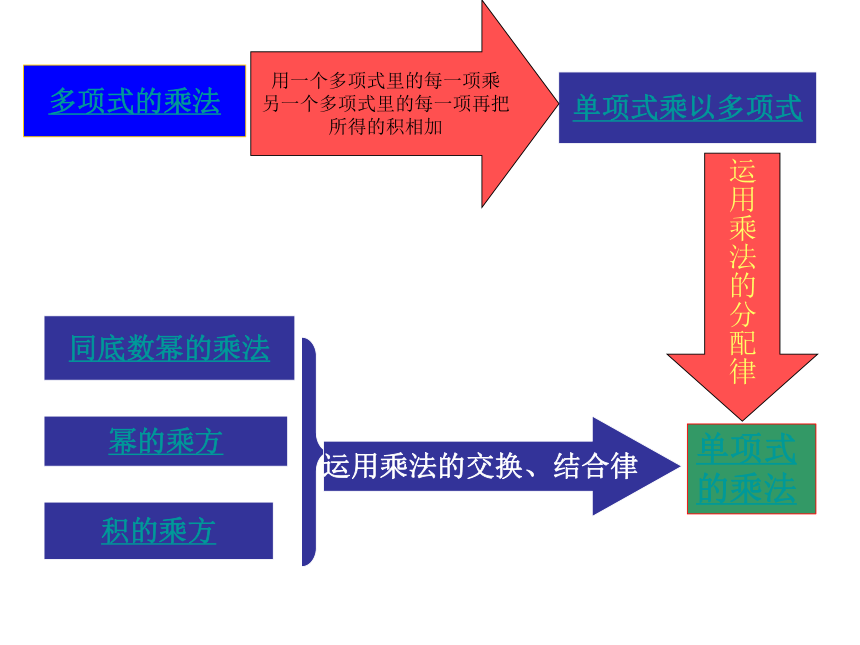
课件26张PPT。15.1 整式的复习(1)南门学校八年(1)(2)班单项式的乘法单项式乘以多项式运用乘法的分配律多项式的乘法用一个多项式里的每一项乘
另一个多项式里的每一项再把
所得的积相加 同底数幂的乘法:底数不变,指数相加即:am·an=a m+n(m、n都是正整数)幂的乘方底数不变,指数相乘即:(a m)n = a mn (m,n都是正整数)积的乘方积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘。即:(ab) n = a n b n (n为正整数)同底数幂的乘法:底数不变,指数相加即:am·an=a m+n(m、n都是正整数)比一比,看谁做的快又对填空:
(1)x·x2= ; (2)x3·x2·x= ;
?(3)a2·a5= ; (4)y5·y4·y3= ;
?(5)m6·m6= ; (6)10·102·105= ;
(7)x2·x3+x·x4= ; (8)y4·y+y·y·y3= ;
x3x6a7y12m121082x52y5看一看,谁能做的最正确
(1)103×100×10+100×100×100- 10000×10×10
(2)(x+y)2·(x+y)5 (3) (x-y)5·(x-y)·(x-y)6
(4)(x-y)5·(x-y)3·(x-y)5 (5)(s+t)·(s+t)2·(s+t)3·(s+t)4
(6)?(a+b-c)3·(c-a-b)3
(7)(a-b-c)·(b+c-a)2·(c-a+b)
.(8) x·x m-1+x2·x m-2-3·x3·x m-3
=106=(x+y)7=(x-y)12=(x-y)13=(s+t)10=-(a+b-c)6=-(a-b-c)4=-x m幂的乘方底数不变,指数相乘即:(a m)n = a mn (m,n都是正整数)再回首2、填空:
(1)(103)2= ;(2)(x3)4= ;
?(3)(-x3)5= ;(4)(-x5)3= ;
?(5)(-x2)3= ;(6)(-x)2= .
106x12-x15-x15-x6x2积的乘方积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘。即:(ab) n = a n b n (n为正整数)练一练 (1)x30=x3· =(x3· )2=[x·(-x3)· ( )3]3;
?(2)若xn=3,yn=2,则(xy)n= ,(x2y3)n= ;
?(3)若1284·83=2n,则n= ;
?(4)若2 x+3·3 x+3=36 x-2,则x= ;
?(5)若x3n=-2,则x9n= ;
?(6)若10x=2,10y=3,则10 2x+3y= .
?
x27x12-x2672137-8108即:(a m)n = a mn (m,n都是正整数)做一做1、计算:[-(a2)3]2·(ab2)3·(-2ab)
?2、(a2)3·(b3)2·(ab)4=
3、若x2n=5,求(x3n)2- (x2)2n的值.
4、已知4x=2 3x-1,求x的值。
5、已知a2n=3,a3m=2,求a 6n+9m的值。
6、若a2n=5,则2a6n-4= .
7、0.1252008×(-8)2009= .
?8、-2a16b7100X=1216a10b10246-8单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。单项式乘以单项式法则:(1)系数相乘(2)相同字母的幂相乘(3)其余字母连同它的指数不变,
作为积的因式。熟能生巧计算:1、(3a2b3)2·(- 2ab3c)2
2
解:原式=(9a4b6) (4a2b6c2)
=(9×4)(a4·a2) (b6·b6) ·c2
=36a6b12c2=24(a – b)43·· 单项式与多项式相乘法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。m(a+b+c)=ma+mb+mc试一试1、2x2·(x2+3xy-y2) – xy(6x2 –4y2)+y2(2x2 – 4xy + y2)
2、an(an + a n - 1 – 3)2x4 +y4答案:a2n + a 2n – 1 – 3an多项式的乘法法则 多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.(a+b)(m+n)=am+an+bm+bn1234练一练1、化简:
(2x2-1)(x2+2)-(2x2+3)(x2-2)
?2、化简:
(x-1)(x-2)+(2x-1)(x+5)-(x-5)(x+3)
?14、先化简,再求值:
(3a+1)(2a-3)-6(a+2)(a-1),其中a=-3
?
4x2+42x2+8x+1238动动脑,提能力1、31000的末位数是 .2、a 2n+1· =a 3n+4.
3、(xm·xm+x m+2·x m-2+x m+n·x m-n)2
4、(-1.2×102) ×(5×103) ×(2×104)
5、解方程:2x(x-1)-x(3x+2)=-x(x-2)-12;
.
?
?
1a n+39x 4m7.2×1010X = 2想
一
想下列各题错在哪里?··41123找一找下列各式中运算正确的是( )(A)(D)(B)(C)D6n口答练习(1)(3)(7)(5)(4)(2)7比一比算
计(1)( )-2b2a+2b( )-2ab(a-b)其中a=1,b=21.拓展训练
(5)若n是正整数,且 ,求 的值。挑战自我:2、(-xya) · nx2y2= 6x3y4 则 n = __, a = __-623、若(am+1bn+2)(a2n-1b2m)=a5b3 则m+n的值为 ( )(A) 1 (B)2 (C)3 (D) -3 BB (1)x30=x3· =(x3· )2=[x·(-x3)· ( )3]3;
?(2)若xn=3,yn=2,则(xy)n= ,(x2y3)n= ;
?(3)若1284·83=2n,则n= ;
?(4)若2 x+3·3 x+3=36 x-2,则x= ;
?(5)若x3n=-2,则x9n= ;
?(6)若10x=2,10y=3,则10 2x+3y= .
?
x27x12-x2672137-8108熟 练 运 用1、计算:[-(a2)3]2·(ab2)3·(-2ab)
?2、(a2)3·(b3)2·(ab)4=
3、若x2n=5,求(x3n)2- (x2)2n的值.
4、已知4x=2 3x-1,求x的值。
5、已知a2n=3,a3m=2,求a 6n+9m的值。
6、若a2n=5,则2a6n-4= .
7、0.1252008×(-8)2009= .
?8、-2a16b7100X=1216a10b10246-8熟 练 运 用再见
另一个多项式里的每一项再把
所得的积相加 同底数幂的乘法:底数不变,指数相加即:am·an=a m+n(m、n都是正整数)幂的乘方底数不变,指数相乘即:(a m)n = a mn (m,n都是正整数)积的乘方积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘。即:(ab) n = a n b n (n为正整数)同底数幂的乘法:底数不变,指数相加即:am·an=a m+n(m、n都是正整数)比一比,看谁做的快又对填空:
(1)x·x2= ; (2)x3·x2·x= ;
?(3)a2·a5= ; (4)y5·y4·y3= ;
?(5)m6·m6= ; (6)10·102·105= ;
(7)x2·x3+x·x4= ; (8)y4·y+y·y·y3= ;
x3x6a7y12m121082x52y5看一看,谁能做的最正确
(1)103×100×10+100×100×100- 10000×10×10
(2)(x+y)2·(x+y)5 (3) (x-y)5·(x-y)·(x-y)6
(4)(x-y)5·(x-y)3·(x-y)5 (5)(s+t)·(s+t)2·(s+t)3·(s+t)4
(6)?(a+b-c)3·(c-a-b)3
(7)(a-b-c)·(b+c-a)2·(c-a+b)
.(8) x·x m-1+x2·x m-2-3·x3·x m-3
=106=(x+y)7=(x-y)12=(x-y)13=(s+t)10=-(a+b-c)6=-(a-b-c)4=-x m幂的乘方底数不变,指数相乘即:(a m)n = a mn (m,n都是正整数)再回首2、填空:
(1)(103)2= ;(2)(x3)4= ;
?(3)(-x3)5= ;(4)(-x5)3= ;
?(5)(-x2)3= ;(6)(-x)2= .
106x12-x15-x15-x6x2积的乘方积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘。即:(ab) n = a n b n (n为正整数)练一练 (1)x30=x3· =(x3· )2=[x·(-x3)· ( )3]3;
?(2)若xn=3,yn=2,则(xy)n= ,(x2y3)n= ;
?(3)若1284·83=2n,则n= ;
?(4)若2 x+3·3 x+3=36 x-2,则x= ;
?(5)若x3n=-2,则x9n= ;
?(6)若10x=2,10y=3,则10 2x+3y= .
?
x27x12-x2672137-8108即:(a m)n = a mn (m,n都是正整数)做一做1、计算:[-(a2)3]2·(ab2)3·(-2ab)
?2、(a2)3·(b3)2·(ab)4=
3、若x2n=5,求(x3n)2- (x2)2n的值.
4、已知4x=2 3x-1,求x的值。
5、已知a2n=3,a3m=2,求a 6n+9m的值。
6、若a2n=5,则2a6n-4= .
7、0.1252008×(-8)2009= .
?8、-2a16b7100X=1216a10b10246-8单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。单项式乘以单项式法则:(1)系数相乘(2)相同字母的幂相乘(3)其余字母连同它的指数不变,
作为积的因式。熟能生巧计算:1、(3a2b3)2·(- 2ab3c)2
2
解:原式=(9a4b6) (4a2b6c2)
=(9×4)(a4·a2) (b6·b6) ·c2
=36a6b12c2=24(a – b)43·· 单项式与多项式相乘法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。m(a+b+c)=ma+mb+mc试一试1、2x2·(x2+3xy-y2) – xy(6x2 –4y2)+y2(2x2 – 4xy + y2)
2、an(an + a n - 1 – 3)2x4 +y4答案:a2n + a 2n – 1 – 3an多项式的乘法法则 多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.(a+b)(m+n)=am+an+bm+bn1234练一练1、化简:
(2x2-1)(x2+2)-(2x2+3)(x2-2)
?2、化简:
(x-1)(x-2)+(2x-1)(x+5)-(x-5)(x+3)
?14、先化简,再求值:
(3a+1)(2a-3)-6(a+2)(a-1),其中a=-3
?
4x2+42x2+8x+1238动动脑,提能力1、31000的末位数是 .2、a 2n+1· =a 3n+4.
3、(xm·xm+x m+2·x m-2+x m+n·x m-n)2
4、(-1.2×102) ×(5×103) ×(2×104)
5、解方程:2x(x-1)-x(3x+2)=-x(x-2)-12;
.
?
?
1a n+39x 4m7.2×1010X = 2想
一
想下列各题错在哪里?··41123找一找下列各式中运算正确的是( )(A)(D)(B)(C)D6n口答练习(1)(3)(7)(5)(4)(2)7比一比算
计(1)( )-2b2a+2b( )-2ab(a-b)其中a=1,b=21.拓展训练
(5)若n是正整数,且 ,求 的值。挑战自我:2、(-xya) · nx2y2= 6x3y4 则 n = __, a = __-623、若(am+1bn+2)(a2n-1b2m)=a5b3 则m+n的值为 ( )(A) 1 (B)2 (C)3 (D) -3 BB (1)x30=x3· =(x3· )2=[x·(-x3)· ( )3]3;
?(2)若xn=3,yn=2,则(xy)n= ,(x2y3)n= ;
?(3)若1284·83=2n,则n= ;
?(4)若2 x+3·3 x+3=36 x-2,则x= ;
?(5)若x3n=-2,则x9n= ;
?(6)若10x=2,10y=3,则10 2x+3y= .
?
x27x12-x2672137-8108熟 练 运 用1、计算:[-(a2)3]2·(ab2)3·(-2ab)
?2、(a2)3·(b3)2·(ab)4=
3、若x2n=5,求(x3n)2- (x2)2n的值.
4、已知4x=2 3x-1,求x的值。
5、已知a2n=3,a3m=2,求a 6n+9m的值。
6、若a2n=5,则2a6n-4= .
7、0.1252008×(-8)2009= .
?8、-2a16b7100X=1216a10b10246-8熟 练 运 用再见
