青岛版数学七年级下册课件8.3.1角的度量 课件 (共14张PPT)
文档属性
| 名称 | 青岛版数学七年级下册课件8.3.1角的度量 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 10:04:56 | ||
图片预览






文档简介
(共14张PPT)
8.3.1角的度量
七年级下册第八单元
1、认识度、分、秒,会进行它们之间的简单换算,会通过角度比较角的大小;
2、会用量角器度量一个角的大小,并判断它是直角、锐角还是钝角.
3.会计算两个角的和、差。
学习目标
重难点:
进行度、分、秒之间的简单换算
回顾旧知
角的读法
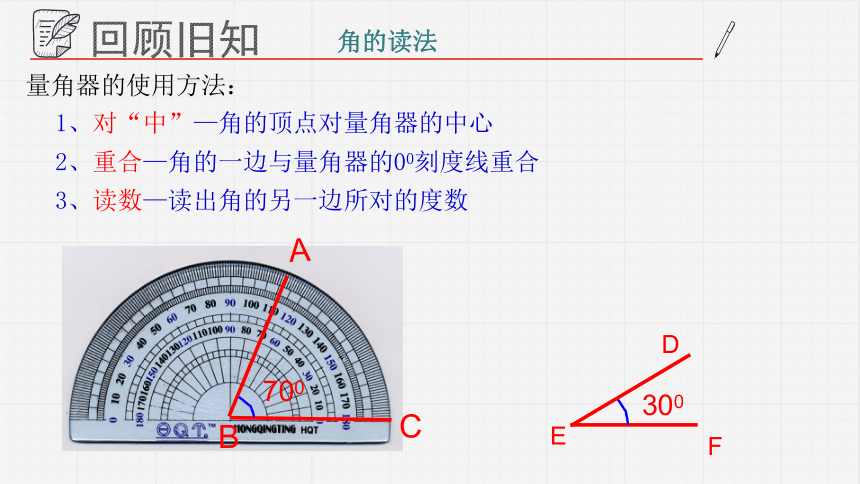
量角器的使用方法:
1、对“中”—角的顶点对量角器的中心
3、读数—读出角的另一边所对的度数
2、重合—角的一边与量角器的00刻度线重合
B
C
A
F
E
D
700
300
观察量角器上的刻度,想一想:1直角等于多少度?1平角等于多少度?并说出锐角和钝角的度数的范围分别是多少?
直角等于90°
平角等于180°
锐角范围是大于0°小于90°
钝角范围是大于90°小于180°
回顾旧知
角的度量单位之间的换算:
1°=60′
角的度量单位是度、分、秒,与计量时间的时、分、秒一样,都是六十进制。
探究新知
1′=60″
1°=60 ′=3600 ″
例如:48 °= 2880′
它们之间的转化方法:由高级单位向低级单位转化时用乘法逐级进行;由低级单位向高级单位转化时用除法逐级进行。
度、分、秒之间的互化
(1)度化分、秒
探究新知
(2)分、秒化度
180
3°= ′= ″
10800
20.24°= ° ′
20
14.4
48′= °
0.8
25°36′= °
25.6
45′36″= °
0.76
探究新知
例1: 48°22′13″ 与 48.37°哪个大?
想一想:你还会用其他方法比较这两个角的大小吗?
解:0.37°是用十进制表示的,因此可先将0.37°用分、秒
表示:
0.37°=60′×0.37=22.2′,
0.2′=60″×0.2=12″
∴ 0.37°=22′+0.2′=22′+12″=22′12″
∵ 22′12″<22′13″,
∴ 48.37°< 48°22′13″ .
练习:36°25′与 36.25°哪个大?
即学即练
解: ∵0.25°=0.25×60′=15′
∴36.25°=36°15′
∴36.25°<36°25′
例2:
已知∠α=37°49′ 40″,∠β=52°10′20″
求:(1)∠α+∠β ;(2)∠ β -∠α .
解:
因为∠α=37°49′40″ ,∠β=52°10′20″,所以
(1)∠α +∠β
= 14°20′40″
典型例题
= 37°49′ 40″ + 52°10′20″
=90°
(2)∠β-∠α
= 52°10′20″- 37°49′ 40″
1、顺序:按秒、分、度的次序相加、减。
2、相加时:秒和分满60进1位;
相减时:如需借位,借1°化为60′,借1′化为60″。
即学即练
计算:
(1) 49°38′+66°22′
(2) 180 °- 79°19′
(3) 90°3″ - 57°21′44″
=115°60′
=100°41′
= 89°59′63″-57°21′44″
=(89°-57°)+(59′-21)+(63″-44″)
= 32°+38′ +19″
= 32°38′ 19″
=116°
即学即练
(2)25 °7′30″×5
=(25°×5)+(7′×5)+(30″×5)
= 125°+35′ +150″
= 125°37′ 30″
(二)乘法运算
注意:相乘时,按照乘法分配律进行相乘。
相乘时,秒和分逢60进1位。
(1)38 24′×4
= 38 ×4+24′×4
= 153 36′
4、已知∠AOB=75°18′,∠AOC=27°53′,则∠BOC= 。
巩固应用
1、将下列角的单位由度、分、秒换算成度。
(1)3′36″ (2)22°30′
2、比较32.15°与32°15′的大小。
3、计算:
(1)56°18′+72°48′ (2)131°28′ - 51°32′15″
(3)12°30′20″×2 (4)24°31′×4 - 62°10′
1、由度化为分、秒形式,每次转化需×60;
2、由秒化为分,再由分化为度,每次转化需÷60
角的度数换算----两种方式
角的度数相加、减
1、顺序:按秒、分、度的次序相加、减。
课堂小结
2、相加时:秒和分满60进1位;
相减时:如需借位,借1°化为60′,借1′化为60″。
角的度数相乘
2、相乘时,秒和分逢60进1位。
1、顺序:相乘时,按照乘法分配律进行相乘。
课后作业
作业:
P12练习
同步练习册
8.3.1角的度量
七年级下册第八单元
1、认识度、分、秒,会进行它们之间的简单换算,会通过角度比较角的大小;
2、会用量角器度量一个角的大小,并判断它是直角、锐角还是钝角.
3.会计算两个角的和、差。
学习目标
重难点:
进行度、分、秒之间的简单换算
回顾旧知
角的读法
量角器的使用方法:
1、对“中”—角的顶点对量角器的中心
3、读数—读出角的另一边所对的度数
2、重合—角的一边与量角器的00刻度线重合
B
C
A
F
E
D
700
300
观察量角器上的刻度,想一想:1直角等于多少度?1平角等于多少度?并说出锐角和钝角的度数的范围分别是多少?
直角等于90°
平角等于180°
锐角范围是大于0°小于90°
钝角范围是大于90°小于180°
回顾旧知
角的度量单位之间的换算:
1°=60′
角的度量单位是度、分、秒,与计量时间的时、分、秒一样,都是六十进制。
探究新知
1′=60″
1°=60 ′=3600 ″
例如:48 °= 2880′
它们之间的转化方法:由高级单位向低级单位转化时用乘法逐级进行;由低级单位向高级单位转化时用除法逐级进行。
度、分、秒之间的互化
(1)度化分、秒
探究新知
(2)分、秒化度
180
3°= ′= ″
10800
20.24°= ° ′
20
14.4
48′= °
0.8
25°36′= °
25.6
45′36″= °
0.76
探究新知
例1: 48°22′13″ 与 48.37°哪个大?
想一想:你还会用其他方法比较这两个角的大小吗?
解:0.37°是用十进制表示的,因此可先将0.37°用分、秒
表示:
0.37°=60′×0.37=22.2′,
0.2′=60″×0.2=12″
∴ 0.37°=22′+0.2′=22′+12″=22′12″
∵ 22′12″<22′13″,
∴ 48.37°< 48°22′13″ .
练习:36°25′与 36.25°哪个大?
即学即练
解: ∵0.25°=0.25×60′=15′
∴36.25°=36°15′
∴36.25°<36°25′
例2:
已知∠α=37°49′ 40″,∠β=52°10′20″
求:(1)∠α+∠β ;(2)∠ β -∠α .
解:
因为∠α=37°49′40″ ,∠β=52°10′20″,所以
(1)∠α +∠β
= 14°20′40″
典型例题
= 37°49′ 40″ + 52°10′20″
=90°
(2)∠β-∠α
= 52°10′20″- 37°49′ 40″
1、顺序:按秒、分、度的次序相加、减。
2、相加时:秒和分满60进1位;
相减时:如需借位,借1°化为60′,借1′化为60″。
即学即练
计算:
(1) 49°38′+66°22′
(2) 180 °- 79°19′
(3) 90°3″ - 57°21′44″
=115°60′
=100°41′
= 89°59′63″-57°21′44″
=(89°-57°)+(59′-21)+(63″-44″)
= 32°+38′ +19″
= 32°38′ 19″
=116°
即学即练
(2)25 °7′30″×5
=(25°×5)+(7′×5)+(30″×5)
= 125°+35′ +150″
= 125°37′ 30″
(二)乘法运算
注意:相乘时,按照乘法分配律进行相乘。
相乘时,秒和分逢60进1位。
(1)38 24′×4
= 38 ×4+24′×4
= 153 36′
4、已知∠AOB=75°18′,∠AOC=27°53′,则∠BOC= 。
巩固应用
1、将下列角的单位由度、分、秒换算成度。
(1)3′36″ (2)22°30′
2、比较32.15°与32°15′的大小。
3、计算:
(1)56°18′+72°48′ (2)131°28′ - 51°32′15″
(3)12°30′20″×2 (4)24°31′×4 - 62°10′
1、由度化为分、秒形式,每次转化需×60;
2、由秒化为分,再由分化为度,每次转化需÷60
角的度数换算----两种方式
角的度数相加、减
1、顺序:按秒、分、度的次序相加、减。
课堂小结
2、相加时:秒和分满60进1位;
相减时:如需借位,借1°化为60′,借1′化为60″。
角的度数相乘
2、相乘时,秒和分逢60进1位。
1、顺序:相乘时,按照乘法分配律进行相乘。
课后作业
作业:
P12练习
同步练习册
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
