青岛版数学七年级下册 8.3.2角的度量 课件 (共16张PPT)
文档属性
| 名称 | 青岛版数学七年级下册 8.3.2角的度量 课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 10:38:22 | ||
图片预览





文档简介
(共16张PPT)
8.3.2角的度量
七年级下册第八单元
1.知道两角互余、互补的定义。
2.会用方程的办法求角的度数。
3.会运用余角、补角的性质解决有关的计算和证明问题。
学习目标
重难点:
互余、互补性质的应用。
回顾旧知
1°的60分之一为1分,记作1′,即1°=60′.
1′ 的60分之一为1秒,记作1″,即1′=60″.
1个周角的360分之一是1度的角,记作“1°”.
角的度量单位是什么呢?
平角度数为180°,直角度数为90°
度、分、秒
锐角范围是大于0°小于90°
钝角范围是大于90°小于180°
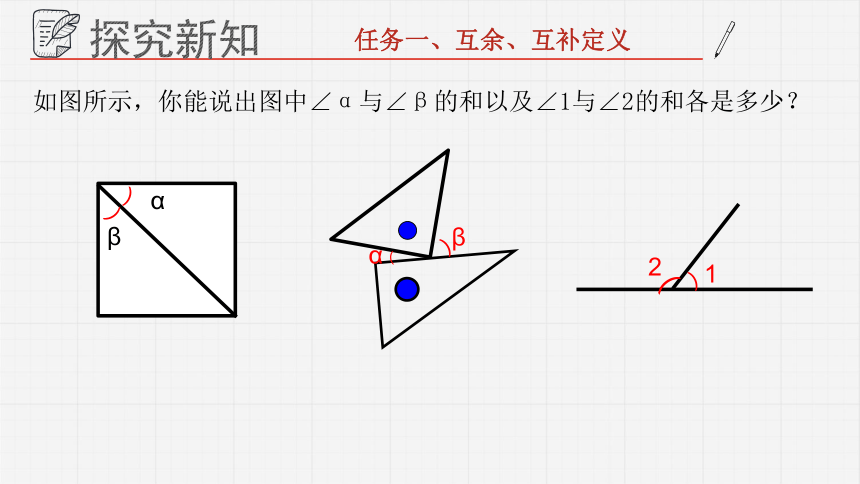
任务一、互余、互补定义
如图所示,你能说出图中∠α与∠β的和以及∠1与∠2的和各是多少?
)
)
α
β
α
β
)
)
1
2
)
)
探究新知
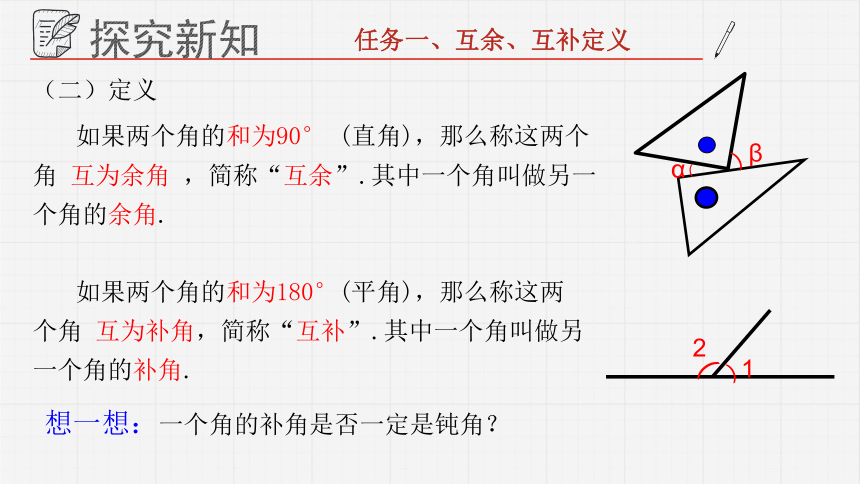
如果两个角的和为90° (直角),那么称这两个角 互为余角 ,简称“互余”.其中一个角叫做另一个角的余角.
如果两个角的和为180°(平角),那么称这两个角 互为补角,简称“互补”.其中一个角叫做另一个角的补角.
α
β
)
)
1
2
)
)
任务一、互余、互补定义
探究新知
(二)定义
想一想:一个角的补角是否一定是钝角?
即学即练
1、在图中找出互余和互补的角
┐
┌
2.帮∠α找朋友
∠α ∠α的余角 ∠α的补角
80°
45°
79°39′
α
10°
45°
10°21′
90°-α
100°
135°
100°21′
180°-α
典型例题
例3:一个角的补角是它的余角的3倍,求这个角的度数?
解:设这个角是 x°,那么它的补角是(180-x) ,余角是(90-x)
根据题意,得
180-x = 3(90-x)
解这个方程,得
x =45.
所以,这个角的度数是 45 .
即学即练
1、(潍坊期中)一个角的余角与这个角的补角之和为130°,求这个角的度数。
2、(聊城期中)已知一个角的补角比它的余角的2倍大45°,求这个角。
70°
45°
探究新知
余角的性质
如图,∠AOC=∠BOD=90°,找出∠3的两个余角,它们相等吗?为什么?与同学交流。
结论:同角的余角相等。
几何语言:∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=∠2
O
A
B
C
D
1
3
2
解:∠3的余角为∠1,∠2。∠1=∠2
∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=90°-∠3
∠2=90°-∠3
∴∠1=∠2
探究新知
余角的性质
如图,∠AOC=∠COE=90°,且∠1=∠3,那么它们的余角相等吗?为什么?
几何语言:
∵∠1+∠2=90°∠3+∠4=90°
且∠1=∠3
∴∠2=∠4
解:相等
A
B
C
D
E
O
1
2
3
4
∵∠1+∠2=90°,∠3+∠4=90°
∴∠2=90°-∠1
∠4=90°-∠3
∵∠1=∠3
∴∠2=∠4
结论:等角的余角相等。
探究新知
补角的性质
如图,直线AB,CD相交于点O,找出∠4的两个补角,它们相等吗?为什么?与同学交流。
几何语言:
∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=∠3
解:∠4的补角为∠1,∠3。∠1=∠3
∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=180°-∠4
∠3=180°-∠4
∴∠1=∠3
结论:同角的补角相等。
1
2
3
4
A
B
C
D
O
探究新知
补角的性质
如图,直线AB,CD相交于点O,∠2=∠4,那么它们的补角相等吗?与同学交流。
几何语言:
∵∠1+∠2=180°,∠3+∠4=180°
且∠2=∠4
∴∠1=∠3
解:相等
∵∠1+∠2=180°
∠3+∠4=180°
∴∠1=180°-∠2
∠3=180°-∠4
∴∠1=∠3
结论:等角的补角相等。
1
2
3
4
A
B
C
D
O
∵∠2=∠4
归纳小结
互余 互补
两角间的数量关系
对应 图形
性质
同角或等角的余角相等
同角或等角的补角相等
∠1+∠2=90°
(∠1=90°-∠2)
∠1+∠2=180°
(∠1=180°-∠2)
巩固应用
1、(聊城期中)已知∠1+∠2=180°且∠2=∠3,则∠3+∠1=180°,依据是( )
A.同角的补角相等 B.等角的补角相等
C.等量代换 D.补角的定义
B
2、∠1与∠2互余,∠1=(6x+8)°,∠2=(4x-8)°,则∠1= ,
∠2= .
解:∵∠1与∠2互余
∴(6x+8)+(4x-8)= 90
x = 9
∴∠1=6×9+8=62°
∠2=4×9-8=28°
62°
28°
课堂小结
1、互余、互补是两角之间的数量关系,只与他们的度数和有关.与位置无关。
2、互余、互补概念中的角是成对出现的。
5、只有锐角才有余角。
3、角α的余角是(90°-α),补角是(180°-α).
4、同一个锐角的补角比余角大90°
6、同角的余角(补角)相等;等角的余角(补角)相等。
课后作业
作业:
P14练习 P15习题8.3
同步练习册
8.3.2角的度量
七年级下册第八单元
1.知道两角互余、互补的定义。
2.会用方程的办法求角的度数。
3.会运用余角、补角的性质解决有关的计算和证明问题。
学习目标
重难点:
互余、互补性质的应用。
回顾旧知
1°的60分之一为1分,记作1′,即1°=60′.
1′ 的60分之一为1秒,记作1″,即1′=60″.
1个周角的360分之一是1度的角,记作“1°”.
角的度量单位是什么呢?
平角度数为180°,直角度数为90°
度、分、秒
锐角范围是大于0°小于90°
钝角范围是大于90°小于180°
任务一、互余、互补定义
如图所示,你能说出图中∠α与∠β的和以及∠1与∠2的和各是多少?
)
)
α
β
α
β
)
)
1
2
)
)
探究新知
如果两个角的和为90° (直角),那么称这两个角 互为余角 ,简称“互余”.其中一个角叫做另一个角的余角.
如果两个角的和为180°(平角),那么称这两个角 互为补角,简称“互补”.其中一个角叫做另一个角的补角.
α
β
)
)
1
2
)
)
任务一、互余、互补定义
探究新知
(二)定义
想一想:一个角的补角是否一定是钝角?
即学即练
1、在图中找出互余和互补的角
┐
┌
2.帮∠α找朋友
∠α ∠α的余角 ∠α的补角
80°
45°
79°39′
α
10°
45°
10°21′
90°-α
100°
135°
100°21′
180°-α
典型例题
例3:一个角的补角是它的余角的3倍,求这个角的度数?
解:设这个角是 x°,那么它的补角是(180-x) ,余角是(90-x)
根据题意,得
180-x = 3(90-x)
解这个方程,得
x =45.
所以,这个角的度数是 45 .
即学即练
1、(潍坊期中)一个角的余角与这个角的补角之和为130°,求这个角的度数。
2、(聊城期中)已知一个角的补角比它的余角的2倍大45°,求这个角。
70°
45°
探究新知
余角的性质
如图,∠AOC=∠BOD=90°,找出∠3的两个余角,它们相等吗?为什么?与同学交流。
结论:同角的余角相等。
几何语言:∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=∠2
O
A
B
C
D
1
3
2
解:∠3的余角为∠1,∠2。∠1=∠2
∵∠1+∠3=90°
∠2+∠3=90°
∴∠1=90°-∠3
∠2=90°-∠3
∴∠1=∠2
探究新知
余角的性质
如图,∠AOC=∠COE=90°,且∠1=∠3,那么它们的余角相等吗?为什么?
几何语言:
∵∠1+∠2=90°∠3+∠4=90°
且∠1=∠3
∴∠2=∠4
解:相等
A
B
C
D
E
O
1
2
3
4
∵∠1+∠2=90°,∠3+∠4=90°
∴∠2=90°-∠1
∠4=90°-∠3
∵∠1=∠3
∴∠2=∠4
结论:等角的余角相等。
探究新知
补角的性质
如图,直线AB,CD相交于点O,找出∠4的两个补角,它们相等吗?为什么?与同学交流。
几何语言:
∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=∠3
解:∠4的补角为∠1,∠3。∠1=∠3
∵∠1+∠4=180°
∠3+∠4=180°
∴∠1=180°-∠4
∠3=180°-∠4
∴∠1=∠3
结论:同角的补角相等。
1
2
3
4
A
B
C
D
O
探究新知
补角的性质
如图,直线AB,CD相交于点O,∠2=∠4,那么它们的补角相等吗?与同学交流。
几何语言:
∵∠1+∠2=180°,∠3+∠4=180°
且∠2=∠4
∴∠1=∠3
解:相等
∵∠1+∠2=180°
∠3+∠4=180°
∴∠1=180°-∠2
∠3=180°-∠4
∴∠1=∠3
结论:等角的补角相等。
1
2
3
4
A
B
C
D
O
∵∠2=∠4
归纳小结
互余 互补
两角间的数量关系
对应 图形
性质
同角或等角的余角相等
同角或等角的补角相等
∠1+∠2=90°
(∠1=90°-∠2)
∠1+∠2=180°
(∠1=180°-∠2)
巩固应用
1、(聊城期中)已知∠1+∠2=180°且∠2=∠3,则∠3+∠1=180°,依据是( )
A.同角的补角相等 B.等角的补角相等
C.等量代换 D.补角的定义
B
2、∠1与∠2互余,∠1=(6x+8)°,∠2=(4x-8)°,则∠1= ,
∠2= .
解:∵∠1与∠2互余
∴(6x+8)+(4x-8)= 90
x = 9
∴∠1=6×9+8=62°
∠2=4×9-8=28°
62°
28°
课堂小结
1、互余、互补是两角之间的数量关系,只与他们的度数和有关.与位置无关。
2、互余、互补概念中的角是成对出现的。
5、只有锐角才有余角。
3、角α的余角是(90°-α),补角是(180°-α).
4、同一个锐角的补角比余角大90°
6、同角的余角(补角)相等;等角的余角(补角)相等。
课后作业
作业:
P14练习 P15习题8.3
同步练习册
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
