青岛版数学七年级下册 8.5垂直 课件 (共21张PPT)
文档属性
| 名称 | 青岛版数学七年级下册 8.5垂直 课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 10:40:10 | ||
图片预览








文档简介
(共21张PPT)
8.5 垂直
七年级下册第八单元
1、理解垂直、垂线、垂线段的概念,会用符号表示两条直线互相垂直.
2、能用三角尺和量角器过一点画已知直线的垂线,掌握过一点有且只
有一条直线与已知直线垂直的性质.
3、了解垂线段的性质,会在图形中画出点到直线的垂线段
4、理解点到直线的距离的意义,能度量点到直线的距离.
学习目标
重难点 掌握过一点有且只有一条直线与已知直线垂直的性质
知识回顾
1、两点之间的距离
两点之间的线段长度叫做两点之间的距离.
2、线段的基本性质
3、直角:
90°的角叫做直角。
两点之间的所有连线中,线段最短,
即两点之间,线段最短.
问题1:两条直线相交可以得到几个角?
知识回顾
问题2:在相交得到的四个角中,下列叙述正确的是:
可能都是锐角
可能都是钝角
可能两个锐角,两个钝角
可能都是直角
如图,直线AB与CD相交于点O,如果∠AOD是直角,图中的其他三个角是什么角?为什么?同学交流。
A
B
C
D
O
垂直的定义及表示
探究新知
(一)探究
两条直线相交所成的四个角中,如果有一个角是直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线 ,它们的交点叫做垂足.
(二)定义
A
B
C
D
O
垂直的定义及表示
探究新知
如图,直线AB与CD互相垂直,O是垂足。
记作:AB⊥CD 或 CD⊥AB
读作:AB垂直于CD或CD垂直于AB.
AB叫做CD的垂线,CD叫做AB的垂线。
(三)几何语言
∵∠COB=90°
∴AB⊥CD
∵AB⊥CD
∴∠COB=90°
例 如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD 的度数.
∴ ∠EOB=90°
A
C
E
B
D
O
1
(
解:
∵ AB⊥OE
∵ ∠BOD =∠1=55°
典型例题
(已知)
(垂直的定义)
(对顶角相等)
∴ ∠EOD =∠EOB +∠BOD
=90°+ 55°
=145°
1、(冠县期中) 有下列几种说法:①两条直线相交所成的四个角中有一个是直角;②两条直线相交所成的四个角相等;③两条直线相交所成的四个角中有一组邻补角相等;④两条直线相交得到的对顶角互补,其中能得到两条直线互相垂直的是( )
A.①③ B.①②③ C.②③④ D.①②③④
D
即学即练
垂线的画法
探究新知
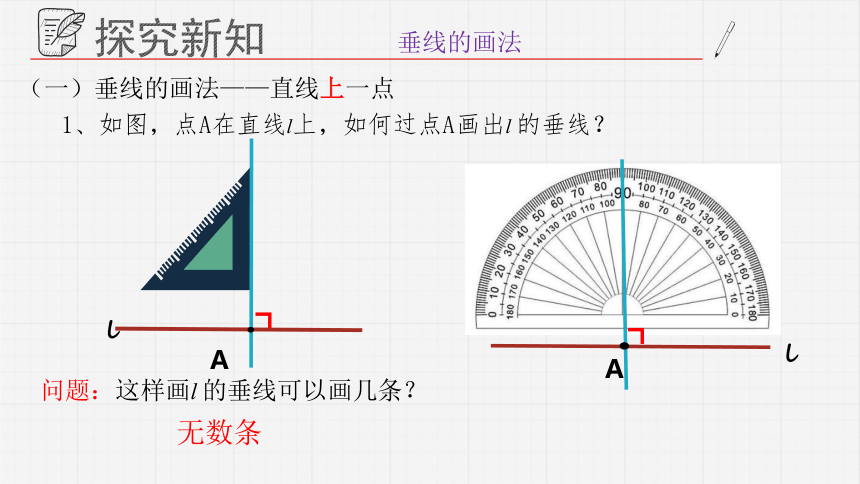
(一)垂线的画法——直线上一点
1、如图,点A在直线l上,如何过点A画出l 的垂线?
┓
A
l
┓
A
l
问题:这样画l 的垂线可以画几条?
无数条
垂线的画法
探究新知
(二)垂线的画法—已知直线 l 和l 上的一点A ,作l 的垂线.
l
A
B
则所画直线AB是过点A的直线l 的垂线.
画垂线的方法
画垂线的方法可归纳为“一落、二过、三画”
1.一落:把三角尺的一条直角边落在已知直线上;
归纳小结
2.二过:让三角尺的另一条直角边经过已知的点
3.三画:沿着直角边经过已知点画直线。
l
A
B
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
垂线的画法
探究新知
(二)垂线的画法—已知直线l 和l 外的一点A ,作l 的垂线.
归纳小结
结论:在同一平面内,过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题: 过直线 l 上(或外)的一点A ,作l 的垂线,可以作几条
思考: 如何用量角器经过直线 l 上(或外)的一点A ,作 l 的垂线 小组交流。
垂线段
探究新知
(一)、垂线性质1
P
l
A
如图所示,点P 是直线 l 外的一点,画PA⊥l,垂足为点A,线段PA 叫做点P 到直线l 的垂线段.
┓
A
l
D
E
C
B
最短的是线段AD
探究新知
垂线段的性质及应用
(二)垂线性质2
在直线l上任取几个点,例如B,C,E,利用圆规比较线段AB,AC,AD,AE的长短,这些线段中哪一条最短?与同学交流。
结论:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成: 垂线段最短.
(垂线性质)
┓
A
l
D
E
C
B
探究新知
垂线段的性质及应用
直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离。
如图,线段AD的长度即点A到直线l的距离。
(三)点到直线的距离
新知应用
思考:如图是一个同学跳远的位置,跳远成绩怎么量
l
P
A
解: 过P点作PA⊥l 于点A,垂线段PA的长度就是该同学的跳远成绩.
新知应用
1、已知:如图AD<AE <AC<AB,能说AD的长是A到BC的距离吗?
D
B
C
A
E
答:不能.
2、已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条
C. 3条 D. 无数条
D
巩固应用
4、如图,∠ABC=90°,∠1=60°,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1=∠2,求∠ABO,∠BOD的度数.
1
2
A
B
C
D
O
)
)
∵BO⊥AC于O点
(已知)
∵∠ABC =90°, ∠1=60°
(已知 )
∴∠ABO =30°
解:
(已知)
∴∠BOC =90°
∴∠BOD=30°
(余角定义)
(余角定义)
(垂直定义)
∵∠2=∠1=60°
课堂小结
3、直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离。
1、在同一平面内,过一点有且只有一条直线与已知直线垂直.
2、连接直线外一点与直线上各点的所有线段中,垂线段最短.
课后作业
作业:
P21练习、 P22习题8.5
同步练习册
8.5 垂直
七年级下册第八单元
1、理解垂直、垂线、垂线段的概念,会用符号表示两条直线互相垂直.
2、能用三角尺和量角器过一点画已知直线的垂线,掌握过一点有且只
有一条直线与已知直线垂直的性质.
3、了解垂线段的性质,会在图形中画出点到直线的垂线段
4、理解点到直线的距离的意义,能度量点到直线的距离.
学习目标
重难点 掌握过一点有且只有一条直线与已知直线垂直的性质
知识回顾
1、两点之间的距离
两点之间的线段长度叫做两点之间的距离.
2、线段的基本性质
3、直角:
90°的角叫做直角。
两点之间的所有连线中,线段最短,
即两点之间,线段最短.
问题1:两条直线相交可以得到几个角?
知识回顾
问题2:在相交得到的四个角中,下列叙述正确的是:
可能都是锐角
可能都是钝角
可能两个锐角,两个钝角
可能都是直角
如图,直线AB与CD相交于点O,如果∠AOD是直角,图中的其他三个角是什么角?为什么?同学交流。
A
B
C
D
O
垂直的定义及表示
探究新知
(一)探究
两条直线相交所成的四个角中,如果有一个角是直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线 ,它们的交点叫做垂足.
(二)定义
A
B
C
D
O
垂直的定义及表示
探究新知
如图,直线AB与CD互相垂直,O是垂足。
记作:AB⊥CD 或 CD⊥AB
读作:AB垂直于CD或CD垂直于AB.
AB叫做CD的垂线,CD叫做AB的垂线。
(三)几何语言
∵∠COB=90°
∴AB⊥CD
∵AB⊥CD
∴∠COB=90°
例 如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD 的度数.
∴ ∠EOB=90°
A
C
E
B
D
O
1
(
解:
∵ AB⊥OE
∵ ∠BOD =∠1=55°
典型例题
(已知)
(垂直的定义)
(对顶角相等)
∴ ∠EOD =∠EOB +∠BOD
=90°+ 55°
=145°
1、(冠县期中) 有下列几种说法:①两条直线相交所成的四个角中有一个是直角;②两条直线相交所成的四个角相等;③两条直线相交所成的四个角中有一组邻补角相等;④两条直线相交得到的对顶角互补,其中能得到两条直线互相垂直的是( )
A.①③ B.①②③ C.②③④ D.①②③④
D
即学即练
垂线的画法
探究新知
(一)垂线的画法——直线上一点
1、如图,点A在直线l上,如何过点A画出l 的垂线?
┓
A
l
┓
A
l
问题:这样画l 的垂线可以画几条?
无数条
垂线的画法
探究新知
(二)垂线的画法—已知直线 l 和l 上的一点A ,作l 的垂线.
l
A
B
则所画直线AB是过点A的直线l 的垂线.
画垂线的方法
画垂线的方法可归纳为“一落、二过、三画”
1.一落:把三角尺的一条直角边落在已知直线上;
归纳小结
2.二过:让三角尺的另一条直角边经过已知的点
3.三画:沿着直角边经过已知点画直线。
l
A
B
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
垂线的画法
探究新知
(二)垂线的画法—已知直线l 和l 外的一点A ,作l 的垂线.
归纳小结
结论:在同一平面内,过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题: 过直线 l 上(或外)的一点A ,作l 的垂线,可以作几条
思考: 如何用量角器经过直线 l 上(或外)的一点A ,作 l 的垂线 小组交流。
垂线段
探究新知
(一)、垂线性质1
P
l
A
如图所示,点P 是直线 l 外的一点,画PA⊥l,垂足为点A,线段PA 叫做点P 到直线l 的垂线段.
┓
A
l
D
E
C
B
最短的是线段AD
探究新知
垂线段的性质及应用
(二)垂线性质2
在直线l上任取几个点,例如B,C,E,利用圆规比较线段AB,AC,AD,AE的长短,这些线段中哪一条最短?与同学交流。
结论:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成: 垂线段最短.
(垂线性质)
┓
A
l
D
E
C
B
探究新知
垂线段的性质及应用
直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离。
如图,线段AD的长度即点A到直线l的距离。
(三)点到直线的距离
新知应用
思考:如图是一个同学跳远的位置,跳远成绩怎么量
l
P
A
解: 过P点作PA⊥l 于点A,垂线段PA的长度就是该同学的跳远成绩.
新知应用
1、已知:如图AD<AE <AC<AB,能说AD的长是A到BC的距离吗?
D
B
C
A
E
答:不能.
2、已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条
C. 3条 D. 无数条
D
巩固应用
4、如图,∠ABC=90°,∠1=60°,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1=∠2,求∠ABO,∠BOD的度数.
1
2
A
B
C
D
O
)
)
∵BO⊥AC于O点
(已知)
∵∠ABC =90°, ∠1=60°
(已知 )
∴∠ABO =30°
解:
(已知)
∴∠BOC =90°
∴∠BOD=30°
(余角定义)
(余角定义)
(垂直定义)
∵∠2=∠1=60°
课堂小结
3、直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离。
1、在同一平面内,过一点有且只有一条直线与已知直线垂直.
2、连接直线外一点与直线上各点的所有线段中,垂线段最短.
课后作业
作业:
P21练习、 P22习题8.5
同步练习册
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
