2024年中考广东专用数学二轮专题复习专题八 圆的综合课件 34张PPT
文档属性
| 名称 | 2024年中考广东专用数学二轮专题复习专题八 圆的综合课件 34张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 16:58:23 | ||
图片预览







文档简介
(共34张PPT)
第二部分 专题复习
专题八 圆的综合
01
基础回顾
02
例题精讲
目录
目录
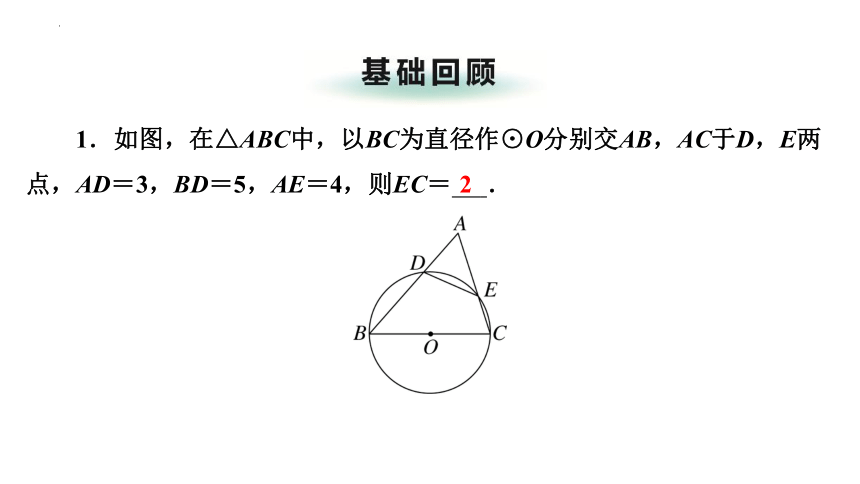
1.如图,在△ABC中,以BC为直径作⊙O分别交AB,AC于D,E两点,AD=3,BD=5,AE=4,则EC= 2 .
2
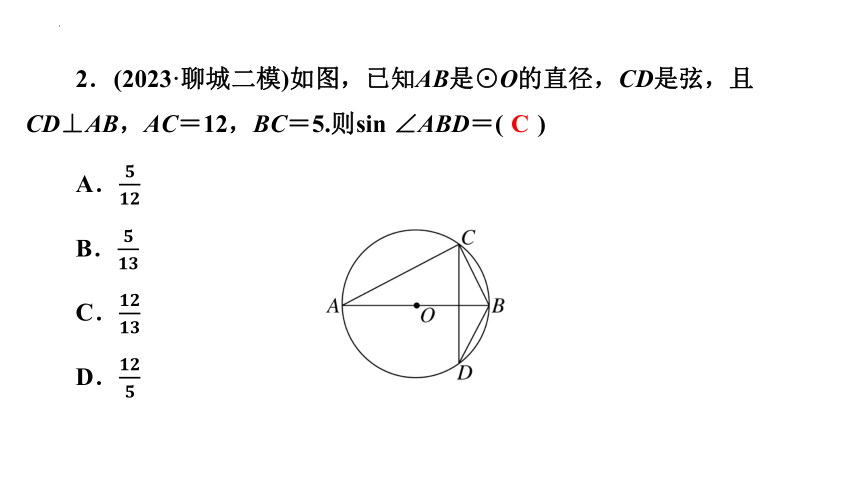
2.(2023·聊城二模)如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=12,BC=5.则sin ∠ABD=( C )
A.
B.
C.
D.
C
如图,AB为⊙O的直径,点D,E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠A.
(1)求证:△ACD∽△DCB;
(1)证明:∵∠C=∠C,∠A=∠BDC,
∴△ACD∽△DCB.
(2)求证:CD是⊙O的切线;
(2)证明:如图,连接OD.
∵AB为⊙O的直径,∴∠ADB=90°.∴∠A+∠ABD=90°.
∵OB=OD,∴∠ABD=∠ODB.
∵∠BDC=∠A,∴∠BDC+∠ODB=90°.
∴∠ODC=90°.∴OD⊥CD.
∵OD是⊙O的半径,∴CD是⊙O的切线.
(3)若tan E=,AC=10,求⊙O的半径.
(3)解:∵∠ADB=90°,tan E=,∠E=∠A,∴tan A==.
由(1),得△DCB∽△ACD.∴===.
∵AC=10,∴=. ∴CD=6.
∴=. ∴BC=. ∴AB=AC-BC=10-=.
∴⊙O的半径为.
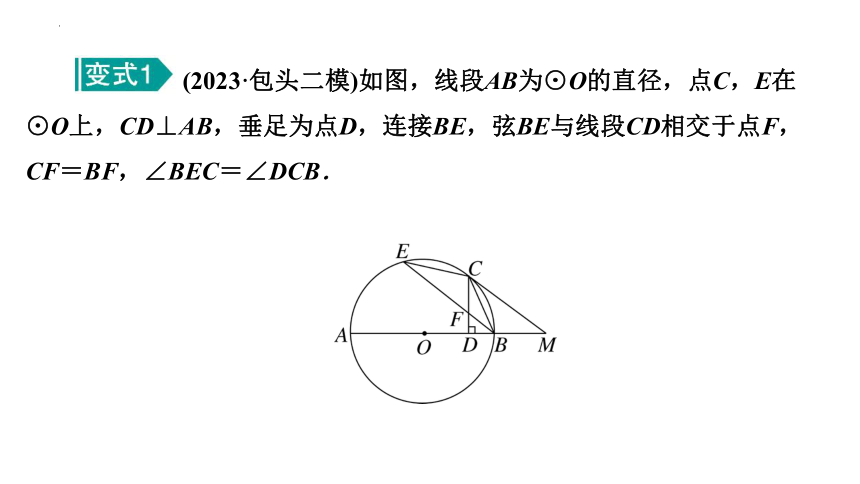
(2023·包头二模)如图,线段AB为⊙O的直径,点C,E在⊙O上,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F,CF=BF,∠BEC=∠DCB.
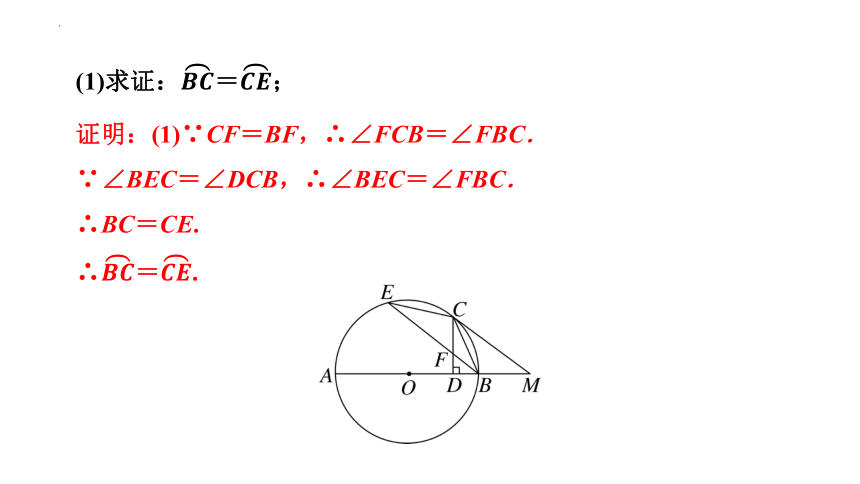
(1)求证:=;
证明:(1)∵CF=BF,∴∠FCB=∠FBC.
∵∠BEC=∠DCB,∴∠BEC=∠FBC.
∴BC=CE.
∴=.
(2)若cos ∠ABE=,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.(用两种证法解答)
(2)法1:如图,连接OC交BE于点H,连接OE.
∵=,∴∠BOC=∠COE.
∵BO=EO,∴OC⊥BE. ∴∠OHB=90°.
在Rt△OBH中,cos ∠OBH==,
∵OB=6,∴BH=×6=.
∴OH===.
∵==,==,∴=.
又∠HOB=∠COM,∴△OHB∽△OCM.
∴∠OCM=∠OHB=90°.∴OC⊥CM.
∵OC是⊙O的半径,∴直线CM是⊙O的切线.
法2:如图,连接AE.
∵AB为⊙O的直径,∴∠AEB=90°.
在Rt△ABE中,cos ∠ABE==,∴cos ∠BAE==.
由(1),得BC=CE.
∴∠COM=∠EOC. ∴∠EAB=∠EOB=∠COM.
∵==,∴=.
∴=. ∴△ABE∽△OMC.
∴∠AEB=∠OCM=90°. ∴OC⊥CM.
∵OC是⊙O的半径,∴直线CM是⊙O的切线.
(2023·温州三模)如图,在△ABC中,AB=AC,⊙O为△ABC的外接圆,弦BD⊥OC于点F,交AC于点E,连接CD.
(1)求证:BE=BC;
(1)证明:∵BD⊥OC,∴=.
∴∠CBE=∠CAB.
又∠ECB=∠BCA,∴△BEC∽△ABC.
∴=.
∵AB=AC,∴BE=BC.
(2)若tan ∠BCA=3,EF=2,求AB的长.
(2)解:由(1),得BE=BC.∴∠BCE=∠BEC.
∵BD⊥OC,tan ∠BCA=3,EF=2,
∴tan ∠BEC===3. ∴CF=6.
∴EC==2.
设BC=BE=x.
∵BC2=BF2+CF2,BF=BE-EF=x-2,
∴x2=(x-2)2+62. 解得x=10. ∴BC=10.
由(1),知△BEC∽△ABC.
∴=,即=. ∴AB=5.
(桂林中考)如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G,交AC于点H.
(1)求证:CD是⊙O的切线;
(1)证明:如图,连接OC.
∵OA=OC,∴∠CAO=∠ACO.
∵AC平分∠DAB,∴∠DAC=∠OAC.
∴∠DAC=∠ACO.∴AD∥OC.
∵CD⊥AD,∴OC⊥CD.
∵OC是⊙O的半径,∴CD是⊙O的切线.
(2)延长AB和DC交于点E,若AE=4BE,求cos ∠DAB的值;
(2)解:∵AE=4BE,OA=OB,设BE=x,则AB=3x.
∴OC=OB=1.5x.∴OE=2.5x.
∵AD∥OC,∴∠COE=∠DAB.
∴cos ∠DAB=cos ∠COE===.
(3)在(2)的条件下,求的值.
(3)解:由(2),知OE=2.5x,OC=1.5x.
∴EC===2x.
∵FG⊥AB,∴∠AGF=90°.
∴∠AFH+∠FAG=90°.
∵∠COE+∠E=90°,∠COE=∠DAB,
∴∠AFH=∠E.
∵∠FAH=∠EAC,∴△AHF∽△ACE.
∴=,即===.
(2023·广东)综合探究
如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A′,连接AA′交BD于点E,连接CA′.
(1)求证:AA′⊥CA′.
(1)证明:∵点A关于BD的对称点为点A′,∴AE=A′E,AA′⊥BD.
∵四边形ABCD是矩形,
∴OA=OC.∴OE∥A′C.
又AA′⊥BD,∴AA′⊥CA′.
(2)以点O为圆心,OE长为半径作圆.
①如图2,⊙O与CD相切,求证:AA′=CA′;
②如图3,⊙O与CA′相切,AD=1,求⊙O的面积.
(2)①证明:如答图1,设⊙O与CD切于点F,连接OF,并延长FO交AB于点G.
∴OF⊥CD,OF=OE.
∵四边形ABCD是矩形,
∴OD=OB=BD,AB∥CD,AC=BD,OA=AC.
∴OG⊥AB,∠FDO=∠GBO,OA=OB.
∴∠GAO=∠GBO.
又∠DOF=∠BOG,∴△DOF≌△BOG(ASA).
∴OG=OF.∴OG=OE.
由(1),知AA′⊥BD.又OG⊥AB,∴∠EAO=∠GAO.
∵∠EAB+∠GBO=90°,∴∠EAO+∠GAO+∠GBO=90°.
∴3∠EAO=90°.
∴∠EAO=30°.
由(1),知AA′⊥CA′.
∴tan ∠EAO==.
∴AA′=CA′.
②解:如答图2,设⊙O切CA′于点H,连接OH.
∴OH⊥CA′.
由(1),知AA′⊥CA′.∴OH∥AA′.
又AA′⊥BD,∴OE∥CA′.
∴△COH∽△CAA′,△AOE∽△ACA′.
∴==,==.
∴AA′=2OH,CA′=2OE.
∵OE=OH,∴AA′=CA′.
∴∠A′AC=∠A′CA=45°.
∴∠AOE=∠A′CA=45°.
∴AE=OE.
设AE=OE=x,则OD=OA==x.
∴DE=OD-OE=(-1)x.
在Rt△ADE中,由勾股定理,得x2 =1.
∴x2=,即OE2=.
∴S⊙O=π·OE2=π.
如图,在 ABCD中,AB=AC,作△ABC的外接圆⊙O,CD与⊙O交于点E,连接AE.
(1)求证:DA是⊙O的切线;
(1)证明:如图,连接OB,OC,连接AO并延长交BC于点M.
∵AB=AC,OB=OC,∴AM是BC的垂直平分线.
∴∠AMB=90°.
∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠DAM=∠AMB=90°.
∵OA是⊙O的半径,∴DA是⊙O的切线.
(2)若⊙O的半径为5,cos ∠BAC=,求DE的长.
(2)解:如图,∵AB=AC,AM⊥BC,∴∠BAC=2∠1.
∵∠2=2∠1,∴∠2=∠BAC.
∴cos ∠2=cos ∠BAC=.
在Rt△BOM中,OB=5,∴OM=OB·cos ∠BOM=5×=3.
∴BM===4.
∴AM=AO+OM=8,BC=2BM=8.
在Rt△ABM中,AB===4.
∴AB=AC=4.
∵四边形ABCD是平行四边形,∴AD=BC=8,∠ABC=∠D.
∵四边形ABCE是⊙O的内接四边形,∴∠ABC+∠AEC=180°.
∵∠AEC+∠AED=180°,∴∠AED=∠ABC=∠D.
∴△DAE∽△CAB,AE=AD=8.
∴=.∴=.∴DE=.
(2022·宜昌改编)已知,在△ABC中,∠ACB=90°,BC=6,以BC为直径的⊙O交AB于点H,将△ABC沿射线AC平移得到△DEF,连接BE.如图,DE与⊙O相切于点G.
(1)求证:BE=GE;
(1)证明:∵将△ABC沿射线AC平移得到△DEF,∴BE∥CF.
∵∠ACB=90°,∴∠CBE=∠ACB=90°.
∵OB是⊙O的半径,∴BE是⊙O的切线.
∵DE是⊙O的切线,∴BE=GE.
(2)求BE·CD的值.
(2)解:如图,过点D作DM⊥BE于点M.∴∠DMB=90°.
由(1),知∠CBE=∠BCF=90°.
∴四边形BCDM是矩形.∴CD=BM,DM=BC=6.
由(1),知BE=GE.同理可证CD=DG.设BE=x,CD=y.
在Rt△DME中,DM2+EM2=DE2,
∴62+(x-y)2=(x+y)2.∴xy=9,即BE·CD=9.
如图,在矩形ABCD中,AB=4,AD=3,点O是边AB上一个动点(不与点A重合),连接OD,将△OAD沿OD折叠,得到△OED;再以点O为圆心,OA的长为半径作半圆,交射线AB于点G,连接AE并延长交射线BC于点F,连接EG,设OA=x.
(1)证明:∵四边形ABCD是矩形,
∴∠DAO=90°.
∵将△OAD沿OD折叠,得到△OED,
∴∠OED=∠DAO=90°.∴OE⊥DE.
∵OE是半径,∴DE是半圆O的切线.
(1)求证:DE是半圆O的切线;
(2)当点E落在BD上时,求x的值;
(2)解:如图1,点E落在BD上.
在Rt△ADB中,∠DAB=90°,AD=3,AB=4,
∴BD===5.
∵S△ADB=S△ADO+S△BDO,
∴×3×4=×3·x+×5·x.
∴x=.
(3)当点E落在BD下方时,设△AEG与△ABF面积的比值为y,确定y与x之间的函数关系式.
(3)解:如图2,点E落在BD下方.
在Rt△DAO中,OD===.
∵DA=DE,OA=OE,∴OD垂直平分线段AE.
∵S△ADO=AD·OA=OD·AJ,
∴AJ==.
∴AE=2AJ=.
∵AG是直径,∴∠AEG=90°=∠ABF.
∵∠EAG=∠BAF,∴△AEG∽△ABF.
∴y== ==(0<x<).
第二部分 专题复习
专题八 圆的综合
01
基础回顾
02
例题精讲
目录
目录
1.如图,在△ABC中,以BC为直径作⊙O分别交AB,AC于D,E两点,AD=3,BD=5,AE=4,则EC= 2 .
2
2.(2023·聊城二模)如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=12,BC=5.则sin ∠ABD=( C )
A.
B.
C.
D.
C
如图,AB为⊙O的直径,点D,E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠A.
(1)求证:△ACD∽△DCB;
(1)证明:∵∠C=∠C,∠A=∠BDC,
∴△ACD∽△DCB.
(2)求证:CD是⊙O的切线;
(2)证明:如图,连接OD.
∵AB为⊙O的直径,∴∠ADB=90°.∴∠A+∠ABD=90°.
∵OB=OD,∴∠ABD=∠ODB.
∵∠BDC=∠A,∴∠BDC+∠ODB=90°.
∴∠ODC=90°.∴OD⊥CD.
∵OD是⊙O的半径,∴CD是⊙O的切线.
(3)若tan E=,AC=10,求⊙O的半径.
(3)解:∵∠ADB=90°,tan E=,∠E=∠A,∴tan A==.
由(1),得△DCB∽△ACD.∴===.
∵AC=10,∴=. ∴CD=6.
∴=. ∴BC=. ∴AB=AC-BC=10-=.
∴⊙O的半径为.
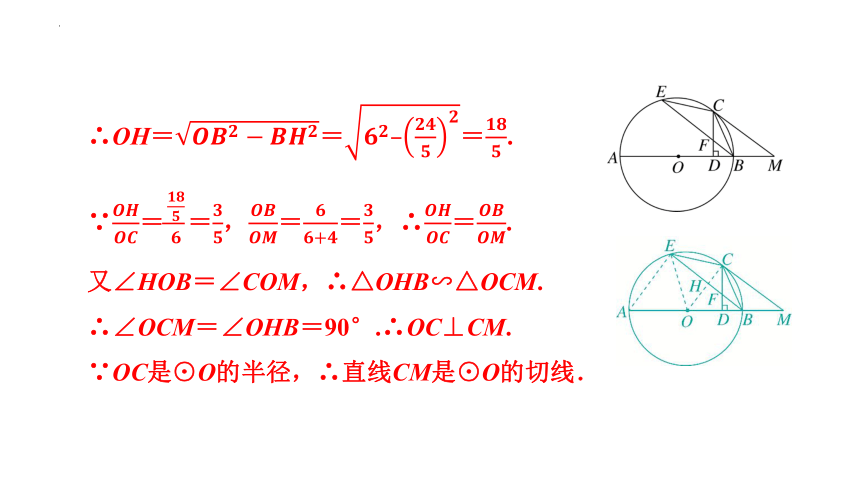
(2023·包头二模)如图,线段AB为⊙O的直径,点C,E在⊙O上,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F,CF=BF,∠BEC=∠DCB.
(1)求证:=;
证明:(1)∵CF=BF,∴∠FCB=∠FBC.
∵∠BEC=∠DCB,∴∠BEC=∠FBC.
∴BC=CE.
∴=.
(2)若cos ∠ABE=,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.(用两种证法解答)
(2)法1:如图,连接OC交BE于点H,连接OE.
∵=,∴∠BOC=∠COE.
∵BO=EO,∴OC⊥BE. ∴∠OHB=90°.
在Rt△OBH中,cos ∠OBH==,
∵OB=6,∴BH=×6=.
∴OH===.
∵==,==,∴=.
又∠HOB=∠COM,∴△OHB∽△OCM.
∴∠OCM=∠OHB=90°.∴OC⊥CM.
∵OC是⊙O的半径,∴直线CM是⊙O的切线.
法2:如图,连接AE.
∵AB为⊙O的直径,∴∠AEB=90°.
在Rt△ABE中,cos ∠ABE==,∴cos ∠BAE==.
由(1),得BC=CE.
∴∠COM=∠EOC. ∴∠EAB=∠EOB=∠COM.
∵==,∴=.
∴=. ∴△ABE∽△OMC.
∴∠AEB=∠OCM=90°. ∴OC⊥CM.
∵OC是⊙O的半径,∴直线CM是⊙O的切线.
(2023·温州三模)如图,在△ABC中,AB=AC,⊙O为△ABC的外接圆,弦BD⊥OC于点F,交AC于点E,连接CD.
(1)求证:BE=BC;
(1)证明:∵BD⊥OC,∴=.
∴∠CBE=∠CAB.
又∠ECB=∠BCA,∴△BEC∽△ABC.
∴=.
∵AB=AC,∴BE=BC.
(2)若tan ∠BCA=3,EF=2,求AB的长.
(2)解:由(1),得BE=BC.∴∠BCE=∠BEC.
∵BD⊥OC,tan ∠BCA=3,EF=2,
∴tan ∠BEC===3. ∴CF=6.
∴EC==2.
设BC=BE=x.
∵BC2=BF2+CF2,BF=BE-EF=x-2,
∴x2=(x-2)2+62. 解得x=10. ∴BC=10.
由(1),知△BEC∽△ABC.
∴=,即=. ∴AB=5.
(桂林中考)如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G,交AC于点H.
(1)求证:CD是⊙O的切线;
(1)证明:如图,连接OC.
∵OA=OC,∴∠CAO=∠ACO.
∵AC平分∠DAB,∴∠DAC=∠OAC.
∴∠DAC=∠ACO.∴AD∥OC.
∵CD⊥AD,∴OC⊥CD.
∵OC是⊙O的半径,∴CD是⊙O的切线.
(2)延长AB和DC交于点E,若AE=4BE,求cos ∠DAB的值;
(2)解:∵AE=4BE,OA=OB,设BE=x,则AB=3x.
∴OC=OB=1.5x.∴OE=2.5x.
∵AD∥OC,∴∠COE=∠DAB.
∴cos ∠DAB=cos ∠COE===.
(3)在(2)的条件下,求的值.
(3)解:由(2),知OE=2.5x,OC=1.5x.
∴EC===2x.
∵FG⊥AB,∴∠AGF=90°.
∴∠AFH+∠FAG=90°.
∵∠COE+∠E=90°,∠COE=∠DAB,
∴∠AFH=∠E.
∵∠FAH=∠EAC,∴△AHF∽△ACE.
∴=,即===.
(2023·广东)综合探究
如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A′,连接AA′交BD于点E,连接CA′.
(1)求证:AA′⊥CA′.
(1)证明:∵点A关于BD的对称点为点A′,∴AE=A′E,AA′⊥BD.
∵四边形ABCD是矩形,
∴OA=OC.∴OE∥A′C.
又AA′⊥BD,∴AA′⊥CA′.
(2)以点O为圆心,OE长为半径作圆.
①如图2,⊙O与CD相切,求证:AA′=CA′;
②如图3,⊙O与CA′相切,AD=1,求⊙O的面积.
(2)①证明:如答图1,设⊙O与CD切于点F,连接OF,并延长FO交AB于点G.
∴OF⊥CD,OF=OE.
∵四边形ABCD是矩形,
∴OD=OB=BD,AB∥CD,AC=BD,OA=AC.
∴OG⊥AB,∠FDO=∠GBO,OA=OB.
∴∠GAO=∠GBO.
又∠DOF=∠BOG,∴△DOF≌△BOG(ASA).
∴OG=OF.∴OG=OE.
由(1),知AA′⊥BD.又OG⊥AB,∴∠EAO=∠GAO.
∵∠EAB+∠GBO=90°,∴∠EAO+∠GAO+∠GBO=90°.
∴3∠EAO=90°.
∴∠EAO=30°.
由(1),知AA′⊥CA′.
∴tan ∠EAO==.
∴AA′=CA′.
②解:如答图2,设⊙O切CA′于点H,连接OH.
∴OH⊥CA′.
由(1),知AA′⊥CA′.∴OH∥AA′.
又AA′⊥BD,∴OE∥CA′.
∴△COH∽△CAA′,△AOE∽△ACA′.
∴==,==.
∴AA′=2OH,CA′=2OE.
∵OE=OH,∴AA′=CA′.
∴∠A′AC=∠A′CA=45°.
∴∠AOE=∠A′CA=45°.
∴AE=OE.
设AE=OE=x,则OD=OA==x.
∴DE=OD-OE=(-1)x.
在Rt△ADE中,由勾股定理,得x2 =1.
∴x2=,即OE2=.
∴S⊙O=π·OE2=π.
如图,在 ABCD中,AB=AC,作△ABC的外接圆⊙O,CD与⊙O交于点E,连接AE.
(1)求证:DA是⊙O的切线;
(1)证明:如图,连接OB,OC,连接AO并延长交BC于点M.
∵AB=AC,OB=OC,∴AM是BC的垂直平分线.
∴∠AMB=90°.
∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠DAM=∠AMB=90°.
∵OA是⊙O的半径,∴DA是⊙O的切线.
(2)若⊙O的半径为5,cos ∠BAC=,求DE的长.
(2)解:如图,∵AB=AC,AM⊥BC,∴∠BAC=2∠1.
∵∠2=2∠1,∴∠2=∠BAC.
∴cos ∠2=cos ∠BAC=.
在Rt△BOM中,OB=5,∴OM=OB·cos ∠BOM=5×=3.
∴BM===4.
∴AM=AO+OM=8,BC=2BM=8.
在Rt△ABM中,AB===4.
∴AB=AC=4.
∵四边形ABCD是平行四边形,∴AD=BC=8,∠ABC=∠D.
∵四边形ABCE是⊙O的内接四边形,∴∠ABC+∠AEC=180°.
∵∠AEC+∠AED=180°,∴∠AED=∠ABC=∠D.
∴△DAE∽△CAB,AE=AD=8.
∴=.∴=.∴DE=.
(2022·宜昌改编)已知,在△ABC中,∠ACB=90°,BC=6,以BC为直径的⊙O交AB于点H,将△ABC沿射线AC平移得到△DEF,连接BE.如图,DE与⊙O相切于点G.
(1)求证:BE=GE;
(1)证明:∵将△ABC沿射线AC平移得到△DEF,∴BE∥CF.
∵∠ACB=90°,∴∠CBE=∠ACB=90°.
∵OB是⊙O的半径,∴BE是⊙O的切线.
∵DE是⊙O的切线,∴BE=GE.
(2)求BE·CD的值.
(2)解:如图,过点D作DM⊥BE于点M.∴∠DMB=90°.
由(1),知∠CBE=∠BCF=90°.
∴四边形BCDM是矩形.∴CD=BM,DM=BC=6.
由(1),知BE=GE.同理可证CD=DG.设BE=x,CD=y.
在Rt△DME中,DM2+EM2=DE2,
∴62+(x-y)2=(x+y)2.∴xy=9,即BE·CD=9.
如图,在矩形ABCD中,AB=4,AD=3,点O是边AB上一个动点(不与点A重合),连接OD,将△OAD沿OD折叠,得到△OED;再以点O为圆心,OA的长为半径作半圆,交射线AB于点G,连接AE并延长交射线BC于点F,连接EG,设OA=x.
(1)证明:∵四边形ABCD是矩形,
∴∠DAO=90°.
∵将△OAD沿OD折叠,得到△OED,
∴∠OED=∠DAO=90°.∴OE⊥DE.
∵OE是半径,∴DE是半圆O的切线.
(1)求证:DE是半圆O的切线;
(2)当点E落在BD上时,求x的值;
(2)解:如图1,点E落在BD上.
在Rt△ADB中,∠DAB=90°,AD=3,AB=4,
∴BD===5.
∵S△ADB=S△ADO+S△BDO,
∴×3×4=×3·x+×5·x.
∴x=.
(3)当点E落在BD下方时,设△AEG与△ABF面积的比值为y,确定y与x之间的函数关系式.
(3)解:如图2,点E落在BD下方.
在Rt△DAO中,OD===.
∵DA=DE,OA=OE,∴OD垂直平分线段AE.
∵S△ADO=AD·OA=OD·AJ,
∴AJ==.
∴AE=2AJ=.
∵AG是直径,∴∠AEG=90°=∠ABF.
∵∠EAG=∠BAF,∴△AEG∽△ABF.
∴y== ==(0<x<).
同课章节目录
