圆锥曲线章节复习及练习题
图片预览




文档简介
高二数学圆锥曲线章节复习
一. 本周教学内容:
圆锥曲线章节复习
二. 本周教学重、难点:
1. 重点:
椭圆、双曲线、抛物线的定义、标准方程、几何性质
2. 难点:
直线和圆锥曲线的位置关系、最值问题、几何性质的应用
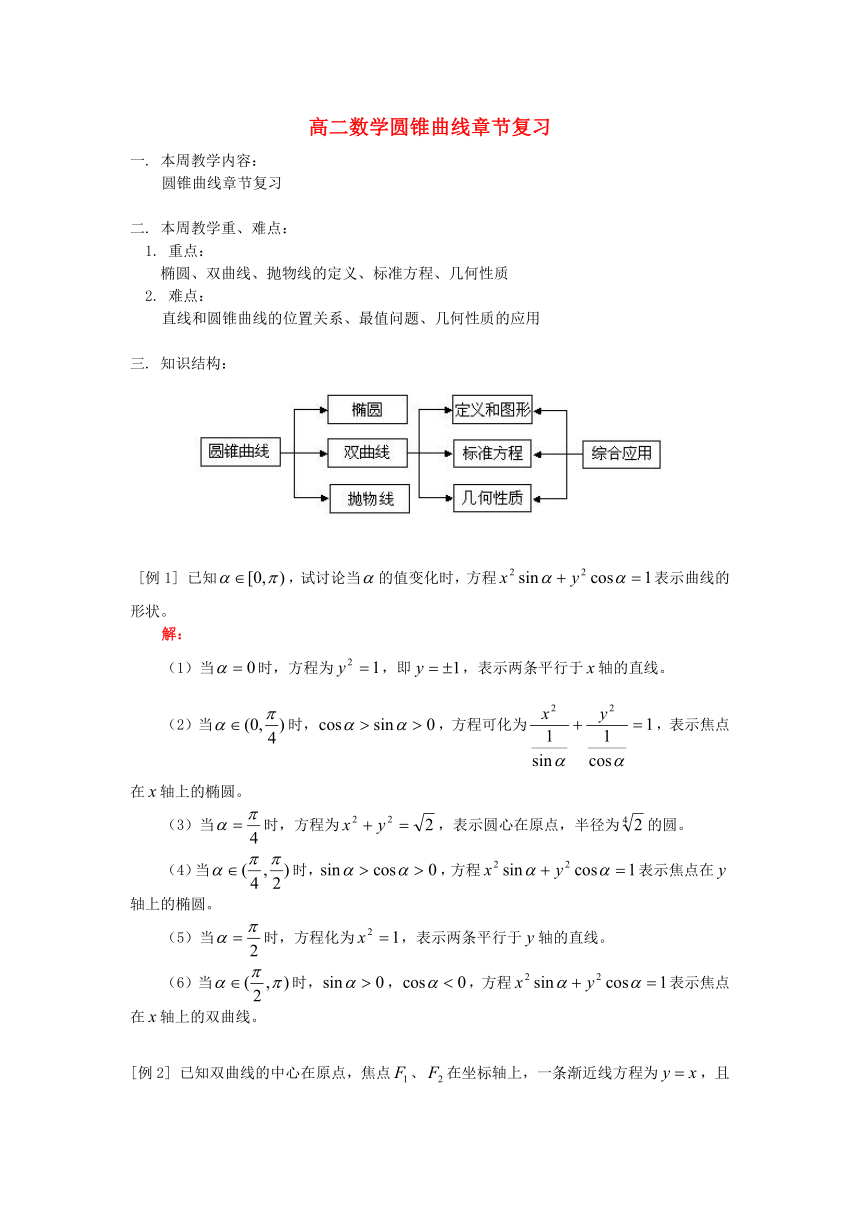
三. 知识结构:
[例1] 已知,试讨论当的值变化时,方程表示曲线的形状。
解:
(1)当时,方程为,即,表示两条平行于轴的直线。
(2)当时,,方程可化为,表示焦点在轴上的椭圆。
(3)当时,方程为,表示圆心在原点,半径为的圆。
(4)当时,,方程表示焦点在轴上的椭圆。
(5)当时,方程化为,表示两条平行于轴的直线。
(6)当时,,,方程表示焦点在轴上的双曲线。
[例2] 已知双曲线的中心在原点,焦点、在坐标轴上,一条渐近线方程为,且过点(4,)。
(1)求双曲线方程;
(2)若点M(3,)在此双曲线上,求;
(3)求的面积。
解:
(1)由题意知,双曲线的方程是标准方程
∵ 双曲线的一条渐近线方程为 ∴ 设双曲线方程为
把点(4,)代入双曲线方程得,
∴ 所求双曲线方程为
(2)由(1)知双曲线方程为
∴ 双曲线的焦点为、 ∵ M点在双曲线上
∴ ,
∴
(3)∵ ∴ ∴ 为直角三角形
∵
∴
[例3] 已知抛物线的焦点为A,以B()为圆心,长为半径,在轴上方的半圆交抛物线于不同的两点M、N,P是MN的中点。
(1)求的值;
(2)是否存在这样的值,使、、成等差数列?
解:如下图,A() ∵ ∴ 圆的方程为
与联立得
∴ 解得
设 则,
∴
(2)设P(),则,
∴
∴
∴
若、成等差数列,则
∴
解得,这与矛盾
故不存在,使成等差数列
[例4] 已知双曲线与点P(1,2),过P点作直线与双曲线交于A、B两点,若P为AB的中点。
(1)求直线AB的方程;
(2)若Q(1,1),证明:不存在以Q为中点的弦。
方法一:(1)解:设过P(1,2)点的直线为,代入双曲线方程
得
由线段AB中点为P(1,2) ∴
解得,又时,使 从而直线AB方程为
(2)证明:按同样方法求得,而使,所以直线CD不存在
方法二:设A()、B(), ①, ②
①-②得:
∴
写出直线方程,即,检验与双曲线有交点
[例5] 已知双曲线(,)的左、右两个焦点分别为F1、F2,P是它左支上一点,P到左准线的距离为,双曲线的一条渐近线为,问是否存在点P,使、、成等比数列?若存在,求出P的坐标;若不存在,请说明理由。
解:假设存在点P()满足题中条件
∵ 双曲线的一条渐近线为 ∴ ,
∴ , 即
由,得 ①
∵ 双曲线的两准线方程为 ∴
∵ 点P在双曲线的左支上
∴ 代入①得
∴ ,代入,得②
∴ 存在点P使成等比数列,点P的坐标是()
[例6] 如图,直线和相交于点M,,点N,以A、B为端点的曲线段C上的任一点到的距离与到点N的距离相等。若为锐角三角形,,=3,且,建立适当的坐标系,求曲线段C的方程。
解:方法一:以为轴,MN的中点O为原点建立如图的直角坐标系。由题意可知,曲线段C所在的抛物线在直角坐标系中的位置是标准的,并且点N是该抛物线的焦点,是准线。所以可令抛物线的方程为,过点A作,,垂足分别为Q和E,由于是锐角三角形,则点E必在线段MN上。
所以, ∵ ∴
∴
∴ 抛物线方程为
由上述可知,,点B到准线的距离为6,则点B的横坐标为4,又曲线段在轴上方,故曲线段C的方程为
方法二:以为轴,为轴建立如下图的直角坐标系,其中M点为原点,这时焦点N在轴上,顶点应是线段MN的中点。令曲线段C所在的抛物线方程为:
设
则:
由(1)-(2)得 代入(1)得
∴ ∵ ∴ ∵ ∴
代入(3)得 ∴ 曲线段C的方程为
[例7] 设分别为椭圆C:()的左、右两个焦点。
(1)若椭圆C上的点A(1,)到两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点。求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为时,那么与之积是与点P位置无关的定值。试对双曲线写出具有类似特性的性质,并加以证明。
解:(1)椭圆C的焦点在轴上 ∵ 椭圆上的点A到两点的距离和是4,得,即
又 ∵ 点A()在椭圆上 ∴ ,得
∴ ∴ 椭圆C的方程为,焦点为、
(2)设椭圆C上的动点为K(),线段F1 K的中点Q()满足:
∴
因此 即为所求的轨迹方程
(3)类似的性质为:若M、N是双曲线上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为、时,那么与之积是与点P位置无关的定值。证明如下:设点M的坐标为(),则点N的坐标为(),其中。又设点P的坐标为(),由,=,得
将,,代入得,命题得证。
[例8] 直线:与双曲线C:的右支交于不同的两点A、B。
(1)求实数的取值范围;
(2)是否存在实数,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出的值;若不存在,说明理由。
解:
(1)将直线的方程代入双曲线C的方程后,整理,得①,依题意,直线与双曲线C的右支交于不同两点,故
解得的取值范围为
(2)设A、B两点的坐标分别为,则由①式得②,假设存在实数,使得以线段AB为直径的圆经过双曲线C的右焦点F(),则由FA⊥FB得
即
整理得 ③
把②式及代入③式化简得
解得或(舍去)
可得使得以线段AB为直径的圆经过双曲线C的右焦点。
【模拟试题】(答题时间:60分钟)
一. 选择题
1. 椭圆的一条准线为,则椭圆的离心率等于( )
A. B. C. D.
2. 双曲线的离心率,则的取值范围是( B )
A. B. C. D.
3. 若椭圆(m>n>0)和双曲线有相同的左、右焦点、,P是两条曲线的一个交点,则的值是( A )
A. B. C. D.
4. 双曲线的焦点为、,弦AB过且两端点在双曲线的一支上,若,则( c )
A. 为定值 B. 为定值 C. 为定值 D. 不为定值
5. 设P是椭圆上一点,、是椭圆的两个焦点,则的最小值是( B )
A. B. C. D.
6. 若点P在抛物线上,点Q在圆上,则的最小值为( D )
A. B. C. D.
7. 抛物线上到顶点与焦点距离相等的点的坐标为( C )
A. B. C. D.
8. 将离心率为的椭圆,绕着它的左焦点按顺时针方向旋转后,所得新椭圆的一条准线方程为,则新椭圆的另一条准线方程为( )
A. B. C. D.
二. 填空题
1. 已知、是双曲线的两个焦点,PQ是经过且垂直于轴的双曲线的弦,如果,则双曲线的离心率是 。
2. 已知点是椭圆上的一点,P是椭圆上的动点,当弦AP的长度最大时,则点P的坐标是 。
3. 正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线上,这个正三角形的边长是 。
4. 抛物线的弦AB垂直于轴,若,则焦点到AB的距离为 。
三. 解答题
1. 已知中心在原点,一焦点为的椭圆被直线截得的弦的中点的横坐标为,求椭圆的方程。
2. 设AB是抛物线上的动弦,且(为常数),求弦AB中点M到轴的最近距离,并研究的情况。
3. 求抛物线上的点到直线的距离的最小值,并求取得最小值时的抛物线上的点的坐标。
一. 本周教学内容:
圆锥曲线章节复习
二. 本周教学重、难点:
1. 重点:
椭圆、双曲线、抛物线的定义、标准方程、几何性质
2. 难点:
直线和圆锥曲线的位置关系、最值问题、几何性质的应用
三. 知识结构:
[例1] 已知,试讨论当的值变化时,方程表示曲线的形状。
解:
(1)当时,方程为,即,表示两条平行于轴的直线。
(2)当时,,方程可化为,表示焦点在轴上的椭圆。
(3)当时,方程为,表示圆心在原点,半径为的圆。
(4)当时,,方程表示焦点在轴上的椭圆。
(5)当时,方程化为,表示两条平行于轴的直线。
(6)当时,,,方程表示焦点在轴上的双曲线。
[例2] 已知双曲线的中心在原点,焦点、在坐标轴上,一条渐近线方程为,且过点(4,)。
(1)求双曲线方程;
(2)若点M(3,)在此双曲线上,求;
(3)求的面积。
解:
(1)由题意知,双曲线的方程是标准方程
∵ 双曲线的一条渐近线方程为 ∴ 设双曲线方程为
把点(4,)代入双曲线方程得,
∴ 所求双曲线方程为
(2)由(1)知双曲线方程为
∴ 双曲线的焦点为、 ∵ M点在双曲线上
∴ ,
∴
(3)∵ ∴ ∴ 为直角三角形
∵
∴
[例3] 已知抛物线的焦点为A,以B()为圆心,长为半径,在轴上方的半圆交抛物线于不同的两点M、N,P是MN的中点。
(1)求的值;
(2)是否存在这样的值,使、、成等差数列?
解:如下图,A() ∵ ∴ 圆的方程为
与联立得
∴ 解得
设 则,
∴
(2)设P(),则,
∴
∴
∴
若、成等差数列,则
∴
解得,这与矛盾
故不存在,使成等差数列
[例4] 已知双曲线与点P(1,2),过P点作直线与双曲线交于A、B两点,若P为AB的中点。
(1)求直线AB的方程;
(2)若Q(1,1),证明:不存在以Q为中点的弦。
方法一:(1)解:设过P(1,2)点的直线为,代入双曲线方程
得
由线段AB中点为P(1,2) ∴
解得,又时,使 从而直线AB方程为
(2)证明:按同样方法求得,而使,所以直线CD不存在
方法二:设A()、B(), ①, ②
①-②得:
∴
写出直线方程,即,检验与双曲线有交点
[例5] 已知双曲线(,)的左、右两个焦点分别为F1、F2,P是它左支上一点,P到左准线的距离为,双曲线的一条渐近线为,问是否存在点P,使、、成等比数列?若存在,求出P的坐标;若不存在,请说明理由。
解:假设存在点P()满足题中条件
∵ 双曲线的一条渐近线为 ∴ ,
∴ , 即
由,得 ①
∵ 双曲线的两准线方程为 ∴
∵ 点P在双曲线的左支上
∴ 代入①得
∴ ,代入,得②
∴ 存在点P使成等比数列,点P的坐标是()
[例6] 如图,直线和相交于点M,,点N,以A、B为端点的曲线段C上的任一点到的距离与到点N的距离相等。若为锐角三角形,,=3,且,建立适当的坐标系,求曲线段C的方程。
解:方法一:以为轴,MN的中点O为原点建立如图的直角坐标系。由题意可知,曲线段C所在的抛物线在直角坐标系中的位置是标准的,并且点N是该抛物线的焦点,是准线。所以可令抛物线的方程为,过点A作,,垂足分别为Q和E,由于是锐角三角形,则点E必在线段MN上。
所以, ∵ ∴
∴
∴ 抛物线方程为
由上述可知,,点B到准线的距离为6,则点B的横坐标为4,又曲线段在轴上方,故曲线段C的方程为
方法二:以为轴,为轴建立如下图的直角坐标系,其中M点为原点,这时焦点N在轴上,顶点应是线段MN的中点。令曲线段C所在的抛物线方程为:
设
则:
由(1)-(2)得 代入(1)得
∴ ∵ ∴ ∵ ∴
代入(3)得 ∴ 曲线段C的方程为
[例7] 设分别为椭圆C:()的左、右两个焦点。
(1)若椭圆C上的点A(1,)到两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点。求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为时,那么与之积是与点P位置无关的定值。试对双曲线写出具有类似特性的性质,并加以证明。
解:(1)椭圆C的焦点在轴上 ∵ 椭圆上的点A到两点的距离和是4,得,即
又 ∵ 点A()在椭圆上 ∴ ,得
∴ ∴ 椭圆C的方程为,焦点为、
(2)设椭圆C上的动点为K(),线段F1 K的中点Q()满足:
∴
因此 即为所求的轨迹方程
(3)类似的性质为:若M、N是双曲线上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为、时,那么与之积是与点P位置无关的定值。证明如下:设点M的坐标为(),则点N的坐标为(),其中。又设点P的坐标为(),由,=,得
将,,代入得,命题得证。
[例8] 直线:与双曲线C:的右支交于不同的两点A、B。
(1)求实数的取值范围;
(2)是否存在实数,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出的值;若不存在,说明理由。
解:
(1)将直线的方程代入双曲线C的方程后,整理,得①,依题意,直线与双曲线C的右支交于不同两点,故
解得的取值范围为
(2)设A、B两点的坐标分别为,则由①式得②,假设存在实数,使得以线段AB为直径的圆经过双曲线C的右焦点F(),则由FA⊥FB得
即
整理得 ③
把②式及代入③式化简得
解得或(舍去)
可得使得以线段AB为直径的圆经过双曲线C的右焦点。
【模拟试题】(答题时间:60分钟)
一. 选择题
1. 椭圆的一条准线为,则椭圆的离心率等于( )
A. B. C. D.
2. 双曲线的离心率,则的取值范围是( B )
A. B. C. D.
3. 若椭圆(m>n>0)和双曲线有相同的左、右焦点、,P是两条曲线的一个交点,则的值是( A )
A. B. C. D.
4. 双曲线的焦点为、,弦AB过且两端点在双曲线的一支上,若,则( c )
A. 为定值 B. 为定值 C. 为定值 D. 不为定值
5. 设P是椭圆上一点,、是椭圆的两个焦点,则的最小值是( B )
A. B. C. D.
6. 若点P在抛物线上,点Q在圆上,则的最小值为( D )
A. B. C. D.
7. 抛物线上到顶点与焦点距离相等的点的坐标为( C )
A. B. C. D.
8. 将离心率为的椭圆,绕着它的左焦点按顺时针方向旋转后,所得新椭圆的一条准线方程为,则新椭圆的另一条准线方程为( )
A. B. C. D.
二. 填空题
1. 已知、是双曲线的两个焦点,PQ是经过且垂直于轴的双曲线的弦,如果,则双曲线的离心率是 。
2. 已知点是椭圆上的一点,P是椭圆上的动点,当弦AP的长度最大时,则点P的坐标是 。
3. 正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线上,这个正三角形的边长是 。
4. 抛物线的弦AB垂直于轴,若,则焦点到AB的距离为 。
三. 解答题
1. 已知中心在原点,一焦点为的椭圆被直线截得的弦的中点的横坐标为,求椭圆的方程。
2. 设AB是抛物线上的动弦,且(为常数),求弦AB中点M到轴的最近距离,并研究的情况。
3. 求抛物线上的点到直线的距离的最小值,并求取得最小值时的抛物线上的点的坐标。
