2023-2024杭州市西湖区数学九年级上学期期末模拟卷(含答案)
文档属性
| 名称 | 2023-2024杭州市西湖区数学九年级上学期期末模拟卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 16:50:18 | ||
图片预览



文档简介
2023-2024杭州市西湖区数学九年级上学期期末模拟卷
考试范围:九年级上册全书,九年级下册第一章
姓名: 学号: 考号: 成绩: i
考生须知:
本试卷分试题卷和答题卷两部分,满分120分,考试时间120分钟。
答题前,必须在答题卡上填写校名,班级,姓名,座位号。
3. 不允许使用计算器进行计算,凡题目中没有要求取近似值的,结果应保留根号或
一、选择题(本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若,则的值为( )
A. B.3 C.4 D.
2.在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )
A. B. C. D.
3.一个不遇明的盒子中装有10个除颜色外无其他差别的小球,其中有1个黄球和3个绿球,其余都是红球,从中随机摆出一个小球.下列判断正确的是( )
甲:摸到血球比摸到黄球的可能性大;乙:镁到红球的概率为
A.甲、乙都对 B.甲、乙都不对
C.只有甲对 D.只有乙对
4.如图,,且,,则的长为( )
A.6 B.9 C.3 D.4
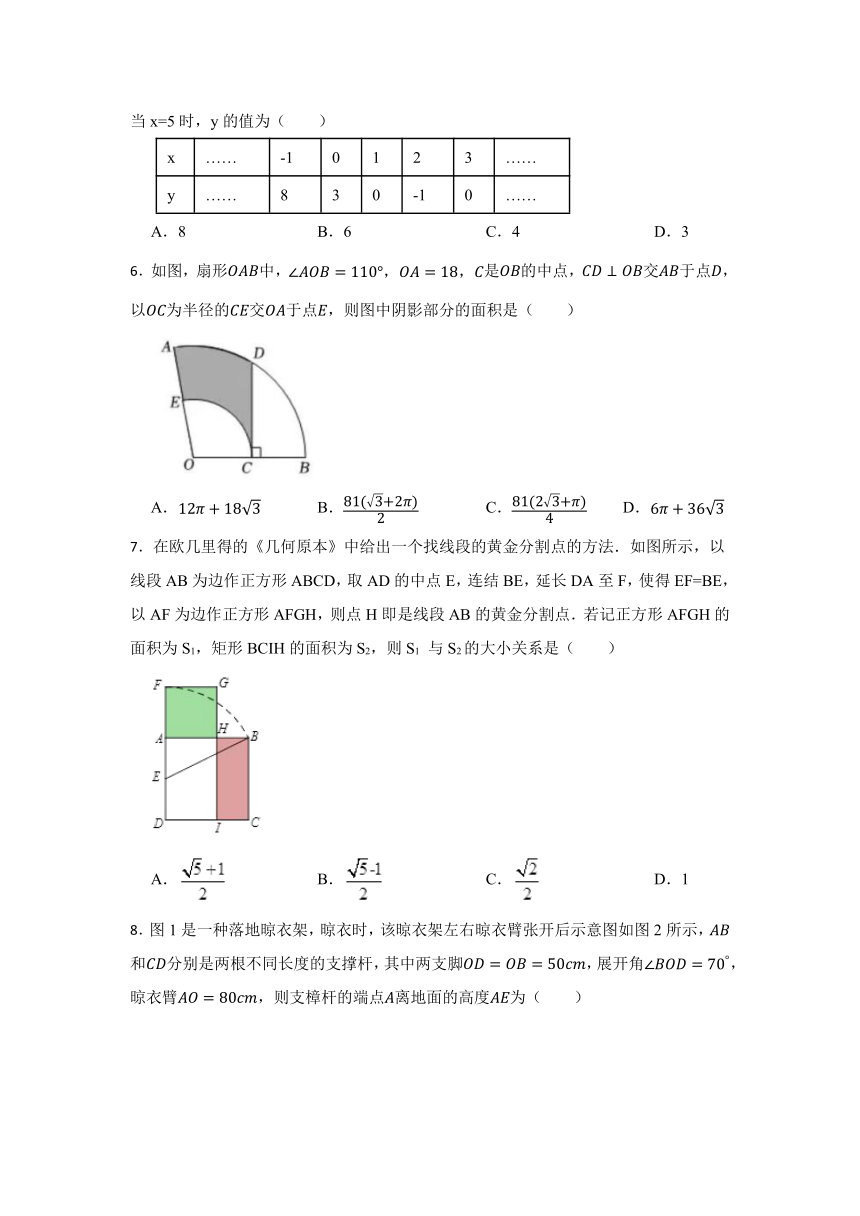
5.某同学在用列表描点法画二次函数y=ax2+bx+c的图糸时,列出了下面的表格:那么当x=5时,y的值为( )
x …… -1 0 1 2 3 ……
y …… 8 3 0 -1 0 ……
A.8 B.6 C.4 D.3
6.如图,扇形中,是的中点,交于点,以为半径的交于点,则图中阴影部分的面积是( )
A. B. C. D.
7.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1 与S2的大小关系是( )
A. B. C. D.1
8.图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚,展开角,晾衣臂,则支樟杆的端点离地面的高度为( )
A. B. C. D.
9.如图,⊙O的半径是6,AB是⊙O的弦,C是AB上一点,AC=6,BC=2,点P是⊙O上一动点,则点P与点C之间的最大距离是( )
A.6+ B.12 C.6+ D.不存在
10.如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( )
A.①③④ B.①②④ C.②③④ D.①②③④
二、填空题(本大题有6个小题,每小题4分,共24分)
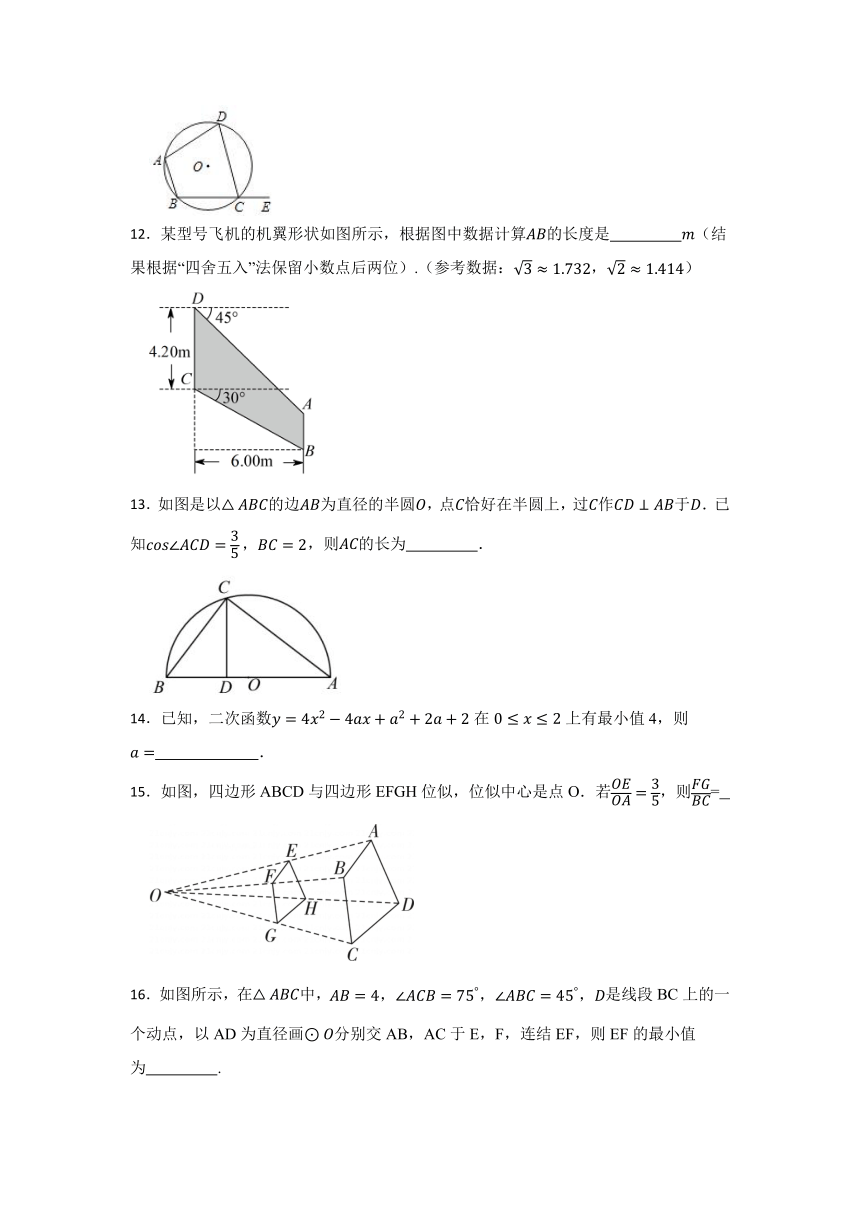
11.如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=105°,则∠DCE的度数是 °.
12.某型号飞机的机翼形状如图所示,根据图中数据计算的长度是 (结果根据“四舍五入”法保留小数点后两位).(参考数据:,)
13.如图是以的边为直径的半圆,点恰好在半圆上,过作于.已知,则的长为 .
14.已知,二次函数在上有最小值4,则 .
15.如图,四边形ABCD与四边形EFGH位似,位似中心是点O.若,则=
16.如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为 .
三、解答题(本大题有7小题,共66分,解答应写出文字说明、证明过程或演算步骤)
17.嘉嘉和淇淇周末相约到公园展练,公园有A,B两个入口,他们可以随机选择一个入口进入,假设选择每个入口的可能性相同.
(1)嘉嘉选择从A入口进入公园的概率为 ;
(2)补全如图所示的树状图,并求两人选择不同入口进入公园的概率.
18.如图,是的角平分线,在上取点E,使
(1)求证:;
(2)若,,求的度数.
19.掷实心球是某市中考体育考试的选考项目.已知一名男生投实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图所示,掷出时起点处高度为2m,当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数解析式;
(2)根据该市2023年中考体育考试评分标准(男生),投掷过程中,实心球从起点到落地点的水平距离不小于12.4m,此项考试得分为满分17分.按此评分标准,该生在此项考试中是否得满分,请说明理由.
20.动感单车是一种新型的运动器械.图1是一辆动感单车的实物图,图2是其侧面示意图.△BCD为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm,∠BCD的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度(结果精确到1cm).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
21.如图,内接于⊙O,交⊙O于点D,交于点E,交⊙O于点F,连接.
(1)求证:;
(2)若⊙O的半径为3,,求的长(结果保留π).
22.如图,已知点在二次函数的图像上,且.
(1)若二次函数的图像经过点.
①求这个二次函数的表达式;
②若,求顶点到的距离;
(2)当时,二次函数的最大值与最小值的差为1,点M,N在对称轴的异侧,求a的取值范围.
23.已知:的两条弦,相交于点M,且.
(1)如图1,连接.求证:.
(2)如图2,若,点E为弧上一点,,交于点F,连接、.
①求的度数(用含的代数式表示).
②若,,求的面积.
2023-2024杭州市西湖区数学九年级上学期期末模拟卷参考答案
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】A
10.【答案】B
11.【答案】105
12.【答案】1.66
13.【答案】
14.【答案】1或
15.【答案】
16.【答案】
17.【答案】(1)
(2)解:如图,
所有出现的等可能性结果共有4种,其中两人选择不同入口进入公园的结果有2种,
∴两人选择不同入口进入公园的概率为.
18.【答案】(1)证明:是的角平分线,
,
,
,
(2)解:,
,,
,
,
是的角平分线,
,
,
19.【答案】(1)解:根据题意设y关于x的函数表达式为:
,
把(0,2)代入解析式得,
,
解得:,
∴y关于x的函数表达式为:;
(2)解:该生在此项考试中得不到满分,理由:
当y=0,则,,
解得:x1=12,x2=﹣1(舍去),
∵12<12.4,
∴该生在此项考试中得不到满分.
20.【答案】解:在Rt△ACE中,∠AEC=90°,∠ACE=58°,AC=AB+BC=34+70=104(cm),
∵sin∠ACE=,即sin58°=,
∴AE=104×0.85=88.4≈88(cm),
∴点A到CD的距离AE的长度约为88cm.
21.【答案】(1)证明:∵,,
∴四边形为平行四边形,
∴,
∵,
∴,
∴.
(2)解:连接,如图,
由(1)得,
∵,
∴,
∴的长.
22.【答案】1)解:①将点代入中,
∴,解得,
∴二次函数的表达式为:;
②当时,此时为平行x轴的直线,
将代入二次函数中得到:,
将代入二次函数中得到:,
∵,
∴=,
整理得到:,
又∵,代入上式得到:,解出,
∴,即直线为:,
又二次函数的顶点坐标为(2,-1),
∴顶点(2,-1)到的距离为;
(2)解:若M,N在对称轴的异侧,,
∴x1+3>2,
∴x1>-1,
∵
∴,
∴-1<,
∵函数的最大值为y1=a(x1-2)2-1,最小值为-1,
∴y-(-1)=1,
∴a=,
∴,
∴;
若M、N在对称轴的异侧,,x1<2,
∵,
∴,
∵函数的最大值为y=a(x2-2)2-1,最小值为-1,
∴y-(-1)=1,
∴a=,
∴,
∴,
综上所述,a的取值范围为.
23.【答案】(1)证明:如图1,
∵,
∴=,即+=+
∴=
∴,
∴;
(2)解:①.
理由如下:
连接,如图,
∵==
∴,
∵,
∴,
∴;
②∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,解得,
∴,
∴.
考试范围:九年级上册全书,九年级下册第一章
姓名: 学号: 考号: 成绩: i
考生须知:
本试卷分试题卷和答题卷两部分,满分120分,考试时间120分钟。
答题前,必须在答题卡上填写校名,班级,姓名,座位号。
3. 不允许使用计算器进行计算,凡题目中没有要求取近似值的,结果应保留根号或
一、选择题(本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若,则的值为( )
A. B.3 C.4 D.
2.在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )
A. B. C. D.
3.一个不遇明的盒子中装有10个除颜色外无其他差别的小球,其中有1个黄球和3个绿球,其余都是红球,从中随机摆出一个小球.下列判断正确的是( )
甲:摸到血球比摸到黄球的可能性大;乙:镁到红球的概率为
A.甲、乙都对 B.甲、乙都不对
C.只有甲对 D.只有乙对
4.如图,,且,,则的长为( )
A.6 B.9 C.3 D.4
5.某同学在用列表描点法画二次函数y=ax2+bx+c的图糸时,列出了下面的表格:那么当x=5时,y的值为( )
x …… -1 0 1 2 3 ……
y …… 8 3 0 -1 0 ……
A.8 B.6 C.4 D.3
6.如图,扇形中,是的中点,交于点,以为半径的交于点,则图中阴影部分的面积是( )
A. B. C. D.
7.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1 与S2的大小关系是( )
A. B. C. D.1
8.图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚,展开角,晾衣臂,则支樟杆的端点离地面的高度为( )
A. B. C. D.
9.如图,⊙O的半径是6,AB是⊙O的弦,C是AB上一点,AC=6,BC=2,点P是⊙O上一动点,则点P与点C之间的最大距离是( )
A.6+ B.12 C.6+ D.不存在
10.如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( )
A.①③④ B.①②④ C.②③④ D.①②③④
二、填空题(本大题有6个小题,每小题4分,共24分)
11.如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD=105°,则∠DCE的度数是 °.
12.某型号飞机的机翼形状如图所示,根据图中数据计算的长度是 (结果根据“四舍五入”法保留小数点后两位).(参考数据:,)
13.如图是以的边为直径的半圆,点恰好在半圆上,过作于.已知,则的长为 .
14.已知,二次函数在上有最小值4,则 .
15.如图,四边形ABCD与四边形EFGH位似,位似中心是点O.若,则=
16.如图所示,在中,是线段BC上的一个动点,以AD为直径画分别交AB,AC于E,F,连结EF,则EF的最小值为 .
三、解答题(本大题有7小题,共66分,解答应写出文字说明、证明过程或演算步骤)
17.嘉嘉和淇淇周末相约到公园展练,公园有A,B两个入口,他们可以随机选择一个入口进入,假设选择每个入口的可能性相同.
(1)嘉嘉选择从A入口进入公园的概率为 ;
(2)补全如图所示的树状图,并求两人选择不同入口进入公园的概率.
18.如图,是的角平分线,在上取点E,使
(1)求证:;
(2)若,,求的度数.
19.掷实心球是某市中考体育考试的选考项目.已知一名男生投实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图所示,掷出时起点处高度为2m,当水平距离为时,实心球行进至最高点处.
(1)求y关于x的函数解析式;
(2)根据该市2023年中考体育考试评分标准(男生),投掷过程中,实心球从起点到落地点的水平距离不小于12.4m,此项考试得分为满分17分.按此评分标准,该生在此项考试中是否得满分,请说明理由.
20.动感单车是一种新型的运动器械.图1是一辆动感单车的实物图,图2是其侧面示意图.△BCD为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm,∠BCD的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度(结果精确到1cm).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
21.如图,内接于⊙O,交⊙O于点D,交于点E,交⊙O于点F,连接.
(1)求证:;
(2)若⊙O的半径为3,,求的长(结果保留π).
22.如图,已知点在二次函数的图像上,且.
(1)若二次函数的图像经过点.
①求这个二次函数的表达式;
②若,求顶点到的距离;
(2)当时,二次函数的最大值与最小值的差为1,点M,N在对称轴的异侧,求a的取值范围.
23.已知:的两条弦,相交于点M,且.
(1)如图1,连接.求证:.
(2)如图2,若,点E为弧上一点,,交于点F,连接、.
①求的度数(用含的代数式表示).
②若,,求的面积.
2023-2024杭州市西湖区数学九年级上学期期末模拟卷参考答案
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】A
10.【答案】B
11.【答案】105
12.【答案】1.66
13.【答案】
14.【答案】1或
15.【答案】
16.【答案】
17.【答案】(1)
(2)解:如图,
所有出现的等可能性结果共有4种,其中两人选择不同入口进入公园的结果有2种,
∴两人选择不同入口进入公园的概率为.
18.【答案】(1)证明:是的角平分线,
,
,
,
(2)解:,
,,
,
,
是的角平分线,
,
,
19.【答案】(1)解:根据题意设y关于x的函数表达式为:
,
把(0,2)代入解析式得,
,
解得:,
∴y关于x的函数表达式为:;
(2)解:该生在此项考试中得不到满分,理由:
当y=0,则,,
解得:x1=12,x2=﹣1(舍去),
∵12<12.4,
∴该生在此项考试中得不到满分.
20.【答案】解:在Rt△ACE中,∠AEC=90°,∠ACE=58°,AC=AB+BC=34+70=104(cm),
∵sin∠ACE=,即sin58°=,
∴AE=104×0.85=88.4≈88(cm),
∴点A到CD的距离AE的长度约为88cm.
21.【答案】(1)证明:∵,,
∴四边形为平行四边形,
∴,
∵,
∴,
∴.
(2)解:连接,如图,
由(1)得,
∵,
∴,
∴的长.
22.【答案】1)解:①将点代入中,
∴,解得,
∴二次函数的表达式为:;
②当时,此时为平行x轴的直线,
将代入二次函数中得到:,
将代入二次函数中得到:,
∵,
∴=,
整理得到:,
又∵,代入上式得到:,解出,
∴,即直线为:,
又二次函数的顶点坐标为(2,-1),
∴顶点(2,-1)到的距离为;
(2)解:若M,N在对称轴的异侧,,
∴x1+3>2,
∴x1>-1,
∵
∴,
∴-1<,
∵函数的最大值为y1=a(x1-2)2-1,最小值为-1,
∴y-(-1)=1,
∴a=,
∴,
∴;
若M、N在对称轴的异侧,,x1<2,
∵,
∴,
∵函数的最大值为y=a(x2-2)2-1,最小值为-1,
∴y-(-1)=1,
∴a=,
∴,
∴,
综上所述,a的取值范围为.
23.【答案】(1)证明:如图1,
∵,
∴=,即+=+
∴=
∴,
∴;
(2)解:①.
理由如下:
连接,如图,
∵==
∴,
∵,
∴,
∴;
②∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,解得,
∴,
∴.
同课章节目录
