冀教版数学六上《测量旗杆高度》课件
图片预览











文档简介
课件31张PPT。测量旗杆的高度
教学目标:
1、在测量旗杆的具体问题情境中,进一步理解相似三角形概念及其性质。
2、应用相似三角形概念及其性质解决有关实际问题,发展学生的数学应用意识。
3、积累数学操作活动经验,培养学生的问题意识,提高分析问题和解决问题的能力。 教学重点:
能灵活应用相似三角形的性质解决有关实际问题。
教学难点 :
不同条件下解决实际问题中数学操作活动的原理及其方法的选取。
教学过程:
本节内容2课时,第一节是室外测量活动课,第二节内堂课的实录. (一)导入新课---问题情景
教师:同学们,我们知道数学来源于生活,反过来又为生活生产服务。今天我们一起来交流和探讨利用相似三角形的有关知识测量旗杆高度的问题。
计算机显示课题:测量旗杆的高度
教师:我们已经让大家分组完成测量我们学校的旗杆的高度问题。哪个小组把你们的测量结果向大家汇报一下?
?(二)进入新课---尝试建立模型?
小明:让我们小组先来吧。
教师:你们是星期六完成的吗?
小明:不是。
教师:为什么?
小明:下小雨了。
教师:噢,那是什么时候完成的?
小明:星期天完成的,星期天有太阳。
(大部分小组是在星期天完成的,有些小组是在星期六完成的)
教师:能把你们组测量的数据展示给同学们吗?
小明:可以。教师:通过测量这些数据你发现了什么规律?
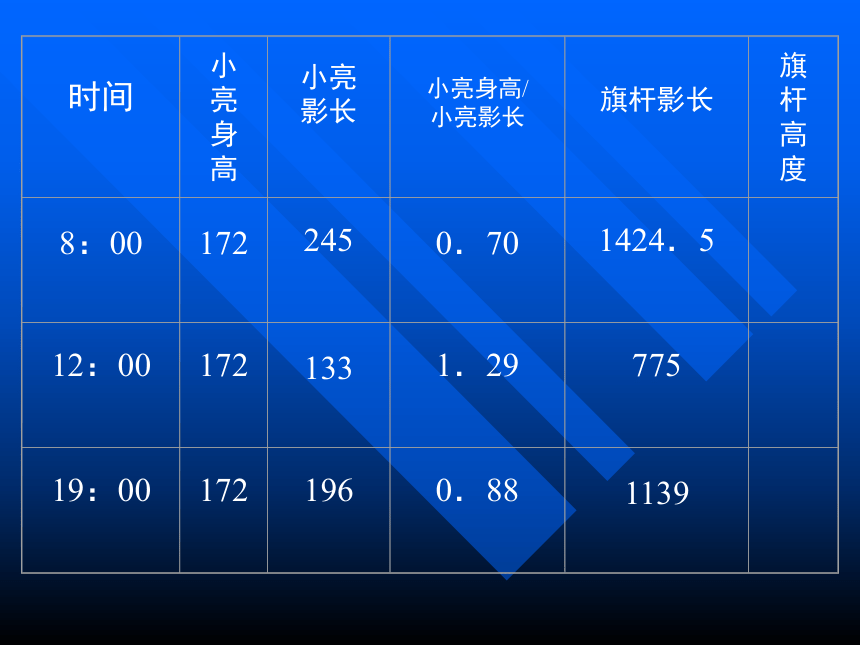
小明:早晨太阳刚升起,我的影长比身高长;正午时,我的影长比身高短;太阳快落山时,我的影长比身高又长了。
教师:还有要补充的吗?
小明小组:没有了。
教师:请坐。
教师:小兵,你们组呢?
小兵:和小明他们组一样。教师:其他同学还有什么发现吗?
学生:没有了。
学生1:小明和小亮身高虽然不一样,但在同一时刻,小明身高与影长之比与小亮的身高与影长之比相等。
教师:太棒了!这个比值与你们组的计算的结果相比呢?
学生1:一样的.
教师:很好,请坐。(板书:在同一时刻,两个物体的高度与它们的影长成比例。)
教师:根据你们测量的数据能求出旗杆的高度吗?
学生:可以。教师:全班一起计算旗杆高度,计算出结果后告诉老师。
教师:算好了请举手……“学生2”请回答。
学生2:9. 98米。
教师:请坐。有不同答案吗?
学生3:9.99米。
教师:请坐。
教师:大约是10米,还有其它答案吗?
学生:都差不多。
教师:谁来说一下,你是如何求出旗杆高度的?
学生4:在同一时刻,旗杆及影长、旗杆的顶端和影子的端点连起来可构成一个直角三角形;同样人及影子、头顶和影子的端点连起来也可构成一个直角三角形。这两个直角三角形相似,所以小明身高比小明影长等于旗杆高度比旗杆影长。把小明身高、影长及旗杆影长的数值代入即可以求出旗杆高度。
学生5:我觉得在同一时刻即早上8:00时,我用小明的身高与小明影长之比0.7去乘以旗杆的影长14.25就可以了。教师:他们说的对吗?
学生:都对。
(大屏幕显示)
教师:事实上,他们都是利用构造相似三角形的办法求出旗杆的高度的,与小明占的位置有关系吗?
学生:没有关系。
教师演示(拖动鼠标,变换△DEF的位置)。
教师:这里必须具备一个条件:晴天有阳光。
学生6:老师,如果是夜晚他们小组的这种方法还可以这样测量吗?显然不行。
学生:不行!……可以!有月光也可以。
教师:这个问题提的很好!要是在阴天,你们还能测出旗杆的高度吗?
(三)深化新内容---解释、应用和发展
?
(……四人小组可讨论一下,看有什么办法可以测出旗杆高度?)
学生8:可以用吊车把人吊上去,皮尺测量旗杆的高度。
学生7:这样做是不是成本太大了,要花很多钱的.
学生9:可以用照像机。
学生7:怎样做?
学生6:让一个人站在旗杆下照一张照片,测一下照片上旗杆是照片中的人身高的几倍,而人的身高是已知的,马上可算出旗杆高度。教师:完全可以,花钱不太多,想一想能不花钱就测量出旗杆的高呢?
学生10:先把红旗放下来,拴上一根绳子(或皮尺),然后再升上去,在绳子了上做一个记号,然后再放下来,测出绳子的长度(或读出皮尺刻度)就可以了。学生11:我补充一下,还要估计红旗升到顶部的位置与旗杆顶端还差多少。
教师:很好!请坐。还有吗?
学生12:可利用刻度尺进行目测,我们小组就是这么做的。
教师:你给大家演示一下怎样目测。
学生12:就这样……(大屏幕演示)
教师:是这样吗? 学生12:是的。
教师:需要测出哪些数据?
学生12:测出BF的长,再测出眼睛到尺子的距离就可以了。过E作EM⊥CD于M,就有EM/BF=CD/AB把EM、BF的值及CD的读数值代入就可以求旗杆高AB了。
学生13:我有些太懂,BF不在三角形里,怎么比?
学生14:BF可看作E到AB的距离,利用相似三角形对应高的比也等于对应边之比求解。
学生13:懂了。
教师:哪个小组还有还有没有其它方法?
…… 教师:你们在家站在穿衣镜前看不到脚怎么办?
学生:往后退一点。
学生15:我知道啦,可以把镜子放在地面上利用镜子的反射来求旗杆的高。
教师:能给大家讲清楚你怎么做的?
学生15:我想找一个人帮忙,比如小颖,让小颖站在离开旗杆底部大约10米左右的地方,把镜子放在她与旗杆之间,靠近小颖的地方,小颖只要通过镜子能看到旗杆顶端就可以了。 教师:(用计算机大屏幕演示)
教师:是这样吗? 学生15:是的,若看不到旗杆顶端,就让小颖向前或向后移动一下就可以了,这时只需要测出BC、CD的长,小颖的身高是1.65米,即AB/DE=BC/CD。
学生16:你怎么知道△ABC与△EDC相似呢?
学生15:利用光的入射角等于反射角。教师:很好。都请坐。这里是不是可以返回到方案(一)中,若有阳光的晴天里,把镜子放在旗杆影子的顶端,让小颖站在旗杆影子上使她的头部的影子与旗杆影子的顶部重合,这就可近似地∠DCE=∠ACE了吗?
学生16:噢,是个好办法!
教师:今天的课就上到这,有兴趣的同学写课后可以再想一想,还有没有其它的办法求旗杆的高度?(四)回顾与总结
教师:下面请同学们想一想你这节课有哪些收获?
学生17:我学会了测量旗杆高的多种方法。
学生18:学会了运用相似形的有关知识求旗杆的高。
学生19:我体会到交流的快乐。大家有不同的方法,彼此交流可以使我们互相学习。
教师:很好!
学生20:相似三角形及其性质有着广泛的应用。
学生21:要灵活的应用相似三角形的知识,应根据具体情况选用不同的方法。晴天时利用物高与影长成比例(包括使用小镜子);阴天时使用手拿刻度尺进行目测,也可以使用小镜子(入射角等于反射角原理得到比例)。
教师:当然,晴天时也可以使用手拿刻度尺进行目测的办法。大家总结的都很好,我们既要注意把现实问题抽象成数学问题,比如构造相似三角形解决一些实际问题。还应注意根据具体情况,(比如晴天与阴天)灵活地选用不同的操作方法。通过今天的学习,你们还有哪些疑惑?
学生20:有些方法我们想不到怎么办?
教师:应该仔细地观察生活,理解题意,分析问题所处的环境,多尝试不同的数学操作活动,探索解决问题的策略;只要多动脑、勤操作,相信同学们一定比我行!(学生鼓掌,教师板书:观察生活——理解题意——分析条件——操作活动)
学生22:利用相似三角形能不能测量其它物体的高?
学生23:可以的,比如树高、电线杆、楼房的高度等。
教师:金字塔是古代埃及的著名建筑,它的底部很大,它的高度是如何测量的?请同学们先阅读课本中的“读一读”内容,再想一想操作活动的办法,下一节课我们再交流。
测量旗杆(或建筑物)的高度,是相似三角形知识应用的一个典型现实问题。从本节课的教学过程,我们可以看到,教师在处理和把握上有如下的特点: 点 评 1、立足于以展示数学活动和合作交流的方式组织教学。
教师首先检查了所安排的活动“不同时刻,身高与影长的比例关系”小组合作的完成情况,从活动经验中得到“在同一时刻,两个物体的高度与它们的影长成比例”这一数学活动事实,并把它应用到求旗杆高度问题中,过渡自然,应用合理。在新课程实施时,我们必需清醒的看到:在基础知识和基本技能游刃有余的背后,隐藏着解决实际问题时数学操作经验缺乏的严重问题。在本节课的教学中,针对各种不同条件下测旗杆高度问题,教师都以组织学生开展数学活动和合作交流为基本的教法和学法。
2、注意培养学生的问题意识。
在数学课堂教学中,我们经常讲“培养学生分析问题和解决问题的能力”,但基本上由教师包办代替了,而“由学生主动的提出问题”基本上做不到。
可以看出,本节课教师在培养学生问题意识中所设计的问题串大致是:
(1)在同一时刻,两个物体的高度与影长有什么关系?
(2)旗杆的高度与人所站的位置有关系吗?为什么?
(3)还有其他测旗杆高的方法吗?为什么?
(4)在没有影子(阴天)的情况下,还能测旗杆高吗?为什么?
(5)如何才能想到多种办法,灵活地解决问题?
在教学过程中有几个闪亮点,如,学生提出了“阴天(没有影子)时,如何测旗杆高?”等问题。 3、培养自主探索、合作交流的学习方法和习惯。
教学中,教师注意发挥学生的主观能动性。在活动中及问题提出后,教师并不急于回答,问题完全由学生自主探索、合作交流去解决,教师只是适时的点拨、引导和补充完善。
教学目标:
1、在测量旗杆的具体问题情境中,进一步理解相似三角形概念及其性质。
2、应用相似三角形概念及其性质解决有关实际问题,发展学生的数学应用意识。
3、积累数学操作活动经验,培养学生的问题意识,提高分析问题和解决问题的能力。 教学重点:
能灵活应用相似三角形的性质解决有关实际问题。
教学难点 :
不同条件下解决实际问题中数学操作活动的原理及其方法的选取。
教学过程:
本节内容2课时,第一节是室外测量活动课,第二节内堂课的实录. (一)导入新课---问题情景
教师:同学们,我们知道数学来源于生活,反过来又为生活生产服务。今天我们一起来交流和探讨利用相似三角形的有关知识测量旗杆高度的问题。
计算机显示课题:测量旗杆的高度
教师:我们已经让大家分组完成测量我们学校的旗杆的高度问题。哪个小组把你们的测量结果向大家汇报一下?
?(二)进入新课---尝试建立模型?
小明:让我们小组先来吧。
教师:你们是星期六完成的吗?
小明:不是。
教师:为什么?
小明:下小雨了。
教师:噢,那是什么时候完成的?
小明:星期天完成的,星期天有太阳。
(大部分小组是在星期天完成的,有些小组是在星期六完成的)
教师:能把你们组测量的数据展示给同学们吗?
小明:可以。教师:通过测量这些数据你发现了什么规律?
小明:早晨太阳刚升起,我的影长比身高长;正午时,我的影长比身高短;太阳快落山时,我的影长比身高又长了。
教师:还有要补充的吗?
小明小组:没有了。
教师:请坐。
教师:小兵,你们组呢?
小兵:和小明他们组一样。教师:其他同学还有什么发现吗?
学生:没有了。
学生1:小明和小亮身高虽然不一样,但在同一时刻,小明身高与影长之比与小亮的身高与影长之比相等。
教师:太棒了!这个比值与你们组的计算的结果相比呢?
学生1:一样的.
教师:很好,请坐。(板书:在同一时刻,两个物体的高度与它们的影长成比例。)
教师:根据你们测量的数据能求出旗杆的高度吗?
学生:可以。教师:全班一起计算旗杆高度,计算出结果后告诉老师。
教师:算好了请举手……“学生2”请回答。
学生2:9. 98米。
教师:请坐。有不同答案吗?
学生3:9.99米。
教师:请坐。
教师:大约是10米,还有其它答案吗?
学生:都差不多。
教师:谁来说一下,你是如何求出旗杆高度的?
学生4:在同一时刻,旗杆及影长、旗杆的顶端和影子的端点连起来可构成一个直角三角形;同样人及影子、头顶和影子的端点连起来也可构成一个直角三角形。这两个直角三角形相似,所以小明身高比小明影长等于旗杆高度比旗杆影长。把小明身高、影长及旗杆影长的数值代入即可以求出旗杆高度。
学生5:我觉得在同一时刻即早上8:00时,我用小明的身高与小明影长之比0.7去乘以旗杆的影长14.25就可以了。教师:他们说的对吗?
学生:都对。
(大屏幕显示)
教师:事实上,他们都是利用构造相似三角形的办法求出旗杆的高度的,与小明占的位置有关系吗?
学生:没有关系。
教师演示(拖动鼠标,变换△DEF的位置)。
教师:这里必须具备一个条件:晴天有阳光。
学生6:老师,如果是夜晚他们小组的这种方法还可以这样测量吗?显然不行。
学生:不行!……可以!有月光也可以。
教师:这个问题提的很好!要是在阴天,你们还能测出旗杆的高度吗?
(三)深化新内容---解释、应用和发展
?
(……四人小组可讨论一下,看有什么办法可以测出旗杆高度?)
学生8:可以用吊车把人吊上去,皮尺测量旗杆的高度。
学生7:这样做是不是成本太大了,要花很多钱的.
学生9:可以用照像机。
学生7:怎样做?
学生6:让一个人站在旗杆下照一张照片,测一下照片上旗杆是照片中的人身高的几倍,而人的身高是已知的,马上可算出旗杆高度。教师:完全可以,花钱不太多,想一想能不花钱就测量出旗杆的高呢?
学生10:先把红旗放下来,拴上一根绳子(或皮尺),然后再升上去,在绳子了上做一个记号,然后再放下来,测出绳子的长度(或读出皮尺刻度)就可以了。学生11:我补充一下,还要估计红旗升到顶部的位置与旗杆顶端还差多少。
教师:很好!请坐。还有吗?
学生12:可利用刻度尺进行目测,我们小组就是这么做的。
教师:你给大家演示一下怎样目测。
学生12:就这样……(大屏幕演示)
教师:是这样吗? 学生12:是的。
教师:需要测出哪些数据?
学生12:测出BF的长,再测出眼睛到尺子的距离就可以了。过E作EM⊥CD于M,就有EM/BF=CD/AB把EM、BF的值及CD的读数值代入就可以求旗杆高AB了。
学生13:我有些太懂,BF不在三角形里,怎么比?
学生14:BF可看作E到AB的距离,利用相似三角形对应高的比也等于对应边之比求解。
学生13:懂了。
教师:哪个小组还有还有没有其它方法?
…… 教师:你们在家站在穿衣镜前看不到脚怎么办?
学生:往后退一点。
学生15:我知道啦,可以把镜子放在地面上利用镜子的反射来求旗杆的高。
教师:能给大家讲清楚你怎么做的?
学生15:我想找一个人帮忙,比如小颖,让小颖站在离开旗杆底部大约10米左右的地方,把镜子放在她与旗杆之间,靠近小颖的地方,小颖只要通过镜子能看到旗杆顶端就可以了。 教师:(用计算机大屏幕演示)
教师:是这样吗? 学生15:是的,若看不到旗杆顶端,就让小颖向前或向后移动一下就可以了,这时只需要测出BC、CD的长,小颖的身高是1.65米,即AB/DE=BC/CD。
学生16:你怎么知道△ABC与△EDC相似呢?
学生15:利用光的入射角等于反射角。教师:很好。都请坐。这里是不是可以返回到方案(一)中,若有阳光的晴天里,把镜子放在旗杆影子的顶端,让小颖站在旗杆影子上使她的头部的影子与旗杆影子的顶部重合,这就可近似地∠DCE=∠ACE了吗?
学生16:噢,是个好办法!
教师:今天的课就上到这,有兴趣的同学写课后可以再想一想,还有没有其它的办法求旗杆的高度?(四)回顾与总结
教师:下面请同学们想一想你这节课有哪些收获?
学生17:我学会了测量旗杆高的多种方法。
学生18:学会了运用相似形的有关知识求旗杆的高。
学生19:我体会到交流的快乐。大家有不同的方法,彼此交流可以使我们互相学习。
教师:很好!
学生20:相似三角形及其性质有着广泛的应用。
学生21:要灵活的应用相似三角形的知识,应根据具体情况选用不同的方法。晴天时利用物高与影长成比例(包括使用小镜子);阴天时使用手拿刻度尺进行目测,也可以使用小镜子(入射角等于反射角原理得到比例)。
教师:当然,晴天时也可以使用手拿刻度尺进行目测的办法。大家总结的都很好,我们既要注意把现实问题抽象成数学问题,比如构造相似三角形解决一些实际问题。还应注意根据具体情况,(比如晴天与阴天)灵活地选用不同的操作方法。通过今天的学习,你们还有哪些疑惑?
学生20:有些方法我们想不到怎么办?
教师:应该仔细地观察生活,理解题意,分析问题所处的环境,多尝试不同的数学操作活动,探索解决问题的策略;只要多动脑、勤操作,相信同学们一定比我行!(学生鼓掌,教师板书:观察生活——理解题意——分析条件——操作活动)
学生22:利用相似三角形能不能测量其它物体的高?
学生23:可以的,比如树高、电线杆、楼房的高度等。
教师:金字塔是古代埃及的著名建筑,它的底部很大,它的高度是如何测量的?请同学们先阅读课本中的“读一读”内容,再想一想操作活动的办法,下一节课我们再交流。
测量旗杆(或建筑物)的高度,是相似三角形知识应用的一个典型现实问题。从本节课的教学过程,我们可以看到,教师在处理和把握上有如下的特点: 点 评 1、立足于以展示数学活动和合作交流的方式组织教学。
教师首先检查了所安排的活动“不同时刻,身高与影长的比例关系”小组合作的完成情况,从活动经验中得到“在同一时刻,两个物体的高度与它们的影长成比例”这一数学活动事实,并把它应用到求旗杆高度问题中,过渡自然,应用合理。在新课程实施时,我们必需清醒的看到:在基础知识和基本技能游刃有余的背后,隐藏着解决实际问题时数学操作经验缺乏的严重问题。在本节课的教学中,针对各种不同条件下测旗杆高度问题,教师都以组织学生开展数学活动和合作交流为基本的教法和学法。
2、注意培养学生的问题意识。
在数学课堂教学中,我们经常讲“培养学生分析问题和解决问题的能力”,但基本上由教师包办代替了,而“由学生主动的提出问题”基本上做不到。
可以看出,本节课教师在培养学生问题意识中所设计的问题串大致是:
(1)在同一时刻,两个物体的高度与影长有什么关系?
(2)旗杆的高度与人所站的位置有关系吗?为什么?
(3)还有其他测旗杆高的方法吗?为什么?
(4)在没有影子(阴天)的情况下,还能测旗杆高吗?为什么?
(5)如何才能想到多种办法,灵活地解决问题?
在教学过程中有几个闪亮点,如,学生提出了“阴天(没有影子)时,如何测旗杆高?”等问题。 3、培养自主探索、合作交流的学习方法和习惯。
教学中,教师注意发挥学生的主观能动性。在活动中及问题提出后,教师并不急于回答,问题完全由学生自主探索、合作交流去解决,教师只是适时的点拨、引导和补充完善。
