2023-2024学年北师大版九年级上册第一章《特殊平行四边形》跟踪训练(含答案)
文档属性
| 名称 | 2023-2024学年北师大版九年级上册第一章《特殊平行四边形》跟踪训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 54.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-08 23:01:14 | ||
图片预览

文档简介
北师大版2024年九年级上册第一章《特殊平行四边形》跟踪训练
一、选择题
1.正方形具备而菱形不具备的性质是()
A.对角线互相平分 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
2.下列命题是真命题的是()
A.有一个角是直角的四边形是矩形 B.有一组邻边相等的四边形是菱形 C. 有三个角是直角的四边形是矩形 D. 有三条边相等的四边形是菱形
3.从菱形的钝角顶点,向对角的两边条垂线,垂足恰好在该边的中点,则菱形的内角中钝角的度数是()A. B. C. D.
4.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形满足条件的是()
①平行四边形 ②菱形 ③等腰梯形 ④对角线互相垂直的四边形
A.①③ B.②③ C.③④ D.②④
5.在平行四边形、菱形、矩形、正方形中,能够找到一个点,使该点到各顶点距离相等的图形是()
A.平行四边形和菱形 B.菱形和矩形 C.矩形和正方形 D.菱形和正方形
6.矩形的边长为10cm和15cm,其中一个内角的角平分线分长边为两部份,这两部份的长为()A.6cm和9cm B. 5cm和10cm C. 4cm和11cm D. 7cm和8cm
7.如图,点E是正方形ABCD对角线AC上一点,AFBE于点F,交BD于点G,则下述结论中不成立的是()A.AG=BE B.△ABG≌△BCE C.AE=DG D.∠AGD=∠DAG
二、填空题
8.矩形除了具备平行四边形的性质外,还有一些特殊性质:四个角 ,对角线 。
9.在矩形ABCD中,对角线AC、BD交于点O,若,则 。
10.已知菱形一个内角为,且平分这个内角的一条对角线长为8cm,则这个菱形的周长为 。
11.矩形的两条对角线把这个矩形分成了四个 三角形。菱形的两条对角线把这个菱形分成了四个 三角形。正方形的两条对角线把这个正方形分成了四个 三角形。
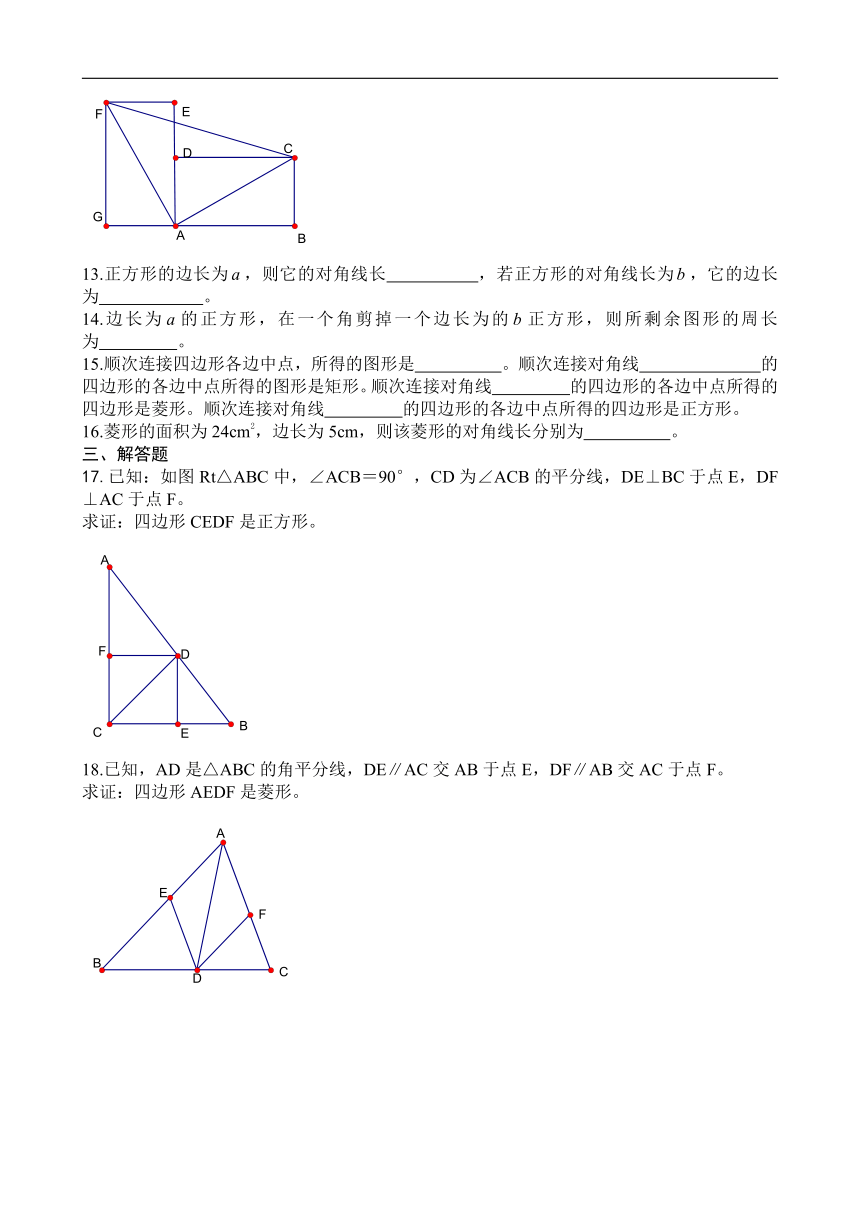
12.如图,把两个大小完全相同的矩形拼成“L”型图案,则 , 。
13.正方形的边长为,则它的对角线长 ,若正方形的对角线长为,它的边长为 。
14.边长为的正方形,在一个角剪掉一个边长为的正方形,则所剩余图形的周长为 。
15.顺次连接四边形各边中点,所得的图形是 。顺次连接对角线 的四边形的各边中点所得的图形是矩形。顺次连接对角线 的四边形的各边中点所得的四边形是菱形。顺次连接对角线 的四边形的各边中点所得的四边形是正方形。
16.菱形的面积为24cm2,边长为5cm,则该菱形的对角线长分别为 。
三、解答题
17.已知:如图Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F。
求证:四边形CEDF是正方形。
18.已知,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F。
求证:四边形AEDF是菱形。
如图,△ABC中,BD、CE是△ABC的两条高,点F、M分别是DE、BC的中点。
求证:FM⊥DE。
20.如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P。
求证:AP=AB。
21.如图,已知点F是正方形ABCD的边BC的中点,CG平分∠DCE,GF⊥AF。
求证:AF=FG。
22.已知中对角线AC的垂直平分线交AD于点F,交BC于点E。
求证:四边形AECF是菱形。
证明:∵EF是AC的垂直平分线(已知)
∴四边形AECF是菱形(对角线互相垂直平分的四边形是菱形)。
老师说小明的解答不正确
⑴你能找出小明错误的原因吗?请你指出来。
⑵请你给出本题的证明过程。
23.请阅读如下材料。
如图,已知正方形ABCD的对角线AC、BD于点O,E是AC上一点,AG⊥BE,垂足为G。求证:OE=OF。
证明:∵四边形ABCD是正方形。
∴∠BOE=∠AOF=90°,且OA=OE.
又∵AG⊥BE,∴∠1+∠3=90°=∠2+∠3,即∠1=∠2.
∴Rt△BOE≌Rt△AOF,∴OE=OF。
⑴根据你的理解,上述证明思路的核心是利用 使问题得以解决,而证明过程中的关键是证出 。
⑵若上述命题改为:点E在AC的延长线上,AG⊥BE交EB的延长线于点G,延长AG交DB的延长线于点F,如图,其他条件不变。
求证:OF=OE.
北师大版2024年九年级上册第一章《特殊平行四边形》跟踪训练
参考答案
一、选择题
1.C 2.C 3.C 4.D 5.C 6.B 7.D
二、填空题
8. 都是直角,相等
9. 40°
10. 32cm
11. 等腰,直角,等腰直角
12. 90°,45°
13. ,
14.
15. 平行四边形,互相垂直,相等,互相垂直且相等
16. 6cm和8cm
三、解答题
17. ∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∠DFC=90°,∠DEC=90°
又∵∠ACB=90°,
∴四边形DECF是矩形,
∴矩形DECF是正方形。
18. ∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EDA=∠FAD,
∵∠EAD=∠FAD,
∴∠EAD=∠EDA,
∴EA=ED,
∴AEDF是菱形。
19.连接MD、ME
∵Rt△CBD中M为BC的中点,
∴MD=BC,
∵Rt△CBE中M为BC的中点,
∴ME=BC,
∴MD=ME,
∵F是DE的中点,
∴FM⊥DE。
20.提示:延长CF、BA交于点M,先证△BCE≌△CDF,得BE=CF。
再证:△CDF≌△AMF得BA=MA,由直角三角形中斜边中线等于斜边的一半,可得Rt△MBP中AP=BM,即AP=AB。
21.提示:取AB的中点M,连接FM,由∠FAM=∠GFC,AM=FC,∠AMF=∠FCG=135°,可证△FAM≌△GFC,即得AF=FG.。
22.⑴小明错在AC和EF并不是互相平分的,EF垂直平分AC,但AC并不平分EF,需要通过证明得出。
⑵∵四边形ABCD是平行四边形,∴∠FAC=∠ECA。
在△AOF与△COE中
∴△AOF≌△COE,∴EO=FO
∴四边形AECF是菱形。
23.⑴三角形全等,∠1=∠2
⑵∵四边形ABCD是正方形,∴∠AOF=∠BOE=90°,且OA=OB,
又∵∠F+∠FAO=90°,∠E+∠FAO=90°,即∠E=∠F
∴Rt△AOF≌Rt△BOE,∴OE=OF.
一、选择题
1.正方形具备而菱形不具备的性质是()
A.对角线互相平分 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
2.下列命题是真命题的是()
A.有一个角是直角的四边形是矩形 B.有一组邻边相等的四边形是菱形 C. 有三个角是直角的四边形是矩形 D. 有三条边相等的四边形是菱形
3.从菱形的钝角顶点,向对角的两边条垂线,垂足恰好在该边的中点,则菱形的内角中钝角的度数是()A. B. C. D.
4.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形满足条件的是()
①平行四边形 ②菱形 ③等腰梯形 ④对角线互相垂直的四边形
A.①③ B.②③ C.③④ D.②④
5.在平行四边形、菱形、矩形、正方形中,能够找到一个点,使该点到各顶点距离相等的图形是()
A.平行四边形和菱形 B.菱形和矩形 C.矩形和正方形 D.菱形和正方形
6.矩形的边长为10cm和15cm,其中一个内角的角平分线分长边为两部份,这两部份的长为()A.6cm和9cm B. 5cm和10cm C. 4cm和11cm D. 7cm和8cm
7.如图,点E是正方形ABCD对角线AC上一点,AFBE于点F,交BD于点G,则下述结论中不成立的是()A.AG=BE B.△ABG≌△BCE C.AE=DG D.∠AGD=∠DAG
二、填空题
8.矩形除了具备平行四边形的性质外,还有一些特殊性质:四个角 ,对角线 。
9.在矩形ABCD中,对角线AC、BD交于点O,若,则 。
10.已知菱形一个内角为,且平分这个内角的一条对角线长为8cm,则这个菱形的周长为 。
11.矩形的两条对角线把这个矩形分成了四个 三角形。菱形的两条对角线把这个菱形分成了四个 三角形。正方形的两条对角线把这个正方形分成了四个 三角形。
12.如图,把两个大小完全相同的矩形拼成“L”型图案,则 , 。
13.正方形的边长为,则它的对角线长 ,若正方形的对角线长为,它的边长为 。
14.边长为的正方形,在一个角剪掉一个边长为的正方形,则所剩余图形的周长为 。
15.顺次连接四边形各边中点,所得的图形是 。顺次连接对角线 的四边形的各边中点所得的图形是矩形。顺次连接对角线 的四边形的各边中点所得的四边形是菱形。顺次连接对角线 的四边形的各边中点所得的四边形是正方形。
16.菱形的面积为24cm2,边长为5cm,则该菱形的对角线长分别为 。
三、解答题
17.已知:如图Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F。
求证:四边形CEDF是正方形。
18.已知,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F。
求证:四边形AEDF是菱形。
如图,△ABC中,BD、CE是△ABC的两条高,点F、M分别是DE、BC的中点。
求证:FM⊥DE。
20.如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P。
求证:AP=AB。
21.如图,已知点F是正方形ABCD的边BC的中点,CG平分∠DCE,GF⊥AF。
求证:AF=FG。
22.已知中对角线AC的垂直平分线交AD于点F,交BC于点E。
求证:四边形AECF是菱形。
证明:∵EF是AC的垂直平分线(已知)
∴四边形AECF是菱形(对角线互相垂直平分的四边形是菱形)。
老师说小明的解答不正确
⑴你能找出小明错误的原因吗?请你指出来。
⑵请你给出本题的证明过程。
23.请阅读如下材料。
如图,已知正方形ABCD的对角线AC、BD于点O,E是AC上一点,AG⊥BE,垂足为G。求证:OE=OF。
证明:∵四边形ABCD是正方形。
∴∠BOE=∠AOF=90°,且OA=OE.
又∵AG⊥BE,∴∠1+∠3=90°=∠2+∠3,即∠1=∠2.
∴Rt△BOE≌Rt△AOF,∴OE=OF。
⑴根据你的理解,上述证明思路的核心是利用 使问题得以解决,而证明过程中的关键是证出 。
⑵若上述命题改为:点E在AC的延长线上,AG⊥BE交EB的延长线于点G,延长AG交DB的延长线于点F,如图,其他条件不变。
求证:OF=OE.
北师大版2024年九年级上册第一章《特殊平行四边形》跟踪训练
参考答案
一、选择题
1.C 2.C 3.C 4.D 5.C 6.B 7.D
二、填空题
8. 都是直角,相等
9. 40°
10. 32cm
11. 等腰,直角,等腰直角
12. 90°,45°
13. ,
14.
15. 平行四边形,互相垂直,相等,互相垂直且相等
16. 6cm和8cm
三、解答题
17. ∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∠DFC=90°,∠DEC=90°
又∵∠ACB=90°,
∴四边形DECF是矩形,
∴矩形DECF是正方形。
18. ∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EDA=∠FAD,
∵∠EAD=∠FAD,
∴∠EAD=∠EDA,
∴EA=ED,
∴AEDF是菱形。
19.连接MD、ME
∵Rt△CBD中M为BC的中点,
∴MD=BC,
∵Rt△CBE中M为BC的中点,
∴ME=BC,
∴MD=ME,
∵F是DE的中点,
∴FM⊥DE。
20.提示:延长CF、BA交于点M,先证△BCE≌△CDF,得BE=CF。
再证:△CDF≌△AMF得BA=MA,由直角三角形中斜边中线等于斜边的一半,可得Rt△MBP中AP=BM,即AP=AB。
21.提示:取AB的中点M,连接FM,由∠FAM=∠GFC,AM=FC,∠AMF=∠FCG=135°,可证△FAM≌△GFC,即得AF=FG.。
22.⑴小明错在AC和EF并不是互相平分的,EF垂直平分AC,但AC并不平分EF,需要通过证明得出。
⑵∵四边形ABCD是平行四边形,∴∠FAC=∠ECA。
在△AOF与△COE中
∴△AOF≌△COE,∴EO=FO
∴四边形AECF是菱形。
23.⑴三角形全等,∠1=∠2
⑵∵四边形ABCD是正方形,∴∠AOF=∠BOE=90°,且OA=OB,
又∵∠F+∠FAO=90°,∠E+∠FAO=90°,即∠E=∠F
∴Rt△AOF≌Rt△BOE,∴OE=OF.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
