人教版五年级上册数学 《植树问题》课件(共26张PPT)
文档属性
| 名称 | 人教版五年级上册数学 《植树问题》课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-07 19:45:13 | ||
图片预览






文档简介
(共26张PPT)
人教版小学数学五年级上册
植树问题
1
2
3
4
5
人民大会堂前有几根柱子?
1
2
3
4
5
6
7
8
9
10
11
12
人民大会堂前有12根柱子。
12根柱子间有几个间隔?
1
2
3
4
5
6
7
8
9
10
11
12根柱子间有11个间隔。
生活中的间隔
间隔
植树问题
(两端都栽)
让我们行动起来吧!
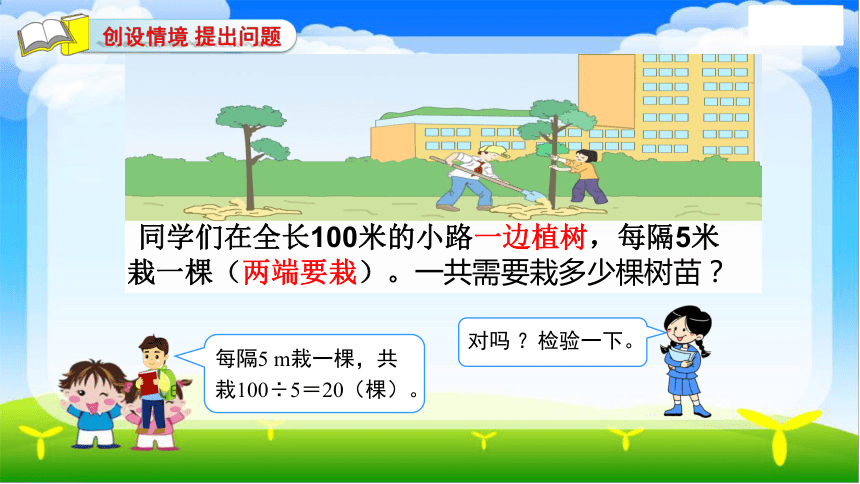
创设情境 提出问题
同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共需要栽多少棵树苗?
创设情境 提出问题
每隔5 m栽一棵,共栽100÷5=20(棵)。
对吗 ?检验一下。
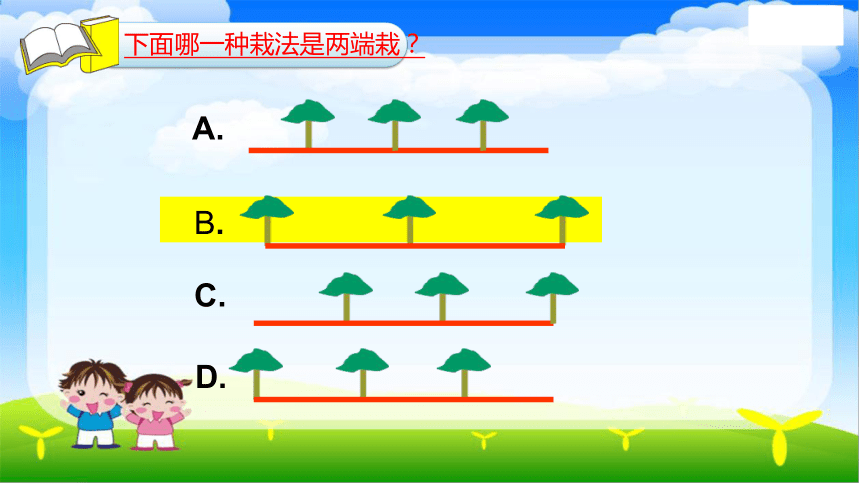
A.
B.
D.
C.
下面哪一种栽法是两端栽?
5米
5米
5米
5米
5米
5米
5米
5米
.......
经历过程 感受方法
100米太长了,可以
先用简单的数试试。
复杂问题
简单问题
发现规律
转化
解决
操作
画图
……
研究方法
如果要在全长20米的小路一边植树。每隔5米栽一棵(两端要栽)。一共需要准备多少棵树苗?
植树
两端要栽
一边
植树
两端要栽
引例
还可以这样画。
探索实践 建立模型
每隔5米种一棵(两端都种) 路长(米) 画一画 间隔数 棵数
10
15
25
30
3
4
6
7
2
3
5
6
同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗?
你能找出
什么规律?
间隔
棵数
段
棵
3
4
4
5
6
7
1
2
3
1
2
3
4
4
5
5
6
6
7
栽的棵数比间隔数多1
探索实践 建立模型
不画图,你能把表格填写完整吗?
你发现了什么规律?
棵数=间隔数+1
探索实践 建立模型
20 米
25 米
距离(米) 间隔数(个) 棵数(棵)
20
25
30
35
4
5
5
6
6
7
7
8
先看看20 m可以栽几棵?
看看25 m可以栽几棵?
植树棵数 间隔数
5
5
7
7
2008
2010
6
8
2009
2009
4
6
在一段直路的一边植树,两端要栽时
探索实践 建立模型
讨论与交流:间隔数都必须靠数数的方法数出来吗?你能根据已知条件通过算术方法列式求出间隔数吗?
你能用算式表示出,当“在一条线路的一侧,两端都要栽”时,植树的“棵数”与“间隔数”有什么关系?
线路一侧 两端都栽
棵数=间隔数+1
间隔数=线路长÷间隔长
建立数学模型
5米
100米
100÷5=20(段)
20+1=21(棵)
答:一共需要栽21棵树苗。
(植树棵数)
(间隔数)
例1 同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗?
运用规律 解决问题
在“植树问题”中,一定要是“树”吗?
除了“树”,还能换成别的事物吗?
思考
摆花篮
装路灯
挂灯笼
摆椅子
公交站点
电线杆
队列
栏杆
楼层
垃圾桶
……
防盗网
斑马线
彩旗
植树问题的应用领域
说一说:
在( )中,( )相当于小树,( )相当于小树之间的间隔。
植树问题的应用领域
运动会上,在一条长200米的笔直跑道的一侧插彩旗(两端都插),每隔10米插一面,一共要插多少面彩旗?
200÷10=20(段)
20+1=21(面)
答:一共要插21面彩旗。
小练笔
广场上的大钟5时敲响5下,8秒敲完。12时敲12下,需要多长时间?
1
2
3
4
5
学以致用 回归生活
8÷(5-1)=2(秒)
2×(12-1)=22(秒)
答:需要22秒。
跟例题相比,有什么不同?
例题是知道了路长求栽树的棵数,
这题是知道了栽树的棵数求路长。
(36-1)×6=210(m)
间隔数
×间隔长度=路长
答:从第1棵到最后一棵的距离是210 m。
逆向思考 拓展新知
6米
………………
一共36棵
预习要求
假如只栽一端或两端都不栽,那又会是什么情形呢?有兴趣的同学可以预习一下数学课本107页例2.
再见
人教版小学数学五年级上册
植树问题
1
2
3
4
5
人民大会堂前有几根柱子?
1
2
3
4
5
6
7
8
9
10
11
12
人民大会堂前有12根柱子。
12根柱子间有几个间隔?
1
2
3
4
5
6
7
8
9
10
11
12根柱子间有11个间隔。
生活中的间隔
间隔
植树问题
(两端都栽)
让我们行动起来吧!
创设情境 提出问题
同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共需要栽多少棵树苗?
创设情境 提出问题
每隔5 m栽一棵,共栽100÷5=20(棵)。
对吗 ?检验一下。
A.
B.
D.
C.
下面哪一种栽法是两端栽?
5米
5米
5米
5米
5米
5米
5米
5米
.......
经历过程 感受方法
100米太长了,可以
先用简单的数试试。
复杂问题
简单问题
发现规律
转化
解决
操作
画图
……
研究方法
如果要在全长20米的小路一边植树。每隔5米栽一棵(两端要栽)。一共需要准备多少棵树苗?
植树
两端要栽
一边
植树
两端要栽
引例
还可以这样画。
探索实践 建立模型
每隔5米种一棵(两端都种) 路长(米) 画一画 间隔数 棵数
10
15
25
30
3
4
6
7
2
3
5
6
同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗?
你能找出
什么规律?
间隔
棵数
段
棵
3
4
4
5
6
7
1
2
3
1
2
3
4
4
5
5
6
6
7
栽的棵数比间隔数多1
探索实践 建立模型
不画图,你能把表格填写完整吗?
你发现了什么规律?
棵数=间隔数+1
探索实践 建立模型
20 米
25 米
距离(米) 间隔数(个) 棵数(棵)
20
25
30
35
4
5
5
6
6
7
7
8
先看看20 m可以栽几棵?
看看25 m可以栽几棵?
植树棵数 间隔数
5
5
7
7
2008
2010
6
8
2009
2009
4
6
在一段直路的一边植树,两端要栽时
探索实践 建立模型
讨论与交流:间隔数都必须靠数数的方法数出来吗?你能根据已知条件通过算术方法列式求出间隔数吗?
你能用算式表示出,当“在一条线路的一侧,两端都要栽”时,植树的“棵数”与“间隔数”有什么关系?
线路一侧 两端都栽
棵数=间隔数+1
间隔数=线路长÷间隔长
建立数学模型
5米
100米
100÷5=20(段)
20+1=21(棵)
答:一共需要栽21棵树苗。
(植树棵数)
(间隔数)
例1 同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗?
运用规律 解决问题
在“植树问题”中,一定要是“树”吗?
除了“树”,还能换成别的事物吗?
思考
摆花篮
装路灯
挂灯笼
摆椅子
公交站点
电线杆
队列
栏杆
楼层
垃圾桶
……
防盗网
斑马线
彩旗
植树问题的应用领域
说一说:
在( )中,( )相当于小树,( )相当于小树之间的间隔。
植树问题的应用领域
运动会上,在一条长200米的笔直跑道的一侧插彩旗(两端都插),每隔10米插一面,一共要插多少面彩旗?
200÷10=20(段)
20+1=21(面)
答:一共要插21面彩旗。
小练笔
广场上的大钟5时敲响5下,8秒敲完。12时敲12下,需要多长时间?
1
2
3
4
5
学以致用 回归生活
8÷(5-1)=2(秒)
2×(12-1)=22(秒)
答:需要22秒。
跟例题相比,有什么不同?
例题是知道了路长求栽树的棵数,
这题是知道了栽树的棵数求路长。
(36-1)×6=210(m)
间隔数
×间隔长度=路长
答:从第1棵到最后一棵的距离是210 m。
逆向思考 拓展新知
6米
………………
一共36棵
预习要求
假如只栽一端或两端都不栽,那又会是什么情形呢?有兴趣的同学可以预习一下数学课本107页例2.
再见
