2023-2024年度合肥市瑶海区八年级上学期数学期末模拟卷一(含答案)
文档属性
| 名称 | 2023-2024年度合肥市瑶海区八年级上学期数学期末模拟卷一(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 284.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 07:58:50 | ||
图片预览




文档简介
2023-2024年度合肥市瑶海区八年级上学期数学期末模拟卷一
姓名: 学号: 考号: 分数: 。
考生须知:
本试卷分试题卷和答题卷两部分,满分150分,考试时间120分钟。
请务必在答题卷上答题,在试题卷上答题是无效的
考试结束后,请将试题卷和答题卷一并交回
一、选择题(每小题4分,有10小题,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若点 在第三象限,则点 在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列四种图形中,对称轴条数最多的是( )
A.等边三角形 B.圆 C.长方形 D.正方形
3.已知三角形的两边长分别为2和3,第三边长是奇数,则第三边长可以是( )
A.1 B.3 C.5 D.9
4.下列各点在函数 的图象上的是( )
A.(1,3) B.(﹣2,4) C.(3,5) D.(﹣1,0)
5.下列个命题中,真命题的个数为( )(1)对顶角相等.(2)经过直线外一点,有且只有一条直线与这条直线平行.(3)在同一平面内,过一点有且只有一条直线与已知直线垂直.(4)两直线平行,同旁内角相等或互补.
A.个 B.个 C.个 D.个
6.如图,表示一次函数的是( )
A. B.
C. D.
7.如图,AE∥BF,∠E=∠F,下列添加的条件不能使△ADE≌△BCF的是( )
A.∠ADE=∠BCF B.DE=CF C.AE=BF D.BD=AC
8.已知∠A=45°15′,∠B=45°12′18″,∠C=45.15°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
9. 如图,△ABC中,AB=AC,点D在线段BC上,,BE⊥DE,若BE=3,则DF=( )
A.7 B. C.6 D.
10.如图,在同一平面直角坐标系中,一次函数与,小聪根据图象得到如下结论:
①;②关于x,y的方程组的解为;③关于x的方程的解为;④关于x的不等式的解集是.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题5分,共4小题,共20分)
11.在函数中,自变量x的取值范围是 .
12.已知三角形的三边分别为2,x,3,那么x的取值范围是
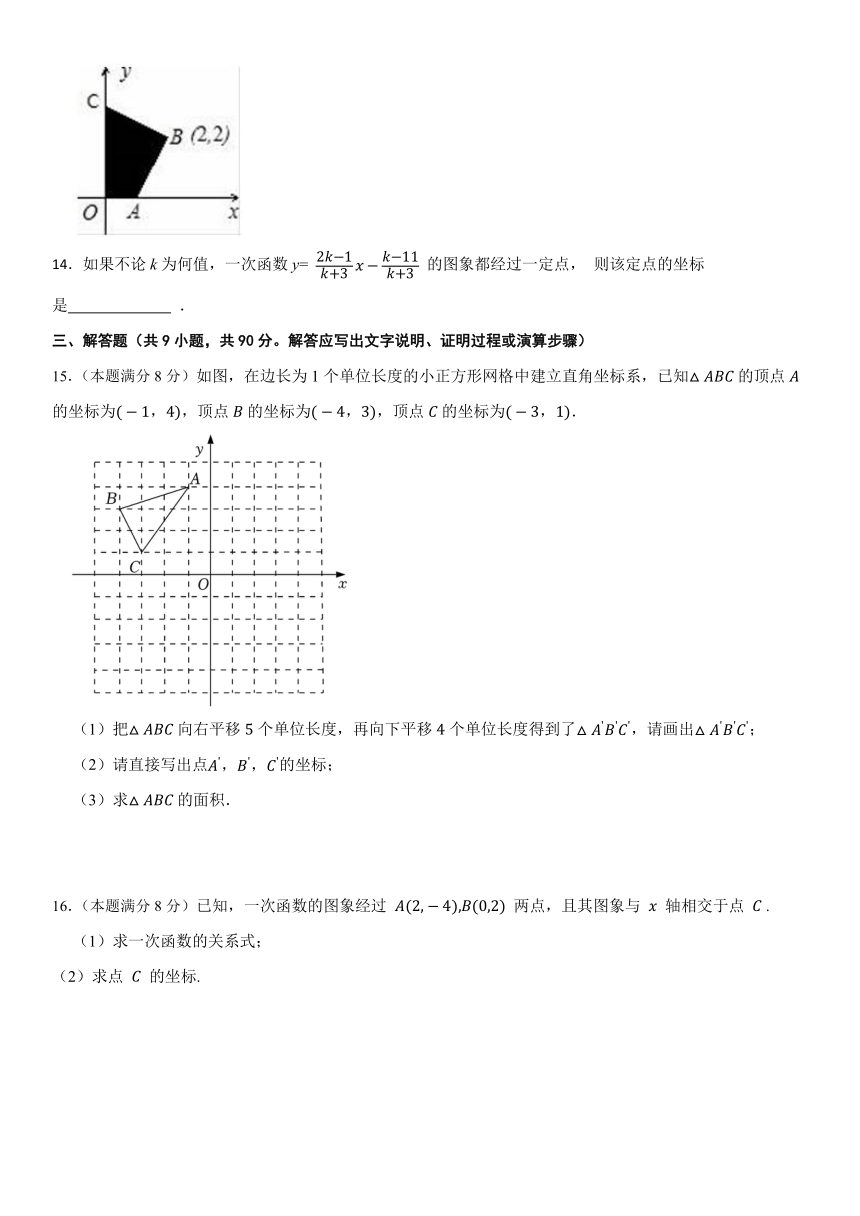
13.如图,BC⊥AB,则图中阴影部分的面积为 .
14.如果不论k为何值,一次函数y= 的图象都经过一定点, 则该定点的坐标是 .
三、解答题(共9小题,共90分。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分8分)如图,在边长为1个单位长度的小正方形网格中建立直角坐标系,已知的顶点的坐标为,,顶点的坐标为,,顶点的坐标为,.
(1)把向右平移个单位长度,再向下平移个单位长度得到了,请画出;
(2)请直接写出点的坐标;
(3)求的面积.
16.(本题满分8分)已知,一次函数的图象经过 两点,且其图象与 轴相交于点 .
(1)求一次函数的关系式;
(2)求点 的坐标.
17.(本题满分8分)如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC.
.
18.(本题满分8分)在平面直角坐标系中,一次函数的图象与函数的图象平行,且经过点.
(1)求这个一次函数的解析式;
(2)当时,对于x的每一个值,函数的值大于一次函数的值,直接写出m的取值范围.
19.(本题满分10分)如图所示,四边形ABCD的对角线AC与BD相交于O点,
(1)若∠1=∠2,∠3=∠4,求证:△ABC≌△ADC;
(2)若∠1=∠2,∠ABO=∠ADO,求证:BO=DO
20.(本题满分10分)如图,在△ABC中,AB=AC,∠B=30°,D为BC边上一点,∠DAB=45°.
(1)求∠DAC的度数;
(2)请说明:AB=CD.
21.(本题满分12分)某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200千瓦时时,按0.6元/千瓦时计费;月用电量超过200千瓦时时,其中的200千瓦时仍按0.6元/千瓦时计费,超过部分按0.65元/千瓦时计费设每户家庭的月用电量为x千瓦时时,应交电费y元
(1)当月用电量不超过200千瓦时时,y与x的函数关系式为 ;
当月用电量超过200千瓦时时,y与x的函数关系式为 .
(2)小新家十月份的用电量为160千瓦时,求他家十月份应交电费多少元.
(3)小明家十月份交电费146元,求他家十月份用电多少千瓦时.
22.(本题满分12分)如图,在△ABC中,高线AD,BE,相交于点O,AE=BE,BD=2,DC=2BD.
(1)证明:△AEO≌△BEC;
(2)求OA的长;
(3)F是直线AC上的一点,且CF=BO,动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发,沿射线BC以每秒4个单位长度的速度运动,P,Q两点同时出发,当点P到达A点时,P,Q两点同时停止运动,设点P的运动时间为t秒,则是否存在t值,使得以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等?若存在,请求出符合条件的t值,若不存在,请说明理由.
23.(本题满分14分)如图,在平面直角坐标系中,直线分别与轴,轴交于点,,过点作轴的垂线,与直线交于点.
(1)求点的坐标;
(2)点是线段上一动点,直线与轴交于点.
若的面积为,求点的坐标;
如图,当点在轴正半轴上时,将直线绕点逆时针旋转后的直线与线段交于点,连接,若,求线段的长.
2023-2024年度合肥市瑶海区八年级秋学期数学期末模拟卷一参考答案
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】且
12.【答案】1<x<5
13.【答案】4
14.【答案】(2,3)
15.【答案】(1)解:如图所示,即为所求;
(2)解:
(3)解:的面积=正方形面积-边上三块小三角形的面积,.
答:的面积是3.5.
16.【答案】(1)设一次函数的解析式为y=kx+b,
∵一次函数的图象经过 两点
∴ ,
解得 .
∴一次函数的解析式为y=-3x+2.
(2)当y=0时,0=-3x+2
∴
∴C
17.【答案】证明:∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,∴DE=DF;∵DE⊥AB于E,DF⊥AC于F.∴在Rt△DBE和Rt△DCF中∴Rt△DBE≌Rt△DCF(HL);∴EB=FC.
18.【答案】(1)解:一次函数的图象与函数的图象平行,
.
把点代入,得到.
这个一次函数的解析式为.
(2)解:
19.【答案】(1)证明:在△ABC 和△ADC 中
∴△ABC △ADC(ASA)
(2)证明: 在△AOB 和△AOD 中
∴△AOB △AOD(AAS)
∴BO=DO
20.【答案】(1)解:∵AB=AC,
∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;
(2)证明:∵∠DAB=45°,
∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∵AB=AC,
∴AB=CD.
21.【答案】(1);
(2)解:因为160<200,
所以y=0.6×160=96(元).
答:小新家十月份应交电费96元
(3)解:因为小明家十月份的电费超过了120元,所以用电量超过了200千瓦时.
把y=146代入中,
得x=240.
答:小明家十月份用电240千瓦时
22.【答案】(1)证明:∵AD,BE是的高,
∴,
∵,
∴,
在和中,
,
∴ (ASA);
(2)解:∵,,
∴,
∴,
∵,
∴;
故答案为:6.
(3)解:存在,理由如下:
解:由题意得,,,
∵,
∴,
如图所示,
当时,OP=CQ,
∴,
解得:;
如图所示,
当时,OP=CQ,
∴,
解得:,
综上所述,存在,当秒或2秒时,以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等.
23.【答案】(1)解:分别与轴,轴交于点,,
,
解得:,
,
时,,
;
(2)解:Ⅰ解:在线段上,且,,
设点,
分两种情况:
当在轴正半轴上时,如图:
,,,轴,
,
,
,
,
即:,
,
;
当在轴负半轴上时,如图:
点,,,,
,
,
,
,
解得:,
;
综上所述:或.
过作垂直于轴,垂足为,过作的垂线交轴于点,
,,
,
在与中,
,
≌,
,,
在与中,
,
≌,
,
又,,
,
,
,
设,则,
在中,,
,
,
.
姓名: 学号: 考号: 分数: 。
考生须知:
本试卷分试题卷和答题卷两部分,满分150分,考试时间120分钟。
请务必在答题卷上答题,在试题卷上答题是无效的
考试结束后,请将试题卷和答题卷一并交回
一、选择题(每小题4分,有10小题,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若点 在第三象限,则点 在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列四种图形中,对称轴条数最多的是( )
A.等边三角形 B.圆 C.长方形 D.正方形
3.已知三角形的两边长分别为2和3,第三边长是奇数,则第三边长可以是( )
A.1 B.3 C.5 D.9
4.下列各点在函数 的图象上的是( )
A.(1,3) B.(﹣2,4) C.(3,5) D.(﹣1,0)
5.下列个命题中,真命题的个数为( )(1)对顶角相等.(2)经过直线外一点,有且只有一条直线与这条直线平行.(3)在同一平面内,过一点有且只有一条直线与已知直线垂直.(4)两直线平行,同旁内角相等或互补.
A.个 B.个 C.个 D.个
6.如图,表示一次函数的是( )
A. B.
C. D.
7.如图,AE∥BF,∠E=∠F,下列添加的条件不能使△ADE≌△BCF的是( )
A.∠ADE=∠BCF B.DE=CF C.AE=BF D.BD=AC
8.已知∠A=45°15′,∠B=45°12′18″,∠C=45.15°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
9. 如图,△ABC中,AB=AC,点D在线段BC上,,BE⊥DE,若BE=3,则DF=( )
A.7 B. C.6 D.
10.如图,在同一平面直角坐标系中,一次函数与,小聪根据图象得到如下结论:
①;②关于x,y的方程组的解为;③关于x的方程的解为;④关于x的不等式的解集是.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题5分,共4小题,共20分)
11.在函数中,自变量x的取值范围是 .
12.已知三角形的三边分别为2,x,3,那么x的取值范围是
13.如图,BC⊥AB,则图中阴影部分的面积为 .
14.如果不论k为何值,一次函数y= 的图象都经过一定点, 则该定点的坐标是 .
三、解答题(共9小题,共90分。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分8分)如图,在边长为1个单位长度的小正方形网格中建立直角坐标系,已知的顶点的坐标为,,顶点的坐标为,,顶点的坐标为,.
(1)把向右平移个单位长度,再向下平移个单位长度得到了,请画出;
(2)请直接写出点的坐标;
(3)求的面积.
16.(本题满分8分)已知,一次函数的图象经过 两点,且其图象与 轴相交于点 .
(1)求一次函数的关系式;
(2)求点 的坐标.
17.(本题满分8分)如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC.
.
18.(本题满分8分)在平面直角坐标系中,一次函数的图象与函数的图象平行,且经过点.
(1)求这个一次函数的解析式;
(2)当时,对于x的每一个值,函数的值大于一次函数的值,直接写出m的取值范围.
19.(本题满分10分)如图所示,四边形ABCD的对角线AC与BD相交于O点,
(1)若∠1=∠2,∠3=∠4,求证:△ABC≌△ADC;
(2)若∠1=∠2,∠ABO=∠ADO,求证:BO=DO
20.(本题满分10分)如图,在△ABC中,AB=AC,∠B=30°,D为BC边上一点,∠DAB=45°.
(1)求∠DAC的度数;
(2)请说明:AB=CD.
21.(本题满分12分)某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200千瓦时时,按0.6元/千瓦时计费;月用电量超过200千瓦时时,其中的200千瓦时仍按0.6元/千瓦时计费,超过部分按0.65元/千瓦时计费设每户家庭的月用电量为x千瓦时时,应交电费y元
(1)当月用电量不超过200千瓦时时,y与x的函数关系式为 ;
当月用电量超过200千瓦时时,y与x的函数关系式为 .
(2)小新家十月份的用电量为160千瓦时,求他家十月份应交电费多少元.
(3)小明家十月份交电费146元,求他家十月份用电多少千瓦时.
22.(本题满分12分)如图,在△ABC中,高线AD,BE,相交于点O,AE=BE,BD=2,DC=2BD.
(1)证明:△AEO≌△BEC;
(2)求OA的长;
(3)F是直线AC上的一点,且CF=BO,动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发,沿射线BC以每秒4个单位长度的速度运动,P,Q两点同时出发,当点P到达A点时,P,Q两点同时停止运动,设点P的运动时间为t秒,则是否存在t值,使得以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等?若存在,请求出符合条件的t值,若不存在,请说明理由.
23.(本题满分14分)如图,在平面直角坐标系中,直线分别与轴,轴交于点,,过点作轴的垂线,与直线交于点.
(1)求点的坐标;
(2)点是线段上一动点,直线与轴交于点.
若的面积为,求点的坐标;
如图,当点在轴正半轴上时,将直线绕点逆时针旋转后的直线与线段交于点,连接,若,求线段的长.
2023-2024年度合肥市瑶海区八年级秋学期数学期末模拟卷一参考答案
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】且
12.【答案】1<x<5
13.【答案】4
14.【答案】(2,3)
15.【答案】(1)解:如图所示,即为所求;
(2)解:
(3)解:的面积=正方形面积-边上三块小三角形的面积,.
答:的面积是3.5.
16.【答案】(1)设一次函数的解析式为y=kx+b,
∵一次函数的图象经过 两点
∴ ,
解得 .
∴一次函数的解析式为y=-3x+2.
(2)当y=0时,0=-3x+2
∴
∴C
17.【答案】证明:∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,∴DE=DF;∵DE⊥AB于E,DF⊥AC于F.∴在Rt△DBE和Rt△DCF中∴Rt△DBE≌Rt△DCF(HL);∴EB=FC.
18.【答案】(1)解:一次函数的图象与函数的图象平行,
.
把点代入,得到.
这个一次函数的解析式为.
(2)解:
19.【答案】(1)证明:在△ABC 和△ADC 中
∴△ABC △ADC(ASA)
(2)证明: 在△AOB 和△AOD 中
∴△AOB △AOD(AAS)
∴BO=DO
20.【答案】(1)解:∵AB=AC,
∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;
(2)证明:∵∠DAB=45°,
∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∵AB=AC,
∴AB=CD.
21.【答案】(1);
(2)解:因为160<200,
所以y=0.6×160=96(元).
答:小新家十月份应交电费96元
(3)解:因为小明家十月份的电费超过了120元,所以用电量超过了200千瓦时.
把y=146代入中,
得x=240.
答:小明家十月份用电240千瓦时
22.【答案】(1)证明:∵AD,BE是的高,
∴,
∵,
∴,
在和中,
,
∴ (ASA);
(2)解:∵,,
∴,
∴,
∵,
∴;
故答案为:6.
(3)解:存在,理由如下:
解:由题意得,,,
∵,
∴,
如图所示,
当时,OP=CQ,
∴,
解得:;
如图所示,
当时,OP=CQ,
∴,
解得:,
综上所述,存在,当秒或2秒时,以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等.
23.【答案】(1)解:分别与轴,轴交于点,,
,
解得:,
,
时,,
;
(2)解:Ⅰ解:在线段上,且,,
设点,
分两种情况:
当在轴正半轴上时,如图:
,,,轴,
,
,
,
,
即:,
,
;
当在轴负半轴上时,如图:
点,,,,
,
,
,
,
解得:,
;
综上所述:或.
过作垂直于轴,垂足为,过作的垂线交轴于点,
,,
,
在与中,
,
≌,
,,
在与中,
,
≌,
,
又,,
,
,
,
设,则,
在中,,
,
,
.
同课章节目录
