3.2探索活动:2,5的倍数的特征同步练习五年级数学上册北师大版(含解析)
文档属性
| 名称 | 3.2探索活动:2,5的倍数的特征同步练习五年级数学上册北师大版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 115.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-07 20:20:29 | ||
图片预览


文档简介
3.2 探索活动:2,5 的倍数的特征(同步练习)
一、填空题
1 .用 0 ,1 ,3 ,4 组成一个四位数,若它是 2 的倍数,这个数最小是 .
2 .个位上是 的数,都是 2 的倍数.(从小到大填写)
3 .一个五位数,十位上的数字是最小的合数,百位上的数字是最小的质数,千位上的
数字是最小的自然数.如果这个数能被 2 和 5 整除,这个数最小的是 .
4 .一个数(大于 0)既是 2 的倍数又是 5 的倍数,这个数的个位数必定是 .
二、判断题
5 .一个奇数与 5 相乘,结果是偶数。 ( )
6 .任何偶数加上 1 后都是奇数。 ( )
7 .奇数乘以一个自然数,积一定是奇数。 ( )
三、选择题
8 .非 0 自然数按是不是 2 的倍数来分,分为( ) .
A .倍数与因数 B .奇数与偶数
C .质数与合数、 0 和 1 D .正数与负数
9 .一个奇数应该怎样计算,结果还是奇数( )。
A .加上 2 B .乘 2 C .除以 2
10 .13 的倍数是( )
A .奇数 B .偶数 C .奇数或偶数
11 .8 个奇数相加,和一定是( )。
A .奇数 B .偶数 C .质数
四、解答题
12 .一个数在 100 以内,并且比 24 的倍数多 15,这个数最大是多少?
13 .李伯伯家的一棵石榴树收获了 76 个石榴,他每 5 个装一袋,能正好装完吗?每 2
个装一袋,能正好装完吗?为什么?
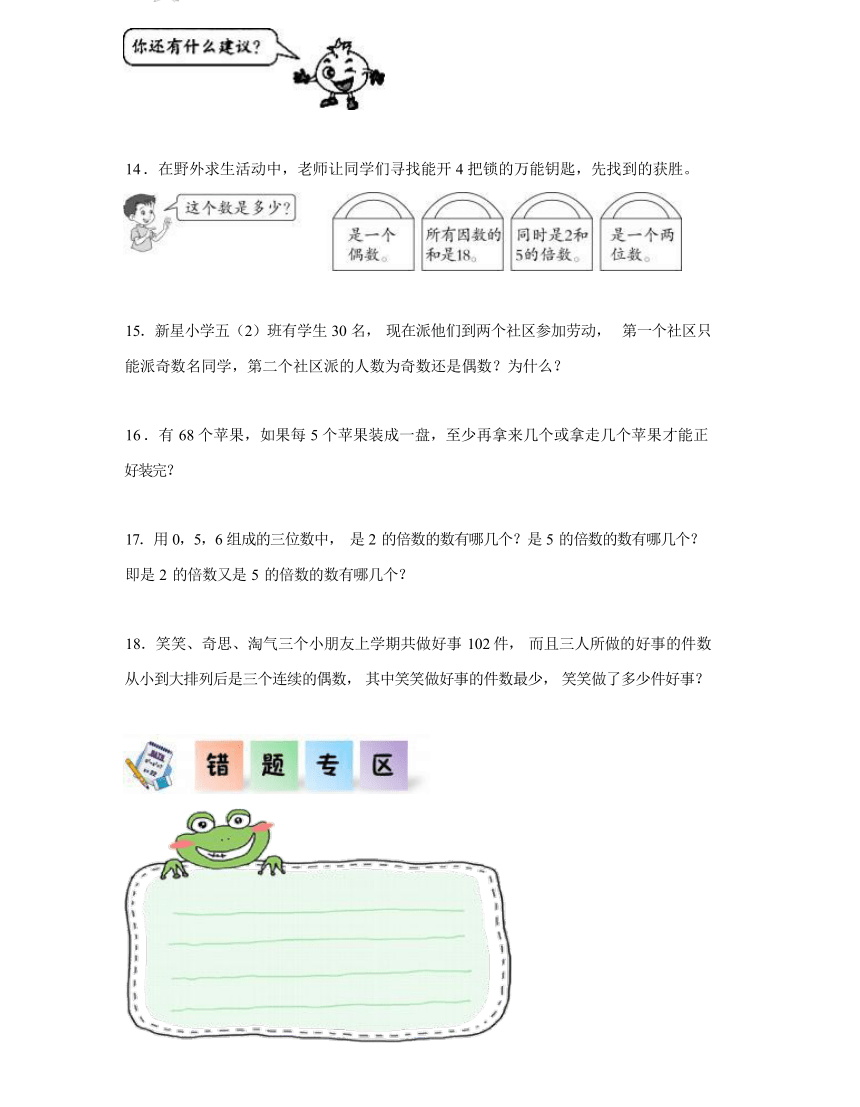
14 .在野外求生活动中,老师让同学们寻找能开 4 把锁的万能钥匙,先找到的获胜。
15.新星小学五(2)班有学生 30 名, 现在派他们到两个社区参加劳动, 第一个社区只
能派奇数名同学,第二个社区派的人数为奇数还是偶数?为什么?
16 .有 68 个苹果,如果每 5 个苹果装成一盘,至少再拿来几个或拿走几个苹果才能正
好装完?
17.用 0,5,6 组成的三位数中, 是 2 的倍数的数有哪几个?是 5 的倍数的数有哪几个?
即是 2 的倍数又是 5 的倍数的数有哪几个?
18.笑笑、奇思、淘气三个小朋友上学期共做好事 102 件, 而且三人所做的好事的件数
从小到大排列后是三个连续的偶数, 其中笑笑做好事的件数最少, 笑笑做了多少件好事?
1 .1034
【详解】试题分析:根据 2 的倍数的特点知:个位上的数是 0 、2 、4 、6 、8;0<1<3<4, 求组成的最小的数, 该数从最高位到最低位, 数字选择由小到大, 但最高位上的数字不能为
0 .所以最高位上是 1,个位上必须是 4,所以这个数最小是 1034 .
解:用 0 ,1 ,3 ,4 组成一个四位数,若它是 2 的倍数,这个数最小是 1034,
故答案为 1034 .
点评:本题主要考查 2 的倍数特征,解答此题整数的组成,求组成的最大的数,该数从最高 位到最低位,数字选择由大到小;求组成的最小的数,该数从最高位到最低位,数字选择由
小到大,但最高位上的数字不能为 0 .
2 .0,2,4,6,8
3 .11240
【详解】试题分析:十位上的数字是最小的合数,最小的合数是 4,百位上的数字是最小的 质数,最小的质数是 2,千位上的数字是最小的自然数.最小的自然数是 1,因为是五位数, 并且要求的是这个数最小的是多少, 所以该五位数是最高位(万位是 1),因为这个数能被 2
和 5 整除,所以该数个位为 0;进而写出即可.
解:由分析知:该五位数十位数字是 4,百位上的数字 2,千位上的数字是 1,万位上的数
字是 1,个位上的数字是 0,即该五位数是 11240;
故答案为 11240 .
点评:解答此题的关键是:应明确最小是合数、最小的质数、最小的自然数分别是几,进而
根据能被 2 、5 整除数的特征,进行解答即可.
4 .0
【详解】试题分析:根据 2 、5 倍数的特征可知:这个数的个位上必需是 0,因为个位上是 0
的数同时是 2 和 5 的倍数,依此即可求解.
解:因为一个数(大于 0)既是 2 的倍数又是 5 的倍数,所以这个数的个位数必定是 0 .
故答案为 0 .
点评:此题考查了 2 、5 倍数的特征,个位上是 0 的数满足同时是 2 和 5 的倍数.
5 . ×
【分析】根据奇数和偶数的定义:自然数中,是 2 的倍数的数叫偶数,不是 2 的倍数的数叫
奇数;再根据奇数和偶数的性质:奇数与奇数的积是奇数,偶数与偶数的积是偶数,奇数和
偶数的积是偶数对此题进行判断即可。
【详解】5 不是 2 的倍数,所以 5 是奇数,
一个奇数与 5 相乘,即一个奇数和一个奇数相乘,结果是奇数。
故答案为: ×
【点睛】本题考查了对奇数和偶数概念以及性质的掌握, 记忆的同时要会灵活运用是解题的
关键。
6 . √
【分析】整数中, 是 2 的倍数的数叫偶数, 不是 2 的倍数的数叫奇数。最小的偶数是 0,没
有最大的偶数,最小的奇数是 1,也没有最大的奇数。根据此进行判断即可。
【详解】由分析可得:
任何一个偶数,加上 1 后,都不再是 2 的倍数,而是奇数。
所以任何偶数加上 1 后都是奇数。
故答案为: √
【点睛】本题考查了奇数和偶数的概念,熟悉概念的同时也要会结合题目灵活运用。
7 . ×
【分析】根据奇数和偶数的运算性质进行判断即可解答。
【详解】因为奇数 ×奇数=奇数;奇数×偶数=偶数,所以奇数乘以一个自然数,积不一定
是奇数。
故答案为: ×。
【点睛】此题主要考查学生对奇数偶数运算性质的理解与掌握。
8 .B
9 .A
【分析】根据奇数+偶数=奇数,进行分析。
【详解】2 是偶数。
A.奇数+2=奇数;
B.奇数×2=偶数;
C.奇数÷2=小数。
故答案为: A
【点睛】2 的倍数叫偶数,不是 2 的倍数叫奇数。
10 .C
【详解】试题分析:根据奇数和偶数的含义:自然数中,是 2 的倍数的数叫做偶数,不是 2 的倍数的数叫做奇数;因为 13 是奇数,根据:奇数×偶数=偶数,奇数×奇数=奇数;可以得
出 13 的倍数是奇数或偶数;据此选择即可.
解:因为 13 是奇数,根据:奇数×偶数=偶数,奇数×奇数=奇数;可以得出 13 的倍数是奇
数或偶数;
故选 C .
点评:解答此题应根据数的奇偶性特点进行解答;也可以通过举例进行验证,得出结论.
11 .B
【分析】根据奇数、偶数的性质:两个偶数的和或差仍是偶数, 两个奇数的和或差也是偶数,
奇数和偶数的和或差是奇数;由此解答即可。
【详解】由分析知:两个奇数和一定是偶数,所以偶数个奇数相加的和一定是偶数
【点睛】本题考查学生对理解偶数与奇数的意义以及奇数和偶数的性质的认知。
12 .87
【详解】24×4+15 =111 111>100 24×3+15 =87
答:这个数最大是 87 .
通过两个条件来找这个数,这个数“ 比 24 的倍数多 15” ,“在 100 以内” ,用尝试的方法,从 多倍数往下减小.这个数不会是 24 的 4 倍,因为 24×4+15 =111,超过 100 了,那么用 3
倍再试, 24×3+15 =87,求这个数最大时多少,所以 87 符合要求.
13 .每 5 个装一袋,不能正好装完;每 2 个装一袋,能正好装完.因为 76 不是 5 的倍数, 是 2 的倍数.还可以一部分每 5 个装一袋,另一部分每 2 个装一袋,如:每 5 个装一袋,
装 14 袋, 一共装 70 个,余下 6 个每 2 个装一袋,装 3 袋.
14 .10
15 .奇数,因为奇数+奇数=偶数。
【分析】根据题意,总人数 30 是偶数,根据奇数和偶数的性质,奇数+奇数=偶数,奇数 +偶数=奇数, 第一个社区只能派奇数名同学, 那么第二个社区必须是奇数, 因为奇数加奇
数才是偶数,据此解答。
【详解】新星小学五(2)班有学生 30 名, 总人数是偶数。若第一个社区只能派奇数名同学,
第二个社区派的人数为奇数,因为奇数+奇数=偶数。
答:第二个社区派的人数是奇数,因为奇数+奇数=偶数。
【点睛】本题考查了奇数和偶数的运算性质, 本题关键是根据奇数+奇数=偶数, 奇数+偶
数=奇数来判断。
16 .2 个; 3 个
【分析】每 5 个苹果装成一盘,则苹果的个数是 5 的人倍数,由 5 的倍数的特征:个位是 0
或 5 的数是 5 的倍数可知, 70 和 65 是 5 的倍数由此解答。
【详解】70-68 =2(个)
68-65 =3(个)
答:至少再拿来 2 个或拿走 3 个苹果才能正好装完。
【点睛】本题主要考查 5 的倍数特征的应用, 理解“至少再拿来几个或拿走几个”是解题的关
键。
17 .2 的倍数有: 560 、506 、650
5 的倍数有 560 、650 、605
同时是 2 和 5 的倍数有: 560 、650
18 .32 件
【分析】由于每相邻的两个偶数相差 2,所以三个连续偶数的和是中间偶数的 3 倍, 由此求
出中间偶数,再减去 2 即可。
【详解】 102÷3-2
=34-2
=32(件)
答:笑笑做了 32 件好事。
【点睛】本题主要考查连续偶数的特征,解题时要明确每相邻的两个偶数相差 2。
一、填空题
1 .用 0 ,1 ,3 ,4 组成一个四位数,若它是 2 的倍数,这个数最小是 .
2 .个位上是 的数,都是 2 的倍数.(从小到大填写)
3 .一个五位数,十位上的数字是最小的合数,百位上的数字是最小的质数,千位上的
数字是最小的自然数.如果这个数能被 2 和 5 整除,这个数最小的是 .
4 .一个数(大于 0)既是 2 的倍数又是 5 的倍数,这个数的个位数必定是 .
二、判断题
5 .一个奇数与 5 相乘,结果是偶数。 ( )
6 .任何偶数加上 1 后都是奇数。 ( )
7 .奇数乘以一个自然数,积一定是奇数。 ( )
三、选择题
8 .非 0 自然数按是不是 2 的倍数来分,分为( ) .
A .倍数与因数 B .奇数与偶数
C .质数与合数、 0 和 1 D .正数与负数
9 .一个奇数应该怎样计算,结果还是奇数( )。
A .加上 2 B .乘 2 C .除以 2
10 .13 的倍数是( )
A .奇数 B .偶数 C .奇数或偶数
11 .8 个奇数相加,和一定是( )。
A .奇数 B .偶数 C .质数
四、解答题
12 .一个数在 100 以内,并且比 24 的倍数多 15,这个数最大是多少?
13 .李伯伯家的一棵石榴树收获了 76 个石榴,他每 5 个装一袋,能正好装完吗?每 2
个装一袋,能正好装完吗?为什么?
14 .在野外求生活动中,老师让同学们寻找能开 4 把锁的万能钥匙,先找到的获胜。
15.新星小学五(2)班有学生 30 名, 现在派他们到两个社区参加劳动, 第一个社区只
能派奇数名同学,第二个社区派的人数为奇数还是偶数?为什么?
16 .有 68 个苹果,如果每 5 个苹果装成一盘,至少再拿来几个或拿走几个苹果才能正
好装完?
17.用 0,5,6 组成的三位数中, 是 2 的倍数的数有哪几个?是 5 的倍数的数有哪几个?
即是 2 的倍数又是 5 的倍数的数有哪几个?
18.笑笑、奇思、淘气三个小朋友上学期共做好事 102 件, 而且三人所做的好事的件数
从小到大排列后是三个连续的偶数, 其中笑笑做好事的件数最少, 笑笑做了多少件好事?
1 .1034
【详解】试题分析:根据 2 的倍数的特点知:个位上的数是 0 、2 、4 、6 、8;0<1<3<4, 求组成的最小的数, 该数从最高位到最低位, 数字选择由小到大, 但最高位上的数字不能为
0 .所以最高位上是 1,个位上必须是 4,所以这个数最小是 1034 .
解:用 0 ,1 ,3 ,4 组成一个四位数,若它是 2 的倍数,这个数最小是 1034,
故答案为 1034 .
点评:本题主要考查 2 的倍数特征,解答此题整数的组成,求组成的最大的数,该数从最高 位到最低位,数字选择由大到小;求组成的最小的数,该数从最高位到最低位,数字选择由
小到大,但最高位上的数字不能为 0 .
2 .0,2,4,6,8
3 .11240
【详解】试题分析:十位上的数字是最小的合数,最小的合数是 4,百位上的数字是最小的 质数,最小的质数是 2,千位上的数字是最小的自然数.最小的自然数是 1,因为是五位数, 并且要求的是这个数最小的是多少, 所以该五位数是最高位(万位是 1),因为这个数能被 2
和 5 整除,所以该数个位为 0;进而写出即可.
解:由分析知:该五位数十位数字是 4,百位上的数字 2,千位上的数字是 1,万位上的数
字是 1,个位上的数字是 0,即该五位数是 11240;
故答案为 11240 .
点评:解答此题的关键是:应明确最小是合数、最小的质数、最小的自然数分别是几,进而
根据能被 2 、5 整除数的特征,进行解答即可.
4 .0
【详解】试题分析:根据 2 、5 倍数的特征可知:这个数的个位上必需是 0,因为个位上是 0
的数同时是 2 和 5 的倍数,依此即可求解.
解:因为一个数(大于 0)既是 2 的倍数又是 5 的倍数,所以这个数的个位数必定是 0 .
故答案为 0 .
点评:此题考查了 2 、5 倍数的特征,个位上是 0 的数满足同时是 2 和 5 的倍数.
5 . ×
【分析】根据奇数和偶数的定义:自然数中,是 2 的倍数的数叫偶数,不是 2 的倍数的数叫
奇数;再根据奇数和偶数的性质:奇数与奇数的积是奇数,偶数与偶数的积是偶数,奇数和
偶数的积是偶数对此题进行判断即可。
【详解】5 不是 2 的倍数,所以 5 是奇数,
一个奇数与 5 相乘,即一个奇数和一个奇数相乘,结果是奇数。
故答案为: ×
【点睛】本题考查了对奇数和偶数概念以及性质的掌握, 记忆的同时要会灵活运用是解题的
关键。
6 . √
【分析】整数中, 是 2 的倍数的数叫偶数, 不是 2 的倍数的数叫奇数。最小的偶数是 0,没
有最大的偶数,最小的奇数是 1,也没有最大的奇数。根据此进行判断即可。
【详解】由分析可得:
任何一个偶数,加上 1 后,都不再是 2 的倍数,而是奇数。
所以任何偶数加上 1 后都是奇数。
故答案为: √
【点睛】本题考查了奇数和偶数的概念,熟悉概念的同时也要会结合题目灵活运用。
7 . ×
【分析】根据奇数和偶数的运算性质进行判断即可解答。
【详解】因为奇数 ×奇数=奇数;奇数×偶数=偶数,所以奇数乘以一个自然数,积不一定
是奇数。
故答案为: ×。
【点睛】此题主要考查学生对奇数偶数运算性质的理解与掌握。
8 .B
9 .A
【分析】根据奇数+偶数=奇数,进行分析。
【详解】2 是偶数。
A.奇数+2=奇数;
B.奇数×2=偶数;
C.奇数÷2=小数。
故答案为: A
【点睛】2 的倍数叫偶数,不是 2 的倍数叫奇数。
10 .C
【详解】试题分析:根据奇数和偶数的含义:自然数中,是 2 的倍数的数叫做偶数,不是 2 的倍数的数叫做奇数;因为 13 是奇数,根据:奇数×偶数=偶数,奇数×奇数=奇数;可以得
出 13 的倍数是奇数或偶数;据此选择即可.
解:因为 13 是奇数,根据:奇数×偶数=偶数,奇数×奇数=奇数;可以得出 13 的倍数是奇
数或偶数;
故选 C .
点评:解答此题应根据数的奇偶性特点进行解答;也可以通过举例进行验证,得出结论.
11 .B
【分析】根据奇数、偶数的性质:两个偶数的和或差仍是偶数, 两个奇数的和或差也是偶数,
奇数和偶数的和或差是奇数;由此解答即可。
【详解】由分析知:两个奇数和一定是偶数,所以偶数个奇数相加的和一定是偶数
【点睛】本题考查学生对理解偶数与奇数的意义以及奇数和偶数的性质的认知。
12 .87
【详解】24×4+15 =111 111>100 24×3+15 =87
答:这个数最大是 87 .
通过两个条件来找这个数,这个数“ 比 24 的倍数多 15” ,“在 100 以内” ,用尝试的方法,从 多倍数往下减小.这个数不会是 24 的 4 倍,因为 24×4+15 =111,超过 100 了,那么用 3
倍再试, 24×3+15 =87,求这个数最大时多少,所以 87 符合要求.
13 .每 5 个装一袋,不能正好装完;每 2 个装一袋,能正好装完.因为 76 不是 5 的倍数, 是 2 的倍数.还可以一部分每 5 个装一袋,另一部分每 2 个装一袋,如:每 5 个装一袋,
装 14 袋, 一共装 70 个,余下 6 个每 2 个装一袋,装 3 袋.
14 .10
15 .奇数,因为奇数+奇数=偶数。
【分析】根据题意,总人数 30 是偶数,根据奇数和偶数的性质,奇数+奇数=偶数,奇数 +偶数=奇数, 第一个社区只能派奇数名同学, 那么第二个社区必须是奇数, 因为奇数加奇
数才是偶数,据此解答。
【详解】新星小学五(2)班有学生 30 名, 总人数是偶数。若第一个社区只能派奇数名同学,
第二个社区派的人数为奇数,因为奇数+奇数=偶数。
答:第二个社区派的人数是奇数,因为奇数+奇数=偶数。
【点睛】本题考查了奇数和偶数的运算性质, 本题关键是根据奇数+奇数=偶数, 奇数+偶
数=奇数来判断。
16 .2 个; 3 个
【分析】每 5 个苹果装成一盘,则苹果的个数是 5 的人倍数,由 5 的倍数的特征:个位是 0
或 5 的数是 5 的倍数可知, 70 和 65 是 5 的倍数由此解答。
【详解】70-68 =2(个)
68-65 =3(个)
答:至少再拿来 2 个或拿走 3 个苹果才能正好装完。
【点睛】本题主要考查 5 的倍数特征的应用, 理解“至少再拿来几个或拿走几个”是解题的关
键。
17 .2 的倍数有: 560 、506 、650
5 的倍数有 560 、650 、605
同时是 2 和 5 的倍数有: 560 、650
18 .32 件
【分析】由于每相邻的两个偶数相差 2,所以三个连续偶数的和是中间偶数的 3 倍, 由此求
出中间偶数,再减去 2 即可。
【详解】 102÷3-2
=34-2
=32(件)
答:笑笑做了 32 件好事。
【点睛】本题主要考查连续偶数的特征,解题时要明确每相邻的两个偶数相差 2。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
