人教版数学八年级下册同步练习16.1.2 二次根式的性质(含答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习16.1.2 二次根式的性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 56.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 08:13:01 | ||
图片预览

文档简介
第十六章二次根式
16.1 二次根式 第2课时 二次根式的性质
1.[2023泰州] 计算等于( )
A.±2 B.2 C.4 D.
2.若等式=()2成立,则实数a的取值范围是( )
A.a>0 B.a<0
C.a≥0 D.a≤0
3.若+=0,则a2 023b2 024的值是( )
A.1 B.-1
C.0 D.1或-1
4.若a<2,化简-3=( )
A.a-5 B.5-a
C.1-a D.-1-a
5.若=1-x,则x的取值范围是( )
A.x≤1 B.x≥1
C.x<1 D.x>1
6.已知三角形的三条边长为3,5,k,化简:|9-k|+=( )
A.8 B.-8
C.2k-10 D.10-2k
7.下列式子中,属于代数式的有 .
①a2+3; ②ab; ③(x≥1);
④(y≠1); ⑤x+y=3.
8.比较与的大小.
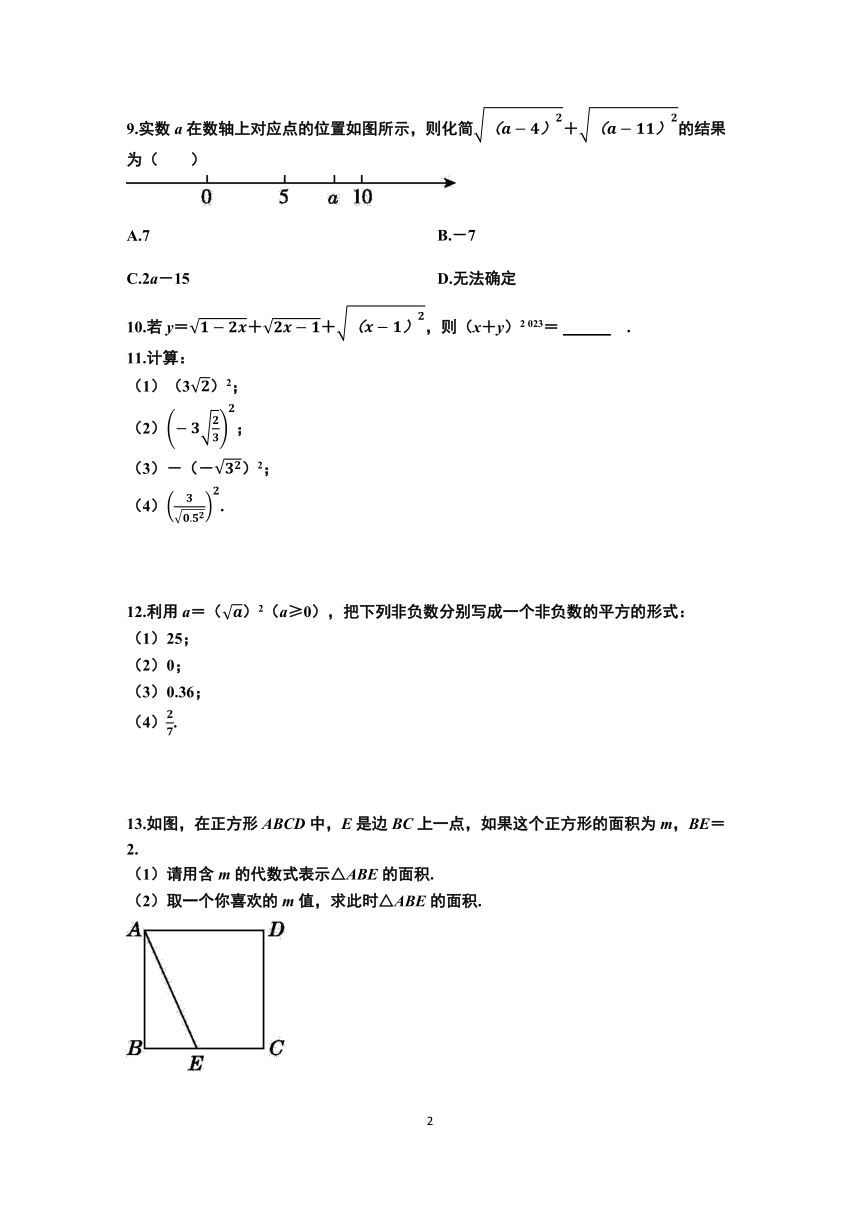
9.实数a在数轴上对应点的位置如图所示,则化简+的结果为( )
A.7 B.-7
C.2a-15 D.无法确定
10.若y=++,则(x+y)2 023= .
11.计算:
(1)(3)2;
(2);
(3)-(-)2;
(4).
12.利用a=()2(a≥0),把下列非负数分别写成一个非负数的平方的形式:
(1)25;
(2)0;
(3)0.36;
(4).
13.如图,在正方形ABCD中,E是边BC上一点,如果这个正方形的面积为m,BE=2.
(1)请用含m的代数式表示△ABE的面积.
(2)取一个你喜欢的m值,求此时△ABE的面积.
14.我们称用基本运算符号把数或表示数的字母连接起来的式子为代数式.前面已经学习了整式、分式和二次根式,当被除数是一个二次根式,除数是一个整式时,求得的商就会出现类似的形式,我们把形如的式子称为根分式,例如,都是根分式.
(1)写出根分式中x的取值范围: ;
(2)小明在解方程-=1时,采用了下面的方法:
去分母,得-=2, ①
∵(-)(+)=()2-()2=(24-x)-(8-x)=16,
∴+=8, ②
由①②可得
将=5两边平方可解得x=-1,经检验:x=-1是原方程的解.
∴原方程的解为x=-1.
请你学习小明的方法,解下面的方程:
①+=1.
②+=1.
15.设m=+(1≤a≤2),求m10+m9+m8+…+m-22的值.
1
参考答案
1.B 2.C 3.B 4.D 5.A 6.A 7.①②③④
8.解:∵==,=,
>,
∴>.
9.A 10.1
11.解:(1)(3)2=9×2=18.
(2)=9×=6.
(3)-(-)2=-9.
(4)==36.
12.解:(1)25=()2=52.
(2)0=()2=02.
(3)0.36=()2=0.62.
(4)=.
13.解:(1)∵正方形的面积为m,∴正方形的边长AB=.又∵BE=2,∴S△ABE=BE·AB=×2×=.
(2)(答案不唯一)当m=4时,△ABE的面积为2.
14.解:(1)x≥0且x≠2
(2)①∵+=1,
∴+=18.
∵(+)(-)=x2+46-x2-10=36,
∴-=2,
∴=10,=8.
将=10两边平方可解得x=±3,
经检验:x=±3是原方程的解.
∴原方程的解为x=±3.
②∵+=1,
∴+=4x.
∵(+)(-)=8x,
∴-=2,
∴=2x+1,=2x-1.
将=2x+1两边平方可解得x=3,
经检验:x=3是原方程的解.
∴原方程的解为x=3.
15.解:∵1≤a≤2,∴0≤a-1≤1,
∴m=+=+1+1-=2.
∴m10+m9+m8+…+m-22=(m10+m9+m8+…+m+1)-23
=-23
=-23
=211-1-23
=2 048-1-23
=2 024.
16.1 二次根式 第2课时 二次根式的性质
1.[2023泰州] 计算等于( )
A.±2 B.2 C.4 D.
2.若等式=()2成立,则实数a的取值范围是( )
A.a>0 B.a<0
C.a≥0 D.a≤0
3.若+=0,则a2 023b2 024的值是( )
A.1 B.-1
C.0 D.1或-1
4.若a<2,化简-3=( )
A.a-5 B.5-a
C.1-a D.-1-a
5.若=1-x,则x的取值范围是( )
A.x≤1 B.x≥1
C.x<1 D.x>1
6.已知三角形的三条边长为3,5,k,化简:|9-k|+=( )
A.8 B.-8
C.2k-10 D.10-2k
7.下列式子中,属于代数式的有 .
①a2+3; ②ab; ③(x≥1);
④(y≠1); ⑤x+y=3.
8.比较与的大小.
9.实数a在数轴上对应点的位置如图所示,则化简+的结果为( )
A.7 B.-7
C.2a-15 D.无法确定
10.若y=++,则(x+y)2 023= .
11.计算:
(1)(3)2;
(2);
(3)-(-)2;
(4).
12.利用a=()2(a≥0),把下列非负数分别写成一个非负数的平方的形式:
(1)25;
(2)0;
(3)0.36;
(4).
13.如图,在正方形ABCD中,E是边BC上一点,如果这个正方形的面积为m,BE=2.
(1)请用含m的代数式表示△ABE的面积.
(2)取一个你喜欢的m值,求此时△ABE的面积.
14.我们称用基本运算符号把数或表示数的字母连接起来的式子为代数式.前面已经学习了整式、分式和二次根式,当被除数是一个二次根式,除数是一个整式时,求得的商就会出现类似的形式,我们把形如的式子称为根分式,例如,都是根分式.
(1)写出根分式中x的取值范围: ;
(2)小明在解方程-=1时,采用了下面的方法:
去分母,得-=2, ①
∵(-)(+)=()2-()2=(24-x)-(8-x)=16,
∴+=8, ②
由①②可得
将=5两边平方可解得x=-1,经检验:x=-1是原方程的解.
∴原方程的解为x=-1.
请你学习小明的方法,解下面的方程:
①+=1.
②+=1.
15.设m=+(1≤a≤2),求m10+m9+m8+…+m-22的值.
1
参考答案
1.B 2.C 3.B 4.D 5.A 6.A 7.①②③④
8.解:∵==,=,
>,
∴>.
9.A 10.1
11.解:(1)(3)2=9×2=18.
(2)=9×=6.
(3)-(-)2=-9.
(4)==36.
12.解:(1)25=()2=52.
(2)0=()2=02.
(3)0.36=()2=0.62.
(4)=.
13.解:(1)∵正方形的面积为m,∴正方形的边长AB=.又∵BE=2,∴S△ABE=BE·AB=×2×=.
(2)(答案不唯一)当m=4时,△ABE的面积为2.
14.解:(1)x≥0且x≠2
(2)①∵+=1,
∴+=18.
∵(+)(-)=x2+46-x2-10=36,
∴-=2,
∴=10,=8.
将=10两边平方可解得x=±3,
经检验:x=±3是原方程的解.
∴原方程的解为x=±3.
②∵+=1,
∴+=4x.
∵(+)(-)=8x,
∴-=2,
∴=2x+1,=2x-1.
将=2x+1两边平方可解得x=3,
经检验:x=3是原方程的解.
∴原方程的解为x=3.
15.解:∵1≤a≤2,∴0≤a-1≤1,
∴m=+=+1+1-=2.
∴m10+m9+m8+…+m-22=(m10+m9+m8+…+m+1)-23
=-23
=-23
=211-1-23
=2 048-1-23
=2 024.
