2023-2024学年北师大版八年级数学下册第一章三角形的证明回顾与思考课件(20张ppt)
文档属性
| 名称 | 2023-2024学年北师大版八年级数学下册第一章三角形的证明回顾与思考课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 651.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-09 08:37:31 | ||
图片预览





文档简介
(共20张PPT)
第一章 三角形的证明
回顾与思考(2)
北师大版八年级数学(下)
学习目标(1分钟)
1、能够综合运用与线段垂直平分线、角平分线的性质定理有关的结论解决问题;
2、会用尺规作线段的垂直平分线、角的平分线;能够用尺规作等腰三角形;
3、反证法的初步理解和运用;了解逆命题、逆定理的概念,会识别两个互逆命题,知道原命题成立其逆命题不一定成立.
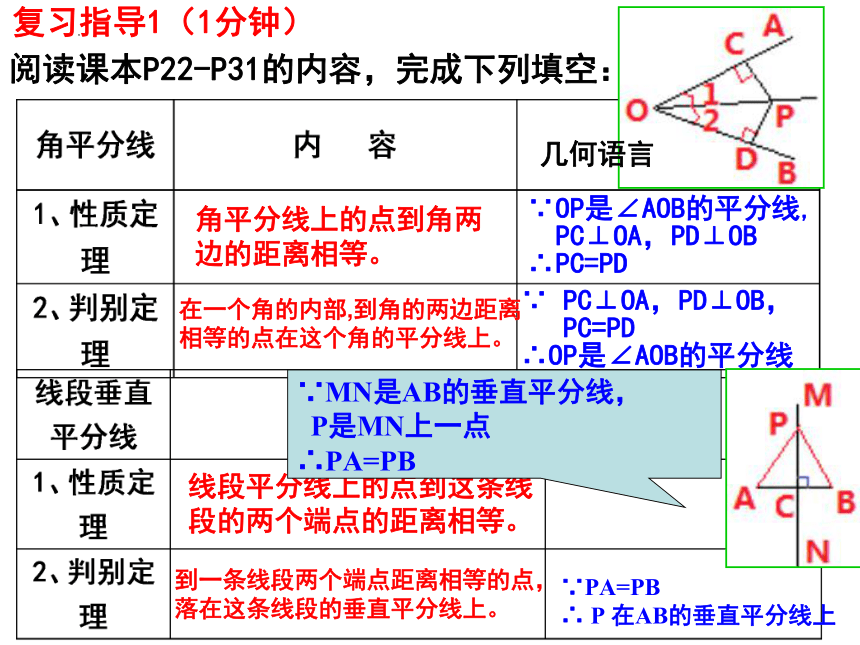
阅读课本P22-P31的内容,完成下列填空:
复习指导1(1分钟)
角平分线上的点到角两边的距离相等。
∵OP是∠AOB的平分线,
PC⊥OA,PD⊥OB
∴PC=PD
∵ PC⊥OA,PD⊥OB,
PC=PD
∴OP是∠AOB的平分线
线段平分线上的点到这条线段的两个端点的距离相等。
在一个角的内部,到角的两边距离相等的点在这个角的平分线上。
到一条线段两个端点距离相等的点,落在这条线段的垂直平分线上。
几何语言
几何语言
∵MN是AB的垂直平分线,
P是MN上一点
∴PA=PB
∵PA=PB
∴ P 在AB的垂直平分线上
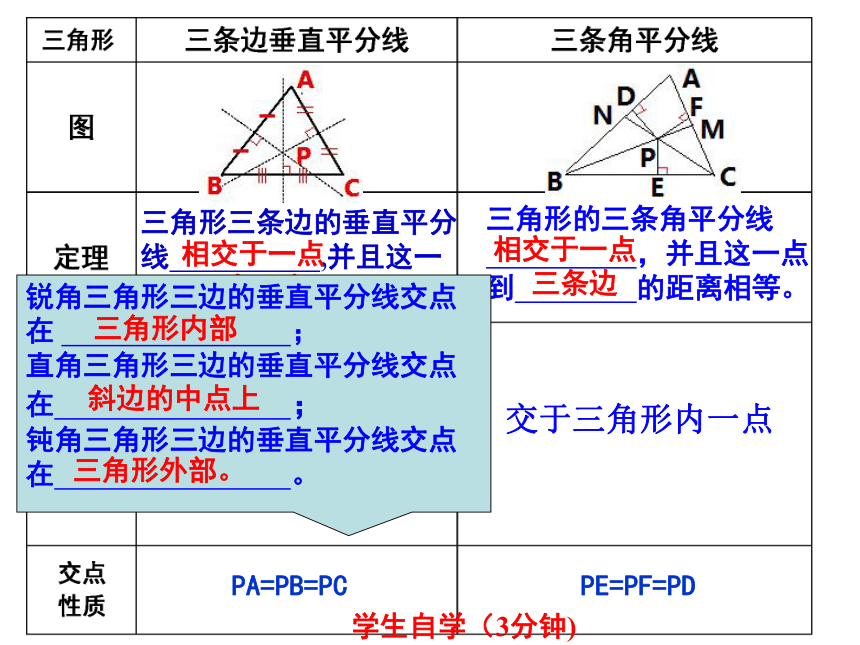
学生自学(3分钟)
三角形的三条角平分线
,并且这一点到 的距离相等。
交于三角形内一点
PE=PF=PD
三角形三条边的垂直平分线 ,并且这一点到 的距离相等.
相交于一点
三个顶点
相交于一点
三条边
锐角三角形三边的垂直平分线交点在 ;
直角三角形三边的垂直平分线交点在 ;
钝角三角形三边的垂直平分线交点在 。
三角形内部
斜边的中点上
三角形外部。
PA=PB=PC
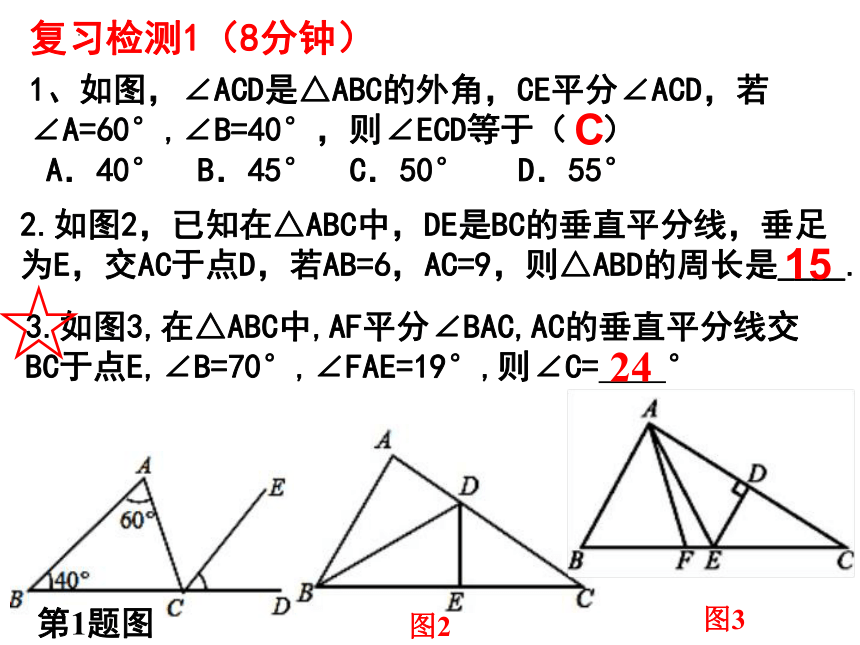
复习检测1(8分钟)
1、如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
C
第1题图
2.如图2,已知在△ABC中,DE是BC的垂直平分线,垂足
为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是____.
15
图2
3.如图3,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= °
24
图3
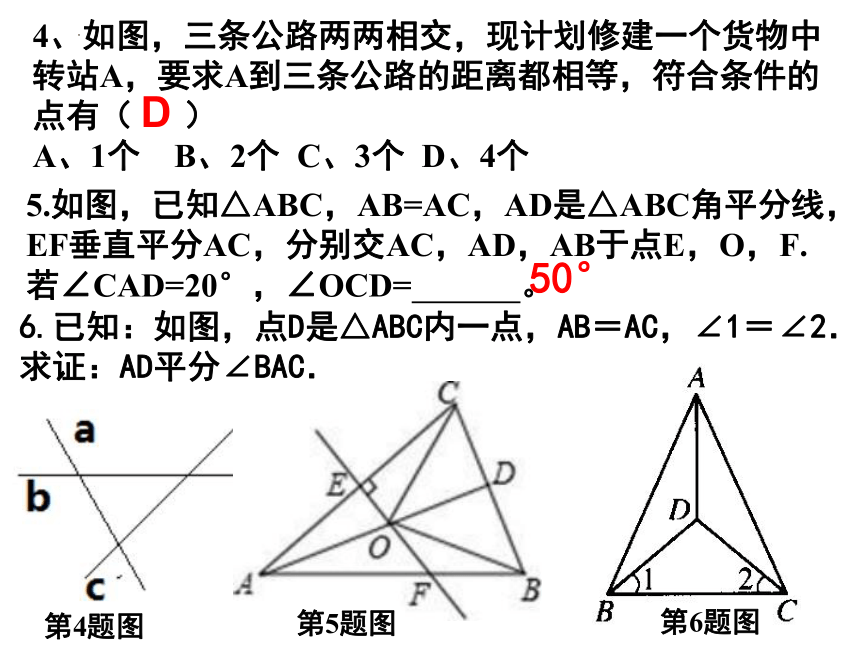
4、如图,三条公路两两相交,现计划修建一个货物中转站A,要求A到三条公路的距离都相等,符合条件的点有( )
A、1个 B、2个 C、3个 D、4个
D
第4题图
5.如图,已知△ABC,AB=AC,AD是△ABC角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,O,F.若∠CAD=20°,∠OCD= 。
第5题图
50°
6.已知:如图,点D是△ABC内一点,AB=AC,∠1=∠2.
求证:AD平分∠BAC.
第6题图
复习指导2(1分钟)
自学教材P2—P20有关内容,思考并回答以下问题:
1.反证法的一般步骤有哪些?
2.如果一个命题的 和 分别是另一个命题的 和 那么这两个命题称为 ,其中一个命题称为另一个命题的 .
条件
结论
结论
条件
互逆命题
逆命题
范例:在△ABC中,AB≠AC,求证:∠B ≠ ∠ C
证明:假设 ,
则 ( )
这与已知条件 矛盾.
∴假设不成立.
∴ .
∠B = ∠ C
AB=AC
等角对等边
AB≠AC
∠B ≠ ∠ C
学生自学,教师巡视(3分钟)
3.如果一个 的逆命题经过证明是真命题,那么它是一个 ,这两个定理称为 ,其中一个定理称另一个定理的 .
4.任何一个命题都有 ,但任何一个定理未必都有 。
定理
定理
互逆定理
逆定理
逆命题
逆定理
学生自学,教师巡视(3分钟)
复习指导2(1分钟)
阅读课本P22-P31的内容,并思考以下问题:
1、如何利用尺规作线段的垂直平分线、角的平分线?如何经过已知一点作已知直线的垂线?
2、尺规作图,要注意什么细节?
(1)作图痕迹要描黑
(2)尺规作图要“下结论”
1.用反证法证明:三角形中最多有一个直角或钝角时,应先假设
2.下列命题的逆命题是假命题的是( )
A.等腰三角形是等边三角形
B.等腰三角形的两个底角相等
C.三边对应相等的两个三角形全等
D.同位角相等
D
三角形中至少有两个直角或钝角
3.下列说法,正确的是( )
A.每个定理都有逆定理B.真命题的逆命题都是真命题C.每个命题都有逆命题D.假命题的逆命题都是假命题
C
复习检测1(3分钟)
图 形
已 知 条 件
结 论
P
C
OC平分∠AOB
PD⊥OA
PE⊥OB
PD=PE
PC
垂直平分
AB
PA=PB
小结(3分钟)
本节课你回顾了那些知识点
易错点:
尺规作线段的垂直平分线或角的平分线时,
要注意: 和
作图痕迹要描黑
下结论
P
C
性质
判定方法
判定方法
性质
PD=PE
PD⊥OA
PE⊥OB
OC平分∠AOB
PA=PB
AC=CB
PC垂直
平分AB
当堂训练(15分钟)
1.如图1,在△ABC中,AB=AC,∠C=70°,MN是AB的垂直平分线,那么∠NBC= .
30°
图1
2.如图2,O是△ABC内一点,且O到三边AB、AC、BC的距离OF=OE=OD,若∠BAC=70°,则∠BOC=( )
A. 110° B. 115° C. 120° D. 125°
图2
3.如图3,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )
A.11, B.8, C.12, D.3
图3
D
C
B
5.如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
(1)作∠ADC的平分线DF,与AE交于点F;
(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
解:(1)如图所示,DF为所求.
5.如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
(1)作∠ADC的平分线DF,与AE交于点F;
(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
第一章 三角形的证明
回顾与思考(2)
北师大版八年级数学(下)
学习目标(1分钟)
1、能够综合运用与线段垂直平分线、角平分线的性质定理有关的结论解决问题;
2、会用尺规作线段的垂直平分线、角的平分线;能够用尺规作等腰三角形;
3、反证法的初步理解和运用;了解逆命题、逆定理的概念,会识别两个互逆命题,知道原命题成立其逆命题不一定成立.
阅读课本P22-P31的内容,完成下列填空:
复习指导1(1分钟)
角平分线上的点到角两边的距离相等。
∵OP是∠AOB的平分线,
PC⊥OA,PD⊥OB
∴PC=PD
∵ PC⊥OA,PD⊥OB,
PC=PD
∴OP是∠AOB的平分线
线段平分线上的点到这条线段的两个端点的距离相等。
在一个角的内部,到角的两边距离相等的点在这个角的平分线上。
到一条线段两个端点距离相等的点,落在这条线段的垂直平分线上。
几何语言
几何语言
∵MN是AB的垂直平分线,
P是MN上一点
∴PA=PB
∵PA=PB
∴ P 在AB的垂直平分线上
学生自学(3分钟)
三角形的三条角平分线
,并且这一点到 的距离相等。
交于三角形内一点
PE=PF=PD
三角形三条边的垂直平分线 ,并且这一点到 的距离相等.
相交于一点
三个顶点
相交于一点
三条边
锐角三角形三边的垂直平分线交点在 ;
直角三角形三边的垂直平分线交点在 ;
钝角三角形三边的垂直平分线交点在 。
三角形内部
斜边的中点上
三角形外部。
PA=PB=PC
复习检测1(8分钟)
1、如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
C
第1题图
2.如图2,已知在△ABC中,DE是BC的垂直平分线,垂足
为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是____.
15
图2
3.如图3,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= °
24
图3
4、如图,三条公路两两相交,现计划修建一个货物中转站A,要求A到三条公路的距离都相等,符合条件的点有( )
A、1个 B、2个 C、3个 D、4个
D
第4题图
5.如图,已知△ABC,AB=AC,AD是△ABC角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,O,F.若∠CAD=20°,∠OCD= 。
第5题图
50°
6.已知:如图,点D是△ABC内一点,AB=AC,∠1=∠2.
求证:AD平分∠BAC.
第6题图
复习指导2(1分钟)
自学教材P2—P20有关内容,思考并回答以下问题:
1.反证法的一般步骤有哪些?
2.如果一个命题的 和 分别是另一个命题的 和 那么这两个命题称为 ,其中一个命题称为另一个命题的 .
条件
结论
结论
条件
互逆命题
逆命题
范例:在△ABC中,AB≠AC,求证:∠B ≠ ∠ C
证明:假设 ,
则 ( )
这与已知条件 矛盾.
∴假设不成立.
∴ .
∠B = ∠ C
AB=AC
等角对等边
AB≠AC
∠B ≠ ∠ C
学生自学,教师巡视(3分钟)
3.如果一个 的逆命题经过证明是真命题,那么它是一个 ,这两个定理称为 ,其中一个定理称另一个定理的 .
4.任何一个命题都有 ,但任何一个定理未必都有 。
定理
定理
互逆定理
逆定理
逆命题
逆定理
学生自学,教师巡视(3分钟)
复习指导2(1分钟)
阅读课本P22-P31的内容,并思考以下问题:
1、如何利用尺规作线段的垂直平分线、角的平分线?如何经过已知一点作已知直线的垂线?
2、尺规作图,要注意什么细节?
(1)作图痕迹要描黑
(2)尺规作图要“下结论”
1.用反证法证明:三角形中最多有一个直角或钝角时,应先假设
2.下列命题的逆命题是假命题的是( )
A.等腰三角形是等边三角形
B.等腰三角形的两个底角相等
C.三边对应相等的两个三角形全等
D.同位角相等
D
三角形中至少有两个直角或钝角
3.下列说法,正确的是( )
A.每个定理都有逆定理B.真命题的逆命题都是真命题C.每个命题都有逆命题D.假命题的逆命题都是假命题
C
复习检测1(3分钟)
图 形
已 知 条 件
结 论
P
C
OC平分∠AOB
PD⊥OA
PE⊥OB
PD=PE
PC
垂直平分
AB
PA=PB
小结(3分钟)
本节课你回顾了那些知识点
易错点:
尺规作线段的垂直平分线或角的平分线时,
要注意: 和
作图痕迹要描黑
下结论
P
C
性质
判定方法
判定方法
性质
PD=PE
PD⊥OA
PE⊥OB
OC平分∠AOB
PA=PB
AC=CB
PC垂直
平分AB
当堂训练(15分钟)
1.如图1,在△ABC中,AB=AC,∠C=70°,MN是AB的垂直平分线,那么∠NBC= .
30°
图1
2.如图2,O是△ABC内一点,且O到三边AB、AC、BC的距离OF=OE=OD,若∠BAC=70°,则∠BOC=( )
A. 110° B. 115° C. 120° D. 125°
图2
3.如图3,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )
A.11, B.8, C.12, D.3
图3
D
C
B
5.如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
(1)作∠ADC的平分线DF,与AE交于点F;
(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
解:(1)如图所示,DF为所求.
5.如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
(1)作∠ADC的平分线DF,与AE交于点F;
(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
