第六章 一次函数--同步练习(广东省佛山市顺德区)
文档属性
| 名称 | 第六章 一次函数--同步练习(广东省佛山市顺德区) |  | |
| 格式 | rar | ||
| 文件大小 | 173.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-13 17:05:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第六章 一次函数
1.函 数 班级:_________姓名:____________
一、选择题
1、下列变量之间的关系中,具有函数关系的有( )
①三角形的面积与底边 ②多边形的内角和与边数
③圆的面积与半径 ④y=中的y与x
A.1个 B.2个 C.3个 D.4个
2、.对于圆的面积公式S=πR2,下列说法中,正确的为( )
A.π是自变量 B.R2是自变量 C.R是自变量 D.πR2是自变量
3、下列函数中,自变量x的取值范围是x≥2的是( )
A.y= B.y= C.y= D.y=·
4、已知函数y=,当x=a时的函数值为1,则a的值为( )
A.3 B.-1 C.-3 D.1
5、某人从A地向B地打长途电话6分钟,按通话时间收费,3分钟内收2.4元,每加一分钟加收1元.则表示电话费y(元)与通话时间x(分)之间的函数关系正确的是( )
二、填空题
6、轮子每分钟旋转60转,则轮子的转数n与时间t(分)之间的关系是__________.其中n t的函数.(填“是”或“不是”)
7、计划花500元购买篮球,所能购买的总数n(个)与单价a(元)的函数关系式为______,其中n a的函数.(填“是”或“不是”).
8、已知矩形的周长为24,设它的一边长为x,那么它的面积y与x之间的函数关系式为______.
9、已知等腰三角形的周长为20 cm,则腰长y(cm)与底边x(cm)的函数关系式为______,其中自变量x的取值范围是______.
三、解答题
10、如图所示堆放钢管.
(1)填表
层数 1 2 3 … x
钢管总数
(2)当堆到x层时,钢管总数如何表示?
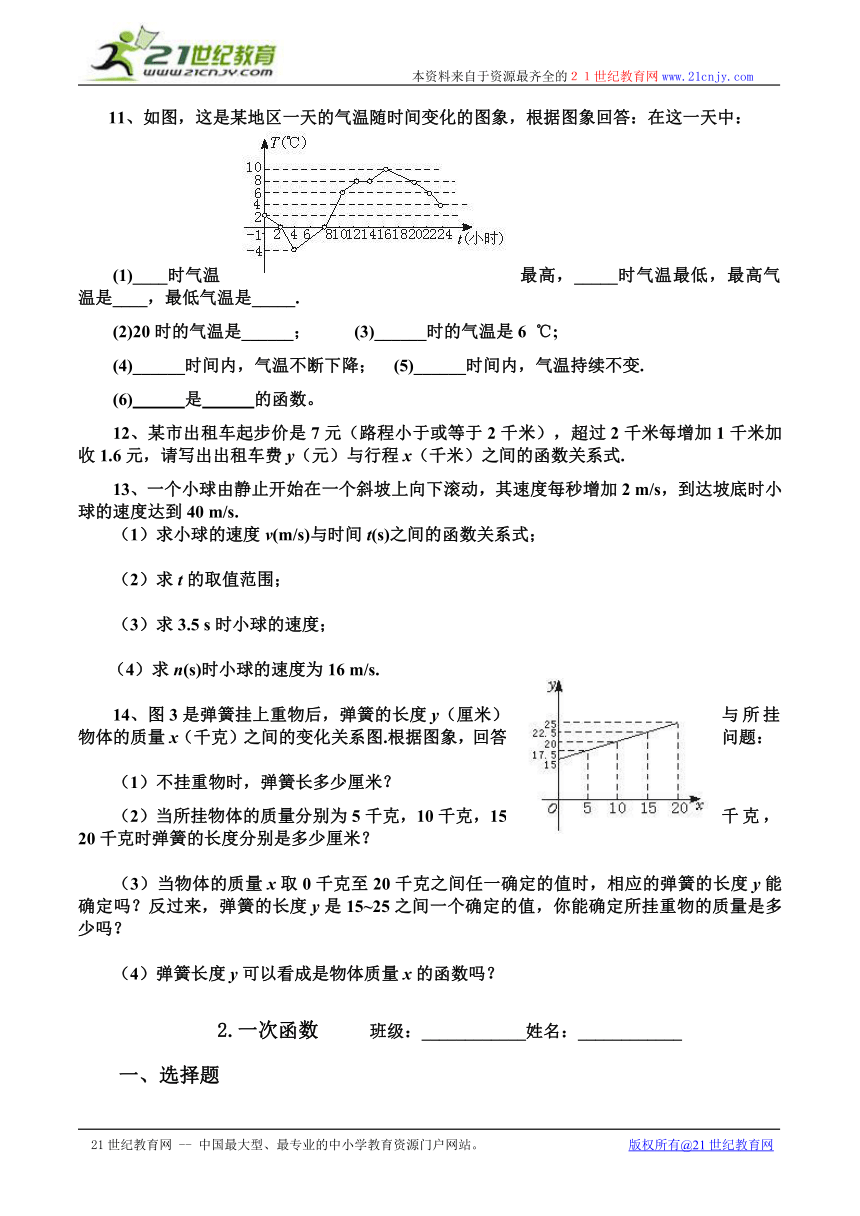
11、如图,这是某地区一天的气温随时间变化的图象,根据图象回答:在这一天中:
(1)____时气温最高,_____时气温最低,最高气温是____,最低气温是_____.
(2)20时的气温是______; (3)______时的气温是6 ℃;
(4)______时间内,气温不断下降; (5)______时间内,气温持续不变.
(6) 是 的函数。
12、某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元,请写出出租车费y(元)与行程x(千米)之间的函数关系式.
13、一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加2 m/s,到达坡底时小球的速度达到40 m/s.
(1)求小球的速度v(m/s)与时间t(s)之间的函数关系式;
(2)求t的取值范围;
(3)求3.5 s时小球的速度;
(4)求n(s)时小球的速度为16 m/s.
14、图3是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:
(1)不挂重物时,弹簧长多少厘米?
(2)当所挂物体的质量分别为5千克,10千克,15千克,20千克时弹簧的长度分别是多少厘米?
(3)当物体的质量x取0千克至20千克之间任一确定的值时,相应的弹簧的长度y能确定吗?反过来,弹簧的长度y是15~25之间一个确定的值,你能确定所挂重物的质量是多少吗?
(4)弹簧长度y可以看成是物体质量x的函数吗?
2.一次函数 班级:____________姓名:____________
一、选择题
1、下列函数中,是一次函数但不是正比例函数的为( )
A、y=- B、y=- C、y=- D、y=
2、下列各关系中,符合正比例关系的是( )
A.正方形的周长P和它的一边长a
B.距离s一定时,速度v和时间t
C.圆的面积S和圆的半径r
D.正方体的体积V和棱长a
3、若y=(m-1)x是正比例函数,则m的值为( )
A、1 B、-1 C、1或-1 D、或-
4、若函数y=(3m-2)x2+(1-2m)x(m为常数)是正比例函数,则m的值为( )
A、m> B、m< C、m= D、m=
5、若5y+2与x-3成正比例,则y是x的( )
A、正比例函数 B、一次函数
C、没有函数关系 D、以上答案均不正确
二、填空题
6、一次函数y=-7x+3中,k=______,b=______.
7、已知y-2=kx(k≠0),且当x=1时,y=7,则y与x之间的关系式为______.
8、某油箱中有油20升,油从管道中均匀流出10分钟可流尽,则油箱中剩油量G(升)与流出时间t(分)之间的函数关系式为______,自变量t的取值范围是______.
9、某种国库券的年利率是2.45%,则存满三年的本息和y与本金x之间的函数关系式为______.
10、某林场现有森林面积为1560平方千米,计划今后每年增加160平方千米的树林,那么森林面积y(平方千米)与年数x的函数关系式为______,6年后林场的森林面积为______.
三、解答题
11、写出一次函数和正比例函数的表达式,并指出它们的区别和联系.
12、等腰三角形的周长为12,底边长为y,腰长为x,求y与x之间的函数关系式,并写出自变量的取值范围.
13、如图,在△ABC中,∠B与∠C的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式,并判断y是不是x的一次函数,指出自变量的取值范围.
14、某商店出售某商品时,在进价的基础上加一定的利润,其数量x与售价y的关系如下表所示.请根据表中所提供的信息,列出y与x的函数关系式并求出当数量是2.5千克时的售价.
数量x(千克) 1 2 3 4 …
售价y(元) 8+0.4 16+0.8 24+1.2 32+1.6 …
15、甲乙两地相距500千米,汽车从甲地以每小时80千米的速度开往乙地.
(1)写出汽车离乙地的距离s(千米)与开出时间t(小时)之间的函数关系式,并指出是不是一次函数;
(2)写出自变量的取值范围;
(3)汽车从甲地开出多久,离乙地为100千米
3.一次函数的图象 班级:___________姓名:_____________
一、选择题
1、函数y=kx的图象经过点P(3,-1),则k的值为( )
A、3 B、-3 C、 D、-
2、下列函数中,图象经过原点的为( )
A、y=5x+1 B、y=-5x-1
C、y=- D、y=
3、若一次函数y=kx+b中,y随x的增大而减小,则( )
A、k<0,b<0 B、k<0,b>0
C、k<0,b≠0 D、k<0,b为任意数
4、当x=5时一次函数y=2x+k和y=3kx-4的值相同,那么k和y的值分别为( )
A、1,11 B、-1,9 C、5,11 D、3,3
5、若直线y=kx+b经过A(1,0),B(0,1),则( )
A、k=-1,b=-1 B、k=1,b=1
C、k=1,b=-1 D、k=-1,b=1
二、填空题
6、把一个函数的自变量x与对应的因变量y的值分别作为点的______和______,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做该函数的______.
7、作函数图象的一般步骤为______,______,______;一次函数的图象是一条______.
8、直线y=3-9x与x轴的交点坐标为______,与y轴的交点坐标为______.
9、一次函数y=5kx-5k-3,当k=______时,图象过原点;当k______时,y随x的增大而增大.
10、在一次函数y=2x-5中,当x由3增大到4时,y的值由______;当x由-3增大到-2时,y的值______.
三、解答题
11、在同一直角坐标系中,画出函数y=x,y=x,y=5x的图象,然后比较哪一个与x轴正方向所成的锐角最大,由此你得到什么猜想?再选几个图象验
证你的猜想.
12、已知直线y=(5-3m)x+m-4与直线y=x+6平行,求此直线的解析式.
13、作出函数y=x-3的图象并回答:
(1)当x的值增加时,y的值如何变化?
(2)当x取何值时,y>0,y=0,y<0.
14、作出函数y=x-4的图象,并求它的图象与x轴、y轴所围成的图形的面积.
15、某单位急需用车,但又不准备买车,他们准备和一个个体车主或一国营出租车公司其中的一家签订月租车合同.设汽车每月行驶x km,应付给个体车主的月费用是y1元,应付给出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题:
(1)每月行驶的路程在什么范围内时,租国营公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300 km,那么这个单位租哪家的车合算?
6.4确定一次函数的表达式
班别: 姓名:
一、填空题
1. 某物体沿一个斜坡下滑,它的速度v(米/秒)与其下滑t(秒)的关系如图所示,则
(1) 下滑2秒时物体的速度为__________________.
(2) V(米/秒)与t(秒)之间的函数关系式为________________.
(3) 下滑3秒时物体的速度为________________.
2. 若一次函数y=x+b的图象过点A(1,-1),则b=__________。
3. 一次函数y=kx+b的图象如图所示,看图填空:
(1)当x=0时,y=____________;当x=____________时,y=0.
(2)k=__________,b=____________.
(3)当x=5时,y=__________;当y=30时,x=___________.
二、解答题:
1. 已知一次函数的图象经过点(2,1)和(-1,-3)
(1) 求此一次函数表达式;
(2) 求此一次函数与x轴、y轴的交点坐标;
(3) 求此一次函数的图象与两坐标轴所围成的三角形的面积。
2. 写出满足下表的一个函数关系式。
3. 根据如图所示的条件,求直线的表达式。
4. 已知直线y=kx+b经过且与坐标轴所围成的三角形的面积为,求该直线的表达式。
5. 一次函数y=k1x-4与正比例函数y=k2x的图象经过点(2,-1),
(1) 分别求出这两个函数的表达式;
(2) 求这两个函数的图象与x轴围成的三角形的面积。
6. 有两条直线和,学生甲解出它们的交点为(3,-2);学生乙因把c抄错而解出它们的交点为试写出这两条直线的表达式。
7. 已知直线与直线y=2x+1的交点的横坐标为2,与直线y=-x-8的交点的纵坐标为-7,求直线的表达式。
5.一次函数图象的应用 班别: 姓名:
一、选择题
1、在函数y=x-1的图象上的点是( )
A、(-3,-2) B、(-4,-3) C、(,) D、(5,)
2、如果一个正比例函数的图象经过点A(3,-1),那么这个正比例函数的解析式为( )
A、y=3x B、y=-3x C、y=x D、y=-x
3、函数y=3x-6和y=-x+4的图象交于一点,这一点的坐标是( )
A、(-,-) B、(,)
C、(,) D、(-2,3)
4、已知直线y=-x+6和y=x-2,则它们与y轴所围成的三角形的面积为( )
A、6 B、10 C、20 D、12
5、直线y=kx+b的图象如图所示,则( )
A、k=-,b=-2 B、k=,b=-2
C、k=-,b=-2 D、k=,b=-2
二、填空题
6、函数y=5x-10,当x=2时,y=______;当x=0时,y=______.
7、函数y=mx-(m-2)的图象经过点(0,3),则m=______.
8、点(1,m),(2,n)在函数y=-x+1的图象上,则m、n的大小关系是______.
9、当b=______时,直线y=x+b与直线y=2x+3的交点在y轴上.
10、一次函数的图象经过点A(-2,1)和点B(1,-1),它的解析式是______.
三、解答题
11、已知一次函数y=(m-3)x+2m+4的图象过直线y=-x+4与y轴的交点M,求此一次函数的解析式.
12、已知一次函数y=2x+b与坐标轴围成的三角形面积是4,求b的值.
13、某地长途客运公司规定,旅客可随身携带一定质量的行李.如果超过规定,则需购买行李票,行李票费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.
(1)写出y与x之间的函数关系式,并指出自变量x的取值范围.
(2)旅客最多可免费携带多少千克行李?
14、直线y=kx+b过点A(-1,5)且平行于直线y=-x.
(1)求这条直线的解析式.
(2)点B(m,-5)在这条直线上,O为坐标原点,求m的值及△AOB的面积.
15、甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供了两个方面的信息,如甲乙两图.甲调查表明:每个甲鱼池平均生产量从第一年1万只甲鱼上升到第6年的2万只;乙调查表明:甲鱼池由第一年30个减少到第6年的10个.请你根据提供的信息说明:
(1)第2年甲鱼池的个数及全县出产甲鱼总数;
(2)到第6年这个县的甲鱼养殖业的规模比第一年是扩大了还是缩小了?说明理由.
(3)哪一年的规模最大?说明理由.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第六章 一次函数
1.函 数 班级:_________姓名:____________
一、选择题
1、下列变量之间的关系中,具有函数关系的有( )
①三角形的面积与底边 ②多边形的内角和与边数
③圆的面积与半径 ④y=中的y与x
A.1个 B.2个 C.3个 D.4个
2、.对于圆的面积公式S=πR2,下列说法中,正确的为( )
A.π是自变量 B.R2是自变量 C.R是自变量 D.πR2是自变量
3、下列函数中,自变量x的取值范围是x≥2的是( )
A.y= B.y= C.y= D.y=·
4、已知函数y=,当x=a时的函数值为1,则a的值为( )
A.3 B.-1 C.-3 D.1
5、某人从A地向B地打长途电话6分钟,按通话时间收费,3分钟内收2.4元,每加一分钟加收1元.则表示电话费y(元)与通话时间x(分)之间的函数关系正确的是( )
二、填空题
6、轮子每分钟旋转60转,则轮子的转数n与时间t(分)之间的关系是__________.其中n t的函数.(填“是”或“不是”)
7、计划花500元购买篮球,所能购买的总数n(个)与单价a(元)的函数关系式为______,其中n a的函数.(填“是”或“不是”).
8、已知矩形的周长为24,设它的一边长为x,那么它的面积y与x之间的函数关系式为______.
9、已知等腰三角形的周长为20 cm,则腰长y(cm)与底边x(cm)的函数关系式为______,其中自变量x的取值范围是______.
三、解答题
10、如图所示堆放钢管.
(1)填表
层数 1 2 3 … x
钢管总数
(2)当堆到x层时,钢管总数如何表示?
11、如图,这是某地区一天的气温随时间变化的图象,根据图象回答:在这一天中:
(1)____时气温最高,_____时气温最低,最高气温是____,最低气温是_____.
(2)20时的气温是______; (3)______时的气温是6 ℃;
(4)______时间内,气温不断下降; (5)______时间内,气温持续不变.
(6) 是 的函数。
12、某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元,请写出出租车费y(元)与行程x(千米)之间的函数关系式.
13、一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加2 m/s,到达坡底时小球的速度达到40 m/s.
(1)求小球的速度v(m/s)与时间t(s)之间的函数关系式;
(2)求t的取值范围;
(3)求3.5 s时小球的速度;
(4)求n(s)时小球的速度为16 m/s.
14、图3是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:
(1)不挂重物时,弹簧长多少厘米?
(2)当所挂物体的质量分别为5千克,10千克,15千克,20千克时弹簧的长度分别是多少厘米?
(3)当物体的质量x取0千克至20千克之间任一确定的值时,相应的弹簧的长度y能确定吗?反过来,弹簧的长度y是15~25之间一个确定的值,你能确定所挂重物的质量是多少吗?
(4)弹簧长度y可以看成是物体质量x的函数吗?
2.一次函数 班级:____________姓名:____________
一、选择题
1、下列函数中,是一次函数但不是正比例函数的为( )
A、y=- B、y=- C、y=- D、y=
2、下列各关系中,符合正比例关系的是( )
A.正方形的周长P和它的一边长a
B.距离s一定时,速度v和时间t
C.圆的面积S和圆的半径r
D.正方体的体积V和棱长a
3、若y=(m-1)x是正比例函数,则m的值为( )
A、1 B、-1 C、1或-1 D、或-
4、若函数y=(3m-2)x2+(1-2m)x(m为常数)是正比例函数,则m的值为( )
A、m> B、m< C、m= D、m=
5、若5y+2与x-3成正比例,则y是x的( )
A、正比例函数 B、一次函数
C、没有函数关系 D、以上答案均不正确
二、填空题
6、一次函数y=-7x+3中,k=______,b=______.
7、已知y-2=kx(k≠0),且当x=1时,y=7,则y与x之间的关系式为______.
8、某油箱中有油20升,油从管道中均匀流出10分钟可流尽,则油箱中剩油量G(升)与流出时间t(分)之间的函数关系式为______,自变量t的取值范围是______.
9、某种国库券的年利率是2.45%,则存满三年的本息和y与本金x之间的函数关系式为______.
10、某林场现有森林面积为1560平方千米,计划今后每年增加160平方千米的树林,那么森林面积y(平方千米)与年数x的函数关系式为______,6年后林场的森林面积为______.
三、解答题
11、写出一次函数和正比例函数的表达式,并指出它们的区别和联系.
12、等腰三角形的周长为12,底边长为y,腰长为x,求y与x之间的函数关系式,并写出自变量的取值范围.
13、如图,在△ABC中,∠B与∠C的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式,并判断y是不是x的一次函数,指出自变量的取值范围.
14、某商店出售某商品时,在进价的基础上加一定的利润,其数量x与售价y的关系如下表所示.请根据表中所提供的信息,列出y与x的函数关系式并求出当数量是2.5千克时的售价.
数量x(千克) 1 2 3 4 …
售价y(元) 8+0.4 16+0.8 24+1.2 32+1.6 …
15、甲乙两地相距500千米,汽车从甲地以每小时80千米的速度开往乙地.
(1)写出汽车离乙地的距离s(千米)与开出时间t(小时)之间的函数关系式,并指出是不是一次函数;
(2)写出自变量的取值范围;
(3)汽车从甲地开出多久,离乙地为100千米
3.一次函数的图象 班级:___________姓名:_____________
一、选择题
1、函数y=kx的图象经过点P(3,-1),则k的值为( )
A、3 B、-3 C、 D、-
2、下列函数中,图象经过原点的为( )
A、y=5x+1 B、y=-5x-1
C、y=- D、y=
3、若一次函数y=kx+b中,y随x的增大而减小,则( )
A、k<0,b<0 B、k<0,b>0
C、k<0,b≠0 D、k<0,b为任意数
4、当x=5时一次函数y=2x+k和y=3kx-4的值相同,那么k和y的值分别为( )
A、1,11 B、-1,9 C、5,11 D、3,3
5、若直线y=kx+b经过A(1,0),B(0,1),则( )
A、k=-1,b=-1 B、k=1,b=1
C、k=1,b=-1 D、k=-1,b=1
二、填空题
6、把一个函数的自变量x与对应的因变量y的值分别作为点的______和______,在直角坐标系中描出它的对应点,所有这些点组成的图形叫做该函数的______.
7、作函数图象的一般步骤为______,______,______;一次函数的图象是一条______.
8、直线y=3-9x与x轴的交点坐标为______,与y轴的交点坐标为______.
9、一次函数y=5kx-5k-3,当k=______时,图象过原点;当k______时,y随x的增大而增大.
10、在一次函数y=2x-5中,当x由3增大到4时,y的值由______;当x由-3增大到-2时,y的值______.
三、解答题
11、在同一直角坐标系中,画出函数y=x,y=x,y=5x的图象,然后比较哪一个与x轴正方向所成的锐角最大,由此你得到什么猜想?再选几个图象验
证你的猜想.
12、已知直线y=(5-3m)x+m-4与直线y=x+6平行,求此直线的解析式.
13、作出函数y=x-3的图象并回答:
(1)当x的值增加时,y的值如何变化?
(2)当x取何值时,y>0,y=0,y<0.
14、作出函数y=x-4的图象,并求它的图象与x轴、y轴所围成的图形的面积.
15、某单位急需用车,但又不准备买车,他们准备和一个个体车主或一国营出租车公司其中的一家签订月租车合同.设汽车每月行驶x km,应付给个体车主的月费用是y1元,应付给出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题:
(1)每月行驶的路程在什么范围内时,租国营公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300 km,那么这个单位租哪家的车合算?
6.4确定一次函数的表达式
班别: 姓名:
一、填空题
1. 某物体沿一个斜坡下滑,它的速度v(米/秒)与其下滑t(秒)的关系如图所示,则
(1) 下滑2秒时物体的速度为__________________.
(2) V(米/秒)与t(秒)之间的函数关系式为________________.
(3) 下滑3秒时物体的速度为________________.
2. 若一次函数y=x+b的图象过点A(1,-1),则b=__________。
3. 一次函数y=kx+b的图象如图所示,看图填空:
(1)当x=0时,y=____________;当x=____________时,y=0.
(2)k=__________,b=____________.
(3)当x=5时,y=__________;当y=30时,x=___________.
二、解答题:
1. 已知一次函数的图象经过点(2,1)和(-1,-3)
(1) 求此一次函数表达式;
(2) 求此一次函数与x轴、y轴的交点坐标;
(3) 求此一次函数的图象与两坐标轴所围成的三角形的面积。
2. 写出满足下表的一个函数关系式。
3. 根据如图所示的条件,求直线的表达式。
4. 已知直线y=kx+b经过且与坐标轴所围成的三角形的面积为,求该直线的表达式。
5. 一次函数y=k1x-4与正比例函数y=k2x的图象经过点(2,-1),
(1) 分别求出这两个函数的表达式;
(2) 求这两个函数的图象与x轴围成的三角形的面积。
6. 有两条直线和,学生甲解出它们的交点为(3,-2);学生乙因把c抄错而解出它们的交点为试写出这两条直线的表达式。
7. 已知直线与直线y=2x+1的交点的横坐标为2,与直线y=-x-8的交点的纵坐标为-7,求直线的表达式。
5.一次函数图象的应用 班别: 姓名:
一、选择题
1、在函数y=x-1的图象上的点是( )
A、(-3,-2) B、(-4,-3) C、(,) D、(5,)
2、如果一个正比例函数的图象经过点A(3,-1),那么这个正比例函数的解析式为( )
A、y=3x B、y=-3x C、y=x D、y=-x
3、函数y=3x-6和y=-x+4的图象交于一点,这一点的坐标是( )
A、(-,-) B、(,)
C、(,) D、(-2,3)
4、已知直线y=-x+6和y=x-2,则它们与y轴所围成的三角形的面积为( )
A、6 B、10 C、20 D、12
5、直线y=kx+b的图象如图所示,则( )
A、k=-,b=-2 B、k=,b=-2
C、k=-,b=-2 D、k=,b=-2
二、填空题
6、函数y=5x-10,当x=2时,y=______;当x=0时,y=______.
7、函数y=mx-(m-2)的图象经过点(0,3),则m=______.
8、点(1,m),(2,n)在函数y=-x+1的图象上,则m、n的大小关系是______.
9、当b=______时,直线y=x+b与直线y=2x+3的交点在y轴上.
10、一次函数的图象经过点A(-2,1)和点B(1,-1),它的解析式是______.
三、解答题
11、已知一次函数y=(m-3)x+2m+4的图象过直线y=-x+4与y轴的交点M,求此一次函数的解析式.
12、已知一次函数y=2x+b与坐标轴围成的三角形面积是4,求b的值.
13、某地长途客运公司规定,旅客可随身携带一定质量的行李.如果超过规定,则需购买行李票,行李票费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.
(1)写出y与x之间的函数关系式,并指出自变量x的取值范围.
(2)旅客最多可免费携带多少千克行李?
14、直线y=kx+b过点A(-1,5)且平行于直线y=-x.
(1)求这条直线的解析式.
(2)点B(m,-5)在这条直线上,O为坐标原点,求m的值及△AOB的面积.
15、甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供了两个方面的信息,如甲乙两图.甲调查表明:每个甲鱼池平均生产量从第一年1万只甲鱼上升到第6年的2万只;乙调查表明:甲鱼池由第一年30个减少到第6年的10个.请你根据提供的信息说明:
(1)第2年甲鱼池的个数及全县出产甲鱼总数;
(2)到第6年这个县的甲鱼养殖业的规模比第一年是扩大了还是缩小了?说明理由.
(3)哪一年的规模最大?说明理由.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
