5.2 运动的合成与分解——小船渡河与关联速度 课件 (共21张PPT) 高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 5.2 运动的合成与分解——小船渡河与关联速度 课件 (共21张PPT) 高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-08 10:58:35 | ||
图片预览






文档简介
(共21张PPT)
运动的合成与分解
小船渡河模型
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
新课引入
小船渡河模型
解决小船过河问题时,要先弄清楚合运动和分运动,小船过河时实际上参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船在静水中的运动(运动方向为船头朝向的方向),船的实际运动(相对于河岸的运动)是合运动。
由于河的宽度是确定的,所以首先应确定渡河的速度,然后计算渡河的时间,再根据等时性分别研究两个分运动或合运动。
新课讲解
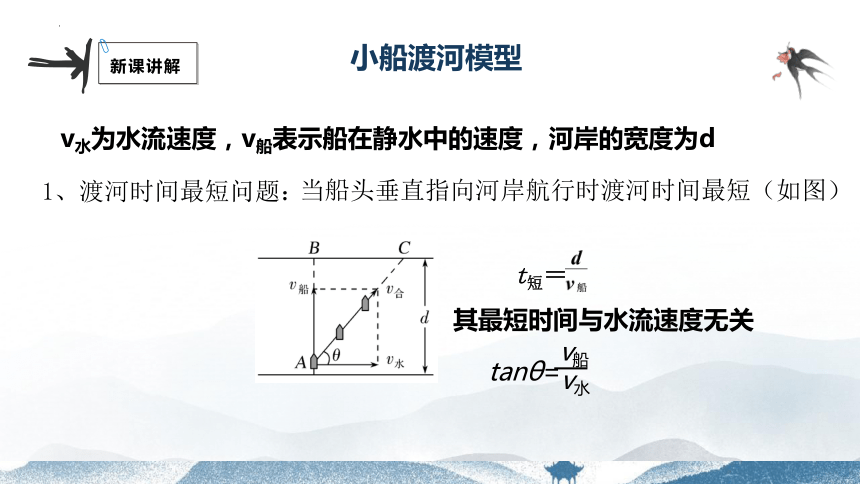
v水为水流速度,v船表示船在静水中的速度,河岸的宽度为d
小船渡河模型
新课讲解
1、渡河时间最短问题:
t短=
当船头垂直指向河岸航行时渡河时间最短(如图)
tanθ=
v水
v船
其最短时间与水流速度无关
(1)当v水小船渡河模型
新课讲解
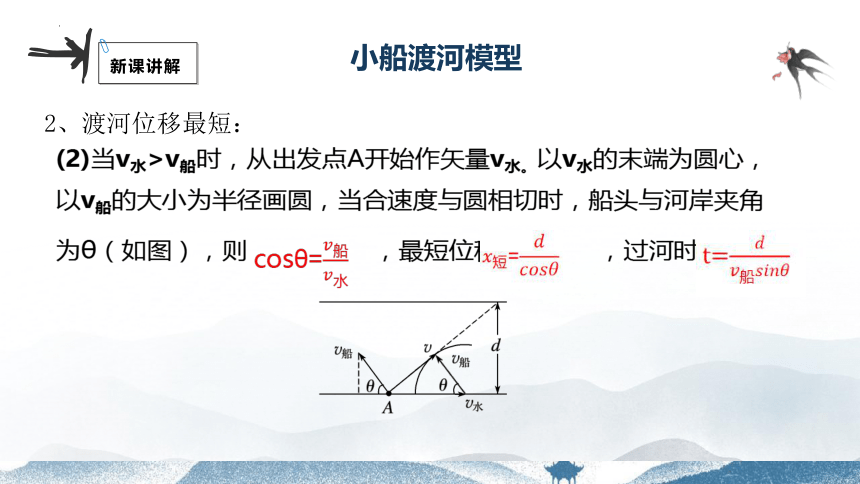
2、渡河位移最短:
cosθ=
(2)当v水>v船时,从出发点A开始作矢量v水。以v水的末端为圆心,以v船的大小为半径画圆,当合速度与圆相切时,船头与河岸夹角为θ(如图),则 ,最短位移
小船渡河模型
新课讲解
2、渡河位移最短:
cosθ=
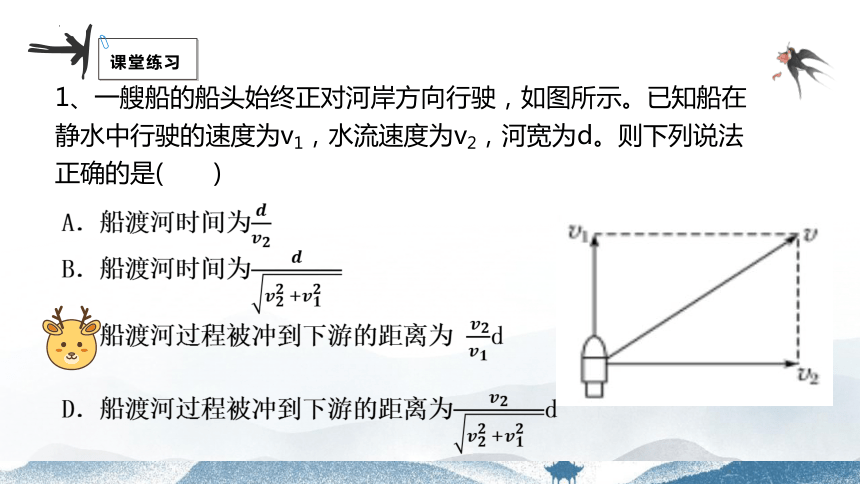
1、一艘船的船头始终正对河岸方向行驶,如图所示。已知船在静水中行驶的速度为v1,水流速度为v2,河宽为d。则下列说法正确的是( )
A.船渡河时间为
B.船渡河时间为
C.船渡河过程被冲到下游的距离为 d
D.船渡河过程被冲到下游的距离为d
课堂练习
2.小明同学遥控小船做过河实验,并绘制了四幅小船过河的航线图如图所示。图中实线为河岸,河水的流动速度不变,方向如图水平向右,虚线为小船从河岸M驶向对岸N的实际航线,小船相对于静水的速度不变。则( )
A
课堂练习
B
C
D
3.一小船在静水中的速度为3 m/s,它在一条河宽为150 m,水流速度为4 m/s的河流中渡河,则该小船( )
A.能到达正对岸
B.渡河的时间可能少于50 s
C.以最短时间渡河时,它沿水流方向的位移大小为200 m
D.以最短位移渡河时,位移大小为150 m
课堂练习
4.(多选)河水的流速与某河岸的距离的变化关系如图甲所示,船在静水中的速度与时间的关系如图乙所示.若要使船以最短时间渡河,下列说法正确的是( )
A.船渡河的最短时间为100 s
B.船在行驶过程中,船头始终与河岸垂直
C.船在河中航行的轨迹是一条直线
D.船在河水中的最大速度为7 m/s
课堂练习
5、小船要渡过100 m宽的河,水流速度为3 m/s,船在静水中的速度为4 m/s,求:
(1)小船渡河的最短时间为多少?位移有多大
(2)欲使船以最小位移渡河,渡河所有时间是多少?
(4)若水流速度是5 m/s,船在静水中的速度保持是4 m/s不变,船能否垂直渡河?
课堂练习
小船渡河模型
两类常见问题:
1、渡河时间最短
船头垂直于河岸航行即可
2、渡河位移最短
①v船 > v水,船能垂直过河,位移最短
②v水>v船,过河位移最短须满足v船 ⊥ v合
课堂小结
1.模型特点
沿绳(杆)方向的速度分量大小相等。
2.思路与方法
合速度→物体的实际运动速度v
方法:v∥与v⊥的合成遵循平行四边形定则。
3.解题原则:根据沿绳(杆)方向的分速度大小相等求解。
分速度→
其一:沿绳(杆)的速度v∥
其二:与绳(杆)垂直的速度v⊥
考点二:关联速度模型
新课讲解
4.解题四步:
①找物体的实际运动方向,即合速度;
②沿绳(杆)方向和垂直于绳(杆)的方向画分速度;
③作平行四边形(矩形);
④找出绳(杆)方向的分速度与和速度的关系式。
新课讲解
沿绳(杆)方向的速度分量大小相等。
1、如图所示,AB杆和墙的夹角为θ 时,杆的A端沿墙下滑的速度大小为v1,B端沿地面的速度大小为v2,则v1、v2的关系是( )
A.v1=v2
B.v1=v2cos θ
C.v1=v2tan θ
D.v1=v2sin θ
课堂练习
2、图中套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大,故在释放B后,A将沿杆上升,当A环上升至与定滑轮的连线处于水平位置时,其上升速度v1≠0,若这时B的速度为v2,则 ( )
A.v2=v1 B.v2>v1
C.v2≠0 D.v2=0
课堂练习
课堂练习
3、如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度v匀速向右运动到如图所示位置时,物体P的速度为( )
A.v B.vcosθ
C. D.
课堂练习
4、(多选)如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为Ff,当轻绳与水面的夹角为θ时,船的速度为v,人的拉力大小为F,则此时( )
A.人拉绳行走的速度为vcosθ
C.船的加速度为
D.船的加速度为
B.人拉绳行走的速度为
课堂练习
6、如图所示,水面上方高度为20 m处有一光滑轻质定滑轮,用绳系住一只船,船离岸的水平距离为 m,岸上的人用3 m/s的恒定速度水平拉绳子,求:
(1)开始时船的速度大小;
(2)5 s末船的速度大小.
(1) m/s (2)5m/s
课堂练习
学海无涯苦作舟
运动的合成与分解
小船渡河模型
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏向上游或下游?为什么?
新课引入
小船渡河模型
解决小船过河问题时,要先弄清楚合运动和分运动,小船过河时实际上参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船在静水中的运动(运动方向为船头朝向的方向),船的实际运动(相对于河岸的运动)是合运动。
由于河的宽度是确定的,所以首先应确定渡河的速度,然后计算渡河的时间,再根据等时性分别研究两个分运动或合运动。
新课讲解
v水为水流速度,v船表示船在静水中的速度,河岸的宽度为d
小船渡河模型
新课讲解
1、渡河时间最短问题:
t短=
当船头垂直指向河岸航行时渡河时间最短(如图)
tanθ=
v水
v船
其最短时间与水流速度无关
(1)当v水
新课讲解
2、渡河位移最短:
cosθ=
(2)当v水>v船时,从出发点A开始作矢量v水。以v水的末端为圆心,以v船的大小为半径画圆,当合速度与圆相切时,船头与河岸夹角为θ(如图),则 ,最短位移
小船渡河模型
新课讲解
2、渡河位移最短:
cosθ=
1、一艘船的船头始终正对河岸方向行驶,如图所示。已知船在静水中行驶的速度为v1,水流速度为v2,河宽为d。则下列说法正确的是( )
A.船渡河时间为
B.船渡河时间为
C.船渡河过程被冲到下游的距离为 d
D.船渡河过程被冲到下游的距离为d
课堂练习
2.小明同学遥控小船做过河实验,并绘制了四幅小船过河的航线图如图所示。图中实线为河岸,河水的流动速度不变,方向如图水平向右,虚线为小船从河岸M驶向对岸N的实际航线,小船相对于静水的速度不变。则( )
A
课堂练习
B
C
D
3.一小船在静水中的速度为3 m/s,它在一条河宽为150 m,水流速度为4 m/s的河流中渡河,则该小船( )
A.能到达正对岸
B.渡河的时间可能少于50 s
C.以最短时间渡河时,它沿水流方向的位移大小为200 m
D.以最短位移渡河时,位移大小为150 m
课堂练习
4.(多选)河水的流速与某河岸的距离的变化关系如图甲所示,船在静水中的速度与时间的关系如图乙所示.若要使船以最短时间渡河,下列说法正确的是( )
A.船渡河的最短时间为100 s
B.船在行驶过程中,船头始终与河岸垂直
C.船在河中航行的轨迹是一条直线
D.船在河水中的最大速度为7 m/s
课堂练习
5、小船要渡过100 m宽的河,水流速度为3 m/s,船在静水中的速度为4 m/s,求:
(1)小船渡河的最短时间为多少?位移有多大
(2)欲使船以最小位移渡河,渡河所有时间是多少?
(4)若水流速度是5 m/s,船在静水中的速度保持是4 m/s不变,船能否垂直渡河?
课堂练习
小船渡河模型
两类常见问题:
1、渡河时间最短
船头垂直于河岸航行即可
2、渡河位移最短
①v船 > v水,船能垂直过河,位移最短
②v水>v船,过河位移最短须满足v船 ⊥ v合
课堂小结
1.模型特点
沿绳(杆)方向的速度分量大小相等。
2.思路与方法
合速度→物体的实际运动速度v
方法:v∥与v⊥的合成遵循平行四边形定则。
3.解题原则:根据沿绳(杆)方向的分速度大小相等求解。
分速度→
其一:沿绳(杆)的速度v∥
其二:与绳(杆)垂直的速度v⊥
考点二:关联速度模型
新课讲解
4.解题四步:
①找物体的实际运动方向,即合速度;
②沿绳(杆)方向和垂直于绳(杆)的方向画分速度;
③作平行四边形(矩形);
④找出绳(杆)方向的分速度与和速度的关系式。
新课讲解
沿绳(杆)方向的速度分量大小相等。
1、如图所示,AB杆和墙的夹角为θ 时,杆的A端沿墙下滑的速度大小为v1,B端沿地面的速度大小为v2,则v1、v2的关系是( )
A.v1=v2
B.v1=v2cos θ
C.v1=v2tan θ
D.v1=v2sin θ
课堂练习
2、图中套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大,故在释放B后,A将沿杆上升,当A环上升至与定滑轮的连线处于水平位置时,其上升速度v1≠0,若这时B的速度为v2,则 ( )
A.v2=v1 B.v2>v1
C.v2≠0 D.v2=0
课堂练习
课堂练习
3、如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度v匀速向右运动到如图所示位置时,物体P的速度为( )
A.v B.vcosθ
C. D.
课堂练习
4、(多选)如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为Ff,当轻绳与水面的夹角为θ时,船的速度为v,人的拉力大小为F,则此时( )
A.人拉绳行走的速度为vcosθ
C.船的加速度为
D.船的加速度为
B.人拉绳行走的速度为
课堂练习
6、如图所示,水面上方高度为20 m处有一光滑轻质定滑轮,用绳系住一只船,船离岸的水平距离为 m,岸上的人用3 m/s的恒定速度水平拉绳子,求:
(1)开始时船的速度大小;
(2)5 s末船的速度大小.
(1) m/s (2)5m/s
课堂练习
学海无涯苦作舟
