第19章 矩形、菱形与正方形单元测试卷
文档属性
| 名称 | 第19章 矩形、菱形与正方形单元测试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 260.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-06 07:02:27 | ||
图片预览



文档简介
第19章 《矩形、菱形与正方形》单元测试卷
一、单选题 ?(每题3分,共8题24分)21世纪教育网版权所
1. 平行四边形、矩形、菱形、正方形都具有的是(??)
A.对角线互相平分
B.对角线互相垂直21世纪教育网版权所
C.对角线相等
D.对角线互相垂直且相等
2. 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是() A.矩形?????? B.菱形?????? C.正方形?????? D.梯形
第2 题图 第4题图
3. 若菱形两条对角线的长分别为10cm和24cm,则这个菱形的周长为(???)
A.13cm
B.26cm
C.34cm
D.52cm
4. 用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是 (?)
A.一组邻边相等的四边形是菱形
B.四边相等的四边形是菱形21世纪教育网版权所
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
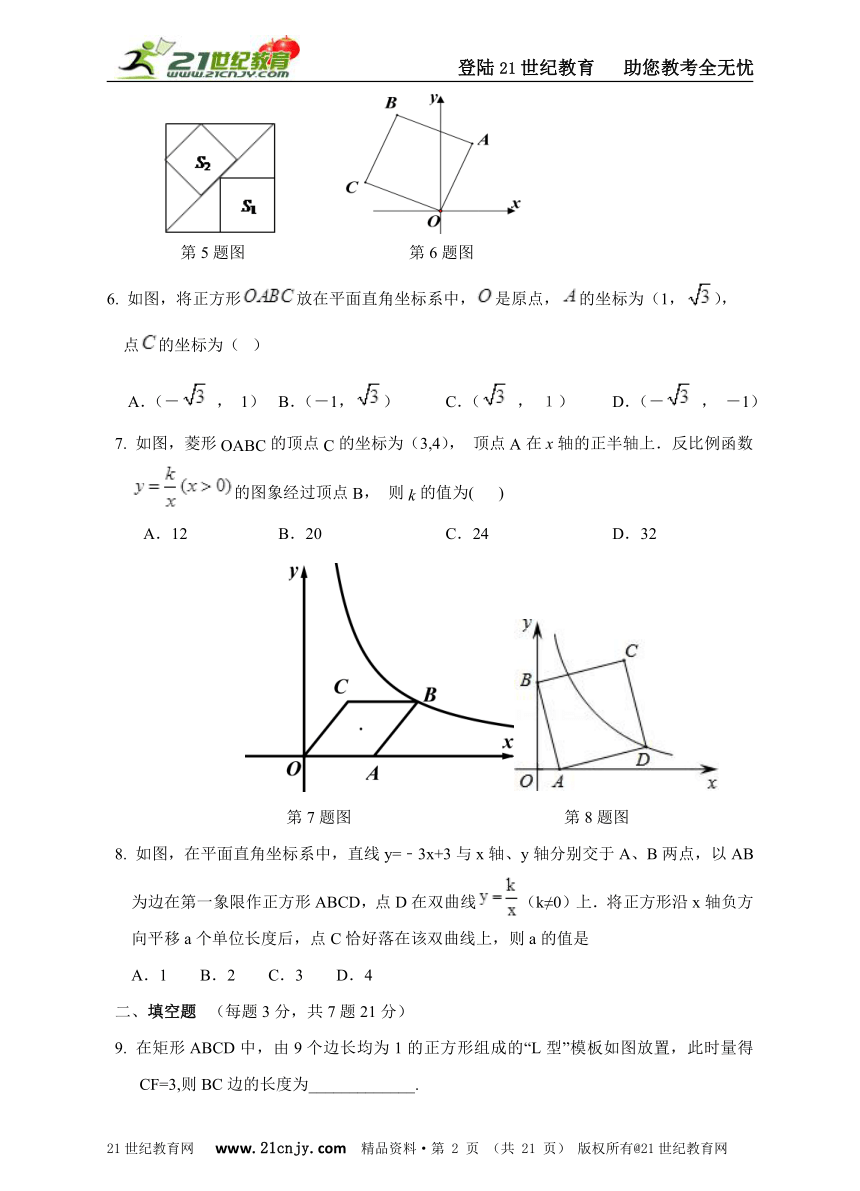
5. 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为 , 则的值为
A.16
B.17
C.18
D.19
第5题图 第6题图
6. 如图,将正方形放在平面直角坐标系中,是原点,的坐标为(1,),
点的坐标为(???)
A.(- , 1)
B.(-1,)
C.( , 1)
D.(- , -1)
7. 如图,菱形OABC的顶点C的坐标为(3,4), 顶点A在x轴的正半轴上.反比例函数
的图象经过顶点B, 则k的值为( ????)?21世纪教育网版权所
A.12
B.20
C.24
D.32
第7题图 第8题图
8. 如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是 A.1?????? B.2?????? C.3?????? D.4
二、填空题 ?(每题3分,共7题21分)
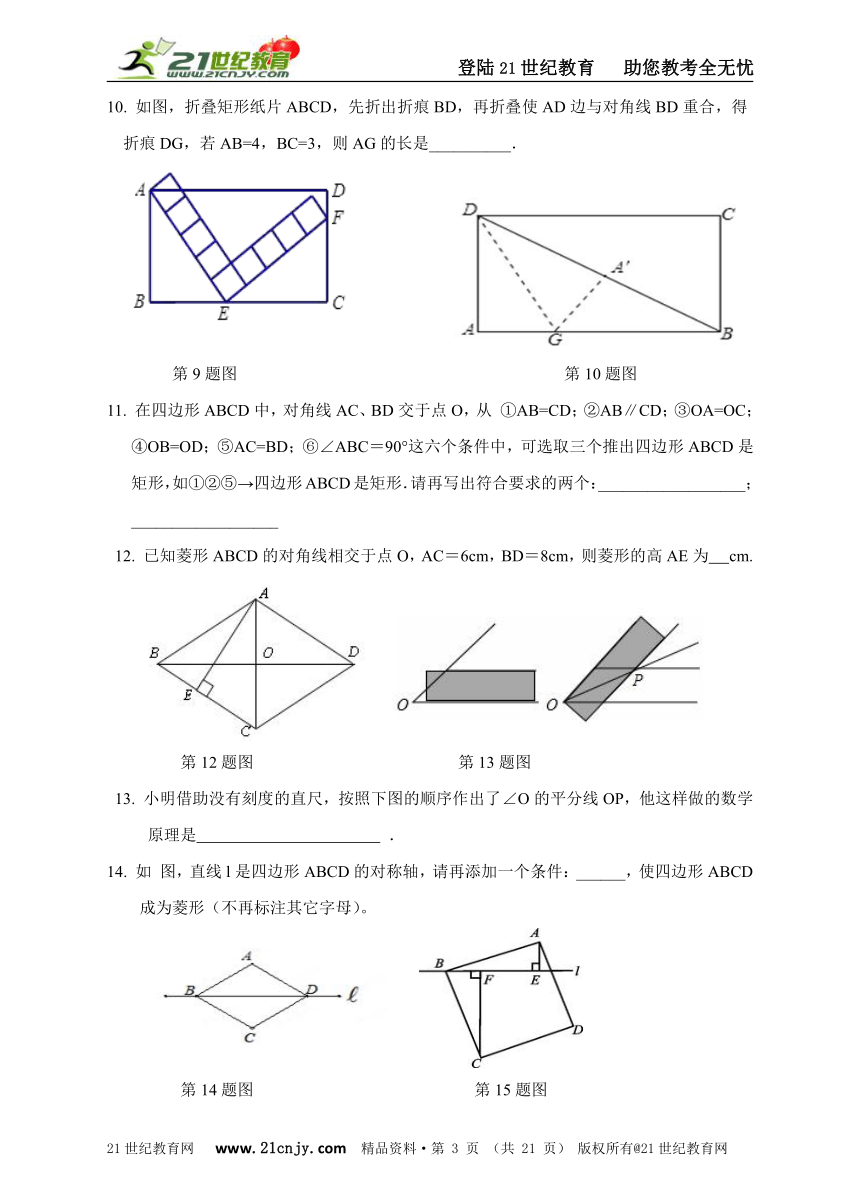
9. 在矩形ABCD中,由9个边长均为1的正方形组成的“L型”模板如图放置,此时量得CF=3,则BC边的长度为_____________.
10. 如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得
折痕DG,若AB=4,BC=3,则AG的长是__________.
第9题图 第10题图
11. 在四边形ABCD中,对角线AC、BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个:__________________;__________________
12. 已知菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,则菱形的高AE为?????cm.
第12题图 第13题图
13. 小明借助没有刻度的直尺,按照下图的顺序作出了∠O的平分线OP,他这样做的数学
原理是????????????????????????????????????????????? .
14. 如 图,直线l是四边形ABCD的对称轴,请再添加一个条件:______,使四边形ABCD
成为菱形(不再标注其它字母)。
21世纪教育网版权所
第14题图 第15题图
15. 如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为???????? .
三、解答题 ?(共7题,75分)
16. (8分)如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD. (1)求证:四边形OCED为菱形; (2)连接AE、BE,AE与BE相等吗?请说明理由.
17. (8分)如图,在平行四边形ABCD中,为上两点,且 ,
. 求证:(1);21世纪教育网版权所 (2)四边形是矩形.
18. (8分)已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别
交AD,BC于E,F两点,连结BE,DF. (1)求证:△DOE≌△BOF. (2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
19.(8分)如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA=3,OB=4.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.
20. (10分)在正方形ABCD外侧作直线AP, 点关于直线AP的对称点为E, 连接BEE,DE , 其中的交直线于点 . (1)依题意补全图1; (2)若 , 求的度数; (3)如图2,若 , 用等式表示线段之间的数量关系,并证明.
??21. (10分)如图,四边形ABCD为矩形,四边形AEDF为菱形. (1)求证:△ABE≌△DCE; (2)试探究:当矩形ABCD边长满足什么关系时,菱形AEDF为正方形?请说明理由.
22. (11分)如图,在Rt△ABC中,∠B=90°,BC=6 , ∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF.
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明现由
(3)当t为何值时,△DEF为直角三角形?请说明理由. 21世纪教育网版权所
23.(12分)如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长 线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG. (1)求证:∠GCF=∠FCE; (2)判断线段PG,PB与DG之间的数量关系,并证明你的结论; (3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存 在,求出BM的长度,若不存在,说明理由.21世纪教育网版权所
答案与解析
1. 答案:A. 解析:试题分析:依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断: A、对角线相等是平行四边形、矩形、菱形、正方形都具有的性质; B、对角线互相垂直是菱形、正方形具有的性质;21世纪教育网版权所 C、对角线相等是矩形和正方形具有的性质; D、对角线互相垂直且相等是正方形具有的性质. 故选A. 考点:平行四边形、矩形、菱形、正方形的性质.
2. 答案:A. 解析:试题分析:∵△ADE绕点E旋转180°得△CFE, ∴AE=CE,DE=EF, ∴四边形ADCF是平行四边形, ∵AC=BC,点D是边AB的中点, ∴∠ADC=90°, ∴四边形ADCF矩形. 故选A. 考点:旋转的性质;矩形的判定.
3. 答案:D. ∴这个菱形的边长是:(cm). ∴这个菱形的周长是13×4=52(cm).21世纪教育网版权所 故选D. 考点:1.菱形的性质;2.勾股定理.
4. 答案:B. 解析:试题分析:由图形作法可知:AD=AB=DC=BC, ∴四边形ABCD是菱形, 故选B. 考点: 1.菱形的判定;2.作图—复杂作图.
5. 答案:B. 解析:试题分析:如图, 设正方形S1的边长为x, ∵△ABC和△CDE都为等腰直角三角形, ∴AB=BC,DE=DC,∠ABC=∠D=90°,21世纪教育网版权所 ∴sin∠CAB=sin45°= , 即AC=BC,同理可得:BC=CE=CD, ∴AC=BC=2CD,又AD=AC+CD=6, ∴CD= , ∴EC2=22+22 , 即EC=2; ∴S1的面积为EC2=2×2=8; ∵∠MAO=∠MOA=45°, ∴AM=MO, ∵MO=MN, ∴AM=MN, ∴M为AN的中点, ∴S2的边长为3, ∴S2的面积为3×3=9, ∴S1+S2=8+9=17. 故选B. 考点:相似三角形的判定与性质.
6. 答案:A 解析:试题分析:作辅助线构造出全等三角形是解题的关键,也是本题的难点.如图:过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD和△OCE全等,根据全等三角形对应边相等可得OE=AD,CE=OD,然后根据点C在第二象限写出坐标即可.∴点C的坐标为 (- , 1)故选A. 考点:1、全等三角形的判定和性质;2、坐标和图形性质;3、正方形的性质.
7. 答案:D 解析:试题分析:如图作CF⊥x轴,BE⊥x轴,F,E分别为垂足,菱形的顶点的坐标为,可得菱形的边长为5,BC∥OA,所以,顶点的纵坐标为4,△OCF≌△EBA,所以得AE=3,OE=8,可得B(8,4) 反比例数的图象经过顶点 , 则的值为32,故选D.21世纪教育网版权所 考点:1.菱形的性质.2.待定系数法求反比例函的解析式.3.勾股定理
8. 答案:B 解析:试题分析:如图,作CE⊥y轴于点E,交双曲线于点G,作DF⊥x轴于点F, 在y=﹣3x+3中,令x=0,解得:y=3,即B的坐标是(0,3)。 令y=0,解得:x=1,即A的坐标是(1,0)。 则OB=3,OA=1。 ∵∠BAD=90°,∴∠BAO+∠DAF=90°。 又∵Rt△ABO中,∠BAO+∠OBA=90°,∴∠FAD=∠OBA。 ∵在△OAB和△FDA中,∠OBA =∠FAD,∠AOB =∠DFA,AB=AD, ∴△OAB≌△FDA(AAS)。 同理,△OAB≌△FDA≌△BEC。 ∴AF=OB=EC=3,DF=OA=BE=1。∴OF=OE=4。 ∴D的坐标是(4,1),代入得:k=4,则函数的解析式是:。 由OE=4得C的纵坐标是4,把y=4代入得:x=1,即G的坐标是(1,4)。 ∴CG=2,即将正方形沿x轴负方向平移2个单位长度后,点C恰好落在该双曲线上。 ∴a=2。故选B
9. 答案:7. 21世纪教育网版权所 解析:试题分析:由图和已知,EF=5,CF=3,∴根据勾股定理可得EC=4. 易证 , ∴BE="CF=3" .∴BC=7. 考点:1.矩形的性质;2.勾股定理;3.全等三角形的判定和性质
10. 答案:??
11. 答案:①②⑥→四边形ABCD是矩形,③④⑤→四边形ABCD是矩形, ③④⑥→四边形AB(如是矩形(任选其中两个皆可);
12. 答案:4.8. 解析:试题分析:由四边形ABCD是菱形,AC=6cm,BD=8cm,即可得AC⊥BD,OC=AC=3cm,OB=BD=4cm,然后由勾股定理求得BC的长,又由S菱形ABCD=AC?BD=BC?AE,即可求得答案. ∵四边形ABCD是菱形,AC=6cm,BD=8cm, ∴AC⊥BD,OC=AC=3cm,OB=BD=4cm, ∴(cm), ∵S菱形ABCD=AC?BD=BC?AE, ∴×6×8=5×AE, ∴AE=4.8(cm). 考点:菱形的性质.
13. 答案:菱形的每一条对角线平分一组对角. 解析:试题分析:按照图的顺序知,四边形AOBP是菱形,然后根据菱形的每一条对角线都平分它的一组对角,得出OP平分∠AOB: 如图,∵直尺的对边互相平行, ∴AP∥OB,OA∥BP. ∴四边形AOBP是平行四边形. ∵直尺的宽度相同,∴AP与OB间的距离=OA与BP间的距离. ∵AOBP的面积不变,∴OA="OB." ∴AOBP是菱形. ∴OP平分∠AOB. 考点:1.作图;2.菱形的判定与性质.
14. 答案:BC=CD不唯一 解析:试题考查知识点:菱形的判定 思路分析: 由直线l是四边形ABCD的对称轴可知,AB=BC,AD=DC,,根据菱形的判定方法,只要四条边都相等即可判定。所以只要AB、BC中的其一与AD、DC中的其一相等即可。 具体解答过程: ∵直线l是四边形ABCD的对称轴 ∴AB=BC,AD=DC, 根据菱形的判定方法,只要四条边都相等即可判定。只要AB、BC中的其一与AD、DC中的其一相等即可。要使AB、BC中的其一与AD、DC中的其一相等,只需:AB=AD、AB=DC、BC=AD、BC=DC、其中任一个满足即可。 试题点评:开放性试题是近年来的热门题型,一般来说,相对都比较简单,但它所包含的思想却很深远
15. 答案: . 解析:试题分析:∵四边形ABCD是正方形, ∴∠CBF+∠FBA=90°,∠CBF+∠BCF=90°, ∴∠BCF=∠ABE, ∵∠AEB=∠BFC=90°,AB=BC, ∴△ABE≌△BCF(AAS) ∴AE=BF,BE=CF, ∴AB= . 故答案是 . 考点:1.正方形的性质2.全等三角形的判定与性质3.勾股定理.
16. 答案:(1)证明见解析;(2)AE=BE,理由见解析. 解析:试题分析:(1)先判断四边形OCDE是平行四边形,又因为四边形ABCD是矩形,两个结论联合起来,可知四边形OCDE是菱形; (2)先证出∠ADE=∠BCE,再证明△ADE≌△BCE,从而得出AE=BE. 试题解析:(1)四边形OCDE是菱形.理由如下: ∵DE∥AC,CE∥BD, ∴四边形OCDE是平行四边形, ∵矩形ABCD的对角线AC、BD相交于点O, ∴OC=AC=BD=OD, ∴四边形OCDE是菱形; (2)AE=BE,理由是: ∵四边形ABCD是矩形, ∴AD=BC,∠ADC=∠BCD, ∵四边形OCDE是菱形, ∴ED=EC,∠EDC=∠ECD, ∴∠EDC+∠ADC =∠ECD+∠BCD, 即:∠ADE =∠BCE 在△ADE和△BCE中, ∵ , ∴△ADE≌△BCE, ∴AE=BE. 考点:1.矩形的性质2.全等三角形的判定与性质3.菱形的判定.
17. 答案:证明见解析. 解析:试题分析:(1)根据题中的已知条件我们不难得出:AB=CD,AF=DE,又因为BE=CF,那么两边都加上EF后,BF=CE,因此就构成了全等三角形的判定中边边边(SSS)的条件. (2)由于四边形ABCD是平行四边形,只要证明其中一角为直角即可. 试题解析:(1)∵BE=CF,BF=BE+EF,CE=CF+EF, ∴BF=CE. ∵四边形ABCD是平行四边形, ∴AB=DC. 在△ABF和△DCE中, , ∴△ABF≌△DCE(SSS). (2)∵△ABF≌△DCE, ∴∠B=∠C. ∵四边形ABCD是平行四边形, ∴AB∥CD. ∴∠B+∠C=180°. ∴∠B=∠C=90°. ∴四边形ABCD是矩形. 考点:1.矩形的判定2.全等三角形的判定与性质3.平行四边形的性质.
18. 答案:(1)证明见解析;(2)当∠DOE=90°时,四边形BFDE为菱形,理由见解析. 解析:试题分析:(1)由四边形ABCD是平行四边形,即可得AD∥BC,OB=OD,从而∠EDO=∠FBO,∠OED=∠OFB,由AAS可证得△DOE≌△BOF. (2)由△DOE≌△BOF,可得DE=BF,即可证得四边形BEDF是平行四边形,又由∠DOE=90°可得EF⊥BD,即可证得四边形BEDF是菱形. 试题解析:(1)∵四边形ABCD是平行四边形,∴AD∥BC,OB=OD, ∴∠EDO=∠FBO,∠OED=∠OFB. ∴△DOE≌△BOF(AAS). (2)当∠DOE=90°时,四边形BFDE为菱形,理由如下: ∵△DOE≌△BOF,∴DE=BF. 又∵ED∥BF,∴四边形BEDF是平行四边形. ∵∠DOE=90°,∴EF⊥BD. ∴BEDF是菱形. 考点:1.平行四边形的判定和性质;2.全等三角形的判定和性质;3.菱形的判定
19. 答案:(1);(2)(3,5)或(3,). 解析:试题分析:(1)首先由OA、OB的长度,即求得A、B的坐标,利用待定系数法即可求解. (2)分P在B点的上边和在B的下边两种情况进行讨论,求得Q的坐标. 试题解析:(1)∵OA=3,OB=4 ∴点A的坐标为(3,0),点B的坐标为(0,4). ∵设直线AB的函数表达式为y=kx+b(k≠0) ∴ , 解得. ∴直线AB的函数表达式为. (2)当P在B的下边时,AB是菱形的对角线,AB的中点D坐标是 , 设过D的与直线AB垂直的直线的解析式是 , 则 , 解得:. ∴P的坐标是. 设Q的坐标是(x,y),则 , 解得:x=3,y=. ∴Q点的坐标是:(3,). 当P在B点的上方时, , ∴AQ="5." ∴Q点的坐标是(3,5). 综上所述,Q点的坐标是(3,5)或(3,). 考点:1.一次函数综合题;2.待定系数法的应用;3.直线上点的坐标与议程的关系;4菱形的性质;5.分类思想的应用.
20. 答案:(1)见解析图形 ∠ADF=25° EF2+FD2=2AB2???证明见解析 解析:试题分析:(1)按照题意补全图形 应用轴对称的性质及正方形的性质、等腰三角形的性质解决问题 依照题意画出图形,然后应用轴对称的性质等进行解答 试题解析:(1)补全图形如图所示: (2) 连接AE 则∠PAB=∠PAE=20°,AE=AB=AD ∵ABCD是正方形 ∴∠BAD=90° ∴∠EAD=130° ∴∠ADF=25° (3) 连接AE、BF、BD 由轴对称的性质可得:EF=BF,AE=AB=AD,∠ABF=∠AEF=∠ADF ∴∠BFD=∠BAD=90° ∴BF2+FD2=BD2 ∴EF2+FD2=2AB2? 考点:1、轴对称的性质;2、正方形的性质;3、勾股定理
21. 答案:(1)证明见解析;(2)当BC=2AB时,菱形AEDF为正方形.理由见解析. 解析:试题分析:(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,根据菱形的四条边都相等可得AE=DE,然后利用“HL”证明Rt△ABE和Rt△DCE全等即可; (2)BC=2AB时,菱形AEDF为正方形.根据全等三角形对应边相等可得BE=CE,然后求出AB=BE,从而求出∠BAE=∠AEB=45°,同理可得∠DEC=45°,然后求出∠AED=90°,最后根据有一个角是90°的菱形是正方形判断. (1)证明:∵四边形ABCD为矩形, ∴∠B=∠C=90°,AB=DC, ∵四边形AEDF为菱形, ∴AE=DE, 在Rt△ABE和Rt△DCE中, , ∴Rt△ABE≌Rt△DCE(HL); (2)解:当BC=2AB时,菱形AEDF为正方形. 理由:∵Rt△ABE≌Rt△DCE, ∴BE=CE,∠AEB=∠DEC, 又∵BC=2AB, ∴AB=BE, ∴∠BAE=∠AEB=45°, 同理可得,∠DEC=45°, ∵∠AEB+∠AED+∠DEC=180°, ∴∠AED=180°-∠AEB-∠DEC=90°, ∴菱形AEDF是正方形. 考点:1.矩形的性质;2.菱形的性质;3.正方形的判定;4. 全等三角形的判定与性质.
22. 答案:(1)因为DF=t又∵AE=t得AE="DF" ? (2)当t=4时,四边形AEFD为菱形 (3)当t=3或时,△DEF为直角三角形 解析:试题分析:(1)在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴DF="t." 又∵AE=t,∴AE="DF" (2)能.理由如下: ∵AB⊥BC,DF⊥BC,∴AE∥DF. 又AE=DF,∴四边形AEFD为平行四边形. ∵∠B=90°,∠C=30°,∴AC=2AB,AB2+BC2=AC2=4AB2 , ∵BC=6 , ∴AB=6,AC=12,∴AD=AC-DC=12-2 t 若使平行四边形AEFD为菱形,则需AE=AD, ∴t=12-2t,解得t=4,即当t=4时,四边形AEFD为菱形 (3)①∠EDF=90°时,四边形EBFD为矩形. 在Rt△AED中,∠ADE=∠C=30°,∴AD=2AE,即12-2t=2t,t=3 ②∠DEF=90°时,由(2)知EF∥AD,∴∠ADE=∠DEF=90°. ∵∠A=90°-∠C=60°,∠AED=30o , ∴AD=AE. 即12-2t=t,∴t= ③∠EFD=90°时,此种情况不存在. 综上所述,当t=3或时,△DEF为直角三角形。 考点:菱形,直角三角形 点评:本题考查菱形,直角三角形,解答本题需要考生掌握菱形的判定方法,会证明一个四边形是菱形,以及直角三角形的判定方法
23. 答案:(1)证明见解析;(2)PG=PB+DG,证明见解析;(3)存在.3;理由见解析. 解析:试题分析::(1)过点F作FH⊥BE于点H,利用正方形的性质,证得△BAP≌△HPF得出PH=AB,BP=FH进一步得出BP+PC=PC+CH,CH=BP=FH,∠FHC=90°,求得∠DCF=90°-45°=45°得出结论; (2)延长PB至K,使BK=DG,连接AK,证得△ABK≌△ADG和△KAP≌△GAP,找出边相等得出结论;?? (3)首先判定存在,在直线AB上取一点M,使四边形DMPF是平行四边形,证得△ABP≌△DAM,进一步球的结论即可. (1)证明:过点F作FH⊥BE于点H, ∵四边形ABCD是正方形, ∴∠ABC=∠PHF=∠DCB=90o,AB=BC, ∴∠BAP+∠APB=90o ∵AP⊥PF, ∴∠APB+∠FPH=90o ∴∠FPH=∠BAP 又∵AP=PF ∴△BAP≌△HPF ∴PH=AB,BP=FH? ∴PH="BC" ∴BP+PC=PC+CH ∴CH="BP=FH" 而∠FHC=90o. ∴∠FCH=CFH=45o ∴∠DCF=90o-45o=45o ∴∠GCF=∠FCE (2)PG=PB+DG 证明:延长PB至K,使BK=DG, ∵四边形ABCD是正方形 ∴AB="AD," ∠ABK=ADG=90o ∴△ABK≌△ADG ∴AK="AG," ∠KAB=∠GAD, 而∠APF="90" o,AP=PF ∴∠PAF=∠PFA="45" o ∴∠BAP+∠KAB=∠KAP="45" o=∠PAF ∴△KAP≌△GAP ∴KP=PG, ∴KB+BP=DG+BP=PG 即,PG=PB+DG (3)存在. 如图,在直线AB上取一点M,使四边形DMPF是平行四边形, 则MD∥PF,且MD=FP, 又∵PF=AP, ∴MD=AP ∵四边形ABCD是正方形 , ∴AB=AD,∠ABP=∠DAM ∴△ABP≌△DAM? ∴AM=BP=2, ∴BM=AB-AM=5-2="3." ∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形. 考点:1.正方形的性质;2.全等三角形的判定与性质;3.平行四边形的判定.
21世纪教育网版权所
一、单选题 ?(每题3分,共8题24分)21世纪教育网版权所
1. 平行四边形、矩形、菱形、正方形都具有的是(??)
A.对角线互相平分
B.对角线互相垂直21世纪教育网版权所
C.对角线相等
D.对角线互相垂直且相等
2. 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是() A.矩形?????? B.菱形?????? C.正方形?????? D.梯形
第2 题图 第4题图
3. 若菱形两条对角线的长分别为10cm和24cm,则这个菱形的周长为(???)
A.13cm
B.26cm
C.34cm
D.52cm
4. 用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是 (?)
A.一组邻边相等的四边形是菱形
B.四边相等的四边形是菱形21世纪教育网版权所
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
5. 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为 , 则的值为
A.16
B.17
C.18
D.19
第5题图 第6题图
6. 如图,将正方形放在平面直角坐标系中,是原点,的坐标为(1,),
点的坐标为(???)
A.(- , 1)
B.(-1,)
C.( , 1)
D.(- , -1)
7. 如图,菱形OABC的顶点C的坐标为(3,4), 顶点A在x轴的正半轴上.反比例函数
的图象经过顶点B, 则k的值为( ????)?21世纪教育网版权所
A.12
B.20
C.24
D.32
第7题图 第8题图
8. 如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是 A.1?????? B.2?????? C.3?????? D.4
二、填空题 ?(每题3分,共7题21分)
9. 在矩形ABCD中,由9个边长均为1的正方形组成的“L型”模板如图放置,此时量得CF=3,则BC边的长度为_____________.
10. 如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得
折痕DG,若AB=4,BC=3,则AG的长是__________.
第9题图 第10题图
11. 在四边形ABCD中,对角线AC、BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个:__________________;__________________
12. 已知菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,则菱形的高AE为?????cm.
第12题图 第13题图
13. 小明借助没有刻度的直尺,按照下图的顺序作出了∠O的平分线OP,他这样做的数学
原理是????????????????????????????????????????????? .
14. 如 图,直线l是四边形ABCD的对称轴,请再添加一个条件:______,使四边形ABCD
成为菱形(不再标注其它字母)。
21世纪教育网版权所
第14题图 第15题图
15. 如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为???????? .
三、解答题 ?(共7题,75分)
16. (8分)如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD. (1)求证:四边形OCED为菱形; (2)连接AE、BE,AE与BE相等吗?请说明理由.
17. (8分)如图,在平行四边形ABCD中,为上两点,且 ,
. 求证:(1);21世纪教育网版权所 (2)四边形是矩形.
18. (8分)已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别
交AD,BC于E,F两点,连结BE,DF. (1)求证:△DOE≌△BOF. (2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
19.(8分)如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA=3,OB=4.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.
20. (10分)在正方形ABCD外侧作直线AP, 点关于直线AP的对称点为E, 连接BEE,DE , 其中的交直线于点 . (1)依题意补全图1; (2)若 , 求的度数; (3)如图2,若 , 用等式表示线段之间的数量关系,并证明.
??21. (10分)如图,四边形ABCD为矩形,四边形AEDF为菱形. (1)求证:△ABE≌△DCE; (2)试探究:当矩形ABCD边长满足什么关系时,菱形AEDF为正方形?请说明理由.
22. (11分)如图,在Rt△ABC中,∠B=90°,BC=6 , ∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF.
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明现由
(3)当t为何值时,△DEF为直角三角形?请说明理由. 21世纪教育网版权所
23.(12分)如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长 线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG. (1)求证:∠GCF=∠FCE; (2)判断线段PG,PB与DG之间的数量关系,并证明你的结论; (3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存 在,求出BM的长度,若不存在,说明理由.21世纪教育网版权所
答案与解析
1. 答案:A. 解析:试题分析:依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断: A、对角线相等是平行四边形、矩形、菱形、正方形都具有的性质; B、对角线互相垂直是菱形、正方形具有的性质;21世纪教育网版权所 C、对角线相等是矩形和正方形具有的性质; D、对角线互相垂直且相等是正方形具有的性质. 故选A. 考点:平行四边形、矩形、菱形、正方形的性质.
2. 答案:A. 解析:试题分析:∵△ADE绕点E旋转180°得△CFE, ∴AE=CE,DE=EF, ∴四边形ADCF是平行四边形, ∵AC=BC,点D是边AB的中点, ∴∠ADC=90°, ∴四边形ADCF矩形. 故选A. 考点:旋转的性质;矩形的判定.
3. 答案:D. ∴这个菱形的边长是:(cm). ∴这个菱形的周长是13×4=52(cm).21世纪教育网版权所 故选D. 考点:1.菱形的性质;2.勾股定理.
4. 答案:B. 解析:试题分析:由图形作法可知:AD=AB=DC=BC, ∴四边形ABCD是菱形, 故选B. 考点: 1.菱形的判定;2.作图—复杂作图.
5. 答案:B. 解析:试题分析:如图, 设正方形S1的边长为x, ∵△ABC和△CDE都为等腰直角三角形, ∴AB=BC,DE=DC,∠ABC=∠D=90°,21世纪教育网版权所 ∴sin∠CAB=sin45°= , 即AC=BC,同理可得:BC=CE=CD, ∴AC=BC=2CD,又AD=AC+CD=6, ∴CD= , ∴EC2=22+22 , 即EC=2; ∴S1的面积为EC2=2×2=8; ∵∠MAO=∠MOA=45°, ∴AM=MO, ∵MO=MN, ∴AM=MN, ∴M为AN的中点, ∴S2的边长为3, ∴S2的面积为3×3=9, ∴S1+S2=8+9=17. 故选B. 考点:相似三角形的判定与性质.
6. 答案:A 解析:试题分析:作辅助线构造出全等三角形是解题的关键,也是本题的难点.如图:过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD和△OCE全等,根据全等三角形对应边相等可得OE=AD,CE=OD,然后根据点C在第二象限写出坐标即可.∴点C的坐标为 (- , 1)故选A. 考点:1、全等三角形的判定和性质;2、坐标和图形性质;3、正方形的性质.
7. 答案:D 解析:试题分析:如图作CF⊥x轴,BE⊥x轴,F,E分别为垂足,菱形的顶点的坐标为,可得菱形的边长为5,BC∥OA,所以,顶点的纵坐标为4,△OCF≌△EBA,所以得AE=3,OE=8,可得B(8,4) 反比例数的图象经过顶点 , 则的值为32,故选D.21世纪教育网版权所 考点:1.菱形的性质.2.待定系数法求反比例函的解析式.3.勾股定理
8. 答案:B 解析:试题分析:如图,作CE⊥y轴于点E,交双曲线于点G,作DF⊥x轴于点F, 在y=﹣3x+3中,令x=0,解得:y=3,即B的坐标是(0,3)。 令y=0,解得:x=1,即A的坐标是(1,0)。 则OB=3,OA=1。 ∵∠BAD=90°,∴∠BAO+∠DAF=90°。 又∵Rt△ABO中,∠BAO+∠OBA=90°,∴∠FAD=∠OBA。 ∵在△OAB和△FDA中,∠OBA =∠FAD,∠AOB =∠DFA,AB=AD, ∴△OAB≌△FDA(AAS)。 同理,△OAB≌△FDA≌△BEC。 ∴AF=OB=EC=3,DF=OA=BE=1。∴OF=OE=4。 ∴D的坐标是(4,1),代入得:k=4,则函数的解析式是:。 由OE=4得C的纵坐标是4,把y=4代入得:x=1,即G的坐标是(1,4)。 ∴CG=2,即将正方形沿x轴负方向平移2个单位长度后,点C恰好落在该双曲线上。 ∴a=2。故选B
9. 答案:7. 21世纪教育网版权所 解析:试题分析:由图和已知,EF=5,CF=3,∴根据勾股定理可得EC=4. 易证 , ∴BE="CF=3" .∴BC=7. 考点:1.矩形的性质;2.勾股定理;3.全等三角形的判定和性质
10. 答案:??
11. 答案:①②⑥→四边形ABCD是矩形,③④⑤→四边形ABCD是矩形, ③④⑥→四边形AB(如是矩形(任选其中两个皆可);
12. 答案:4.8. 解析:试题分析:由四边形ABCD是菱形,AC=6cm,BD=8cm,即可得AC⊥BD,OC=AC=3cm,OB=BD=4cm,然后由勾股定理求得BC的长,又由S菱形ABCD=AC?BD=BC?AE,即可求得答案. ∵四边形ABCD是菱形,AC=6cm,BD=8cm, ∴AC⊥BD,OC=AC=3cm,OB=BD=4cm, ∴(cm), ∵S菱形ABCD=AC?BD=BC?AE, ∴×6×8=5×AE, ∴AE=4.8(cm). 考点:菱形的性质.
13. 答案:菱形的每一条对角线平分一组对角. 解析:试题分析:按照图的顺序知,四边形AOBP是菱形,然后根据菱形的每一条对角线都平分它的一组对角,得出OP平分∠AOB: 如图,∵直尺的对边互相平行, ∴AP∥OB,OA∥BP. ∴四边形AOBP是平行四边形. ∵直尺的宽度相同,∴AP与OB间的距离=OA与BP间的距离. ∵AOBP的面积不变,∴OA="OB." ∴AOBP是菱形. ∴OP平分∠AOB. 考点:1.作图;2.菱形的判定与性质.
14. 答案:BC=CD不唯一 解析:试题考查知识点:菱形的判定 思路分析: 由直线l是四边形ABCD的对称轴可知,AB=BC,AD=DC,,根据菱形的判定方法,只要四条边都相等即可判定。所以只要AB、BC中的其一与AD、DC中的其一相等即可。 具体解答过程: ∵直线l是四边形ABCD的对称轴 ∴AB=BC,AD=DC, 根据菱形的判定方法,只要四条边都相等即可判定。只要AB、BC中的其一与AD、DC中的其一相等即可。要使AB、BC中的其一与AD、DC中的其一相等,只需:AB=AD、AB=DC、BC=AD、BC=DC、其中任一个满足即可。 试题点评:开放性试题是近年来的热门题型,一般来说,相对都比较简单,但它所包含的思想却很深远
15. 答案: . 解析:试题分析:∵四边形ABCD是正方形, ∴∠CBF+∠FBA=90°,∠CBF+∠BCF=90°, ∴∠BCF=∠ABE, ∵∠AEB=∠BFC=90°,AB=BC, ∴△ABE≌△BCF(AAS) ∴AE=BF,BE=CF, ∴AB= . 故答案是 . 考点:1.正方形的性质2.全等三角形的判定与性质3.勾股定理.
16. 答案:(1)证明见解析;(2)AE=BE,理由见解析. 解析:试题分析:(1)先判断四边形OCDE是平行四边形,又因为四边形ABCD是矩形,两个结论联合起来,可知四边形OCDE是菱形; (2)先证出∠ADE=∠BCE,再证明△ADE≌△BCE,从而得出AE=BE. 试题解析:(1)四边形OCDE是菱形.理由如下: ∵DE∥AC,CE∥BD, ∴四边形OCDE是平行四边形, ∵矩形ABCD的对角线AC、BD相交于点O, ∴OC=AC=BD=OD, ∴四边形OCDE是菱形; (2)AE=BE,理由是: ∵四边形ABCD是矩形, ∴AD=BC,∠ADC=∠BCD, ∵四边形OCDE是菱形, ∴ED=EC,∠EDC=∠ECD, ∴∠EDC+∠ADC =∠ECD+∠BCD, 即:∠ADE =∠BCE 在△ADE和△BCE中, ∵ , ∴△ADE≌△BCE, ∴AE=BE. 考点:1.矩形的性质2.全等三角形的判定与性质3.菱形的判定.
17. 答案:证明见解析. 解析:试题分析:(1)根据题中的已知条件我们不难得出:AB=CD,AF=DE,又因为BE=CF,那么两边都加上EF后,BF=CE,因此就构成了全等三角形的判定中边边边(SSS)的条件. (2)由于四边形ABCD是平行四边形,只要证明其中一角为直角即可. 试题解析:(1)∵BE=CF,BF=BE+EF,CE=CF+EF, ∴BF=CE. ∵四边形ABCD是平行四边形, ∴AB=DC. 在△ABF和△DCE中, , ∴△ABF≌△DCE(SSS). (2)∵△ABF≌△DCE, ∴∠B=∠C. ∵四边形ABCD是平行四边形, ∴AB∥CD. ∴∠B+∠C=180°. ∴∠B=∠C=90°. ∴四边形ABCD是矩形. 考点:1.矩形的判定2.全等三角形的判定与性质3.平行四边形的性质.
18. 答案:(1)证明见解析;(2)当∠DOE=90°时,四边形BFDE为菱形,理由见解析. 解析:试题分析:(1)由四边形ABCD是平行四边形,即可得AD∥BC,OB=OD,从而∠EDO=∠FBO,∠OED=∠OFB,由AAS可证得△DOE≌△BOF. (2)由△DOE≌△BOF,可得DE=BF,即可证得四边形BEDF是平行四边形,又由∠DOE=90°可得EF⊥BD,即可证得四边形BEDF是菱形. 试题解析:(1)∵四边形ABCD是平行四边形,∴AD∥BC,OB=OD, ∴∠EDO=∠FBO,∠OED=∠OFB. ∴△DOE≌△BOF(AAS). (2)当∠DOE=90°时,四边形BFDE为菱形,理由如下: ∵△DOE≌△BOF,∴DE=BF. 又∵ED∥BF,∴四边形BEDF是平行四边形. ∵∠DOE=90°,∴EF⊥BD. ∴BEDF是菱形. 考点:1.平行四边形的判定和性质;2.全等三角形的判定和性质;3.菱形的判定
19. 答案:(1);(2)(3,5)或(3,). 解析:试题分析:(1)首先由OA、OB的长度,即求得A、B的坐标,利用待定系数法即可求解. (2)分P在B点的上边和在B的下边两种情况进行讨论,求得Q的坐标. 试题解析:(1)∵OA=3,OB=4 ∴点A的坐标为(3,0),点B的坐标为(0,4). ∵设直线AB的函数表达式为y=kx+b(k≠0) ∴ , 解得. ∴直线AB的函数表达式为. (2)当P在B的下边时,AB是菱形的对角线,AB的中点D坐标是 , 设过D的与直线AB垂直的直线的解析式是 , 则 , 解得:. ∴P的坐标是. 设Q的坐标是(x,y),则 , 解得:x=3,y=. ∴Q点的坐标是:(3,). 当P在B点的上方时, , ∴AQ="5." ∴Q点的坐标是(3,5). 综上所述,Q点的坐标是(3,5)或(3,). 考点:1.一次函数综合题;2.待定系数法的应用;3.直线上点的坐标与议程的关系;4菱形的性质;5.分类思想的应用.
20. 答案:(1)见解析图形 ∠ADF=25° EF2+FD2=2AB2???证明见解析 解析:试题分析:(1)按照题意补全图形 应用轴对称的性质及正方形的性质、等腰三角形的性质解决问题 依照题意画出图形,然后应用轴对称的性质等进行解答 试题解析:(1)补全图形如图所示: (2) 连接AE 则∠PAB=∠PAE=20°,AE=AB=AD ∵ABCD是正方形 ∴∠BAD=90° ∴∠EAD=130° ∴∠ADF=25° (3) 连接AE、BF、BD 由轴对称的性质可得:EF=BF,AE=AB=AD,∠ABF=∠AEF=∠ADF ∴∠BFD=∠BAD=90° ∴BF2+FD2=BD2 ∴EF2+FD2=2AB2? 考点:1、轴对称的性质;2、正方形的性质;3、勾股定理
21. 答案:(1)证明见解析;(2)当BC=2AB时,菱形AEDF为正方形.理由见解析. 解析:试题分析:(1)根据矩形的性质可得∠B=∠C=90°,AB=DC,根据菱形的四条边都相等可得AE=DE,然后利用“HL”证明Rt△ABE和Rt△DCE全等即可; (2)BC=2AB时,菱形AEDF为正方形.根据全等三角形对应边相等可得BE=CE,然后求出AB=BE,从而求出∠BAE=∠AEB=45°,同理可得∠DEC=45°,然后求出∠AED=90°,最后根据有一个角是90°的菱形是正方形判断. (1)证明:∵四边形ABCD为矩形, ∴∠B=∠C=90°,AB=DC, ∵四边形AEDF为菱形, ∴AE=DE, 在Rt△ABE和Rt△DCE中, , ∴Rt△ABE≌Rt△DCE(HL); (2)解:当BC=2AB时,菱形AEDF为正方形. 理由:∵Rt△ABE≌Rt△DCE, ∴BE=CE,∠AEB=∠DEC, 又∵BC=2AB, ∴AB=BE, ∴∠BAE=∠AEB=45°, 同理可得,∠DEC=45°, ∵∠AEB+∠AED+∠DEC=180°, ∴∠AED=180°-∠AEB-∠DEC=90°, ∴菱形AEDF是正方形. 考点:1.矩形的性质;2.菱形的性质;3.正方形的判定;4. 全等三角形的判定与性质.
22. 答案:(1)因为DF=t又∵AE=t得AE="DF" ? (2)当t=4时,四边形AEFD为菱形 (3)当t=3或时,△DEF为直角三角形 解析:试题分析:(1)在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴DF="t." 又∵AE=t,∴AE="DF" (2)能.理由如下: ∵AB⊥BC,DF⊥BC,∴AE∥DF. 又AE=DF,∴四边形AEFD为平行四边形. ∵∠B=90°,∠C=30°,∴AC=2AB,AB2+BC2=AC2=4AB2 , ∵BC=6 , ∴AB=6,AC=12,∴AD=AC-DC=12-2 t 若使平行四边形AEFD为菱形,则需AE=AD, ∴t=12-2t,解得t=4,即当t=4时,四边形AEFD为菱形 (3)①∠EDF=90°时,四边形EBFD为矩形. 在Rt△AED中,∠ADE=∠C=30°,∴AD=2AE,即12-2t=2t,t=3 ②∠DEF=90°时,由(2)知EF∥AD,∴∠ADE=∠DEF=90°. ∵∠A=90°-∠C=60°,∠AED=30o , ∴AD=AE. 即12-2t=t,∴t= ③∠EFD=90°时,此种情况不存在. 综上所述,当t=3或时,△DEF为直角三角形。 考点:菱形,直角三角形 点评:本题考查菱形,直角三角形,解答本题需要考生掌握菱形的判定方法,会证明一个四边形是菱形,以及直角三角形的判定方法
23. 答案:(1)证明见解析;(2)PG=PB+DG,证明见解析;(3)存在.3;理由见解析. 解析:试题分析::(1)过点F作FH⊥BE于点H,利用正方形的性质,证得△BAP≌△HPF得出PH=AB,BP=FH进一步得出BP+PC=PC+CH,CH=BP=FH,∠FHC=90°,求得∠DCF=90°-45°=45°得出结论; (2)延长PB至K,使BK=DG,连接AK,证得△ABK≌△ADG和△KAP≌△GAP,找出边相等得出结论;?? (3)首先判定存在,在直线AB上取一点M,使四边形DMPF是平行四边形,证得△ABP≌△DAM,进一步球的结论即可. (1)证明:过点F作FH⊥BE于点H, ∵四边形ABCD是正方形, ∴∠ABC=∠PHF=∠DCB=90o,AB=BC, ∴∠BAP+∠APB=90o ∵AP⊥PF, ∴∠APB+∠FPH=90o ∴∠FPH=∠BAP 又∵AP=PF ∴△BAP≌△HPF ∴PH=AB,BP=FH? ∴PH="BC" ∴BP+PC=PC+CH ∴CH="BP=FH" 而∠FHC=90o. ∴∠FCH=CFH=45o ∴∠DCF=90o-45o=45o ∴∠GCF=∠FCE (2)PG=PB+DG 证明:延长PB至K,使BK=DG, ∵四边形ABCD是正方形 ∴AB="AD," ∠ABK=ADG=90o ∴△ABK≌△ADG ∴AK="AG," ∠KAB=∠GAD, 而∠APF="90" o,AP=PF ∴∠PAF=∠PFA="45" o ∴∠BAP+∠KAB=∠KAP="45" o=∠PAF ∴△KAP≌△GAP ∴KP=PG, ∴KB+BP=DG+BP=PG 即,PG=PB+DG (3)存在. 如图,在直线AB上取一点M,使四边形DMPF是平行四边形, 则MD∥PF,且MD=FP, 又∵PF=AP, ∴MD=AP ∵四边形ABCD是正方形 , ∴AB=AD,∠ABP=∠DAM ∴△ABP≌△DAM? ∴AM=BP=2, ∴BM=AB-AM=5-2="3." ∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形. 考点:1.正方形的性质;2.全等三角形的判定与性质;3.平行四边形的判定.
21世纪教育网版权所
