正弦、余弦函数的性质(山东省淄博市张店区)
文档属性
| 名称 | 正弦、余弦函数的性质(山东省淄博市张店区) |  | |
| 格式 | rar | ||
| 文件大小 | 354.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-14 12:33:00 | ||
图片预览

文档简介
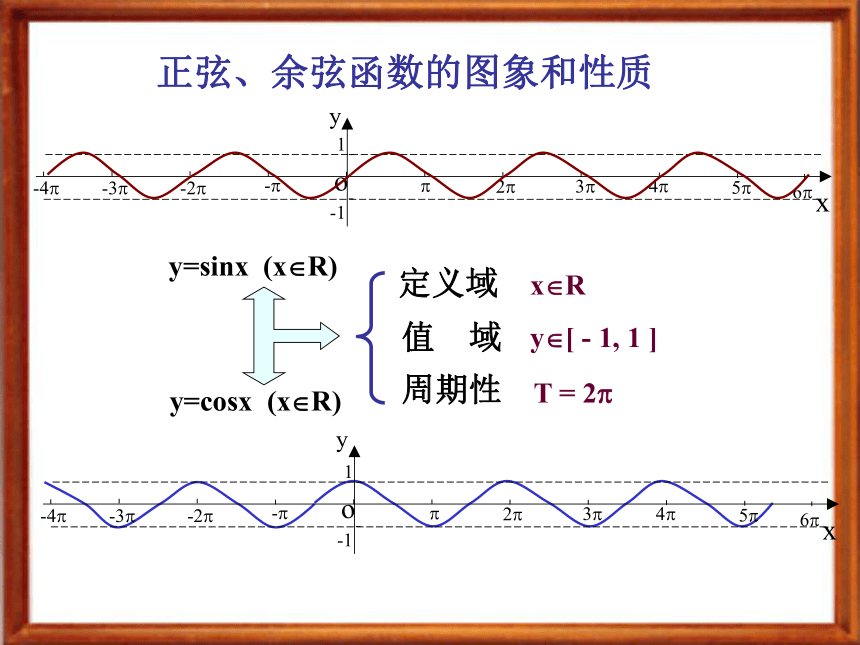
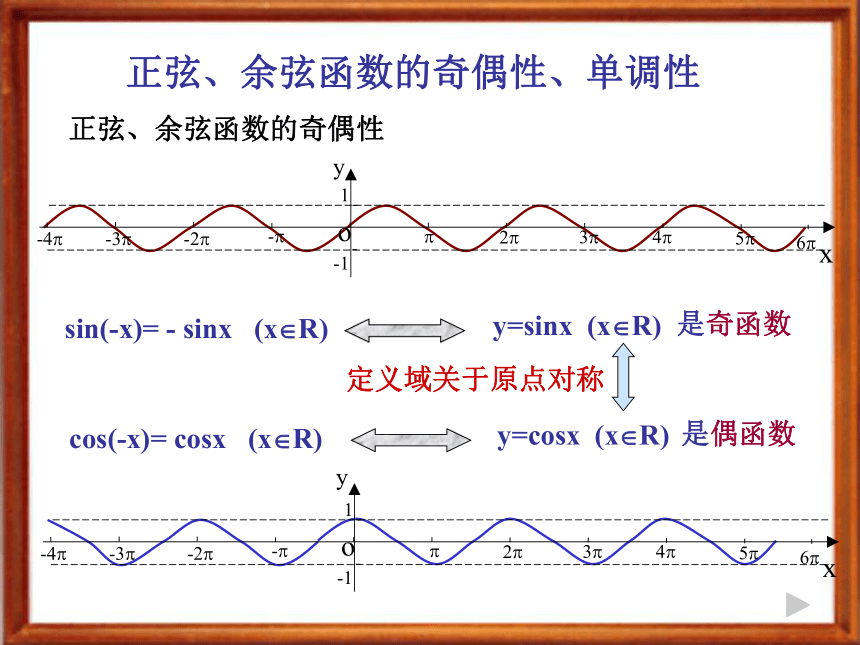
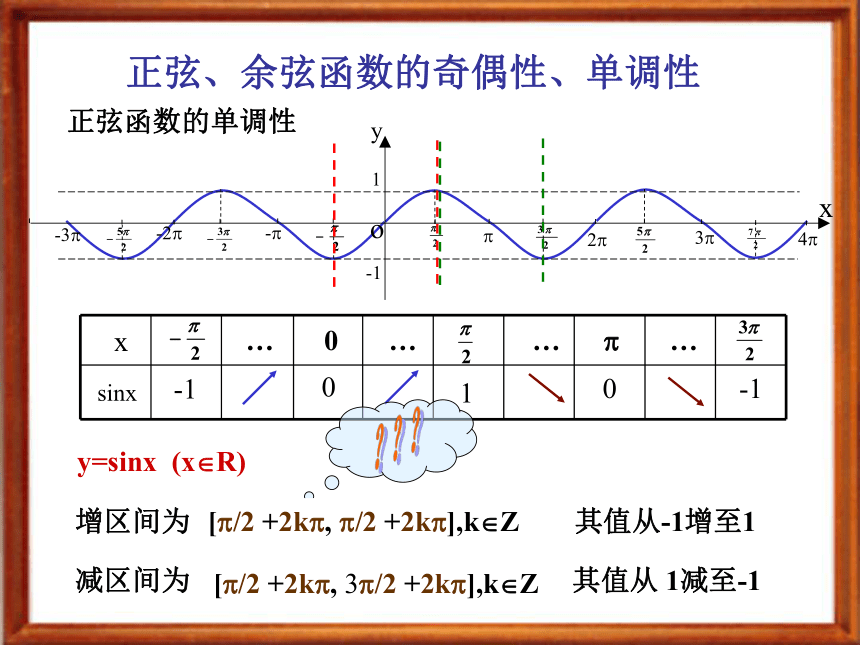
课件8张PPT。 正弦、余弦函数的性质(奇偶性、单调性)主讲人: 冯建仓 正弦、余弦函数的图象和性质 y=sinx (x?R) y=cosx (x?R) 定义域值 域周期性x?Ry?[ - 1, 1 ]T = 2? 正弦、余弦函数的奇偶性、单调性 sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数cos(-x)= cosx (x?R) y=cosx (x?R)是偶函数定义域关于原点对称 正弦、余弦函数的奇偶性 正弦、余弦函数的奇偶性、单调性 正弦函数的单调性 y=sinx (x?R)增区间为 [-?/2 , ?/2 ] 其值从-1增至1-1 0 1 0 -1减区间为 [?/2 ,3 ?/2 ] 其值从 1减至-1[?/2 +2k?, ?/2 +2k?],k?Z[?/2 +2k?, 3?/2 +2k?],k?Z 正弦、余弦函数的奇偶性、单调性 余弦函数的单调性 y=cosx (x?R)-1 0 1 0 -1小 结: 正弦、余弦函数的奇偶性、单调性 奇偶性 单调性(单调区间)奇函数偶函数单调递增单调递减函数求函数的单调区间:1. 直接利用相关性质2. 复合函数的单调性3. 利用图象寻找单调区间 正弦、余弦函数的奇偶性、单调性 y=sinxy=sinx (x?R) 图象关于原点对称
