蒙城六中2008-2009学年第一学期第三次月考数学卷
文档属性
| 名称 | 蒙城六中2008-2009学年第一学期第三次月考数学卷 |  | |
| 格式 | rar | ||
| 文件大小 | 88.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-13 09:34:00 | ||
图片预览

文档简介
蒙城六中2008-2009学年第一学期第三次月考
九年级数学模拟试卷 姓名 分数
一、选择题(每题4分,共40分)
1、抛物线y=x-6x+21的顶点坐标是 ( )
A.(-3,1) B.(-3,-1) C.(6,3) D.(6,1)
2. 一个斜坡的坡角为30°,则这个斜坡的坡度为( )。
A. 1:2 B.:2 C. 1: D. :1
3.已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,则⊙O的半径是( )
A.3厘米 B.4厘米 C.5厘米 D.8厘米
4.下列图形中,是旋转对称图形而不是轴对称图形的是 ( )
5.上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,从A、B两处分别测得小岛M在北偏东45°和北偏东15°方向,则在B处船与小岛M的距离是 ( )
A.20海里 B.20海里 C.15海里 D.20
6.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)<b,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=4,AD=6,OM=x,ON=y则y与x的关系是 ( )
A. B. C. D.
8.如图,某大学的校门是一抛物线水泥建筑物,大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑厚度忽略不计) ( )
A.9.2米 B.9.1米 C.9米 D.5.1米
如图,已知双曲线(x>0)经过矩形OABC边AB的中点E,交BC于点F,且四边形OEBF的面积为,则k=( )
A、2 B、3 C、4、 D、6
10.如图,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任一点,过P作EF∥AC,与平行四边形的两条边分别交于点E,F。设BP=,EF=,则能反映与之间关系的图象为( )
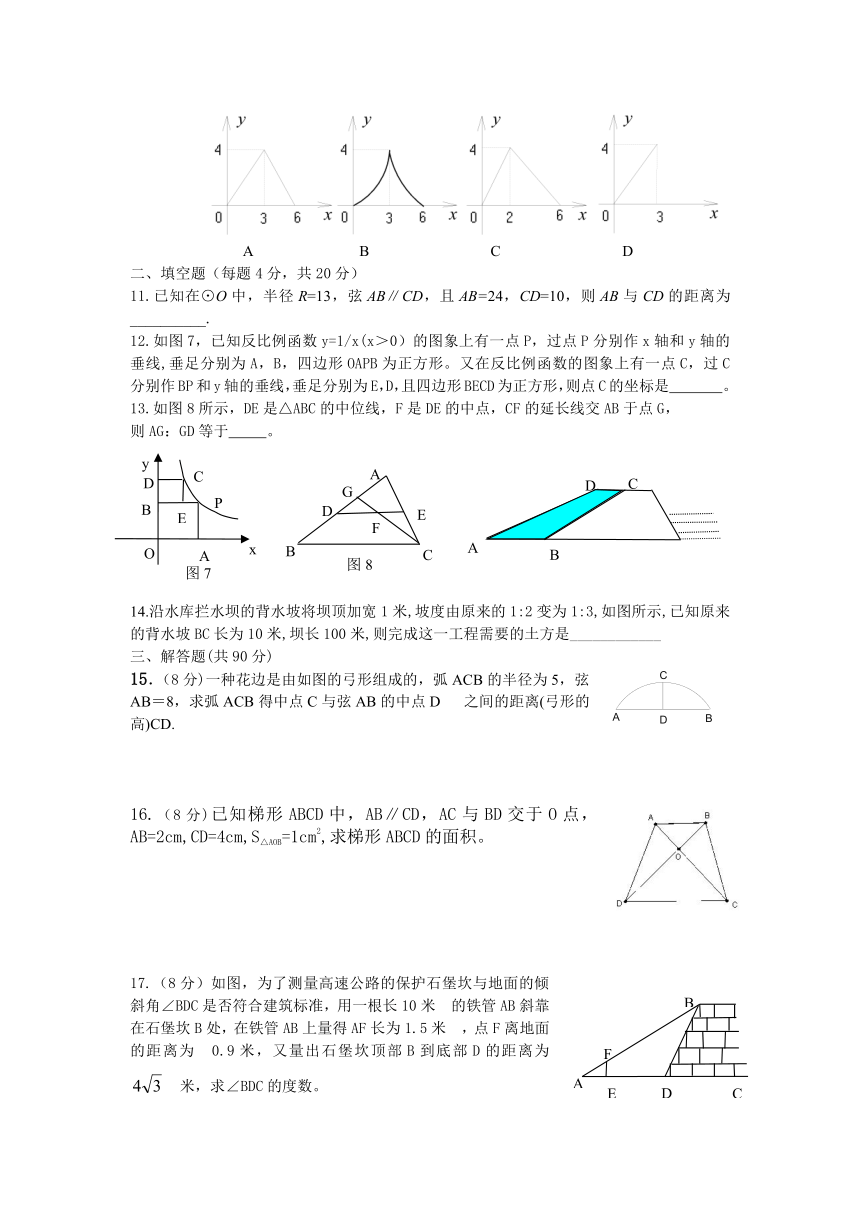
A B C D
二、填空题(每题4分,共20分)
11.已知在⊙O中,半径R=13,弦AB∥CD,且AB=24,CD=10,则AB与CD的距离为__________.
12.如图7,已知反比例函数y=1/x(x>0)的图象上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A,B,四边形OAPB为正方形。又在反比例函数的图象上有一点C,过C分别作BP和y轴的垂线,垂足分别为E,D,且四边形BECD为正方形,则点C的坐标是 。
13.如图8所示,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,
则AG:GD等于 。
14.沿水库拦水坝的背水坡将坝顶加宽1米,坡度由原来的1:2变为1:3,如图所示,已知原来的背水坡BC长为10米,坝长100米,则完成这一工程需要的土方是____________
三、解答题(共90分)
15.(8分)一种花边是由如图的弓形组成的,弧ACB的半径为5,弦AB=8,求弧ACB得中点C与弦AB的中点D 之间的距离(弓形的高)CD. ( http: / / 0712xiaochang.uu1001.com )
16.(8分)已知梯形ABCD中,AB∥CD,AC与BD交于O点,AB=2cm,CD=4cm,S△AOB=1cm2,求梯形ABCD的面积。
17.(8分)如图,为了测量高速公路的保护石堡坎与地面的倾斜角∠BDC是否符合建筑标准,用一根长10米 的铁管AB斜靠在石堡坎B处,在铁管AB上量得AF长为1.5米 ,点F离地面的距离为 0.9米,又量出石堡坎顶部B到底部D的距离为 米,求∠BDC的度数。
18.(8分抛物线y=x2+2x-3与x轴交于A、B两点,与y轴交于C点,顶点为M,
(1)、求M的坐标
(2)、求△AMC的面积。
19.(10分)在Rt△ABC中,∠BAC=90°,AB=AC=1,点D在线段BC上运动(不与B、C重合),DE交AC于E,∠ADE=45°,
求证:△ABD∽△DCE;
当△ADE是等腰三角形时,求AE的长。
20.(10分)如图;点0是∠CAE角平分线AP上一点,以O为圆心作⊙O分别交∠CAE两边于点B,C,D,E;求证:AC=AE
21.(12分)已知:如图,在矩形ABCD中,AB=,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边作等边△PEF,使顶点P在AD上,PE、PF分别交AC于点G、H,
(1)求△PEF的边长;
(2)求证:=;
22.(12分)矩形ABOD的顶点A是函数与函数在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,矩形ABOD的面积为3,
(1)求两函数的解析式(2)求两函数的交点A,C的坐标。
(3)若点P是x轴上的一动点,三角形APC的面积为5,求点P的坐标。
23.(14分)如图,在平面直角坐标系中,矩形的顶点的坐标为(4,0),顶点的坐标为(0,2),将矩形绕点逆时针旋转,使落在轴的点处,得到矩形,与交于点。
(1)判断△和△是否相似,并说明理由;
(2)求过点的反比例函数的解析式;
(3)设(2)中的反比例函数图像交于点,求直线的解析式;
(4)请探索:求出的反比例函数的图像是否经过矩形的对称中心,并说明理由。
参考答案
选择题 CCCBB CDBBA
填空题 ⑾17或7 ⑿ ( )⒀ 2:1 ⒁ ()立方米
⒂2 ⒃9cm2 ⒄ 600 ⒅ M(-1,-4) 3
⒆ ⑴ 略⑵2-或
⒇作OM⊥BC于M ON⊥DE于N;则OM=ON,BC=DE.易证,从而有AM=AN.又,所以MC=NE ,所以AC=AE
(21) ⑴ 2 ⑵在Rt中∵∴ ∵ ∴∴∴ ∴ 即 =;
(22)(1)y=- y=-x+2 (2)A(-1,3) C(3,-1) (3)(4.5,0)或(-0.5,0)
(23)(1)略 (2)y= (3)y=- (4)经过
C
B
G
A
D
F
E
A
B
P
C
D
E
x
y
O
图7
图8
B
A
D
C
C
A
D
F
B
E
B
C
A
D
F
P
E
G
H
A
B
D
O
x
y
C
F
G
E
B
A
P
N
M
O
x
y
九年级数学模拟试卷 姓名 分数
一、选择题(每题4分,共40分)
1、抛物线y=x-6x+21的顶点坐标是 ( )
A.(-3,1) B.(-3,-1) C.(6,3) D.(6,1)
2. 一个斜坡的坡角为30°,则这个斜坡的坡度为( )。
A. 1:2 B.:2 C. 1: D. :1
3.已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,则⊙O的半径是( )
A.3厘米 B.4厘米 C.5厘米 D.8厘米
4.下列图形中,是旋转对称图形而不是轴对称图形的是 ( )
5.上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处,从A、B两处分别测得小岛M在北偏东45°和北偏东15°方向,则在B处船与小岛M的距离是 ( )
A.20海里 B.20海里 C.15海里 D.20
6.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)<b,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=4,AD=6,OM=x,ON=y则y与x的关系是 ( )
A. B. C. D.
8.如图,某大学的校门是一抛物线水泥建筑物,大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑厚度忽略不计) ( )
A.9.2米 B.9.1米 C.9米 D.5.1米
如图,已知双曲线(x>0)经过矩形OABC边AB的中点E,交BC于点F,且四边形OEBF的面积为,则k=( )
A、2 B、3 C、4、 D、6
10.如图,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任一点,过P作EF∥AC,与平行四边形的两条边分别交于点E,F。设BP=,EF=,则能反映与之间关系的图象为( )
A B C D
二、填空题(每题4分,共20分)
11.已知在⊙O中,半径R=13,弦AB∥CD,且AB=24,CD=10,则AB与CD的距离为__________.
12.如图7,已知反比例函数y=1/x(x>0)的图象上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A,B,四边形OAPB为正方形。又在反比例函数的图象上有一点C,过C分别作BP和y轴的垂线,垂足分别为E,D,且四边形BECD为正方形,则点C的坐标是 。
13.如图8所示,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,
则AG:GD等于 。
14.沿水库拦水坝的背水坡将坝顶加宽1米,坡度由原来的1:2变为1:3,如图所示,已知原来的背水坡BC长为10米,坝长100米,则完成这一工程需要的土方是____________
三、解答题(共90分)
15.(8分)一种花边是由如图的弓形组成的,弧ACB的半径为5,弦AB=8,求弧ACB得中点C与弦AB的中点D 之间的距离(弓形的高)CD. ( http: / / 0712xiaochang.uu1001.com )
16.(8分)已知梯形ABCD中,AB∥CD,AC与BD交于O点,AB=2cm,CD=4cm,S△AOB=1cm2,求梯形ABCD的面积。
17.(8分)如图,为了测量高速公路的保护石堡坎与地面的倾斜角∠BDC是否符合建筑标准,用一根长10米 的铁管AB斜靠在石堡坎B处,在铁管AB上量得AF长为1.5米 ,点F离地面的距离为 0.9米,又量出石堡坎顶部B到底部D的距离为 米,求∠BDC的度数。
18.(8分抛物线y=x2+2x-3与x轴交于A、B两点,与y轴交于C点,顶点为M,
(1)、求M的坐标
(2)、求△AMC的面积。
19.(10分)在Rt△ABC中,∠BAC=90°,AB=AC=1,点D在线段BC上运动(不与B、C重合),DE交AC于E,∠ADE=45°,
求证:△ABD∽△DCE;
当△ADE是等腰三角形时,求AE的长。
20.(10分)如图;点0是∠CAE角平分线AP上一点,以O为圆心作⊙O分别交∠CAE两边于点B,C,D,E;求证:AC=AE
21.(12分)已知:如图,在矩形ABCD中,AB=,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边作等边△PEF,使顶点P在AD上,PE、PF分别交AC于点G、H,
(1)求△PEF的边长;
(2)求证:=;
22.(12分)矩形ABOD的顶点A是函数与函数在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,矩形ABOD的面积为3,
(1)求两函数的解析式(2)求两函数的交点A,C的坐标。
(3)若点P是x轴上的一动点,三角形APC的面积为5,求点P的坐标。
23.(14分)如图,在平面直角坐标系中,矩形的顶点的坐标为(4,0),顶点的坐标为(0,2),将矩形绕点逆时针旋转,使落在轴的点处,得到矩形,与交于点。
(1)判断△和△是否相似,并说明理由;
(2)求过点的反比例函数的解析式;
(3)设(2)中的反比例函数图像交于点,求直线的解析式;
(4)请探索:求出的反比例函数的图像是否经过矩形的对称中心,并说明理由。
参考答案
选择题 CCCBB CDBBA
填空题 ⑾17或7 ⑿ ( )⒀ 2:1 ⒁ ()立方米
⒂2 ⒃9cm2 ⒄ 600 ⒅ M(-1,-4) 3
⒆ ⑴ 略⑵2-或
⒇作OM⊥BC于M ON⊥DE于N;则OM=ON,BC=DE.易证,从而有AM=AN.又,所以MC=NE ,所以AC=AE
(21) ⑴ 2 ⑵在Rt中∵∴ ∵ ∴∴∴ ∴ 即 =;
(22)(1)y=- y=-x+2 (2)A(-1,3) C(3,-1) (3)(4.5,0)或(-0.5,0)
(23)(1)略 (2)y= (3)y=- (4)经过
C
B
G
A
D
F
E
A
B
P
C
D
E
x
y
O
图7
图8
B
A
D
C
C
A
D
F
B
E
B
C
A
D
F
P
E
G
H
A
B
D
O
x
y
C
F
G
E
B
A
P
N
M
O
x
y
同课章节目录
